Skip to main content
LibreTexts - Ukrayinska

1.11: Конгруентні кути та бісектриси кута

  1. Last updated
  2. Save as PDF
  • Page ID
    54946

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Кути тієї ж міри, і лінії або частини ліній, які ділять кути на дві рівні половини.

    Коли дві геометричні фігури мають однакову форму та розмір (або однакову міру кута у випадку кутів), вони, як кажуть, є конгруентними.

    Позначте це Скажи це
    \(\angle ABC \cong \angle DEF\) \(ABC\)Кут конгруентний куту\(DEF\).

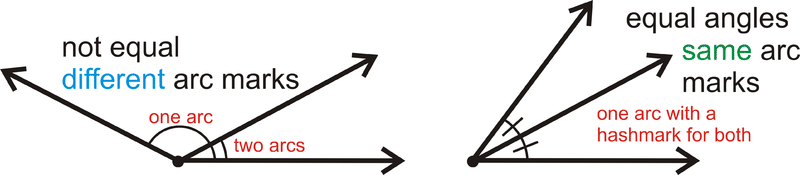
    Якщо два кути конгруентні, то вони теж рівні. Для маркування рівних кутів використовуємо розмітку кута, як показано нижче:

    F-D_0ad 66АБ 247A01 ДБ0015Б87Е2 АФ 1761БФ 3438Б1Б7Ф271A291311A2A2+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{1}\)

    Бісектриса кута - це лінія, або частина лінії, яка ділить кут на два конгруентні кути, кожен з яких має міру рівно половину початкового кута. Кожен кут має рівно одну бісектрису кута.

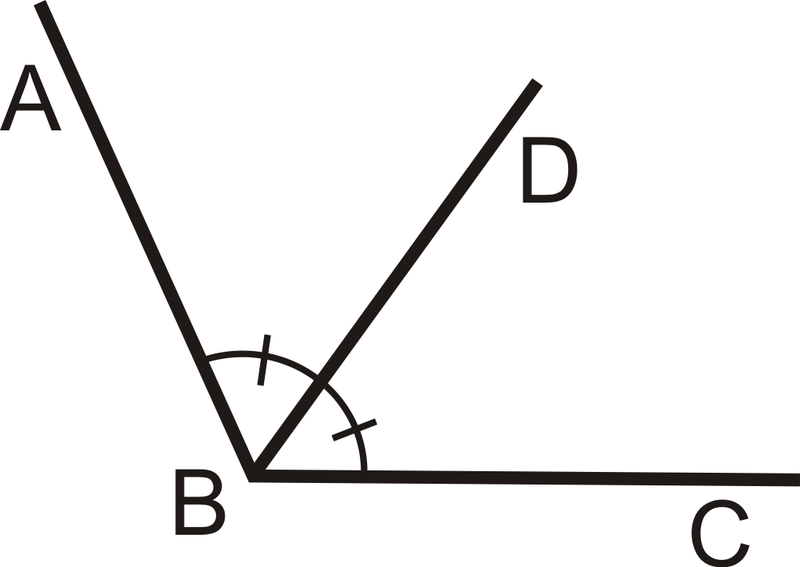
    F-D_27AFF5AED 43257 CDFB68E395883C4161 бути 98 дед C7C8DC91A8E88E+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{2}\)

    На малюнку вище,\(\overline{BD}\) це кут бісектриси\(\angle ABC\), так\(\angle ABC \cong \angle DBC\) і\(m \angle ABD \cong \dfrac{1}{2} m \angle ABC\).

    Що робити, якщо вам сказали, що відрізок лінії ділить кут навпіл? Як би ви знайшли міри двох нових кутів, утворених цим сегментом?

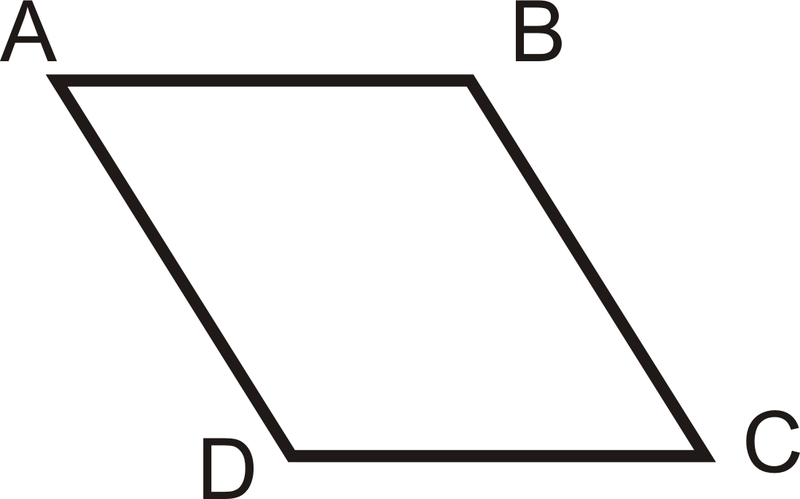
    Для прикладів 1 і 2 скопіюйте малюнок нижче та позначте його наступною інформацією:

    F-D_9A867539E404BBA62DA8 АФ 4Е566Ф7Б4Ф90А209239Ф13Б447100 ЕЕДА+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{3}\)

    Приклад\(\PageIndex{1}\)

    \(\angle A \cong \angle C\)

    Рішення

    У вас повинна бути відповідна маркування на\(\angle A\) і\(\angle C\).

    Приклад\(\PageIndex{2}\)

    \(\angle B \cong \angle D\)

    Рішення

    Ви повинні мати відповідне маркування на\(\angle B\) і\(\angle D\) (які відрізняються від маркування, яку ви зробили в прикладі 1).

    Приклад\(\PageIndex{3}\)

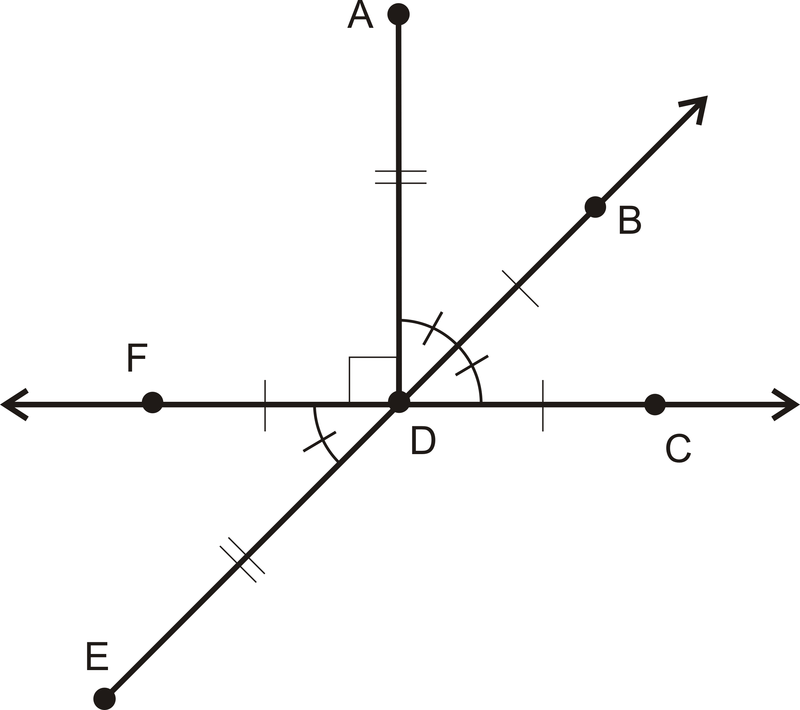
    Запишіть всі оператори рівного кута.

    F-д_9а 6700Е4Е1Д8Ф7С4722А6БФ 4668А0Б40КБ5ФБ6Б6БД46С24Б8Б8А1Е71Д+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)

    Рішення

    \(m \angle ADB=m\angle BDC=m \angle FDE=45^{\circ}\)

    \(m \angle ADF=m\angle ADC=90^{\circ}\)

    Приклад\(\PageIndex{4}\)

    Яка міра кожного кута?

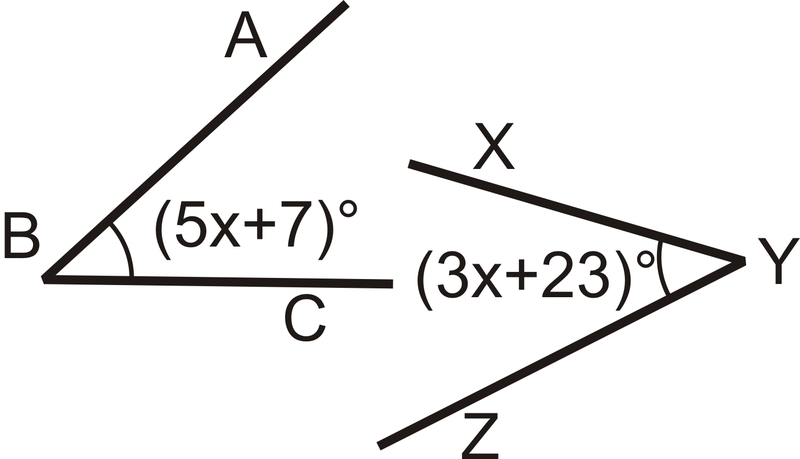    F-д_19А3А91ЕД 97А50933Б1Е1838Б97186Д7ФБ 3А75105Д7ФФА61Б867Д+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{5}\)

    Рішення

    З малюнка бачимо, що кути рівні.

    Встановіть рівні один одному кути і вирішуйте.

    \((5x+7)^{\circ} = (3x+23)^{\circ}\)

    \((2x)^{\circ}= 16^{\circ}\)

    \(x=8\)

    Щоб знайти міру\(\angle ABC\), підключіть\(x=8\) до

    \((5x+7)^{\circ} \rightarrow (5(8)+7)^{\circ} =(40+7)^{\circ}=47^{\circ}\).

    \(m \angle ABC=m \angle XYZ\)Тому що\(m \angle XYZ=47^{\circ}\) теж.

    Приклад\(\PageIndex{5}\)

    Чи\(\overline{OP}\) є кутова бісектриса\(\angle SOT\)?

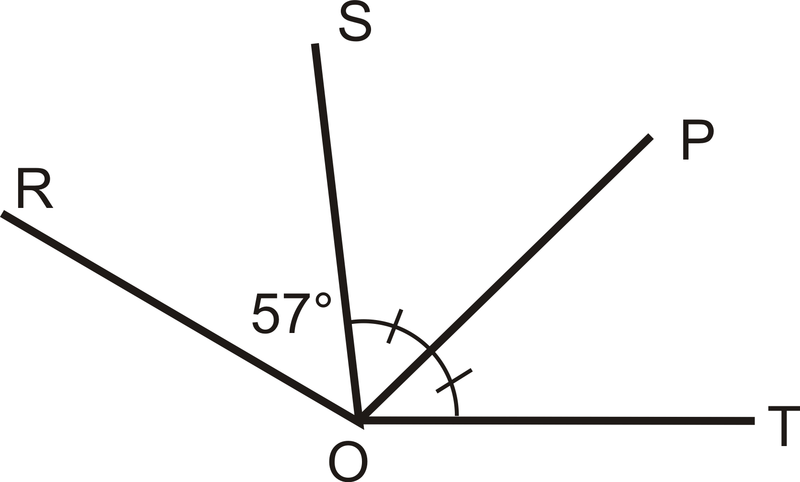    F-D_92F7C Баб 4609c583759544d246560a528091d5d5d5d37d6cc0a7b59efd+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{6}\)

    Рішення

    Так,\(\overline{OP}\) це бісектриса кута\(\angle SOT\) від розмітки на малюнку.

    Рецензія

    Для 1-4 використовуйте наступну картинку, щоб відповісти на запитання.

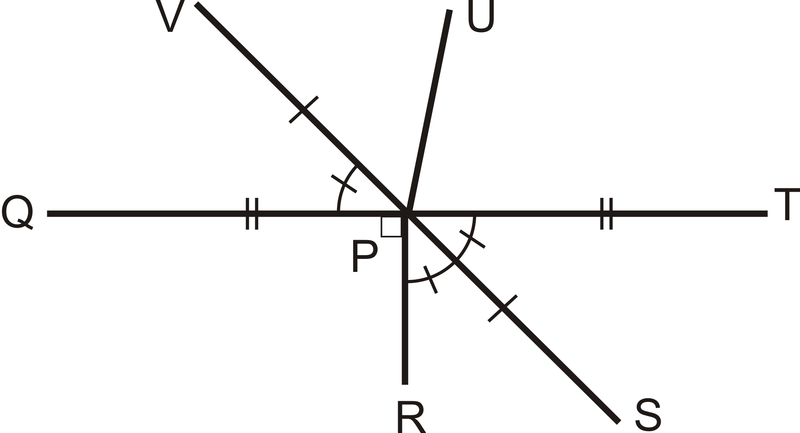    Ф-д_0е813Б80008999Б9Б9 бааа27Е076д 8989675Б02577С40Д06Ф 1Б1Б1С+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{7}\)
    1. Що таке бісектриса кута\(\angle TPR\)?
    2. Що таке\(m \angle QPR\)?
    3. Що таке\(m \angle TPS\)?
    4. Що таке\(m \angle QPV\)?

    Для 5-6 використовуйте алгебру для визначення значення змінної в кожній задачі.

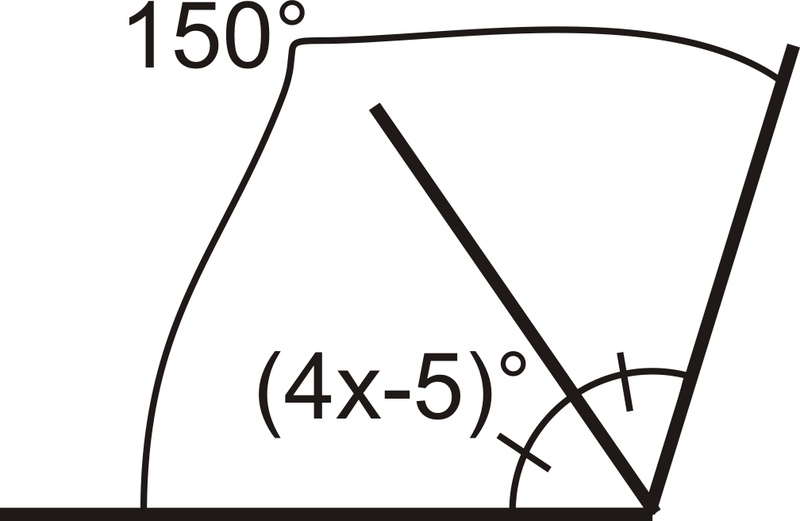    1. F-D_CA8Ф9A3187D23 Ед 68 Фе 3С0А6454 бусик 26БД 4860526Ф883А5318Ф6С1+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{8}\)
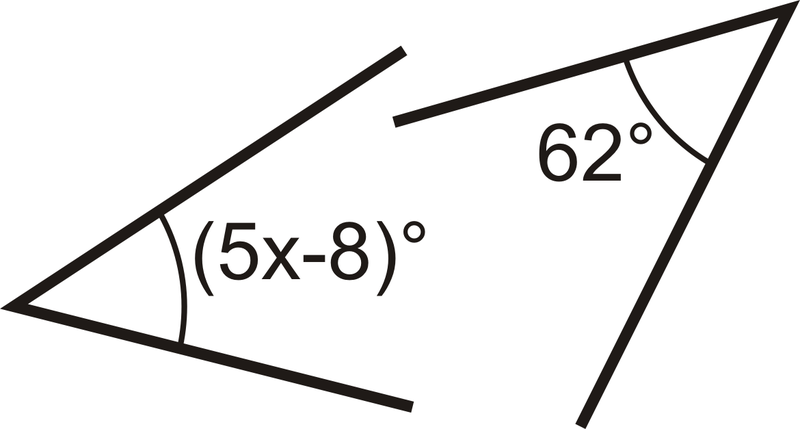    2. Ф-д_2С0343Ф435А9314009Б51С270ББ 049Д324САА0 ББ1Б917AEF1F859+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{9}\)

    За 7-10 вирішіть, чи є твердження істинним або хибним.

    1. Кожен кут має рівно одну бісектрису кута.
    2. Будь-яка розмітка на куті означає, що кут є\(90^{\circ}\).
    3. Бісектриса кута ділить кут на три конгруентних кута.
    4. Конгруентні кути мають однакову міру.

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.3.

    Лексика

    Термін Визначення
    бісектриса кута Бісектриса кута - це промінь, який розділяє кут на два конгруентні менші кути.
    Конгруентний Конгруентні фігури ідентичні за розміром, формою і мірою.

    Додатковий ресурс

    Інтерактивний елемент

    Відео: Принципи конгруентних кутів та бісектрис кута - Основні

    Діяльність: Конгруентні кути та кутові бісектриси Питання обговорення

    Навчальні посібники: Керівництво з вивчення кутів

    Практика: Конгруентні кути та бісектриси кута

    Реальний світ: Зоряна ніч