Skip to main content
LibreTexts - Ukrayinska

1.6: Точки, що розділяють сегменти лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    54954

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Формула перерізу знаходить координати точки, яка розбиває відрізок лінії в заданому співвідношенні.

    Нагадаємо, що медіана трикутника - це відрізок лінії, який з'єднує вершину трикутника з середньою точкою сторони, протилежної вершині. Всі трикутники мають три медіани, і ці три медіани перетинаються в одній точці, яка називається центроїдом, показана нижче. Центроїд розділяє кожну медіану в співвідношенні 2:1.

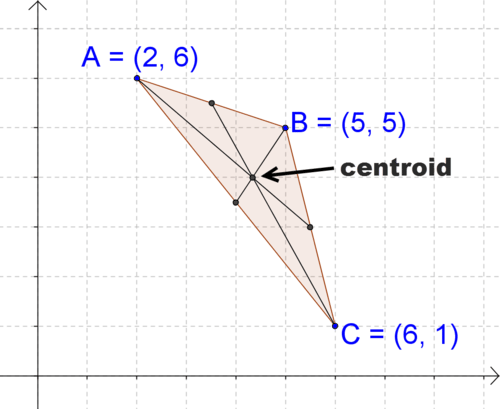    F-D_4B7E5867ec14494A67Bad02E1d7dc639d6E6E6E6E8A412E72DF3+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{1}\)

    Знайдіть координати центроїда, задані координати вершин трикутника, як показано на малюнку.

    Перегородки

    Припустимо, у вас є відрізок лінії\(\overline{AB}\). Точка\(P\) ділить цей відрізок лінії на дві частини такі, що\(AP=mk\) і\(PB=nk\). Можна сказати, що точкові\(P\) розділи\(AB\) сегментують у\(m:n\) співвідношенні. (Зверніть увагу\(\dfrac{mk}{nk}=mn\), що, співвідношення\(m:n\).)

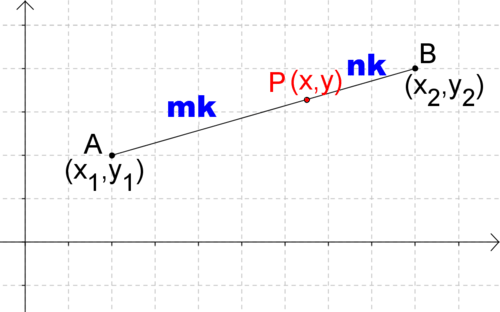    F-D_EB0877BF0B5AC2072d1d2E360B195950b6C78543F9287C14685F6+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{2}\)

    Природне питання, яке потрібно задати, - які координати точки\(P\)? Виходить, що за допомогою подібних трикутників і алгебри можна придумати формулу, яка дасть вам координати точки на\(P\) основі координат\(A\), координат і співвідношення\(m:n\).\(B\) Цю формулу іноді називають формулою розділу.

    Формула розділу: Задано\(\overline{AB}\) з\(A=(x_1, y_1)\) і\(B=(x_2, y_2)\), якщо\(P\) точкові розділи\(\overline{AB}\) у\(m:n\) співвідношенні, то координати точки P такі:

    \(P=\left (\dfrac{mx_{2}+nx_{1}}{m+n}, \dfrac{my_{2}+ny_{1}}{m+n}\right )\)

    Доведення подібності трикутника

    Для сегмента\(\overline{AB}\) нижче намалюйте два правильних трикутника, один з гіпотенузою\(\overline{AP}\) і один з гіпотенузою\(\overline{PB}\). Покажіть, що ці трикутники схожі.

    F-D_EB0877BF0B5AC2072d1d2E360B195950b6C78543F9287C14685F6+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{3}\)

    Почніть з малювання правильних трикутників. Нижче основа та висота кожного трикутника були позначені зеленим кольором.

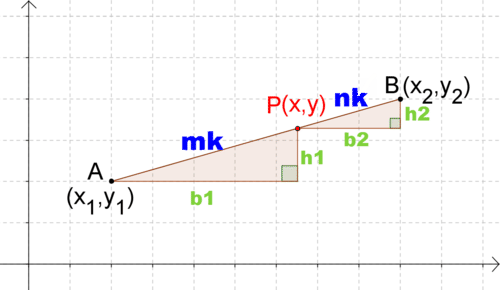    F-D_4DE3A05фак 419 CCCFB0D84EF08ad5957 CCEed01d7b6DFF9B287574+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{4}\)

    Зрозуміло, що ці трикутники мають одну пару конгруентних кутів (прямі кути). Яку ще інформацію ви маєте про трикутники? Ви знаєте, що для кожного трикутника співвідношення\(\dfrac{height}{base}\) - це нахил\(\overline{AB}\). Оскільки ці два трикутника прикріплені до одного відрізку лінії з однаковим нахилом, це означає, що\(\dfrac{h_1}{b_1} = {h_2}{b_2}\). Це еквівалентно\(\dfrac{b_2}{b_1}=\dfrac{h_2}{h_1}\). Дві пари сторін знаходяться в однаковому співвідношенні.

    Мало того, що існує одна пара конгруентних кутів, але є також дві пари відповідних сторін з однаковим співвідношенням. Трикутники схожі\(SAS\) на.

    Пошук довжини і висоти

    Знайдіть довжини основ і висоти кожного трикутника. Використовуйте той факт, що трикутники аналогічні для встановлення та вирішення пропорцій для,\(x\) а потім для\(y\) того, щоб знайти координати точки\(P\).

    F-D_4DE3A05фак 419 CCCFB0D84EF08ad5957 CCEed01d7b6DFF9B287574+зображення_thumb_поштова листівка_крихітка_зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{5}\)

    Основи і висоти можна знайти з точки зору\(x_1\),\(y_1\),\(x\),\(y\),\(x_2\),\(y_2\).

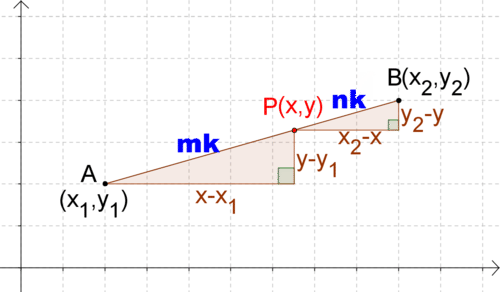    F-D_8B69AD5601519A9 AB8F2133E8A06868DBB00d6B2A40AC BBCe8A29B+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{6}\)

    Оскільки трикутники схожі, співвідношення між парами відповідних сторін рівні. Зокрема, ви знаєте:

    1. \(\dfrac{mk}{nk}=\dfrac{x−x_1}{x_2−x}\)
    2. \(\dfrac{mk}{nk}=\dfrac{y−y_1}{y_2−y}\)

    Ви можете використовувати алгебру для розв'язання першого рівняння для\(x\) та другого рівняння для\(y\).

    1. \(\dfrac{mk}{nk}=\dfrac{x−x_1}{x_2−x}\)\(\rightarrow \dfrac{m}{n}=\dfrac{x−x_1}{x_2−x} \)

    \(\rightarrow mx_2−mx=nx−nx_1\)

    \(\rightarrow mx_2+mx_1=mx+nx \)

    \(\rightarrow mx_2−nx_1=x(m+n)\)

    \(\rightarrow \dfrac{mx_2−nx_1}{m+n}=\dfrac{x(m+n)}{m+n}\)

    \(\rightarrow x=\dfrac{mx_2+nx_1}{m+n}\)

    1. \(\dfrac{mk}{nk}=\dfrac{y−y_1}{y_2−y}\)\(\rightarrow\dfrac{m}{n}=\dfrac{y−y_1}{y_2−y} \)

    \(\rightarrow my_2−my=ny−ny_1\)

    \(\rightarrow my_2+my_1=my+ny\)

    \(\rightarrow my_2−ny_1=y(m+n)\)

    \(\rightarrow \dfrac{my_2−ny_1}{m+n}=\dfrac{y(m+n)}{m+n}\)

    \(\rightarrow x=\dfrac{my_2+ny_1}{m+n}\)

    Точка\(P\) знаходиться на:

    \(P=\left(\dfrac{mx_2+nx_1}{m+n} ,\dfrac{my_2+ny_1}{m+n}\right)\)

    Пошук координат точки

    Розглянемо\(\overline{AB}\) з\(A=(10, 2)\) і\(B=(4, 1)\). \(P\)перегородки\(\overline{AB}\) в співвідношенні\(2:3\). Знайти координати точки\(P\).

    Ви можете використовувати формулу розділу з\((x_1,y_1)=(10, 2)\),\((x_2, y_2)=(4, 1)\),\(m=2\),\(n=3\).

    \(P=\left(\dfrac{mx_2+nx_1}{m+n} ,\dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{2 \cdot 4+3 \cdot10}{2+3}, \dfrac{2 \cdot 1+3\cdot 2}{2+3}\right)=\left(7.6,1.6\right)\)

    Ви можете намітити точки\(A\)\(B\), і\(P\) подивитися, чи реалістична ця відповідь.

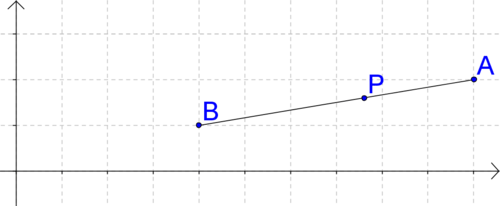    F-D_89210229F534C29A62B7C7CC 73DeF946C2F3C6343374AF5E64ED6+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_png\(\Індекс сторінки малюнка {7}\)

    Це виглядає так:\(P\) partitions the segment from \(A\) to \(B\) in a ratio of \(2:3\). Note that the answer would be different if you were looking for the point that partitioned the segment from \(B\) to \(A\). The order of the letters and “direction” of the segment matters.

    Example \(\PageIndex{1}\)

    Earlier, you were asked to find the coordinates of the centroid, given the coordinates of the vertices of the triangle as shown.

    f-d_4b7e5867ec140494a67bad02e1d7dc639d6e6eb8a69910a412e72df3+IMAGE_THUMB_POSTCARD_TINY+IMAGE_THUMB_POSTCARD_TINY.pngFigure \(\PageIndex{8}\)

    Solution

    One way to find the coordinates of the centroid is to use the section formula. You can focus on any of the three medians. Here, look at the median from point A. First, you will need to find the coordinates of the midpoint of \(\overline{BC}\) (the midpoint formula, a special case of the section formula, is derived in Guided Practice #1 and #2):

    \(\left(\dfrac{x_2+x_1}{2}, \dfrac{y_2+y_1}{2}\right)=\left (\dfrac{5+6}{2}, \dfrac{5+1}{2}\right)=\left(5.5,3\right )\)

    \(\left(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{2 \cdot 5.5+1 \cdot 2}{2+1}, \dfrac{2 \cdot 3+1 \cdot 6}{2+1}\right)=\left(\dfrac{13}{3}, 4\right)\)

    Looking at the picture, these coordinates for the centroid are realistic.

    Example \(\PageIndex{2}\)

    The midpoint of a line segment is the point exactly in the middle of the line segment. In what ratio does a midpoint partition a segment?

    Solution

    1:1, because the segments connecting the midpoint to each endpoint will be the same length.

    Example \(\PageIndex{3}\)

    The midpoint formula is a special case of the section formula where m=n=1. Derive a formula that calculates the midpoint of the segment connecting \((x_1,y_1)\) with \((x_2, y_2)\).

    Solution

    For a midpoint, \(m=n=1\). The section formula becomes:

    \(\left(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{x_2+x_1}{2}, \dfrac{y_2+y_1}{2}\right)

    This is the midpoint formula.

    Example \(\PageIndex{4}\)

    Consider \(\overline{BA}\) with \(B=(4, 1)\) and \(A=(10, 2)\). \(P\) partitions the segment in a ratio of \(2:3\). Find the coordinates of point \(P\). How and why is this answer different from the answer to Example \(C\)?

    Solution

    \((x_1, y_1)=(4,1)\) and \((x_2, y_2)=(10,2)\). \(m=2\) and \(n=3\).

    \(P=\left(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{2 \cdot 10+3 \cdot 4}{2+3}, \dfrac{2 \cdot 2+3 \cdot 1}{2+3}\right)=\left(6.4,1.4\right)\)

    This answer is different from the answer to Example C because in this case point P is partitioning the segment in a \(2:3\) ratio starting from point \(B\). In Example \(C\), you were starting from point \(A\).

    Review

    Find the midpoint of each of the following segments defined by the given endpoints.

    1. \((2, 6)\) and \((−4, 8)\)

    2. \((1, 9)\) and \((−2, 5)\)

    3. \((11, 24)\) and \((8, 12)\)

    4. \((1, 3)\) is the midpoint of \(\overline{AB}\) with \(A=(−2, 1)\). Find the coordinates of \(B\).

    5. \((2, 4)\) is the midpoint of \(\overline{CD}\) with \(C=(−5, 9)\). Find the coordinates of \(D\).

    6. \((4, 23)\) is the midpoint of \(\overline{EF}\) with \(E=(7, 11)\). Find the coordinates of \(F\).

    Consider \(A=(−9, 4)\) and \(B=(11, 17)\).

    7. Point \(P_1\) partitions the segment from \(A\) to \(B\) in a \(3:5\) ratio. Find the coordinates of point \(P_1\).

    8. Point \(P_2\) partitions the segment from \(B\) to \(A\) in a \(3:5\) ratio. Find the coordinates of point \(P_2\).

    9. Why are the answers to 7 and 8 different?

    10. Find the length of \(AP_1\) and \(P_2B\). Why should these lengths be the same?

    Consider \(C=(−6, −1)\) and \(D=(4, 8)\).

    11. Point \(P_3\) partitions the segment from \(A\) to \(B\) in a \(1:2\) ratio. Find the coordinates of point \(P_3\).

    12. Point \(P_4\) partitions the segment from \(B\) to \(A\) in a \(4:5\) ratio. Find the coordinates of point \(P_4\).

    13. Point \(P=(1, 2)\) partitions the segment from \(E=(9, 6)\) to \(F\) in a \(2:5\) ratio. Find the coordinates of point F.

    14. Point \(P=(−6, −4)\) partitions the segment from \(G=(−4, 6)\) to \(H\) in a \(5:3\) ratio. Find the coordinates of point \(H\).

    15. Point \(P=(6,8)\) partitions the segment from \(I=(−2,1)\) to \(J\) in a \(6:7\) ratio. Find the coordinates of point \(J\).

    16. A triangle is defined by the points \((5, 6)\), \((9, 17)\), and \((−2, 1)\). Find the coordinates of the centroid of the triangle.

    Review (Answers)

    To see the Review answers, open this PDF file and look for section 10.6.

    Vocabulary

    Term Definition
    centroid The centroid is the point of intersection of the medians in a triangle.
    Median The median of a triangle is the line segment that connects a vertex to the opposite side's midpoint.
    midpoint The midpoint of a line segment is the point on the line segment that splits the segment into two congruent parts.
    Midpoint Formula The midpoint formula says that for endpoints \((x_{1},y_{1})\) and \((x_{2},y_{2})\), the midpoint is \(\left (\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\).
    Partitions To partition is to divide into parts.
    Section Formula The section formula states how to find the coordinates of a point that partitions a line segment in a given ratio.

    Additional Resource

    Interactive Element

    Practice: Points that Partition Line Segments