1.7: Вступ до кутів
- Page ID
- 54957
Порівняння і класифікація кутів, таких як правильні або вертикальні, і їх відношення до ліній і променів.
Лінійний відрізок і промінь
Відрізок лінії - це частина лінії з двома кінцевими точками. Промінь - це частина лінії з однією кінцевою точкою. Лінійні сегменти називаються їх кінцевими точками, а промені називаються їх кінцевою точкою та іншою точкою. У кожному випадку над точками пишеться символ відрізка або променя. Внизу відрізок лінії є\(\overline{AB}\) і промінь\(\overrightarrow{AB}\).

Кути
- Коли два промені зустрічаються в їх кінцевих точках, вони утворюють кут.
- Залежно від ситуації кут може називатися символом кута\(\angle\) і його вершиною, або трьома буквами.
Якщо використовуються три літери, то середня буква повинна бути вершиною. Кут нижче можна було б назвати\(\angle B\) або\(\angle ABC\) або\(\angle CBA\). Використовуйте три літери, щоб назвати кут, якщо використання однієї літери не дасть зрозуміти, про який кут ви говорите.

Розмір кута вимірюється в градусах. Тому «міра кута ABC» відноситься до розміру або міри кута в градусах, часто пишуться\(m \angle ABC\). Ви можете використовувати транспортир або програмне забезпечення геометрії для вимірювання кутів. Пам'ятайте, що повне коло має\(360 ^{\circ}\).

види кутів
- Кут, який точно\(0 ^{\circ}\) називається нульовим кутом.
- Кут, який менше,\(90 ^{\circ}\) називається гострим кутом.
- Кут, який рівно\(90 ^{\circ}\) (одна чверть кола) називається прямим кутом. Відзначається прямий кут з невеликим квадратом у його вершині.
- Кут, який більше 90але менше,\(180 ^{\circ}\) називається тупим кутом. Кут, який рівно\(180 ^{\circ}\) (одна половина кола) називається прямим кутом.

Визначення типу кутів
Назвіть кут нижче і класифікуйте його за мірою.

\(m \angle F\)або\(m \angle DFE\) або\(m \angle EFD\). Це _____ кут.
Інтерактивний елемент
Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах
Інтерактивний елемент
Додаткові та додаткові кути
Два кути взаємодоповнюють, якщо сума їх мір дорівнює\(90 ^{\circ}\).

Два кути є додатковими, якщо сума їх мір дорівнює\(180 ^{\circ}\).

Два кута, які разом утворюють прямий кут, завжди будуть додатковими.
Пошук невідомого кута
\(x\)і\(y\) доповнюють кути з мірою\(y= 20^{\circ}\). Що таке міра\(x\)?

Міра\(x\) - _____.
Суміжні та вертикальні кути
Коли дві лінії перетинаються, утворюється безліч кутів, як показано нижче.
На схемі вище,\(\angle AEC\) і\(\angle AED\) знаходяться сусідні кути, тому що вони знаходяться поруч один з одним і поділяють промінь. Вони також є додатковими, тому що разом утворюють прямий кут. \(\angle AEC\)і\(\angle DEB\) називаються вертикальними кутами. Вертикальні кути завжди будуть мати однакову міру.
Розглянемо цей приклад проблеми:
Нехай\(m \angle AEC=x^{\circ}\). Покажіть, що також\(m \angle DEB\) має дорівнювати\(x^{\circ}\).

Це показує, що вертикальні кути завжди матимуть однакову міру.
Визначення кутів
Поясніть, чому ви повинні використовувати три літери, щоб визначити будь-який з кутів на діаграмі нижче.

Усі кути на цій діаграмі мають вершину E. Тому E неоднозначний, оскільки він може стосуватися багатьох різних кутів. Використовуйте три літери з E як середню літеру, щоб зрозуміти, який кут ви маєте на увазі\(\angle AEC\),\(\angle AED\),\(\angle DEB\),\(\angle BEC\).
Приклад\(\PageIndex{1}\)
Кути утворюються перетинаються лініями або променями. Якщо ви візьмете будь-які дві лінії або промені, ви сформуєте хоча б один кут?
Рішення
Поки лінії або промені перетинаються, буде утворюватися хоча б один кут. Якщо лінії (або промені) паралельні, а значить, не перетинаються, то ніякі кути не утворюються.

Приклад\(\PageIndex{2}\)
Оцініть міру кута\(\angle DFE\). Використовуйте транспортир, щоб підтвердити свою відповідь.
Рішення
Пам'ятайте, що рівно половина прямого кута - це\(45^{\circ}\). Цей кут виглядає більше половини прямого кута. Можна здогадатися, що це приблизно\(55^{\circ}\). Використовуючи транспортир, можна помітити, що мова йде про\(60^{\circ}\).
Приклад\(\PageIndex{3}\)
Які дві лінії, які утворюють прямий кут називається?
Рішення
Перпендикулярні лінії.
Інтерактивний елемент
Рецензія
1. Яка різниця між відрізком лінії, лінією та променем?
2. Намалюйте приклад прямого кута.
3. Намалюйте приклад тупого кута.
4. Намалюйте приклад гострого кута.
5. Чому два кути, які роблять прямий кут завжди додатковими?
6. Якщо\(m\angle ABC= (2x+4)^{\circ}\)\(m\angle DEF= (3x−5)^{\circ}\),\(\angle ABC\) і\(\angle DEF\) є доповнюючими, які міри кутів?
7. Якщо\(m\angle ABC= (2x+4)^{\circ}\)\(m\angle DEF= (3x−5)^{\circ}\),\(\angle ABC\) і\(\angle DEF\) є додатковими, які міри кутів?
Скористайтеся наведеною нижче схемою для #8 - #12.
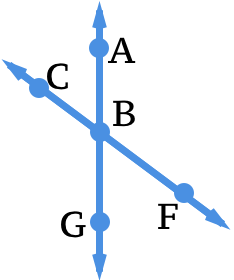 Малюнок\(\PageIndex{12}\)
Малюнок\(\PageIndex{12}\)8. Наведемо приклад вертикальних кутів.
9. Наведемо приклад прямого кута.
10. Наведемо приклад додаткових кутів.
11. Якщо\(m\angle ABC= 70^{\circ}\), знайдіть\(m\angle ABF\).
12. Якщо\(m\angle ABC= 70^{\circ}\), знайдіть\(m\angle FBG\).
13. Що ви пам'ятаєте про перпендикулярних лініях?
Використовуйте кут на зображенні для #14 - #15.
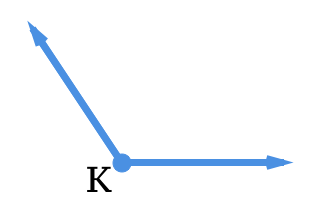 Малюнок\(\PageIndex{13}\)
Малюнок\(\PageIndex{13}\)14. Назвіть кут і класифікуйте його виходячи з його розміру.
15. Оцініть міру кута. Використовуйте транспортир, щоб підтвердити свою відповідь.
16. Намалюйте схему, на якій два кута є додатковими до одного і того ж кута. Що повинно бути правдою щодо оригінальних двох кутів? Поясніть.
17. Ми використовуємо термін комплементарний для опису кутів, які сумуються ___, і додаткові для опису кутів, які сумують ___. А як щодо кутів, які підсумовуються\(360^{\circ}\)? Придумайте назву для таких кутів і обгрунтуйте свій вибір.
18. Намалюйте два вертикальних кута. Наскільки повинен бути повернений кожен промінь одного з вертикальних кутів, щоб збігатися з іншим вертикальним кутом? Поясніть.
19. Намалюйте два кути однакової міри, які не є вертикальними. Намалюйте два кути, які є додатковими, але не суміжними. Намалюйте два кути, які є сусідніми і мають однакову міру. Яка міра кожного кута на останньому кресленні? Чому?
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, натисніть тут.