1.4: Середні точки та бісектриса сегмента

Last updated
Save as PDF

Page ID: 54965

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Використовуйте середні та бісектриси, щоб знайти позначку на півдорозі між двома координатами.

Коли два сегменти конгруентні, ми вказуємо, що вони конгруентні або однакової довжини з маркуванням сегментів, як показано нижче:

F-д_6А98А3Д 7Д0Ф7Е30Ф7 А6626д413А3Е250 ДДФ Ф 53Д0Б2Д22А146Ф08+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Середина - це точка на відрізку лінії, яка ділить його на два конгруентні відрізки.

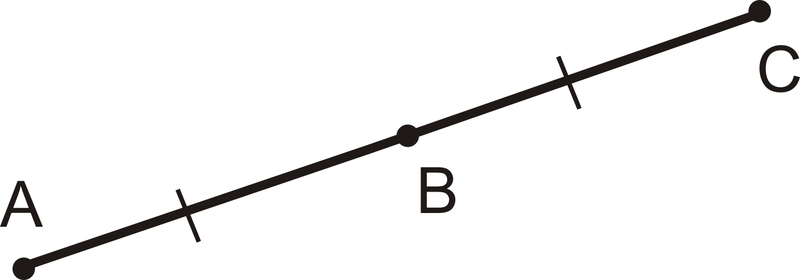Ф-Д_31д2Д6Б90116Б83С83КБСБ 107СБ 09938Ф38Ф38Д09105АС 9ДФ6427Е7+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Тому що\(AB=BC\),\(B\) є серединою\(\overline{AC}\). Будь-який відрізок лінії матиме рівно одну середину.

Коли точки побудовані в координатній площині, ми можемо використовувати формулу, щоб знайти середню точку між ними.

Ось два пункти,\((-5, 6)\) і\((3, 2).\)

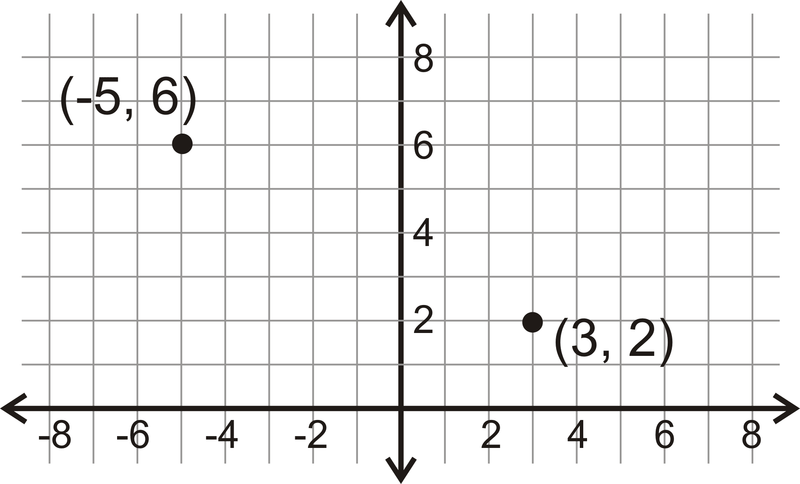F-D_650EA721AE597CC15733B51060539384713704655785 ДБ3409 CA65DE+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{3}\)

Середина повинна знаходитися на півдорозі між точками на відрізку, що з'єднує їх. Просто дивлячись, здається, що середина\((-1, 4).\)

Формула середньої точки: Для двох точок, (\(x_1, y_1\)) і (\(x_2,y_2\)), середина є\(\left (\dfrac{x_1+x_2}{2} , \dfrac{y_1+y_2}{2}\right) \).

Давайте використаємо формулу, щоб переконатися\((-1, 4)\), що це середина між\((-5, 6)\) і\((3, 2)\).

\(\left (\dfrac{-5+3}{2} ,\dfrac{6+2}{2}\right) =(−22,82)=(−1,4) \)

Бісектриса відрізка розрізає відрізок лінії на дві конгруентні частини і проходить через середню точку. Перпендикулярна бісектриса - це бісектриса відрізка, яка перетинає відрізок під прямим кутом.

\(\overline{AB} \cong \overline{BC}\)

\(\overline{AC} \perp \overleftrightarrow{DE}\)

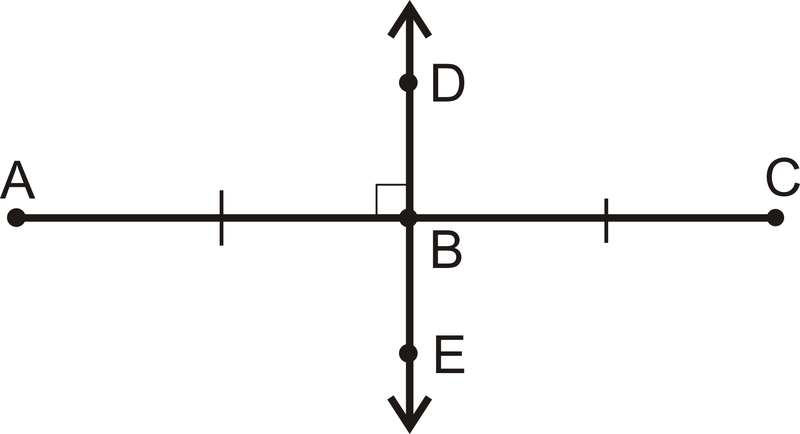F-д_10Б5С81Е8971228E3765Ф5БФ 8C316678e8E86850a8F859736F82BDCAAD1A+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{4}\)

Що робити, якщо вам дали координати двох точок і ви хотіли знайти точку точно посередині їх? Як би ви знайшли координати цієї третьої точки?

Приклад\(\PageIndex{1}\)

Напишіть всі однакові сегментні заяви.

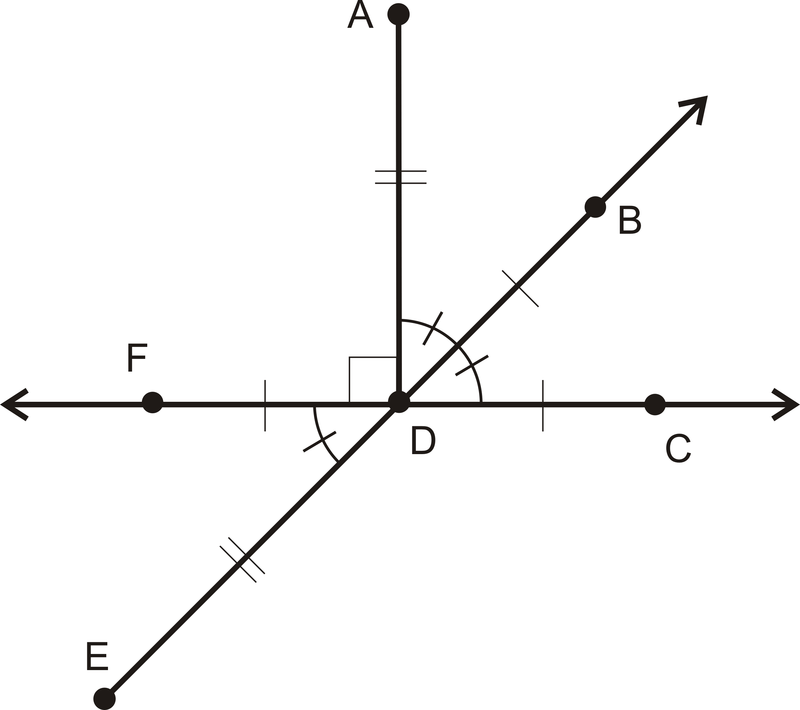F-д_9а 6700Е4Е1Д8Ф7С4722А6БФ 4668А0Б40КБ5ФБ6Б6БД46С24Б8Б8А1Е71Д+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

Рішення

\(AD=DE\)

\(FD=DB=DC\)

Приклад\(\PageIndex{2}\)

\(M\)Це середина\(\overline{AB}\)?

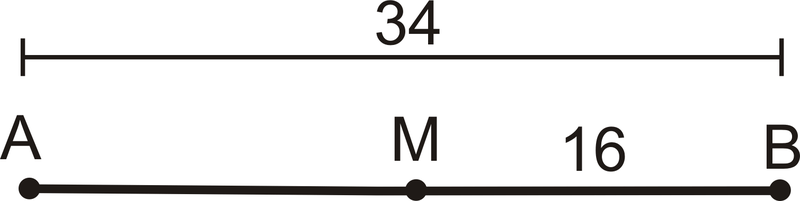
F-д_76АБ1ДДК9ААЕ00Б907Ф6Е17901А9А17ББ9ФБ9ФБ549АЕ9Е399097ФДБ6ФД+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

Рішення

Ні, це не так\(MB=16\) і\(AM=34−16=18\). \(AM\)повинен дорівнювати для\(MB\) того, щоб M була середньою точкою\(\overline{AB}\).

Приклад\(\PageIndex{3}\)

Знайдіть середню точку між\((9, -2)\) і\((-5, 14)\).

Рішення

Підключіть точки в формулу.

\(\left(\dfrac{9+(−5)}{2}\ ,\dfrac{−2+14}{2}\right)=\left(\dfrac{4}{2},\dfrac{12}{2}\right)=(2,6)\)

Приклад\(\PageIndex{4}\)

Якою лінією є перпендикулярна бісектриса\(\overline{MN}\)?

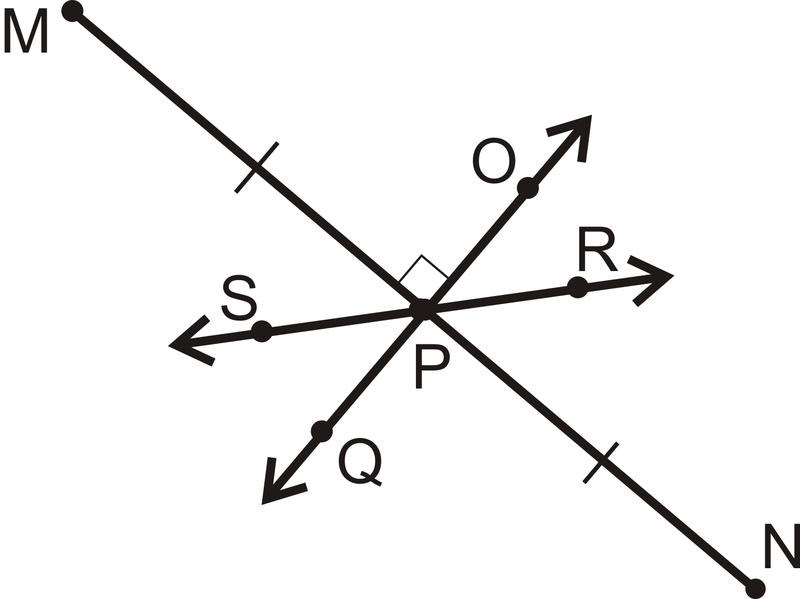F-д_ЕБ304884693938А 38Д56БФ 2БД Ф Ф Ф 528Ф4А3Е963С0091768ФБ3056D+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

Рішення

Перпендикулярна бісектриса повинна бути бісекційною\(\overline{MN}\) і бути перпендикулярною їй. Тільки\(\overleftrightarrow{OQ}\) підходить під цей опис. \(\overleftrightarrow{SR}\)є бісектриса, але не перпендикулярна.

Приклад\(\PageIndex{5}\)

Знайти\(x\) і\(y\).

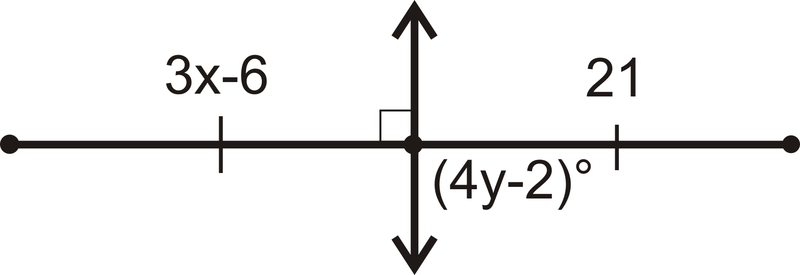Ф-Д_749 КФ80ДБА 8ФБ29Б27Б801Д636209Е36994Ф8Е53ФБ 86Б145C35FF53+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Рішення

Показана лінія - перпендикулярна бісектриса.

Отже,\(3x−6=21\)

\(3x=27\)

\(x=9\)

І,\((4y−2)=90\)

\(4y=92\)

\(y=23\)

Рецензія

Скопіюйте малюнок нижче і позначте його наступною інформацією:

\(\overline{AB} \cong \overline{AD}\)

\(\overline{CD} \cong \overline{BC}\)

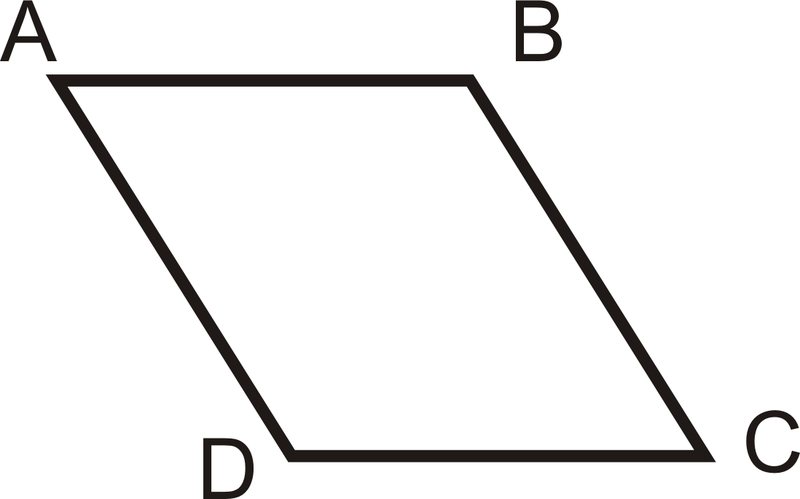F-D_9A867539E404ББА 62ДА 8 АФ 4Е566Ф7Б4Ф90А209239Ф13Б447100 ЕЕДА+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{9}\)

Для 2-4 використовуйте наступну картинку, щоб відповісти на питання.

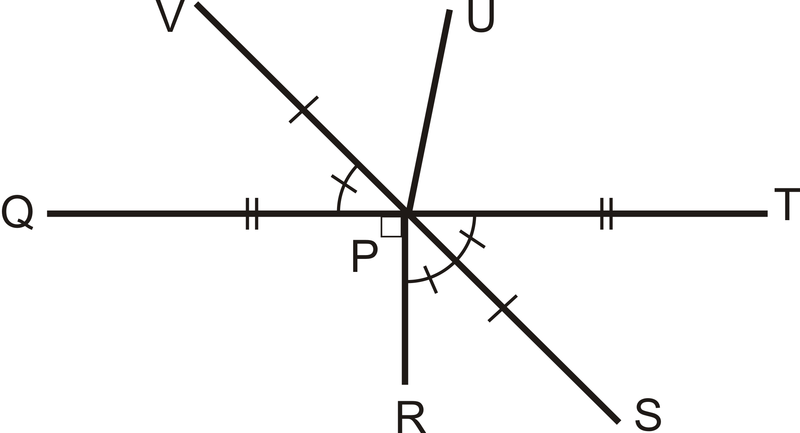Ф-д_0е813Б80008999Б9Б9 бааа27Е076д 8989675Б02577С40Д06Ф 1Б1Б1С+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

\(P\)середина того, що два сегменти?
Як\(\overline{VS}\) ставиться до\(\overline{QT}\)?
Як\(\overline{QT}\) ставиться до\(\overline{VS}\)?

Для вправи 5 використовуйте алгебру для визначення значення\(x\).

Малюнок\(\PageIndex{11}\)

Для питань 6-10 знайдіть середину між кожною парою точок.

(-2, -3) і (8, -7)
(9, -1) і (-6, -11)
(-4, 10) і (14, 0)
(0, -5) і (-9, 9)
(-3, -5) і (2, 1)

Враховуючи середню точку (\(M\)) та будь-яку кінцеву точку\(\overline{AB}\), знайдіть іншу кінцеву точку.

\(A(−1,2)\)і\(M(3,6)\)
\(B(−10,−7)\)і\(M(−2,1)\)

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 1.4.

Лексика

Термін	Визначення
середина	Середина відрізка лінії - це точка на відрізку лінії, яка розділяє відрізок на дві конгруентні частини.
перпендикулярна бісектриса	Бісектриса відрізка, яка перетинає відрізок під прямим кутом.
бісектриса сегмента	Бісектриса відрізка - це лінія (або частина лінії), яка проходить через середню точку.
маркування сегментів	Коли два сегменти конгруентні, ми вказуємо, що вони збігаються з *маркуванням сегментів*.
Формула середньої точки	Формула середньої точки говорить, що для кінцевих точок\((x_1, y_1)\) і\((x_2, y_2)\), середина є\( \left (\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\).

Додаткові ресурси

Інтерактивний елемент

Відео: Середні точки та бісектриси сегментів Приклади - Основні

Діяльність: Середні точки та сегментні бісектриси Питання обговорення

Навчальні посібники: Керівництво з вивчення сегментів

Практика: Середні точки та бісектриси сегментів

Реальний світ: середина та сегментні бісектриси - діяльність пошуку скарбів