Skip to main content
LibreTexts - Ukrayinska

1.3: Визначення відрізків лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    54979

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Визначте позитивну довжину між точками.

    Вимірювання відстані між двома точками

    Відстань - це міра довжини між двома точками. Виміряти - це визначити, наскільки далеко один від одного два геометричні об'єкти. Найпоширеніший спосіб вимірювання відстані - за допомогою лінійки. Дюймові лінійки зазвичай поділяються на восьмидюймові (або 0,125 дюйма) сегменти. Сантиметрові лінійки діляться вгору десятосантиметровими (або 0,1 см) відрізками. Зверніть увагу, що відстань між двома точками - це абсолютне значення різниці між числами, показаними на лінійці. Це означає, що вам не потрібно починати вимірювання з «0», якщо ви віднімаєте перше число з другого.

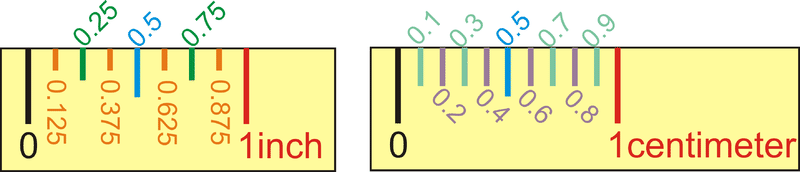    F-д_3ДФ 110041АЕЦБК080ЕБ9Д5514613Б2 ЕЕ8Д11Е086А9Б6Е01БД2ДЕ0+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{1}\)

    Постулат додавання сегмента стверджує, що якщо\(A\)\(B\), і\(C\) є колінеарними і\(B\) знаходиться між\(A\) і\(C\), то\(AB+BC=AC\).

    F-D_436C14CC166A 2505476266587ФФ ЕДД332512Е64С748Б31А4ДБ 6962+зображення_крихіткий+зображення_крихітка_крихіткий.PNGМалюнок\(\PageIndex{2}\)

    Ви можете знайти відстані між точками на\(x–y\) площині, якщо лінії горизонтальні або вертикальні. Якщо рядок вертикальний, знайдіть зміну\(y\) −coordinates. Якщо лінія горизонтальна, знайдіть зміну\(x\) −coordinates.

    Припустимо, ви хочете виміряти свій зріст, але рулетка у вас є стара і кінець відламаний. Якщо стрічка зараз починається з 6 см і читає 138 см від підлоги до верхівки голови, який ви високий?

    Приклад\(\PageIndex{1}\)

    Яке відстань позначено на лінійці нижче? Лінійка знаходиться в сантиметрах.

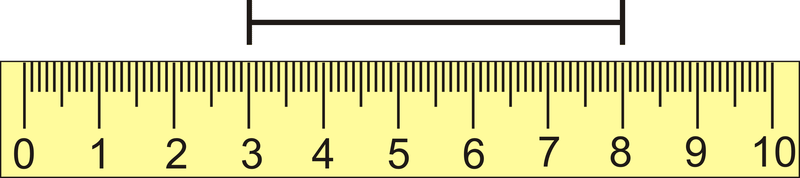    Ф-д_С2Б23827Е0519А2А87А9399Ф5Е59 БФ ФАДА 756Д2Ф97Б299C8E1E8E7F+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{3}\)

    Рішення

    Відніміть одну кінцеву точку від іншої. Відрізок лінії охоплює від 3 см до 8 см.

    \(|8−3|=|5|=5\)

    Відрізок лінії довжиною 5 см. Зверніть увагу, що ви також могли б зробити

    \(|3−8|=|−5|=5\).

    Приклад\(\PageIndex{2}\)

    Складіть ескіз того\(\overline{OP}\), де\(Q\) знаходиться між\(O\) і\(P\).

    Рішення

    Намалюйте\(\overline{OP}\) спочатку, потім розмістіть\(Q\) на відрізку.

    F-д_0БК 9ДА2 ЦЕЕ402168Ф41Д62663Д 344677216 СД065А02С2Б68959083C2+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{4}\)

    Приклад\(\PageIndex{3}\)

    Яка відстань між двома точками, показаними нижче?

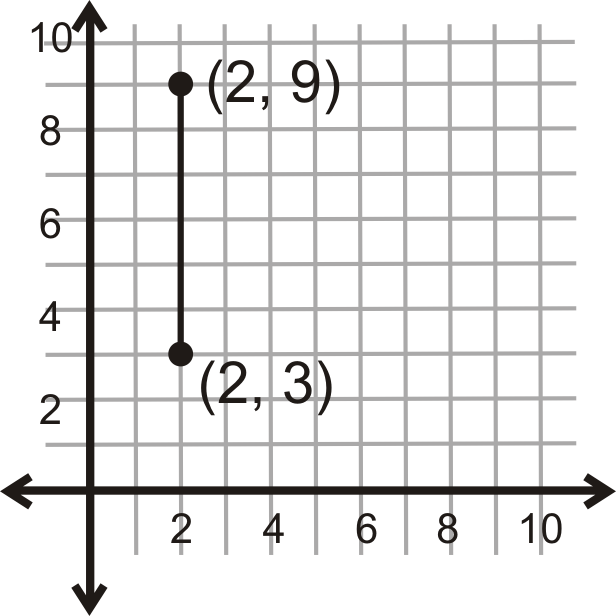    F-д_7659965 ЕФ 21 ЕЕА 21Ф846С8 Е27 А674148Б4593А63А6313 АА7AF05A35+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{5}\)

    Рішення

    Оскільки ця лінія вертикальна, подивіться на зміну\(y\) -координат.

    \(|9−3|=|6|=6\)

    Відстань між двома точками - 6 одиниць.

    Приклад\(\PageIndex{4}\)

    На зображенні з прикладу 2, якщо\(OP=17\) і\(QP=6\), що таке\(OQ\)?

    Рішення

    \(OQ+QP=OP\)

    \(OQ+6=17\)

    \(OQ=17−6\)

    \(OQ=11\)

    Приклад\(\PageIndex{5}\)

    Яка відстань між двома точками, показаними нижче?

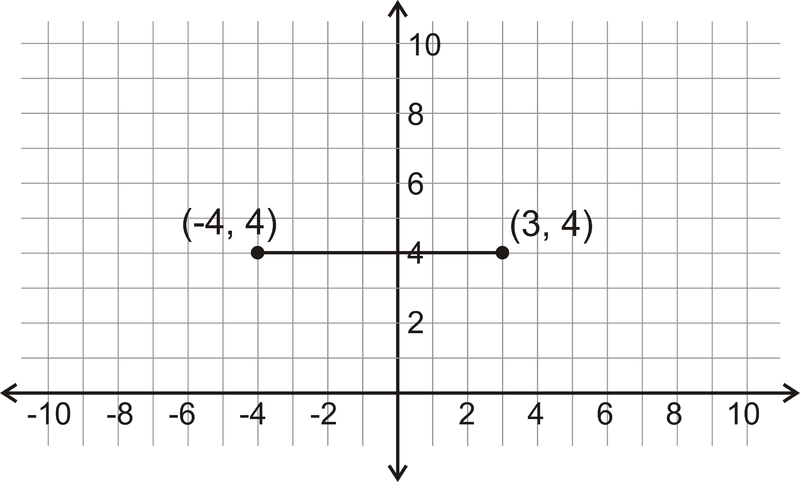    F-D_1756425B14D9E56A0049874E50FF4E1 Каб 6ЕФ1Ф28 Ацееб 95CB14C215+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{6}\)

    Рішення

    Оскільки ця лінія горизонтальна, подивіться на зміну\(x\) -координат.

    \(|(−4)−3|=|−7|=7\)

    Відстань між двома точками становить 7 одиниць.

    Рецензія

    Для 1-4 використовуйте лінійку на кожній картинці, щоб визначити довжину відрізка лінії.

    1. F-д_86Б68 АФ 9799Ф07Ф 5660D467C1ЕЕС81D1164 КАД066Д8Ф983343 ЦББ75+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{7}\)
    2. F-д_Ф6930Д2БФ71Ф030654 ААААФ 493293Б14460255ДДБ 1А19ДБ31С308АА+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{8}\)
    3. F-D_746Ф3Д7Б7Б8Ф61Ф14594 БФ ФЧ 89197д76503C2264F4AE0DB6547917E+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{9}\)
    4. Ф-Д_7СС25АК 89СС3Б2БД02А95045 CF67 А2593А59С0890ДФ 3БДА683Ф4+зображення_крихіткий+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{10}\)
    5. Зробити ескіз\(\overline{BT}\), з\(A\) між\(B\) і\(T\).
    6. Якщо O знаходиться в середині\(\overline{LT}\), де саме він розташований? Якщо\(LT=16 cm\), що таке\(LO\) і\(OT\)?
    7. Для трьох колінеарних точок,\(A\) між\(T\) і\(Q\):
      1. Намалюйте ескіз.
      2. Напишіть постулат додавання сегментів для вашого ескізу.
      3. Якщо\(AT=10\) в і\(AQ=5\) в, що таке\(TQ\)?
    8. Для трьох колінеарних точок,\(M\) між\(H\) і\(A\):
      1. Намалюйте ескіз.
      2. Напишіть постулат додавання сегментів для вашого ескізу.
      3. Якщо\(HM=18 cm\) і\(HA=29 cm\), що таке\(AM\)?
    9. Для трьох колінеарних точок I між M і T:
      1. Намалюйте ескіз.
      2. Напишіть постулат додавання сегментів для вашого ескізу.
      3. Якщо\(IT=6 cm\) і\(MT=25 cm\), що таке\(AM\)?
    10. Зробіть ескіз, який відповідає опису: B знаходиться між\(A\) і\(D\). \(C\)знаходиться між\(B\) і\(D\). \(AB=7 cm\),\(AC=15 cm\), і\(AD=32 cm\). Знайти\(BC\),\(BD\), і\(CD\).
    11. Складіть ескіз, який відповідає опису:\(E is between \(F\) і\(G\). \(H\)знаходиться між\(F\) і\(E\). \(FH=4 in\),\(EG=9 in\), і\(FH=HE\). Знайти\(FE\),\(HG\), і\(FG\).

    Для 12 і 13, Припустимо,\(J\) знаходиться між\(H\) і\(K\). Скористайтеся Постулатом додавання сегментів, щоб вирішити для\(x\). Потім знайдіть довжину кожного відрізка.

    1. \(HJ=4x+9\),\(JK=3x+3\),\(KH=33\)
    2. \(HJ=5x−3\),\(JK=8x−9\),\(KH=131\)

    Для 14-17 визначте вертикальну або горизонтальну відстань між двома точками.

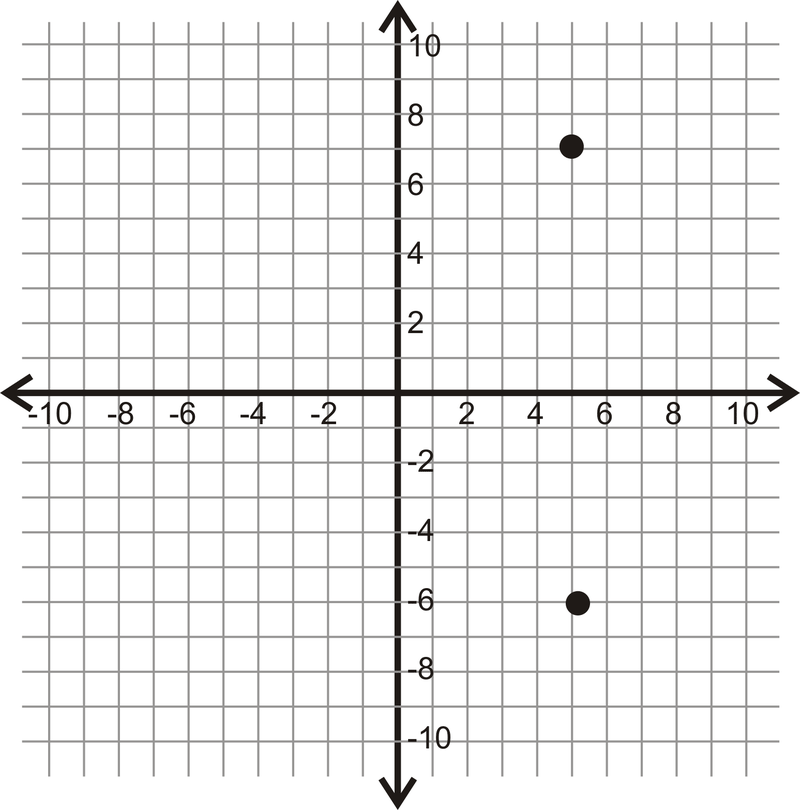    1. Ф-д_Е7Д5Б14А971143144 ДД4Ф13А05Е3Б6КД2Ф8Ф93Д27С8Б2Е15ЕБАФ0+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{11}\)
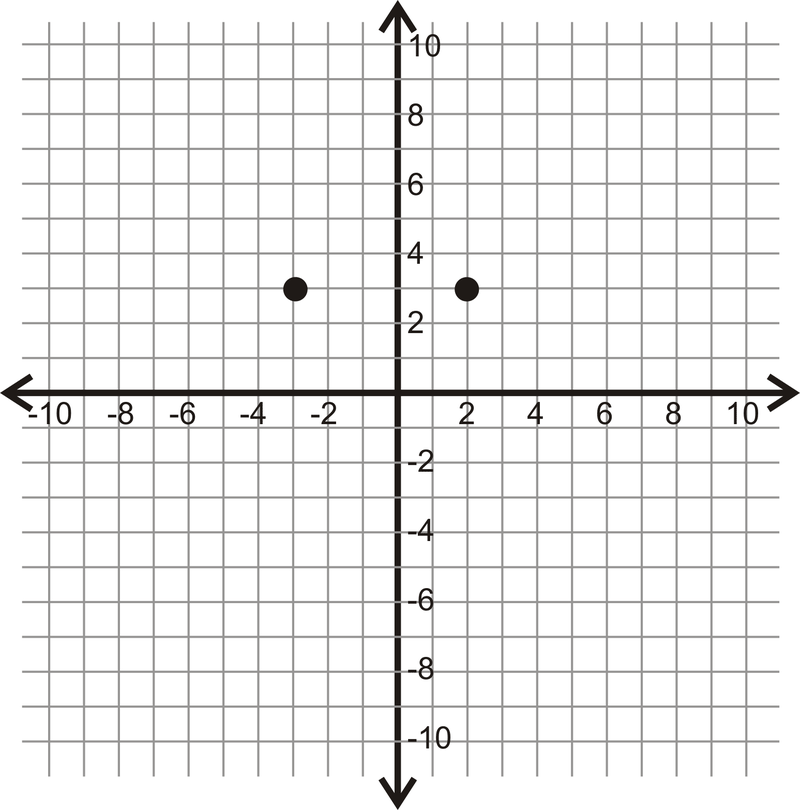    2. F-D_9086C867C93527B9508457 ЕФ Ф 790Е5Е5А611Ф95375252ДДДД027923+зображення_крихіткий+зображення_крихіткий_pngМалюнок\(\PageIndex{12}\)
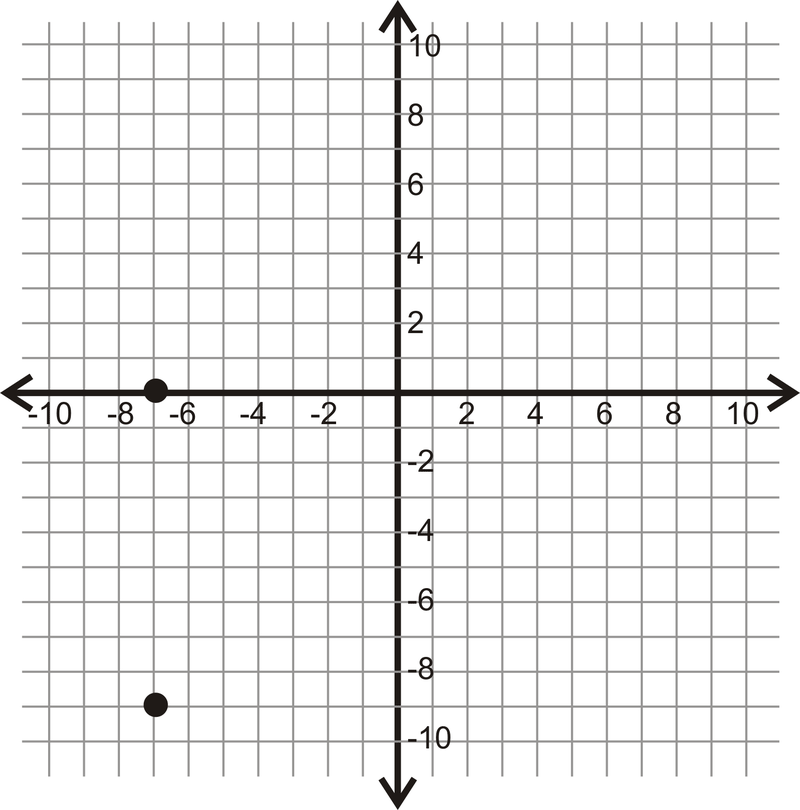    3. F-D_14642892E678 АББ 8850253474 ЕС9Б9А3ФА8Д5ФА88DA66719039D4E08+зображення_крихіткий+зображення_крихіткий_крихіткий.PNGМалюнок\(\PageIndex{13}\)
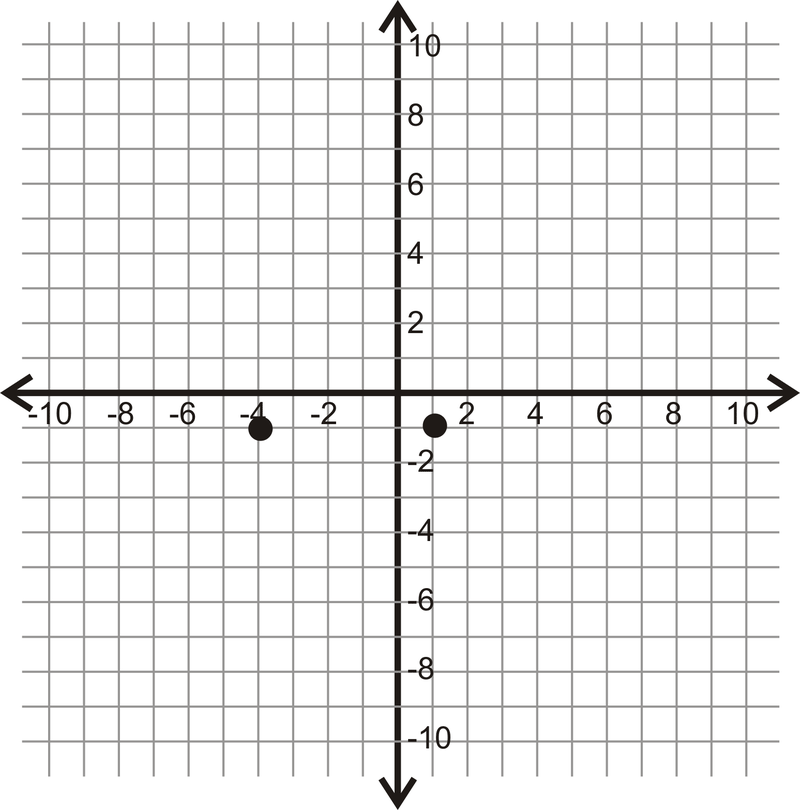    4. FF-д_АЕ5ФД 118515Е 757163Б1171Ф 3848 де 8117DA69946527288БК729DF0+зображення_крихіткий+зображення_крихіткий.PNG Малюнок\(\PageIndex{14}\)
    5. Складіть ескіз:\(S\) знаходиться між\(T\) і\(V\). \(R\)знаходиться між\(S\) і\(T\). \(TR=6\),\(RV=23\), і\(TR=SV\).
    6. Знайти\(SV\)\(TS\),\(RS\) і\(TV\) від #18.
    7. Бо\(\overline{HK}\), припустимо, що\(J\) знаходиться між\(H\) і\(K\). Якщо\(HJ=2x+4\)\(JK=3x+3\), і\(KH=22\), знайти\(x\).

    Лексика

    Термін Визначення
    відстань Відстань - це міра довжини між двома точками.
    Абсолютна величина Абсолютне значення числа - це відстань, на якій знаходиться число від нуля. Абсолютні значення ніколи не бувають негативними.
    міра Виміряти відстань - це визначити, наскільки далеко один від одного два геометричні об'єкти за допомогою цифрової лінії або лінійки.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Постулат лінійки і постулат додавання сегмента

    Діяльність: Відстань між двома пунктами Питання обговорення

    Навчальні посібники: Керівництво з вивчення сегментів

    Практика: Визначення відрізка лінії

    Реальний світ: Відстань між двома точками