Skip to main content
LibreTexts - Ukrayinska

6.3.5: Гіперболи та асимптоти

  1. Last updated
  2. Save as PDF
  • Page ID
    55080

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Гіперболи і асимптоти

    Як і інші конічні перерізи, гіперболи можна створити, «нарізаючи» конус і дивлячись на поперечний переріз. На відміну від інших коніків, гіперболи насправді вимагають 2 конуси, складені один на одного, вказують на точку. Форма - результат ефективного створення параболи з обох шишок одночасно.

    Отже, питання полягає в тому, чи дійсно гіперболи вважаються формою самостійно? Або вони лише дві параболи графовані одночасно? Чи можна зробити «різні» форми з будь-якого з інших конічних перерізів, якби використовувалися одночасно два конуса?

    Гіперболи і асимптоти

    Крім своєї вогнищевої властивості, гіперболи мають ще одне цікаве геометричне властивість. На відміну від параболи, гіпербола стає нескінченно близькою до певної лінії, коли координати x− або y−координати наближаються до нескінченності. Що ми маємо на увазі під «нескінченно близьким»? Тут ми маємо на увазі дві речі: 1) Чим далі ви йдете по кривій, тим ближче ви підходите до асимптоти, і 2) Якщо ви називаєте відстань, незалежно від того, наскільки маленькою, врешті-решт крива буде такою близькою до асимптоти. Або, використовуючи мову меж, як ми йдемо далі від вершини гіперболи межа відстані між гіперболою і асимптотою дорівнює 0.

    Ці лінії називаються асимптотами.

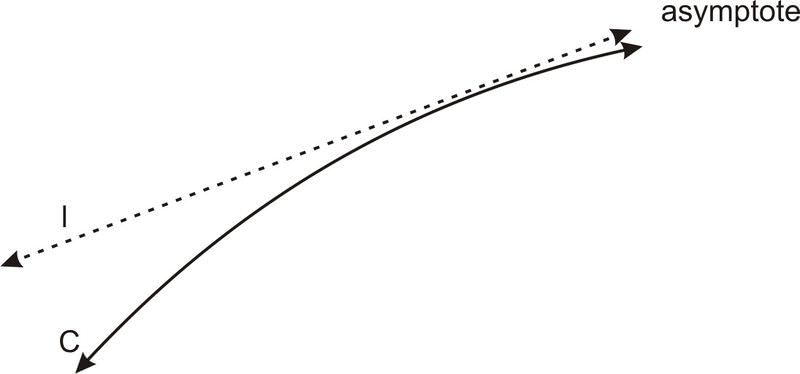
    Ф-Д_50Е3 ЕЕБФ 6Д270442Ф5Б62 ЕФДБ01935Ф БД9928Д88БФД 9АЕ4АЦ8Б+зображення_крихіткий+зображення_крихіткий.jpg

    Існує два асимптоти, і вони перетинаються в точці, в якій знаходиться гіпербола по центру:

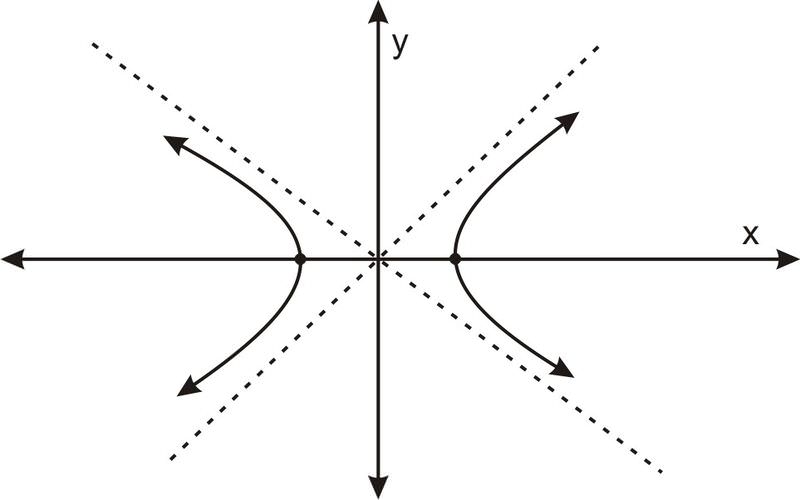
    Ф-Д_6С 60Ф9Б9 СА22206С9572053 ББД АЦ9Б4653ФА6Б9Д965Д19Д5Ф+зображення_крихіткий+зображення_крихіткий.jpg

    Для гіперболи форми\(\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) асимптотами служать лінії:

    \(\ y=\frac{b}{a} x\)і\(\ y=-\frac{b}{a} x\).

    Для гіперболи форми\(\ \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) асимптотами є лінії:

    \(\ y=\frac{a}{b} x\)і\(\ y=-\frac{a}{b} x\).

    (Для зміщеної гіперболи асимптоти зміщуються відповідно.)

    Приклади

    Приклад 1

    Раніше вас запитали, чи слід вважати гіперболами форми все своїми.

    Рішення

    Гіперболи вважаються різними формами, оскільки існують специфічні форми поведінки, унікальні для гіпербол. Крім того, хоча гіперболи є результатом подвійних парабол, жоден з інших коніків насправді не створює унікальних форм з подвійними конусами - лише подвійними фігурами - і в будь-якому випадку вимагають декількох «зрізів».

    Приклад 2

    Графік наступної гіперболи, малюючи її вогнища і асимптоти і використовуючи їх для створення кращого малюнка:\(\ 9 x^{2}-36 x-4 y^{2}-16 y-16=0\)

    Рішення

    Спочатку ставимо гіперболу в стандартну форму:

    \ (\\ почати {вирівняний}
    9\ ліворуч (x^ {2} -4 х\ праворуч) -4\ ліворуч (y^ {2} +4 y\ праворуч) &=16\
    9\ ліворуч (x^ {2} -4\ праворуч) -4\ ліворуч (y^ {2} +4\\ праворуч) &= 36\\\ frac {(x-2) ^ {2}} {4}
    \\ правий) &=36\\ frac {(x-2) ^ {2}} {4}\ гідророзрив {(y+2) ^ {2}} {9} &=1
    \ кінець {вирівняний}\)

    Отже\(\ a=2\),\(\ b=3\) і\(\ c=\sqrt{4+9}=\sqrt{13}\). Гіпербола орієнтована горизонтально, по центру в точці\(\ (2,-2)\), з осередками в\(\ (2+\sqrt{13},-2)\) і\(\ (2-\sqrt{13},-2)\). Після зсуву до уваги асимптотами є лінії:\(\ y+2=\frac{3}{2}(x-2)\) і\(\ y+2=-\frac{3}{2}(x-2)\). Отже, графікуючи вершини та кілька точок з обох боків, ми бачимо, що гіпербола виглядає приблизно так:

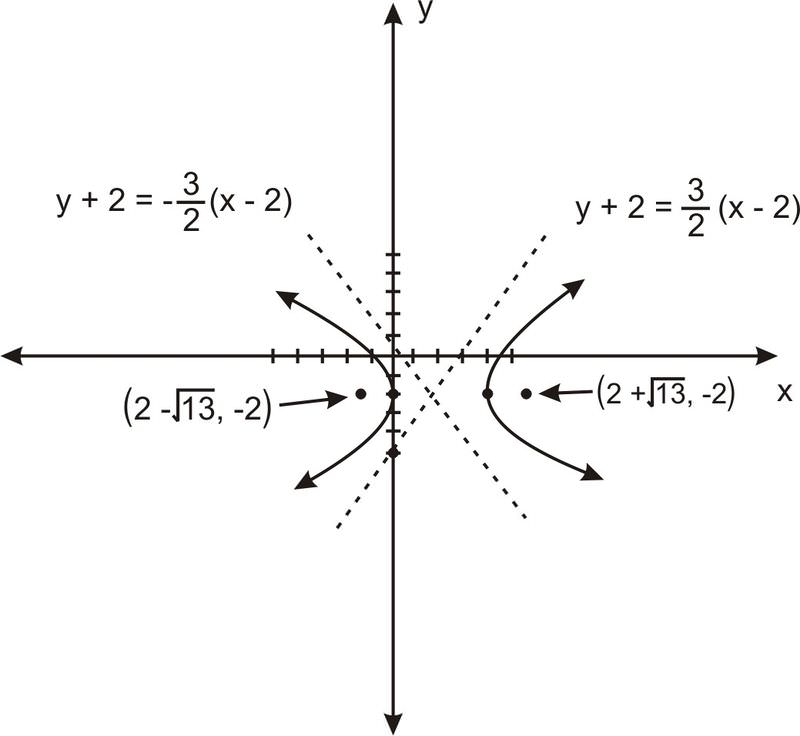
    Ф-Д_420Ф0Ф 619 АД 6БК АЕ 8Ф5Б89С2Б24Ф8Ф83Е7Ф7ФЦ51975А1С27 ББК 32+зображення_крихіткий+зображення_крихіткий.jpg

    Приклад 3

    Графік наступної гіперболи, малюючи її вогнища і асимптоти і використовуючи їх для створення кращого малюнка:\(\ 16 x^{2}-96 x-9 y^{2}-36 y-84=0\)

    Рішення

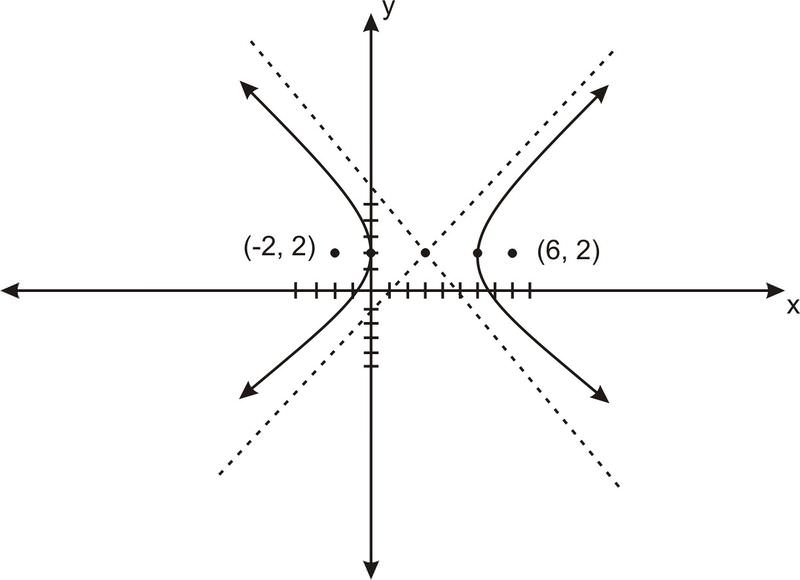
    Ф-Д_94Е24С8Д904308 ББФ 4Д34916Б555Ф5А6Д76СЕ11А87Ф102А1Б607Ф3Ф2+зображення_крихіткий+зображення_крихіткий.jpg

    Приклад 4

    Графік наступної гіперболи, малюючи її вогнища і асимптоти, і використовуйте їх для створення кращого малюнка:\(\ y^{2}-14 y-25 x^{2}-200 x-376=0\).

    Рішення

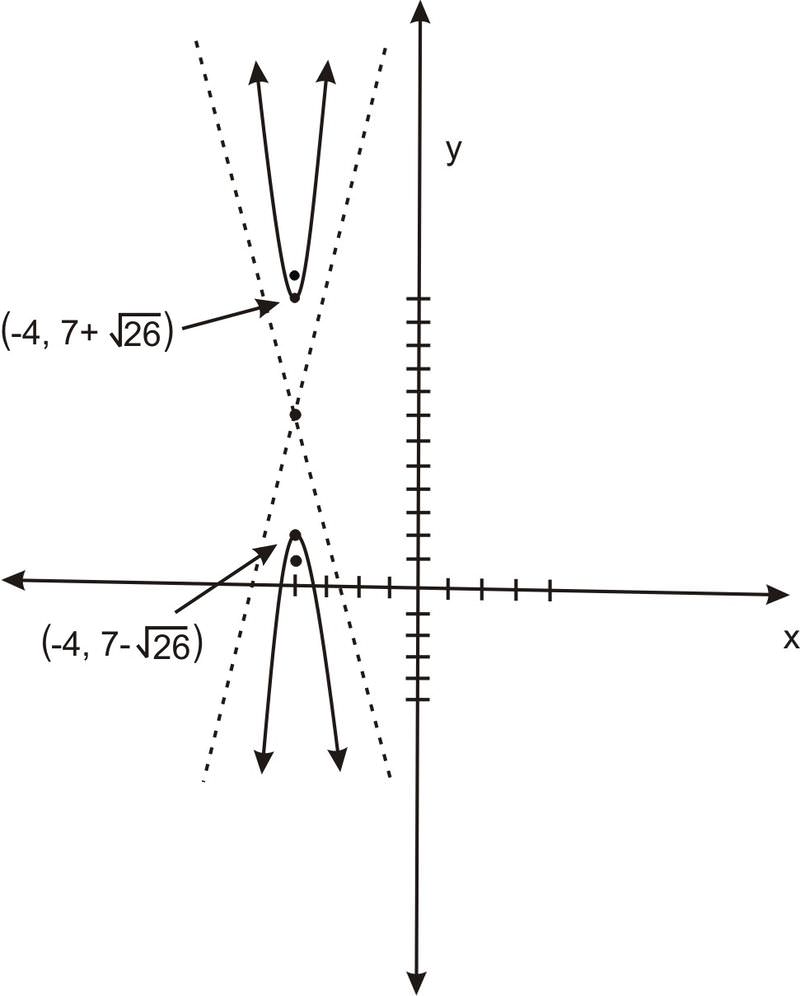
    Ф-Д_Е2 ДДД0С5СД8694Е4Е4БДФ 38ФБ BB12B7CDCF6F828E63449D031AE6C+зображення_крихіткий+зображення_крихіткий.jpg

    Приклад 5

    Знайдіть рівняння для гіперболи з асимптотами нахилів\(\ \frac{5}{12}\) і\(\ -\frac{5}{12}\), і вогнищами в точках\(\ (2,11)\) і\(\ (2,1)\).

    Рішення

    \(\ \frac{(y-6)^{2}}{25}-\frac{(x-2)^{2}}{144}=1\)

    Приклад 6

    Гіпербола з перпендикулярними асимптотами називається перпендикулярної. Як виглядає рівняння перпендикулярної гіперболи?

    Рішення

    Нахили перпендикулярних ліній - негативні зворотні один одному. Це означає те\(\ \frac{a}{b}=\frac{b}{a}\), що, для позитиву\(\ a\) і\(\ b\) означає\(\ a=b\).

    Приклад 7

    Знайдіть рівняння гіперболи з х-перехопленнями в\(\ x = –7\) і\(\ x = 5\), а вогнища при\(\ (–6, 0)\) і\(\ (4, 0)\).

    Рішення

    Вогнища мають однакові y-координати, тому це ліва/права гіпербола з центром, вогнищами та вершинами на лінії, що паралельна осі x.

    Оскільки це ліва/права гіпербола, y частина рівняння буде від'ємною, і рівняння буде вести з\(\ x^{2}\) терміном (оскільки провідний член є позитивним за умовністю, а квадратний член повинен мати різні ознаки, якщо це гіпербола).: Центр знаходиться посередині між вогнищами, тому центр \(\ (h, k)=(-1,0)\). Вогнища c складають 5 одиниць в обидві сторони від центру, так\(\ c=5 \rightarrow c^{2}=25\).

    X-перехоплення - це 4 одиниці в обидві сторони від центру, а фокуси знаходяться на осі x, тому перехоплення повинні бути вершинами\(\ a\)\(\ a=4 \rightarrow a^{2}=16\).

    Використовуйте теорему Піфагора,\(\ a^{2}+b^{2}=c^{2}\), щоб отримати\(\ b^{2}=25-16=9\).

    Підставляємо обчислені значення в стандартну форму\(\ \frac{(x-h)^{2}}{a}-\frac{(y-k)^{2}}{b}=1\), щоб отримати\(\ \frac{(x+1)^{2}}{16}-\frac{y^{2}}{9}=1\).

    Рецензія

    Знайдіть рівняння асимптотів кожної гіперболи.

    1. \(\ \frac{(y+3)^{2}}{4}-(x-2)^{2}=1\)
    2. \(\ \frac{y^{2}}{16}-(x+3)^{2}=1\)
    3. \(\ \frac{(x+2)^{2}}{4}-\frac{(y+1)^{2}}{9}=1\)
    4. \(\ \frac{(y-4)^{2}}{16}-\frac{(x-4)^{2}}{16}=1\)
    5. \(\ \frac{(x-1)^{2}}{1}-\frac{9(y+4)^{2}}{1}=9\)
    6. \(\ \frac{(y+2)^{2}}{16}-\frac{(x-2)^{2}}{1}=1\)
    7. \(\ \frac{(x-4)^{2}}{1}-\frac{(y+1)^{2}}{4}=1\)
    8. \(\ \frac{y^{2}}{16}-\frac{(x+1)^{2}}{4}=1\)
    9. \(\ \frac{(x-3)^{2}}{4}-\frac{(y-4)^{2}}{1}=1\)
    10. \(\ \frac{(x-4)^{2}}{4}-\frac{(y-3)^{2}}{1}=1\)

    Графік гіперболи, дайте рівняння асимптотів і використовуйте асимптоти для підвищення точності вашого графіка.

    1. \(\ \frac{(x+4)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
    2. \(\ \frac{(y+3)^{2}}{4}-\frac{(x-4)^{2}}{9}=1\)
    3. \(\ \frac{(y+4)^{2}}{16}-\frac{(x-1)^{2}}{4}=1\)
    4. \(\ (x-2)^{2}-4 y^{2}=16\)
    5. \(\ \frac{y^{2}}{4}-\frac{(x-1)^{2}}{4}=1\)
    6. \(\ \frac{(x-2)^{2}}{16}-\frac{(y+4)^{2}}{1}=1\)
    7. \(\ \frac{(x+2)^{2}}{9}-\frac{(y+2)^{2}}{16}=1\)
    8. \(\ \frac{(x+4)^{2}}{9}-\frac{(y-2)^{2}}{4}=1\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 6.7.

    Лексика

    Термін Визначення
    Асимптоти Асимптота - це рядок на графіку функції, що представляє значення, до якого функція може наблизитися, але не досягати (за деякими винятками).
    Конічна Конічні перерізи - це ті криві, які можуть бути створені перетином подвійного конуса і площини. Вони включають кола, еліпси, параболи та гіперболи.
    гіпербола Гіпербола - це конічний переріз, утворений, коли січна площина перетинає обидві сторони конуса, в результаті чого утворюються дві нескінченні «U» -образні криві.
    Парабола Парабола - це множина точок, що знаходяться на рівній відстані від фіксованої точки внутрішньої кривої, яка називається «'focus"', і лінія на зовнішній стороні, яка називається «'directrix"'. Директриса буває вертикальною або горизонтальною, в залежності від орієнтації параболи.
    перпендикулярна гіпербола Перпендикулярна гіпербола має асимптоти, які перетинаються під кутом 90.
    необмежений Бути необмеженим означає бути настільки великим, що жодне коло, яким би великим не було, не може обкласти фігуру.