6.3.3: Гіперболи з будь-яким центром

Гіперболи по центру в (h, k)

Ваше домашнє завдання полягає в тому, щоб графувати гіперболу\(\ 9(y+2)^{2}-4(x-3)^{2}=36\). Які вершини вашого графа?

---

Гіперболи по центру в (h, k)

Так само, як ви вже дізналися раніше, гіперболу не завжди потрібно розміщувати з центром біля початку. Якщо центром є\(\ (h,k)\) весь еліпс, будуть зміщені\(\ h\) одиниці вліво або вправо і\(\ k\) одиниці вгору або вниз. Рівняння стає\(\ \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\). Ми розглянемо, як змінюються вершини, співвершини та фокуси у наступній задачі.

Давайте графуємо\(\ \frac{(x-2)^{2}}{16}-\frac{(y+1)^{2}}{9}=1\). Тоді давайте знайдемо вершини, вогнища та асимптоти.

По-перше, ми знаємо, що це горизонтальна гіпербола, оскільки\(\ x\) термін перший. Тому центром є\(\ (2,−1)\) і\(\ a=4\) і\(\ b=3\). Використовуйте цю інформацію для графування гіперболи.

Для графіка побудуйте центр, а потім вийдіть 4 одиниці вправо і вліво, а потім вгору і вниз 3 одиниці. Намалюйте коробку і асимптоти.

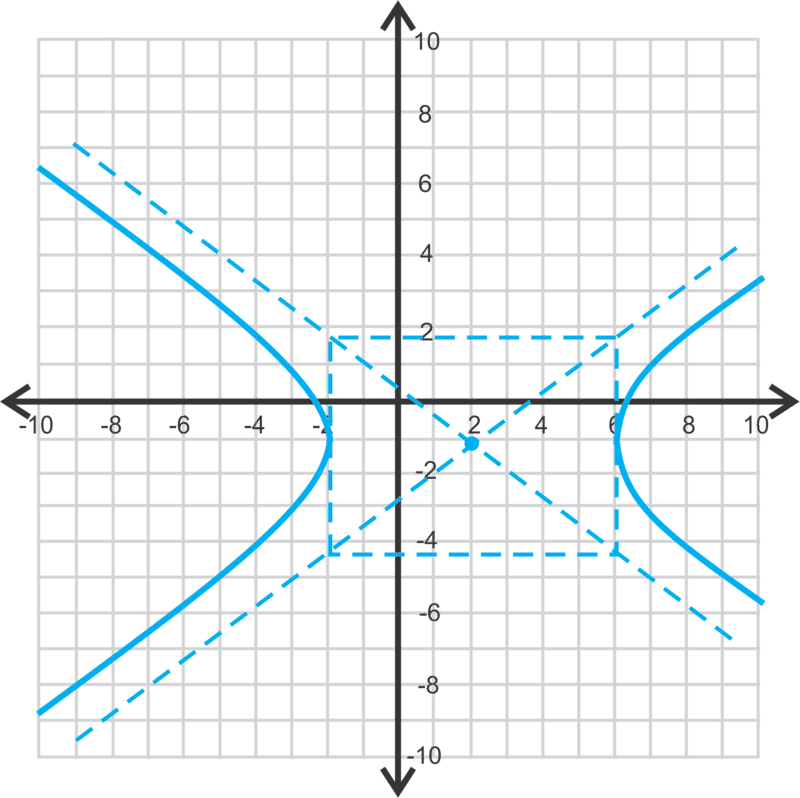
Це також, як ви можете знайти вершини. Вершини є\(\ (2 \pm 4,-1)\) або\(\ (6,-1)\) і\(\ (-2,-1)\).

Щоб знайти осередки, нам потрібно знайти\(\ c\) за допомогою\(\ c^{2}=a^{2}+b^{2}\).

\ (\\ begin {масив} {l}
c^ {2} &=16+9=25\\
c&=5
\ end {масив}\)

Тому осередками є\(\ (2 \pm 5,-1)\) або\(\ (7,−1)\) і\(\ (−3,−1)\).

Щоб знайти асимптоти, нам доведеться трохи попрацювати, щоб знайти y-перехоплення. Ми знаємо, що схил є\(\ \pm \frac{b}{a}\) або\(\ \pm \frac{3}{4}\) і вони проходять через центр. Давайте запишемо кожну асимптоту в точковій формі нахилу, використовуючи центр і кожен нахил.

\(\ y-1=\frac{3}{4}(x+2)\)і\(\ y-1=-\frac{3}{4}(x+2)\)

Спрощуючи кожне рівняння, асимптоти є\(\ y=\frac{3}{4} x-\frac{5}{2}\) і\(\ y=-\frac{3}{4} x+\frac{1}{2}\).

З цієї задачі ми можемо створити формули для знаходження вершин, вогнищ та асимптотів гіперболи з центром\(\ (h,k)\). Крім того, графуючи гіперболу, не зосереджену на початку, переконайтеся, що розмістіть центр.

Орієнтація	Рівняння	Вершини	вогнища	Асимптоти
Горизонтальний	\(\ \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\)	\(\ (h \pm a, k)\)	\(\ (h \pm c, k)\)	\(\ y-k=\pm \frac{b}{a}(x-h)\)
Вертикальний	\(\ \frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1\)	\(\ (h, k \pm a)\)	\(\ (h, k \pm c)\)	\(\ y-k=\pm \frac{a}{b}(x-h)\)

Тепер знайдемо рівняння гіперболи з вершинами\(\ (−3,2)\)\(\ (7,2)\) і фокусом\(\ (−5,2)\).

Ці дві вершини створюють горизонтальну поперечну вісь, роблячи гіперболу горизонтальною. Якщо ви не впевнені, наведіть вказану інформацію на набір осей. Щоб знайти центр, скористайтеся формулою середньої точки з вершинами.

\(\ \left(\frac{-3+7}{2}, \frac{2+2}{2}\right)=\left(\frac{4}{2}, \frac{4}{2}\right)=(2,2)\)

Відстань від однієї з вершин до центру дорівнює\(\ a,|7-2|=5\). Відстань від центру до заданого фокусу дорівнює\(\ c,|-5-2|=7\). \(\ c\)Використовувати\(\ a\) і вирішувати для\(\ b\).

\ (\\ почати {масив} {l}
7^ {2} =5^ {2} +b^ {2}\\
b^ {2} =24\ стрілка вправо b = 2\ sqrt {6}
\ кінець {масив}\)

Тому рівняння є\(\ \frac{(x-2)^{2}}{25}-\frac{(y-2)^{2}}{24}=1\).

Нарешті, давайте проведемо графік\(\ 49(y-3)^{2}-25(x+4)^{2}=1225\) і знайдемо вогнища.

Спочатку ми повинні отримати рівняння в стандартній формі, як і рівняння вище. Щоб зробити праву сторону 1, нам потрібно розділити все на 1225.

\ (\\ почати {масив} {c}
\ розриву {49 (y-3) ^ {2}} {1225} -\ гідророзриву {25 (x+4) ^ {2}} {1225} =\ розриву {1225} {1225}\
\ гідророзриву {(y-3) ^ {2}} {25} -\ гідророзриву {(x+4) ^ {2} {49}} =1
\ end {масив}\)

Тепер ми знаємо, що гіпербола буде вертикальною, оскільки y-термін є першим.

\(\ a=5\),\(\ b=7\) а центр є\(\ (−4,3)\).

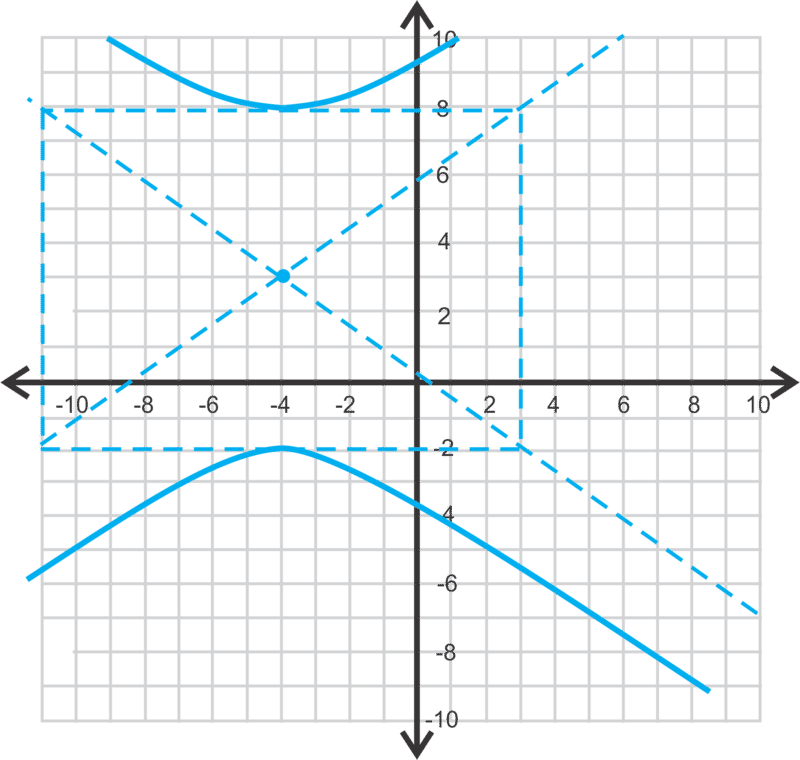
Щоб знайти вогнища, нам спочатку потрібно знайти\(\ c\) за допомогою\(\ c^{2}=a^{2}+b^{2}\).

\ (\\ почати {вирівняний}
c^ {2} &=49+25=74\\
c &=\ sqrt {74}
\ кінець {вирівняний}\)

Вогнищами є\(\ (-4,3 \pm \sqrt{74})\) або\(\ (−4,11.6)\) і\(\ (−4,−5.6)\).

---

Приклади

Приклад 1

Раніше вам було запропоновано визначити вершини графа гіперболи, визначеної\(\ 9(y+2)^{2}-4(x-3)^{2}=36\).

Рішення

Спочатку нам потрібно отримати рівняння в стандартному вигляді\(\ \frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1\), тому ділимо на\(\ 36\).

\ (\\ почати {масив} {r}
9 (y+2) ^ {2} -4 (x-3) ^ {2} =&36\
\ розриву {9 (y+2) ^ {2}} {36} -\ розриву {4 (x-3) ^ {2}} {36} =&\ гідророзриву {36} {36} {36}\
\ frac {(y+2) ^ {2}} {4} -\ гідророзриву {(x-3) ^ {2}} {9} =&1
\ end {масив}\)

Тому що y -термін є першим, тепер ми можемо бачити, що вершини є\(\ (h, k \pm a)(3,-2 \pm 2)\). Тобто,\(\ (3,0)\) і\(\ (3,−4)\)

Приклад 2

Знайдіть центр, вершини, вогнища та асимптоти\(\ \frac{(y-1)^{2}}{81}-\frac{(x+5)^{2}}{16}=1\).

Рішення

Центр є\(\ (−5,1)\),\(\ a=\sqrt{81}=9\) і\(\ b=\sqrt{16}=4\), і гіпербола горизонтальна, тому що y-термін є першим. Вершини є\(\ (-5,1 \pm 9)\) або\(\ (-5,10)\) і\(\ (−5,−8)\). Використовуйте\(\ c^{2}=a^{2}+b^{2}\) для пошуку\(\ c\).

\ (\\ почати {вирівняний}
c^ {2} &=81+16 = 97\\
c &=\ sqrt {97}
\ кінець {вирівняний}\)

Вогнищами є\(\ (-5,1+\sqrt{97})\) і\(\ (-5,1-\sqrt{97})\).

Асимптотами є\(\ y-1=\pm \frac{9}{4}(x+5)\) або\(\ y=\frac{9}{4} x+12 \frac{1}{4}\) і\(\ y=-\frac{9}{4} x-10 \frac{1}{4}\).

Приклад 3

Графік\(\ 25(x-3)^{2}-4(y-1)^{2}=100\) і знайдіть осередки.

Рішення

Змініть це рівняння на стандартну форму для того, щоб зробити графік.

\ (\\ почати {масив} {l}
\ гідророзриву {25 (x-3) ^ {2}} {100} -\ гідророзриву {4 (y-1) ^ {2}} {100} {100} {100}\
\ гідророзриву {(x-3) ^ {2}} {4} -\ гідророзриву {(y-1) ^ {2}} {25} &=1
\ end {масив}\)

центр:\(\ (3,1), a=2, b=5\)

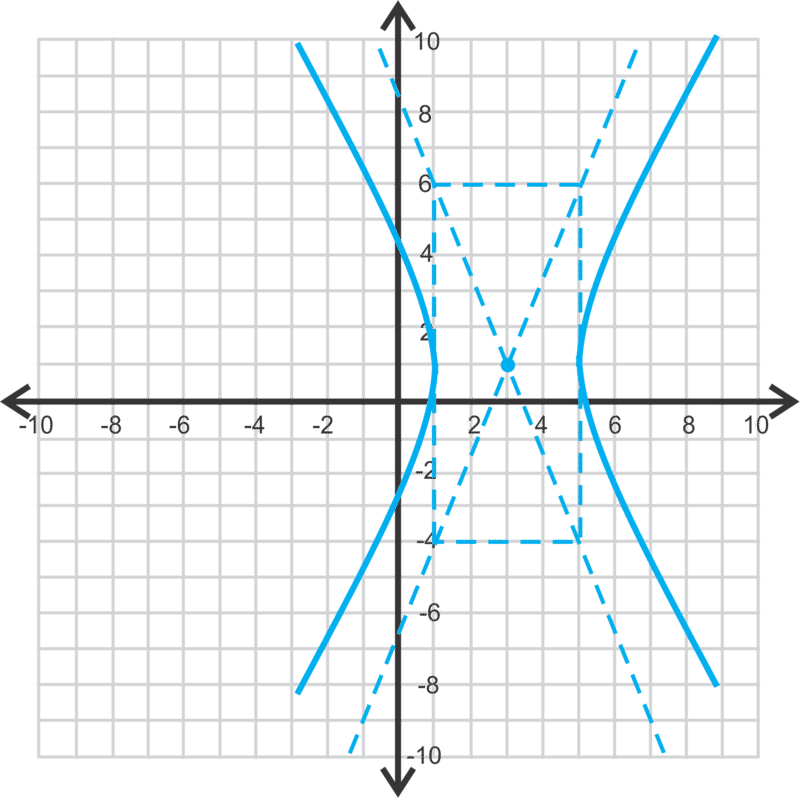
Знайдіть вогнища.

\ (\\ почати {масив} {l}
c^ {2} &=25+4=29\\
c&=\ sqrt {29}
\ кінець {масив}\)

Вогнищами є\(\ (3,1+\sqrt{29})\) і\(\ (3,1-\sqrt{29})\).

Приклад 4

Знайдіть рівняння гіперболи з вершинами\(\ (−6,−3)\)\(\ (−6,5)\) і фокусом\(\ (−6,7)\).

Рішення

Вершини є\(\ (−6,−3)\) і,\(\ (−6,5)\) і фокус є\(\ (−6,7)\). Поперечна вісь буде вертикальною, оскільки значення x не змінюється між цими трьома точками. Відстань між вершинами -\(\ |-3-5|=8\) одиниці, що роблять\(\ a=4\). Серединою між вершинами є центр.

\(\ \left(-6, \frac{-3+5}{2}\right)=\left(-6, \frac{2}{2}\right)=(-6,1)\)

Фокус є\(\ (−6,7)\) і відстань між ним і центром становить 6 одиниць, або\(\ c\). Знайти\(\ b\).

\ (\\ почати {вирівняний}
36 &=b^ {2} +16\\
20 &=b^ {2}\\
b &=\ sqrt {20} =2\ sqrt {5}
\ кінець {вирівняний}\)

Рівняння гіперболи є\(\ \frac{(y-1)^{2}}{16}-\frac{(x+6)^{2}}{20}=1\).

---

Рецензія

Знайдіть центр, вершини, вогнища та асимптоти кожної гіперболи нижче.

1. \(\ \frac{(x+5)^{2}}{25}-\frac{(y+1)^{2}}{36}=1\)
2. \(\ (y+2)^{2}-16(x-6)^{2}=16\)
3. \(\ \frac{(y-2)^{2}}{9}-\frac{(x-3)^{2}}{49}=1\)
4. \(\ 25 x^{2}-64(y-6)^{2}=1600\)
5. \(\ (x-8)^{2}-\frac{(y-4)^{2}}{9}=1\)
6. \(\ 81(y+4)^{2}-4(x+5)^{2}=324\)
7. Графік гіперболи в #1.
8. Графік гіперболи в #2.
9. Графік гіперболи в #5.
10. Графік гіперболи в #6.

Використовуючи наведену нижче інформацію, знайдіть рівняння кожної гіперболи.

11. вершини:\(\ (−2,−3)\) і\(\ (8,−3)b=7\)
12. вершини:\(\ (5,6)\) і\(\ (5,−12)\) фокус:\(\ (5,−15)\)
13. асимптота:\(\ y+3=\frac{4}{9}(x+1)\) горизонтальна поперечна вісь
14. вогнища:\(\ (−11,−4)\) і\(\ (1,−4)\) вершинні:\(\ (−8,−4)\)
15. Розширення Перепишіть рівняння гіперболи,
16. \(\ x^{2}-4 y^{2}+490 x-16 y+1013=0\)в стандартній формі, заповнивши квадрат для обох\(\ x\) і\(\ y\) термінів.

---

Відповіді на проблеми з оглядом

Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 10.9.

---

Атрибуції зображень

1. [Малюнок 1]
   Кредит: Бен Солтер
   Джерело: https://www.flickr.com/photos/ben_salter/2348052408