Skip to main content
LibreTexts - Ukrayinska

4.5.3: Квадратична формула та комплексні суми

  1. Last updated
  2. Save as PDF
  • Page ID
    54966

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Комплексні корені квадратичних функцій

    Квадратична функція\(\ y=x^{2}-2 x+3\) (показано нижче) не перетинає вісь x і тому не має реальних коренів. Які складні коріння функції?

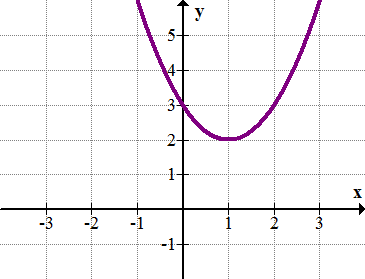
    F-д_А9362114ЕД 79659С0Б67А 36746 ЕФБ0Д37ЕЕ4ФФ 4Е9Б4817472Д1С013+зображення_крихіткий+зображення_крихіткий.PNG

    Комплексні корені квадратичних функцій

    Нагадаємо, що уявне число\(\ i\), - це число, квадрат якого дорівнює —1:

    \(\ \color{red}i^{2}=-1\)і\(\ \color{red}i=\sqrt{-1}\)

    Сума дійсного числа і уявного числа називається комплексним числом. Прикладами комплексних чисел є\(\ 5+4i\) і\(\ 3−2i\). Всі комплексні числа можна записати у вигляді\(\ a+bi\) де\(\ a\) і\(\ b\) є дійсними числами. Два важливих моменти:

    • Множина дійсних чисел є підмножиною множини комплексних чисел де\(\ b=0\).

      Прикладами дійсних чисел є\(\ 2,7, \frac{1}{2},-4.2\).

    • Безліч уявних чисел є підмножиною множини комплексних чисел де\(\ a=0\).

      Прикладами уявних чисел є\(\ i,-4 i, \sqrt{2} i\).

    Це означає, що набір комплексних чисел включає дійсні числа, уявні числа, а також комбінації дійсних і уявних чисел.

    Коли квадратична функція не перетинає вісь x, вона має складні коріння. При вирішенні для коренів функції алгебраїчно за допомогою квадратичної формули ви отримаєте негативний під символом квадратного кореня. З вашим знанням комплексних чисел, ви все ще можете вказати складні коріння функції так само, як ви б стверджували реальні корені функції.

    Розв'яжемо квадратне рівняння: m 2 −2m+5=0

    Для вирішення можна використовувати квадратичну формулу. Для цього квадратного рівняння,\(\ a=1, b=−2, c=5\).

    \ (\\ почати {вирівняний}
    м &=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\
    m &=\ frac {- ({\ колір {червоний} -2})\ pm\ sqrt {({колір {червоний} -2}) ^ {2} -4 ({колір {червоний} 1}) ({\ колір {червоний}} 5})}} {2 ({\ колір {червоний} 1})}\\
    m &=\ frac {2\ pm\ sqrt {4-20}} {2}\\
    m &=\ frac {2\ pm\ sqrt {-16}} {2}\ quad\ quad\ quad\ quad\ quad\ sqrt {-16} =\ sqrt {16}\ раз i = 4 i\\
    m &=\ frac {2\
    pm 4 i} {2}\\ m &= 1\\
    m &=1+2 i\ текст {або} m = 1-2 i
    \ кінець {вирівняний}\)

    Реальних розв'язків рівняння немає. Розв'язки квадратного рівняння є\(\ 1+2 i \text { and } 1-2 i\).

    Тепер давайте вирішимо наступне рівняння, переписуючи його як квадратичне і використовуючи квадратичну формулу:

    \(\ \frac{3}{e+3}-\frac{2}{e+2}=1\)

    Щоб переписати як квадратне рівняння, помножте кожен член на\(\ (e+3)(e+2)\).

    \ (\\ begin {масив} {l}
    \ frac {3} {e+3} {\ колір {червоний} (e+3) (e+2)} -\ frac {2} {e+2} {\ колір {червоний} (e+2)} {\ колір {червоний} (e+3)}\ 3 (e+2) -2 (
    e+3) =( e+3) =( e+3) +3) (e+2)
    \ end {масив}\)

    Розширюйте і спрощуйте.

    \ (\\ begin {масив} {l}
    3 e+6-2 e-6=e^ {2} +2 e+3 e+6\
    e^ {2} +4 e+6 = 0
    \ end {масив}\)

    Вирішіть за допомогою квадратичної формули. Для цього квадратного рівняння,\(\ a=1, b=4, c=6\).

    \ (\\ begin {масив} {l}
    e=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\
    e=\ frac {- ({\ колір {червоний} {\ колір {червоний} 4}) ^ {2} -4 ({\ колір {червоний} 1}) {\ колір {червоний} 6})}} {2 ({\ колір {червоний} 1})}\\
    e=\ frac {-4\ pm\ sqrt {16-24}} {2}\\
    e=\ frac {-4\ pm\ sqrt {-8}} {2}\ quad\ квад\ квад\ квад\ sqrt {-8} =\ sqrt {8}\ раз i =\ sqrt {4\ cdot 2}\ раз i\
    sqrt {2}\\ sqrt {2}\ sqrt {2}\\
    cdot 2\ pm i\ sqrt {2}\
    sqrt {2} 2}\ текст {або} e=-2-i\ sqrt {2}
    \ end {масив}\)

    Реальних розв'язків рівняння немає. Розв'язками рівняння є

    \(\ -2+i \sqrt{2} \text { and }-2-i \sqrt{2}\)

    Нарешті, давайте намалюємо графік наступної квадратичної функції. Які коріння цієї функції?

    \(\ y=x^{2}-4 x+5\)

    Скористайтеся калькулятором або таблицею, щоб зробити ескіз функції. У вас повинно вийти наступне:

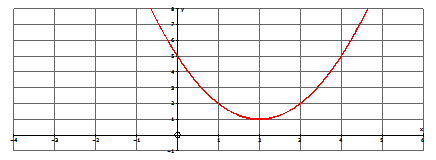
    Ф-Д_САА 4А 3888 Е16Ф0БФ6Д022408696 ЕБ42К4Ф9613ББ6Б03ФД468А1213Ф4+зображення_крихіткий+зображення_крихіткий.PNG

    Як бачите, квадратична функція не має x-перехоплень, отже, функція не має реальних коренів. Щоб знайти коріння (які будуть складними), необхідно використовувати квадратичну формулу.

    Для цієї квадратичної функції,\(\ a=1, b=-4, c=5\).

    \ (\\ begin {масив} {l}
    x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\
    x =\ frac {- ({\ колір {червоний} -4})\ pm\ sqrt {({\ колір {червоний} -4}) ^ {2} -4 ({колір {червоний} 1}) ({\ колір {колір {колір {колір {колір {червоний} 5})}} {2 ({\ колір {червоний} 1})}\\
    x=\ frac {4\ pm\ sqrt {16-20}} {2}\\
    x=\ frac {4\ pm\ sqrt {-4}} {2}\ квад\ quad\ квад\ квад\ sqrt {-4} =\ sqrt {4}\ раз i = 2 i\\
    x =\ frac {4\ pm 2 i} {2}\
    x = 2\ pm i\
    x = 2+i\ text {або} x = 2-i
    \ end {масив}\)

    Складні коріння квадратичної функції є\(\ 2+i \text { and } 2-i\).

    Приклади

    Приклад 1

    Раніше вас попросили знайти складні коріння\(\ y=x^{2}-2 x+3\).

    Рішення

    Щоб знайти складні корені функції\(\ y=x^{2}-2 x+3\), необхідно використовувати квадратичну формулу.

    Для цієї квадратичної функції,\(\ a=1, b=-2, c=3\).

    \ (\\ begin {масив} {l}
    x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\
    x =\ frac {- ({\ колір {червоний} -2})\ pm\ sqrt {({\ колір {червоний} -2}) ^ {2} -4 ({колір {червоний} 1}) ({\ колір {колір {колір {колір {червоний} 1} червоний} 3})}} {2 ({\ color {червоний} 1})}\\
    x=\ frac {2\ pm\ sqrt {4-12}} {2}\\
    x=\ frac {2\ pm\ sqrt {-8}} {2}\ квад\ quad\ квадрат\ sqrt {-8} =\ sqrt {8}\ раз i=2\ sqrt {2} я\\
    x=\ frac {2\ pm 2\ sqrt {2} i} {2}\
    x = 1\ pm\ sqrt {2} i
    \ end {масив}\)

    Приклад 2

    Розв'яжіть наступне квадратне рівняння. Висловлюйте всі рішення в найпростішій радикальній формі.

    \(\ 2 n^{2}+n=-4\)

    Рішення

    Встановіть рівняння рівне нулю.

    \(\ 2 n^{2}+n+4=0\)

    Вирішіть за допомогою квадратичної формули.

    \ (\\ почати {масив} {л}
    x=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\
    n=\ frac {- ({\ колір {червоний} 1})\ pm\ sqrt {({\ колір {червоний} 1}) ^ {2} -4 ({колір {червоний} 2}) ({\ колір {колір {колір {червоний} 2} червоний} 4})}} {2 ({\ колір {червоний} 2})}\\
    n=\ frac {-1\ pm\ sqrt {1-32}} {4}\\
    n=\ frac {-1\ pm\ sqrt {-31}} {4}\\
    n=\ frac {-1\ пм я\ sqrt {31}} {4}
    \ кінець {масив}\)

    Приклад\(\PageIndex{1}\)

    Розв'яжіть наступне квадратне рівняння. Висловлюйте всі рішення в найпростішій радикальній формі.

    \(\ m^{2}+(m+1)^{2}+(m+2)^{2}=-1\)

    Рішення

    Розширюйте і спрощуйте.

    \ (\\ почати {масив} {l}
    m^ {2} + (м+1) (м+1) + (м+2) (м+2) =-1\
    m^ {2} +м^ {2} +м+1+м^ {2} +2 м+2 м+4 = -1\\
    3 м^ {2} +6 м+5 = -1
    \ кінець {масив}\)

    Запишіть рівняння в загальному вигляді.

    \(\ 3 m^{2}+6 m+6=0\)

    Розділіть на 3, щоб спростити рівняння.

    \ (\\ begin {масив} {l}
    \ frac {3 m^ {2}} {\ колір {червоний} 3} +\ frac {6 м} {\ колір {червоний} 3} +\ frac {6} {\ колір {червоний} 3} =\ frac {0} {\ колір {червоний} 3}\\
    m^ {2} +2 m+2 = 0
    \ кінець {масив})

    Вирішіть за допомогою квадратичної формули:

    \ (\\ почати {масив} {l}
    m=\ frac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\
    m=\ frac {- ({\ колір {червоний} 2})\ pm\ sqrt {({\ колір {червоний} 2}) ^ {2} -4 ({колір {червоний} 1}) ({\ колір {колір {колір {колір {колір {колір {колір} 1} червоний} 2})}} {2 ({\ колір {червоний} 1})}\\
    m=\ frac {-2\ pm\ sqrt {4-8}} {2}\\
    m=\ frac {-2\ pm\ sqrt {-4}} {2}\\
    m=\ гідророзриву {-2\ пм 2 я} {2}\\
    м = -1\ pm i
    \ end {масив}\)

    Приклад 4

    Чи можливо, щоб квадратична функція мала рівно один складний корінь?

    Рішення

    Ні, навіть у поліномах вищого ступеня складні коріння завжди будуть приходити парами. Розглянемо, коли ви використовуєте квадратичну formula— якщо у вас є негативний під символом квадратного кореня, як версія +, так і - версія двох відповідей в кінцевому підсумку будуть складними.

    Рецензія

    1. Якщо квадратична функція має 2 x-перехоплення, скільки складних коренів вона має? Поясніть.
    2. Якщо квадратична функція не має x-перехоплень, скільки складних коренів вона має? Поясніть.
    3. Якщо квадратична функція має 1 x-перехоплення, скільки складних коренів вона має? Поясніть.
    4. Якщо ви хочете знати, чи має функція складні корені, на якій частині квадратичної формули важливо зосередитися?
    5. Ви вирішуєте квадратне рівняння і отримуєте 2 комплексних рішення. Як ви можете перевірити свої рішення?
    6. Загалом, ви можете спробувати вирішити квадратне рівняння за допомогою графіків, факторингу, заповнення квадрата або за допомогою квадратної формули. Якщо квадратне рівняння має складні розв'язки, які методи ви маєте для вирішення рівняння?

    Розв'яжіть наступні квадратні рівняння. Висловлюйте всі рішення в найпростішій радикальній формі.

    1. \(\ x^{2}+x+1=0\)
    2. \(\ 5 y^{2}-8 y=-6\)
    3. \(\ 2 m^{2}-12 m+19=0\)
    4. \(\ -3 x^{2}-2 x=2\)
    5. \(\ 2 x^{2}+4 x=-11\)
    6. \(\ -x^{2}+x-23=0\)
    7. \(\ -3 x^{2}+2 x=14\)
    8. \(\ x^{2}+5=-x\)
    9. \(\ \frac{1}{2} d^{2}+4 d=-12\)

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 9.7.

    Лексика

    Термін Визначення
    комплексне число Комплексне число - це сума дійсного числа і уявного числа, записаного у вигляді\(\ a+bi\).
    складний корінь Комплексний корінь - це комплексне число, яке при використанні в якості вхідного (\(\ x\)) значення функції призводить до вихідного (\(\ y\)) значення нуля.
    уявні числа Уявне число - це число, яке можна записати як добуток дійсного числа і i.
    Квадратична формула У квадратичній формулі зазначено, що для будь-якого квадратного рівняння у вигляді\(\ a x^{2}+b x+c=0, x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\).
    Реальне число Реальне число - це число, яке може бути нанесено на числовий рядок. Справжні числа включають в себе всі раціональні та ірраціональні числа.