Skip to main content
LibreTexts - Ukrayinska

4.5.2: Комплексні числа

  1. CK-12 License
  2. Last updated
    Oct 27, 2022
  3. Save as PDF

Визначення комплексних чисел

Найхолодніша можлива температура, відома як абсолютний нуль, становить майже -460 градусів за Фаренгейтом. Що таке квадратний корінь цього числа?

Комплексні числа

До цього поняття всі числа були дійсними числами.  2,−5,√11, і 13 всі приклади дійсних чисел. З тим, що ми раніше дізналися, ми не можемо знайти, √−25 тому що ви не можете взяти квадратний корінь негативного числа. Немає дійсного числа, яке при множенні на себе дорівнює -25. Давайте спростимо √−25.

 √−25=√25⋅−1=5√−1

Для того, щоб взяти квадратний корінь від'ємного числа, ми збираємося призначити √−1 змінну, i.i являє собою уявне число. Тепер ми можемо використовувати i, щоб взяти квадратний корінь від'ємного числа.

 √−25=√25⋅−1=5√−1=5i

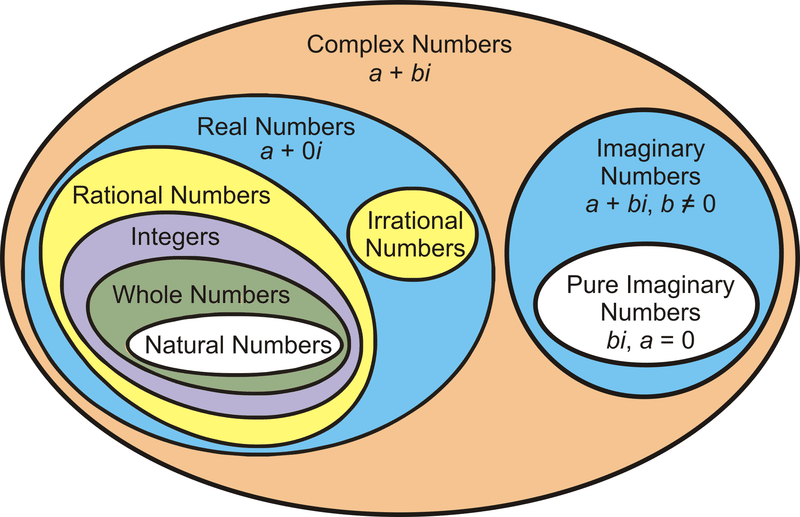
Всі комплексні числа мають вигляд a+bi, де a і b - дійсні числа. a - дійсна частина комплексного числа, а b - уявна частина. Якщо b=0, то ліворуч a, а число - дійсне число. Якщо a=0, то число тільки bi і називається чистим уявним числом. Якщо b0 і a0, то число буде уявним числом.

Ф-д_1д89ф018а 4Б787818Д4Ф67Е1 ЕАЕ30ЕД 96165 ЕСК670ДАД 21ААБ9FF52F+зображення_крихіткий+зображення_крихіткий.PNG[Малюнок 1]

Давайте знайдемо √−162.

Спочатку витягніть i. Потім, спростити √162.

 √−162=√−1⋅√162=i√162=i√81⋅2=9i√2

повноваження i

На додаток до того, що тепер можна взяти квадратний корінь негативного числа, я також має деякі цікаві властивості. Спробуйте знайти i2,i3, and i4.

Крок 1: Випишіть i2 і спростіть.  i2=i⋅i=√−1⋅√−1=√−12=−1

Крок 2: Випишіть i3 і спростіть.  i3=i2⋅i=−1⋅i=−i

Крок 3: Випишіть i4 і спростіть.  i4=i2⋅i2=−1⋅−1=1

Крок 4: Випишіть i5 і спростіть.  i5=i4⋅i=1⋅i=i

Крок 5: Випишіть i6 і спростіть.  i6=i4⋅i2=1⋅−1=−1

Крок 6: Ви бачите візерунок? Опишіть його і спробуйте знайти i19.

Ви повинні бачити, що повноваження i повторюють кожні 4 сили. Отже, всі повноваження, які діляться на 4, дорівнюватимуть 1. Щоб знайти i19, ділимо 19 на 4 і визначаємо залишок. Це підкаже, яка потужність вона така ж, як.

 i19=i16⋅i3=1⋅i3=−i

Тепер, давайте знайдемо наступні повноваження i.

  1.  i32

    32 ділиться на 4, так i32=1.

  2.  i50

    50÷4=12, з залишком 2. Тому, i50=i2=−1.

  3.  i7

    7÷4=1, з залишком 3. Тому, i7=i3=−i

Нарешті, давайте спростимо наступні складні вирази.

  1.  (6−4i)+(5+8i)

     (6−4i)+(5+8i)=6−4i+5+8i=11+4i

  2.  9−(4+i)+(2−7i)

     9−(4+i)+(2−7i)=9−4−i+2−7i=7−8i

Щоб скласти або відняти комплексні числа, потрібно комбінувати подібні терміни. Будьте обережні з негативами і правильно їх розподіляючи. Ваша відповідь завжди повинна бути в стандартній формі, яка є a+bi.

Приклади

Приклад 1

Раніше вас просили знайти квадратний корінь -460 градусів.

Рішення

Ми шукаємо √−460.

Для початку нам потрібно витягнути i. Потім, нам потрібно спростити √460.

 √−460=√−1⋅√460=i√460=i√4⋅115=2i√115

Приклад 2

Спростити √−49.

Рішення

Перепишіть з √−49 точки зору i і спростіть радикальне.

 √−49=i√49=7i

Приклад 3

Спростити √−125.

Рішення

Перепишіть з √−125 точки зору i і спростіть радикальне.

 √−125=i√125=i√25⋅5=5i√5

Приклад 4

Спростити i210.

Рішення

210÷4=52, з залишком 2. Тому, i210=i2=−1.

Приклад 5

Спростити (8−3i)−(12−i).

Рішення

Розподіліть негатив і комбінуйте подібні терміни.

 (8−3i)−(12−i)=8−3i−12+i=−4−2i

Рецензія

Спрощуйте кожен вираз і пишіть в стандартній формі.

  1.  √−9
  2.  √−242
  3.  6√−45
  4.  −12i√98
  5.  √−32⋅√−27
  6.  7i√−126
  7.  i8
  8.  16i22
  9.  −9i65
  10.  i365
  11.  2i91
  12.  √−1680
  13.  (11−5i)+(6−7i)
  14.  (14+2i)−(20+9i)
  15.  (8−i)−(3+4i)+15i
  16.  −10i−(1−4i)
  17.  (0.2+1.5i)−(−0.6+i)
  18.  6+(18−i)−(2+12i)
  19.  −i+(19+22i)−(8−14i)
  20.  18−(4+6i)+(17−9i)+24i

Відповіді на проблеми з оглядом

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 5.8.

Лексика

Термін Визначення
 i  iє уявним числом.  i=√−1.
Абсолютна величина Абсолютне значення числа - це відстань, на якій знаходиться число від нуля. Абсолютна величина комплексного числа - це відстань від комплексного числа на комплексній площині до початку.
Складний кон'югат Складні кон'югати - це пари складних біноміалів. Складний сполучений з a+bi є a−bi. При множенні складних сполучень виходить єдине дійсне число.
я це уявне число.  i=√−1.
Уявне число Уявне число - це число, яке можна записати як добуток дійсного числа і i.
уявна частина Уявна частина комплексного числа a+bi - це bi.
Чисті уявні числа Чисті уявні числа є підмножиною комплексних чисел без дійсних частин, тільки bi.
Реальне число Реальне число - це число, яке може бути нанесено на числовий рядок. Справжні числа включають в себе всі раціональні та ірраціональні числа.
реальна частина Реальна частина комплексного числа a+bi - це a.
прямокутні координати Точка записується за допомогою прямокутних координат, якщо вона записана y термінами x і може бути позначена на декартовій площині.
прямокутна форма Прямокутна форма точки або кривої задається через x і y і зображується на декартовій площині.
стандартна форма Стандартна форма комплексного числа - це a+bi де a і b - дійсні числа.