9.5: Приклади похідних

Last updated
Save as PDF

Page ID: 52890

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Приклад\(\PageIndex{1}\)

Наведемо висновок речення\((A \land B) \lif A\).

Починаємо з написання потрібного висновку внизу деривації.

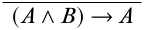
9.5.1.PNG

Далі нам потрібно розібратися, до якого висновку може привести речення такого виду. Основним оператором висновку є\(\lif\), тому спробуємо прийти до висновку за допомогою\(\Intro{\lif}\) правила. Найкраще записати припущення, що беруть участь, і позначити правила висновку, як ви прогресуєте, так що легко побачити, чи всі припущення були виписані в кінці доказу.

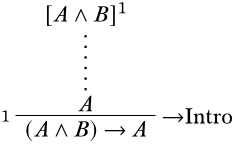
9.5.2.png

Тепер нам потрібно заповнити кроки від припущення\(A \land B\) до\(A\). Оскільки у нас є лише один сполучний, щоб мати справу\(\land\), ми повинні використовувати правило\(\land\) elim. Це дає нам наступний доказ:

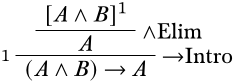
9.5.3.png

Тепер ми маємо правильне виведення\((A \land B) \lif A\).

Приклад\(\PageIndex{2}\)

Тепер давайте наведемо виведення\((\lnot A \lor B) \lif (A \lif B)\).

Починаємо з написання потрібного висновку внизу деривації.

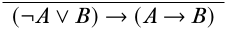
9.5.4.png

Щоб знайти логічне правило, яке могло б дати нам такий висновок, ми розглянемо логічні зв'язки в ув'язненні:\(\lnot\),\(\lor\), і\(\lif\). Ми дбаємо лише на даний момент про перше виникнення\(\lif\) тому, що це головний оператор речення в кінцевому послідовності\(\lnot\),\(\lor\) а друге виникнення\(\lif\) знаходяться всередині сфери дії іншого сполучного, тому ми будемо подбайте про них пізніше. Тому ми починаємо з\(\Intro{\lif}\) правила. Правильне застосування повинно виглядати наступним чином:

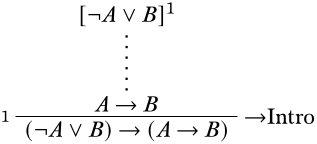
9.5.5.png

Це залишає нам дві можливості продовжувати. Або ми можемо продовжувати працювати знизу вгору і шукати інше застосування\(\Intro{\lif}\) правила, або ми можемо працювати зверху вниз і застосувати\(\Elim{\lor}\) правило. Застосовуємо останні. Ми будемо використовувати припущення\(\lnot A \lor B\) як крайню ліву передумову\(\Elim{\lor}\). Для дійсного застосування\(\Elim{\lor}\), інші два приміщення повинні бути ідентичними висновку\(A \lif B\), але кожне може бути виведено в свою чергу з іншого припущення, а саме двох диз'юнктів\(\lnot A \lor B\). Отже, наша деривація буде виглядати наступним чином:

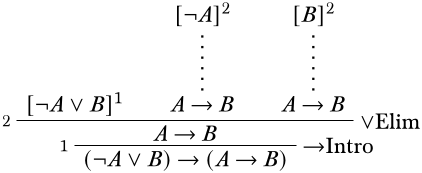
9.5.6.png

У кожній з двох гілок праворуч ми хочемо вивести\(A \lif B\), що найкраще зробити за допомогою\(\Intro{\lif}\).

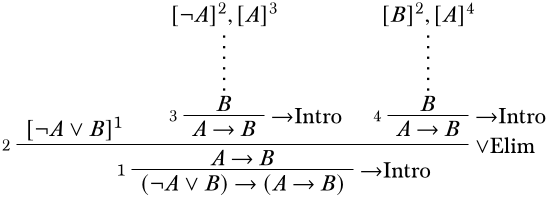
9.5.7.пнг

Для двох відсутніх частин деривації нам потрібні похідні\(B\) від\(\lnot A\) і\(A\) посередині,\(A\) і від і\(B\) зліва. Візьмемо перший перший. \(\lnot A\)і\(A\) є двома приміщеннями\(\Elim{\lnot}\):

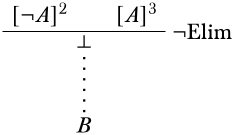
9.5.8.png

Використовуючи\(\FalseInt\), ми можемо отримати\(B\) як висновок, так і завершити гілку.

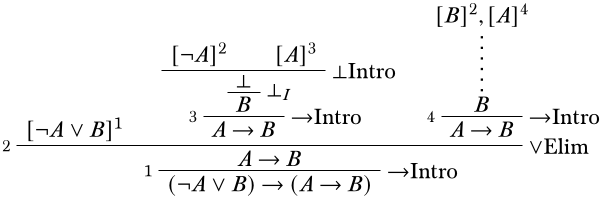
9.5.9.png

Давайте тепер розглянемо крайню праву гілку. Тут важливо усвідомлювати, що визначення деривації дозволяє виписувати припущення, але не вимагає їх. Іншими словами, якщо ми можемо виходити\(B\) з одного з припущень\(A\) і\(B\) без використання іншого, це нормально. А виходити\(B\) з\(B\) банально: саме\(B\) по собі таке похідне, і ніяких висновків не потрібно. Таким чином, ми можемо просто видалити припущення\(A\).

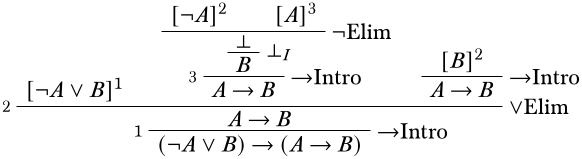
9.5.10.пнг

Зверніть увагу, що в готовій деривації крайній\(\Intro{\lif}\) правий висновок фактично не виконує жодних припущень.

Приклад\(\PageIndex{3}\)

Поки що нам не потрібне\(\FalseCl{}\) правило. Він особливий тим, що дозволяє нам виконати припущення, яке не є підформулою висновку правила. Це тісно пов'язане з\(\FalseInt{}\) правилом. Насправді\(\FalseInt{}\) правило є окремим випадком\(\FalseCl{}\) правила - існує логіка, яка називається «інтуїціоністична логіка», в якій\(\FalseInt{}\) дозволено лише. \(\FalseCl{}\)Правило - крайній засіб, коли більше нічого не працює. Наприклад, припустимо, що ми хочемо отримати\(A \lor \lnot A\). Наша звичайна стратегія полягала б у спробі отримати\(A \lor \lnot A\) використання\(\Intro{\lor}\). Але це вимагатиме від нас виходити\(A\) або\(\lnot A\) з жодних припущень, і цього не можна зробити. \(\FalseCl{}\)на допомогу!

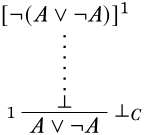
9.5.11.пнг

Тепер ми шукаємо похідний\(\lfalse\) від\(\lnot(A \lor \lnot A)\). Оскільки\(\lfalse\) висновок\(\Elim{\lnot}\) ми можемо спробувати, що:

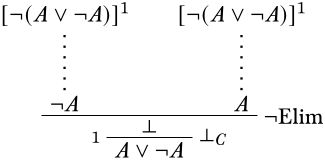
9.5.12.пнг

Наша стратегія пошуку деривації\(\lnot A\) закликів для застосування\(\Intro{\lnot}\):

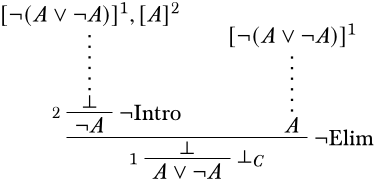
9.5.13 пнг

Тут ми можемо\(\lfalse\) легко отримати, застосувавши\(\Elim{\lnot}\) до припущення,\(\lnot(A \lor \lnot A)\) і\(A \lor \lnot A\) що випливає з нашого нового припущення\(A\)\(\Intro{\lor}\):

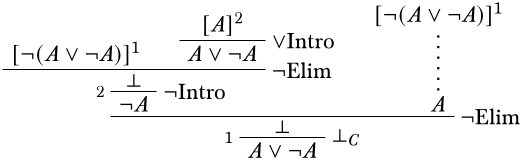
9.5.14.пнг

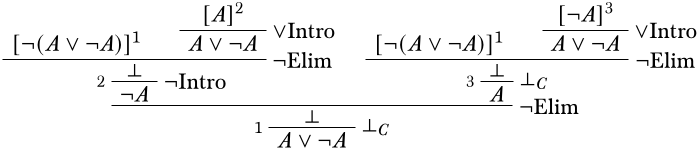
З правого боку ми використовуємо ту ж стратегію, за винятком того, що ми\(A\) отримуємо\(\FalseCl\):

9.5.15 пнг

Проблема\(\PageIndex{1}\)

Дайте похідні такі:

\(\lnot(A \lif B) \lif (A \land \lnot B)\)
\((A \lif C) \lor (B \lif C)\)з припущення\((A \land B) \lif C\)
\(\lnot \lnot A \lif A\)
\(\lnot A \lif \lnot B\)з припущення\(B \lif A\)
\(\lnot A\)з припущення\(( A \lif \lnot A )\)
\(A\)з припущень\(B \lif A\) і\(\lnot B \lif A\)