Skip to main content
LibreTexts - Ukrayinska

8.13: Похідні з присудком ідентичності

  1. Last updated
  2. Save as PDF
  • Page ID
    52971

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Template:MathJaxZach

    Похідні з присудком ідентичності вимагають додаткових початкових послідовностей і правил висновку.

    Визначення\(\PageIndex{1}\): Initial sequents for \(\eq[][]\)

    Якщо\(t\) є закритим терміном, то\({} \Sequent \eq[t][t]\) є початковою послідовністю.

    Правила для\(\eq[][]\) є (\(t_1\)і\(t_2\) є закритими термінами):

    8.13.1.png

    Приклад\(\PageIndex{1}\)

    Якщо\(s\) і\(t\) є закритими термінами, то\(\eq[s][t], A(s) \Proves A(t)\):

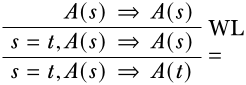
    8.13.2.png

    Це може бути знайомим як принцип замінності ідентиків, або Закон Лейбніца.

    \(\Log{LK}\)доводить, що\(\eq[][]\) є симетричним і перехідним:

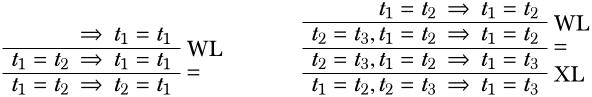
    8.13.3.png

    У доказі зліва формула\(\eq[x][t_1]\) наша\(A(x)\). Справа беремо\(A(x)\) бути\(\eq[t_1][x]\).

    Проблема\(\PageIndex{1}\)

    Наведіть похідні наступних послідовностей:

    1. \(\Sequent \lforall{x}{\lforall{y}{((x = y \land A(x)) \lif A(y))}}\)

    2. \(\lexists{x}{A(x)} \land \lforall{y}{\lforall{z}{((A(y) \land A(z)) \lif y = z)}} \Sequent \lexists{x}{(A(x) \land \lforall{y}{(A(y) \lif y = x)})}\)