3: Структура населення та кореляції між локусами
- Page ID
- 7844
Особи рідко спаровуються абсолютно випадково, ваші батьки не були двома Білатеріями, вирваними навмання з дерева життя. Навіть у межах видів часто існує географічно обмежене спаровування серед особин. Особи, як правило, спаровуються з особами з однакових або тісно пов'язаних сукупностей популяцій. Ця форма невипадкового спарювання називається структурою популяції і може мати глибокий вплив на розподіл генетичних варіацій всередині та серед природних популяцій.
Популяції часто можуть відрізнятися за частотами алелів, або через генетичний дрейф, або відбір, що спричиняє диференціацію між популяціями. У цьому розділі ми поговоримо про деякі способи узагальнення та візуалізації генетичної структури популяції. Диференціація населення також є основним драйвером кореляцій в алельному стані між локусами, і ми розпочнемо обговорення цих кореляцій в кінці цього розділу. Однією з причин говорити про структуру населення так рано в книзі є те, що узагальнення структури популяції часто є ключовим початковим етапом в популяційному геномному аналізі. Таким чином, ви часто стикаєтеся з резюме та візуалізації структури населення, коли ми читаємо дослідницькі статті, тому добре мати певне розуміння того, що вони представляють.
Інбридинг як зведення структури популяції
Наші твердження про інбридинг та коефіцієнти інбридингу являють собою один природний спосіб узагальнити структуру популяції. У попередньому розділі ми визначили інбридинг як наявність батьків, які більш тісно пов'язані один з одним, ніж дві особини, набрані випадковим чином з якоїсь еталонної популяції. Закономірно виникає питання: Яку довідкову популяцію ми повинні використовувати? Хоча я не можу виглядати інбредним порівняно з частотами алелів у Сполученому Королівстві (Великобританія), звідки я родом, мої батьки, безумовно, не є двома особами, залученими випадковим чином із світового населення. Якби ми оцінили мій коефіцієнт інбридингу,\(F\) використовуючи частоти алелів у Великобританії, він був би близьким до нуля, але, ймовірно, був би більшим, якби ми використовували світові частоти. Це пов'язано з тим, що існує дещо нижчий рівень очікуваної гетерозиготності у Великобританії, ніж у людському населенні у всьому світі в цілому.
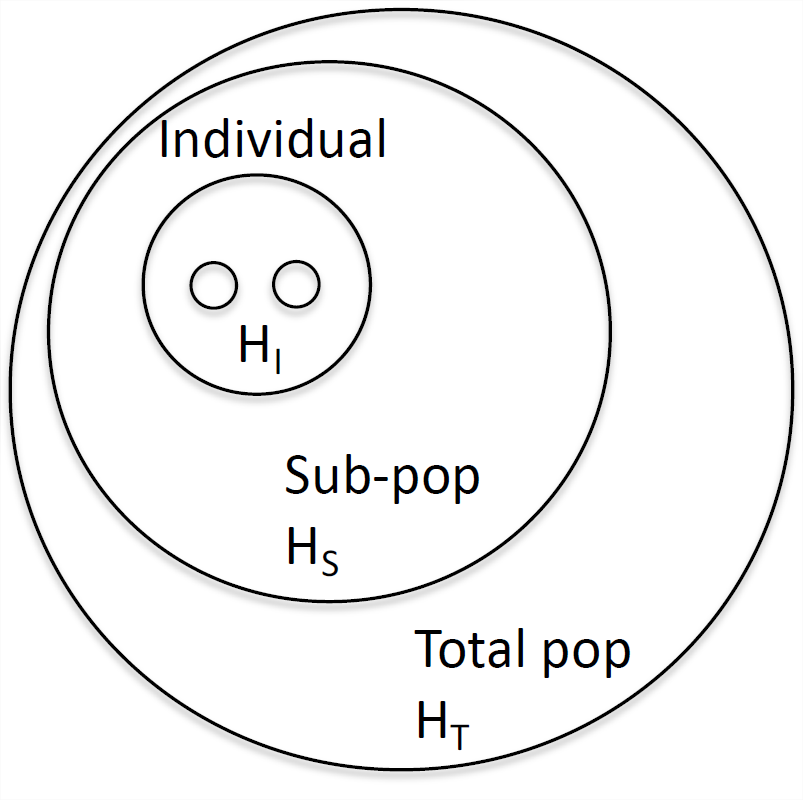
Спираючись на цю ідею коефіцієнтів інбридингу, оцінених на різних рівнях, розроблено набір «F-статистики» (також званих «індексами фіксації»), які формалізують ідею інбридингу стосовно різних рівнів структури популяції. Див. Малюнок\(\PageIndex{1}\) для принципової схеми. Райт визначається\(F_{\mathrm{XY}}\) як кореляція між випадковими гаметами, проведеними з одного рівня\(X\), щодо рівня\(Y\). Ми повернемося до того, чому\(F\) -статистика - це твердження про кореляції між алелями всього за мить. Один з поширених\(F\)\(F_{\mathrm{IS}}\) -statistic є, який є коефіцієнтом інбридингу між\(I\) індивідом () і субпопуляцією (\(S\)). Розглянемо єдиний локус, де в субпопуляції (\(S\))\(H_I=f_{12}\) частка особин гетерозиготна. У цій субпопуляції нехай частота алелів\(A_1\) буде такою\(p_S\), що очікувана гетерозиготність при випадковому спарюванні є\(H_S = 2 p_S (1 - p_S)\). Напишемо\(F_{\mathrm{IS}}\) як
\[F_{\mathrm{IS}} = 1-\frac{H_I}{H_S}= 1-\frac{f_{12}}{2p_Sq_S}, \label{eqn:FIS}\]
прямий аналог\ ref {EQN:THAT}. Звідси\(F_{\mathrm{IS}}\) і відносна різниця між спостережуваною і очікуваною гетерозиготністю внаслідок відхилення від випадкового спаровування всередині субпопуляції. Ми також могли б порівняти спостережувану гетерозиготність у індивідів (\(H_I\)) з очікуваною в загальній популяції,\(H_T\). Якщо частота аллеля\(A_1\) в загальній популяції є\(p_T\), то можна писати\(F_{\mathrm{IT}}\) як
\[F_{\mathrm{IT}} =1-\frac{H_I}{H_T}= 1-\frac{f_{12}}{2p_Tq_T}, \label{eqn:FIT}\]
який порівнює гетерозиготність у осіб з очікуваною в загальній популяції. Як просте продовження цього, ми могли б уявити порівняння очікуваної гетерозиготності в субпопуляції (\(H_S\)) з очікуваною в загальній популяції\(H_T\), за допомогою\(F_{\mathrm{ST}}\):
\[F_{\mathrm{ST}} = 1-\frac{H_S}{H_T}=1-\frac{2p_Sq_S}{2p_Tq_T} \label{eqn:FST}.\]
Ми можемо пов'язати три\(F\) -статистичні дані один з одним як
\[(1-F_{\mathrm{IT}}) =\frac{H_I}{H_S} \frac{H_S}{H_T}=(1-F_{\mathrm{IS}})(1-F_{\mathrm{ST}}). \label{eqn:F_relationships}\]
Отже, зменшення гетерозиготності у осіб порівняно з очікуваним у загальній популяції може бути розкладено на зменшення гетерозиготності індивідів порівняно з субпопуляцією та зменшення гетерозиготності від загальної популяції до субпопуляції.
Якщо ми хочемо отримати резюме структури населення по декількох субпопуляціях, ми можемо усереднити\(H_I\) та/або\(H_S\) популяції, і використовувати\(p_T\) обчислену шляхом усереднення\(p_S\) по субпопуляціях (або наші зразки з субпопуляцій). Наприклад, середній показник\(\bar{F_{\mathrm{ST}}}\) по\(K\) субпопуляціях (вибірка з однаковими зусиллями) становить
\[\bar{F_{\mathrm{ST}}} = 1 - \frac{\bar{H}_{S}}{H_T},\]
де\(\bar{H}_S = \frac{1}{K} \sum_{i = 1}^{K} H_{S}^{(i)}\), і\(H_{S}^{(i)} = 2 p_{i} q_{i}\) є очікувана гетерозиготність в субпопуляції\(i\). Звідси випливає, що середня гетерозиготність субпопуляцій\(\bar{H}_S \leq H_T\)\(\bar{F_{\mathrm{ST}}} \geq 0\) і т\(\bar{F_{\mathrm{IS}}} \leq \bar{F_{\mathrm{IT}}}\). Це спостереження про те, що середня гетерозиготність субпопуляцій повинна бути меншою, ніж у загальної популяції, називається ефектом Уоллунда. Крім того, якщо у нас є кілька сайтів, ми можемо замінити\(H_I\)\(H_S\), і\(H_T\) з їх середніми по локусах (як зазначено вище).
У виду лемурів ви оцінюєте частоту алелів\(20\%\). У певній популяції ви оцінюєте, що частота алелів є\(10\%\). У цій популяції\(9\%\) гетерозигота є тільки з особин. Що таке\(F_{IT}\)\(F_{ST}\), і\(F_{IS}\) для цієї популяції?
Як приклад порівняння загальногеномної оцінки з оцінкою окремих локусів\(F_{ST}\) ми можемо розглянути деякі дані синьо-і золотистокрилих очеретяків (Vermivora cyanoptera та V. chrysoptera 1-2 & 5-6 на рис.\ ref {рис:blue_golden_ очерки}).

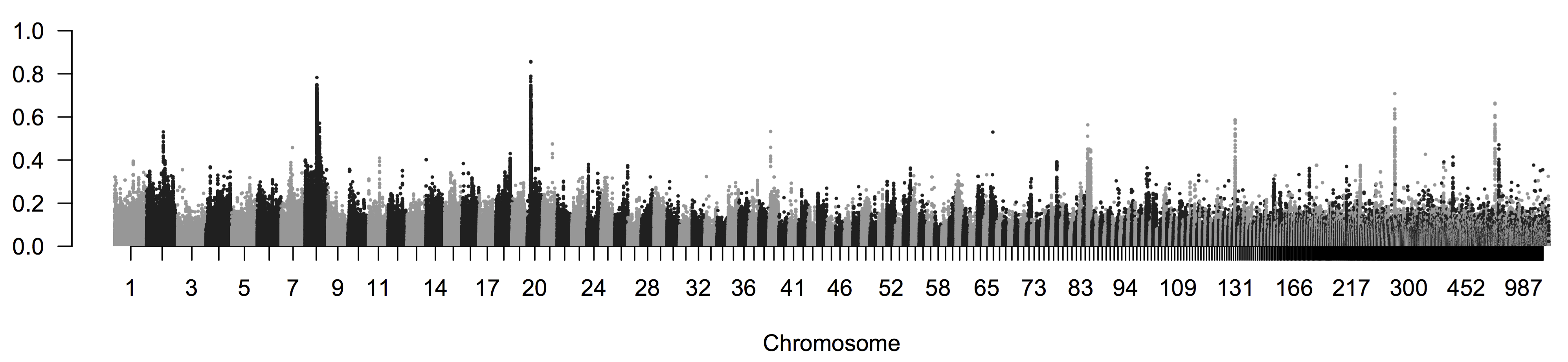
Ці два види поширені по східній Північній Америці, при цьому золотистокрила очеретянка має менший, більш північний ареал. Вони досить різні з точки зору оперення, але вже давно відомо, що мають схожі пісні та екології. Два види легко гібридизуються в дикій природі; насправді два інших раніше визнаних виду, очеретянка Брюстера та Лоуренса (4 & 3 in\ ref {fig:blue_golden_warblers}), насправді виявляються просто гібридами між цими двома видами. Золотокрила очеретянка занесена до списку «загрозливих» під дією канадських зникаючих видів, оскільки її середовище проживання знаходиться під тиском людської діяльності та завдяки зростаючій гібридизації з синьо-крилою очеретявою, яка рухається на північ у свій ареал. досліджували геноміку популяції цих очеретяків, послідовність десяти золотих і десяти синьо-крилих очеретянок. Вони виявили дуже низьку розбіжність серед цих видів, із загальним геномом\(F_{ST}=0.0045\). На рисунку\ ref {Fig:Warbler_FST}, за SNP\(F_{ST}\) усереднений у вікні\(2000\) bp, що рухаються вздовж генома. Середній показник дуже низький, але деякі регіони дуже високі\(F_{ST}\) виділяються. Майже всі ці регіони відповідають великим різницям частот алелів на локусах в або близьких до генів, які, як відомо, беруть участь у відмінностях забарвлення оперення у інших птахів.
Щоб проілюструвати ці частотні відмінності Toews et al. (2016) генотипізували SNP в кожному з цих високих\(F_{ST}\) регіонів. Ось їх генотипування підраховує від SNP, що розділяє на аллель 1 і 2, в регіоні Wnt, ключовий регуляторний ген, який бере участь у розвитку пера:
| види | 11 | 12 | 22 |
| Синьокрилі | 2 | 21 | 31 |
| Золотокрилий | 48 | 12 | 1 |
З посиланням на таблицю Wnt -аллелів підрахунку:
- Обчислити\(F_{IS}\) в синьо-крилих очеретявок.
- Обчисліть\(F_{ST}\) для субпопуляції синьо-крилих очеретявок порівняно з комбінованим зразком.
- Обчисліть\(F_{ST}\) середнє значення для обох субпопуляцій.
Інтерпретації F-статистики
Давайте тепер повернемося до визначення Райтом\(F\) -статистики як кореляцій між випадковими гаметами, намальованими з того ж рівня\(X\), відносно рівня\(Y\). Без втрати спільності ми можемо думати\(X\) як про індивідів і\(S\) як про субпопуляцію. \(F_{\mathrm{IS}}\)Переписуючи в терміні спостережуваних частот гомозигот (\(f_{11}\),\(f_{22}\)) і очікуваних гомозиготності (\(p_{S}^2\),\(q_{S}^2\)) знаходимо
\[F_{\mathrm{IS}} = \frac{2p_Sq_S - f_{12}}{2p_Sq_S} = \frac{f_{11}+f_{22} - p_S^2 - q_S^2}{2p_Sq_S}, \label{eqn:Fascorr}\]
використовуючи те\(p^2+2pq+q^2=1\), що, і\(f_{12} = 1 - f_{11} - f_{12}\). Форма рівняння (\ ref {eQn:Fascorr}) показує, що\(F_{\mathrm{IS}}\) це коваріація між парами алелів, знайдених у індивіда, поділена на очікувану дисперсію при біноміальній вибірці. Таким чином,\(F\) -статистику можна розуміти як кореляцію між алелями, взятими з популяції (або індивіда) вище очікуваного випадково (тобто малювання алелів, вибраних випадковим чином з деякої більш широкої популяції).
Ми також можемо інтерпретувати\(F\) -статистику як пропорції дисперсії, що пояснюються різними рівнями структури населення. Щоб переконатися в цьому, давайте подумаємо про\(F_{\mathrm{ST}}\) усереднені над\(K\) субпопуляціями, чиї частоти є\(p_1,\dots,p_K\). Частота в загальній чисельності населення становить\(p_T=\bar{p} = \frac{1}{K} \sum_{i=1}^K p_i\). Тоді ми можемо написати
\[\begin{aligned} F_{\mathrm{ST}} &= \frac{2 \bar{p}\bar{q} - \frac{1}{K}\sum_{i=1}^K 2p_iq_i }{2 \bar{p}\bar{q}} = \frac{ \left(\frac{1}{K} \sum_{i=1}^K p_i^2 + \frac{1}{K} \sum_{i=1}^K q_i^2 \right) - \bar{p}^2-\bar{q}^2 }{2 \bar{p}\bar{q}} \nonumber\\ &= \frac{\mathrm{Var}(p_1,\dots,p_K)}{\mathrm{Var}(\bar{p})}, \label{eqn:F_as_propvar}\end{aligned}\]
що показує,\(F_{\mathrm{ST}}\) що частка дисперсії пояснюється мітками субпопуляції.
Інші підходи до структури населення
Існує широкий спектр методів опису закономірностей структури популяції в генетичних наборах даних популяції. Ми коротко обговоримо два широкі класи методів, які часто зустрічаються в літературі: методи присвоєння та аналіз основних компонентів.
Методи присвоєння
Тут ми опишемо просте імовірнісне завдання, щоб знайти ймовірність того, що індивід невідомої популяції походить з однієї із\(K\) заздалегідь визначених популяцій. Наприклад, в Африці існує три широкі популяції шимпанзе (Pan troglodytes): західна, центральна та східна. Уявіть, що у нас є шимпанзе, походження якого невідоме (наприклад, це з незаконної приватної колекції). Якщо ми генотипізували набір незв'язаних маркерів з групи особин, представницьких цих популяцій, ми можемо обчислити ймовірність того, що наш шимпанзе походить від кожної з цих популяцій.
Потім ми коротко пояснимо, як розширити цю ідею, щоб скупчити набір осіб у\(K\) спочатку невідомі популяції. Цей метод є спрощеною версією того, що роблять алгоритми кластеризації генетики популяцій, такі як СТРУКТУРА та ДОМІШКА.
Простий метод присвоєння
Ми маємо дані генотипу з незв'язаних\(S\) біаллельних локусів для\(K\) популяцій. Частота алелів алеля\(A_1\) в\(l\) локусі в популяції\(k\) позначається\(p_{k,l}\) тим, що частоти алелів у населення 1 є\(p_{1,1},\cdots p_{1,L}\) і популяція 2 є\(p_{2,1},\cdots p_{2,L}\) і так далі.
Ви генотипуєте нову особину з невідомої популяції в цих\(L\) локусах. Генотип цієї особини в\(l\) локусі є\(g_l\), де\(g_l\) позначає кількість копій алеля, яку\(A_1\) ця особина несе в цьому локусі (\(g_l=0,1,2\)).
Імовірність генотипу цієї особини в локусі, обумовленого\(l\) похідним від популяції\(k\), тобто їх алелі, які є випадковим витягом HW з популяції\(k\), становить
\[\mathbb{P}(g_l | \textrm{pop k}) = \begin{cases} (1-p_{k,l})^2 & g_l=0 \\ 2 p_{k,l} (1-p_{k,l}) & g_l=1\\ p_{k,l}^2 & g_l=2 \end{cases}\]
Припускаючи, що локуси незалежні, ймовірність генотипу індивіда по всіх локусах S, умовна від індивіда, що надходить з популяції\(k\), становить
\[\mathbb{P}(\textrm{ind.} | \textrm{pop k}) = \prod_{l=1}^S \mathbb{P}(g_l | \textrm{pop k}) \label{eqn_assignment}\]
Ми хочемо знати ймовірність того, що ця нова людина походить від населення\(k\), тобто\(P(\textrm{pop k} | \textrm{ind.})\). Ми можемо отримати це через правило Байєса
\[\mathbb{P}(\textrm{pop k} | \textrm{ind.}) = \frac{\mathbb{P}(\textrm{ind.} | \textrm{pop k}) \mathbb{P}(\textrm{pop k})}{\mathbb{P}(\textrm{ind.})}\]
де
\[\mathbb{P}(\textrm{ind.}) = \sum_{k=1}^K \mathbb{P}(\textrm{ind.} | \textrm{pop k}) \mathbb{P}(\textrm{pop k})\]
нормалізує константа. Ми можемо інтерпретувати\(\mathbb{P}(\textrm{pop k})\) як попередню ймовірність того, що індивід походить від населення\(k\), і якщо ми не матимемо інших попередніх знань, ми будемо вважати, що нова людина має однакову ймовірність надходження від кожної популяції\(\mathbb{P}(\textrm{pop k})=\frac{1}{K}\).
інтерпретуємо
\[\mathbb{P}(\textrm{pop k} | \textrm{ind.})\]
як задня ймовірність того, що наш новий індивід походить від кожного з наших\(1,\cdots, K\) популяцій.
Більш складні версії цього тепер використовуються, щоб дозволити гібридам, наприклад, ми можемо мати\(q_k\) частку генома нашої людини походить від популяції\(k\) та оцінити набір\(q_k\).
Повертаючись до нашого прикладу шимпанзе, уявіть, що ми генотипізували набір особин із західних та східних популяцій у двох SNP (ми ігноруємо центральну популяцію, щоб спростити ситуацію). Частота капітального аллеля при двох СНП (\(A/a\)і\(B/b\)) задається
| Населення | локус А | локус B |
|---|---|---|
| Західний | \(0.1\) | \(0.85\) |
| Східний | \(0.95\) | \(0.2\) |
- Наша особина, походження якої невідоме, має генотип\(AA\) в першому локусі і\(bb\) на другому. Яка задня ймовірність того, що наша людина походить від західного населення проти популяції східних шимпанзе?
- (Хитріше) Давайте припустимо, що наша особина з частини А є гібридом (не обов'язково F1). У кожному локусі, з імовірністю,\(q_W\) наша особина витягує алель із західної популяції і з\(q_E=1-q_W\) ймовірністю черпає алель зі східної популяції. Яка ймовірність наданого генотипу нашої особистості\(q_W\)?
Необов'язково Ви можете побудувати цю ймовірність як функцію\(q_W\). Як змінюється ваш сюжет, якщо наша особина гетерозиготна в обох локусах?
Кластеризація на основі методів присвоєння
Хоча це здорово, щоб мати можливість призначити наших особин певній популяції, ці ідеї можна підштовхнути, щоб дізнатися про те, як найкраще описати наші дані генотипу з точки зору дискретних популяцій, не призначаючи жодної з наших особин до популяцій апріорі. Ми хочемо скупчити наших особин в\(K\) невідомі групи населення. Ми починаємо з присвоєння нашим особам випадковим чином цим\(K\) популяціям.
- Враховуючи ці завдання, ми оцінюємо частоти алелів у всіх наших локусах у кожній популяції.
- Враховуючи ці частоти алелів, ми вирішили перепризначити кожну людину до популяції\(k\) з ймовірністю, заданою\ ref {eqn_assignion}.
Ми повторюємо кроки 1 та 2 для багатьох ітерацій (технічно цей підхід відомий як Вибірка Гіббса). Якщо дані досить інформативні, завдання та частоти алелів швидко сходяться на наборі ймовірних призначень популяцій та частот алелів для цих популяцій.

[рис.: шимпан_структура]
Для цього в повній байєсівській схемі нам потрібно розмістити пріори на частотах алелів (наприклад, можна використовувати бета-розподіл попереднього). Технічно ми використовуємо суглоб задньої частини наших частот алелів і завдань. Такі програми, як СТРУКТУРА, використовують цей тип алгоритму для кластерування індивідів «без нагляду» (тобто вони розробляють, як призначити людей до невідомого набору популяцій). Див. Рисунок\ ref {fig:chimp_structure} для прикладу використання СТРУКТУРИ для визначення структури популяції шимпанзе.
Структурно-подібні методи виявилися неймовірно популярними та корисними при дослідженні структури популяції всередині видів. Однак результати цих методів відкриті для неправильного тлумачення; див. Недавнє обговорення. Дві поширені помилки - 1) прийняття результатів структурно-подібних підходів для певної конкретної цінності K і прийняття цього, щоб представляти найкращий спосіб опису популяційно-генетичних варіацій. 2) Думаючи, що ці кластери представляють «чисті» родові популяції.
Немає правильного вибору K, кількості кластерів, на які потрібно розділити. Існують методи оцінки «найкращого» K за деякими статистичними показниками, враховуючи певний набір даних, але це не те саме, що сказати, що це найбільш значущий рівень, на якому можна узагальнити структуру населення в даних. Наприклад, запуск СТРУКТУРИ на всесвітній людській популяції при низькому значенні K призведе до скупчення населення, які приблизно узгоджуються з континентальним населенням. Однак це не говорить нам про те, що присвоєння походження на рівні континентів є особливо значущим способом розбиття індивідів. Запуск тих самих даних для більш високого значення K або в межах континентальних регіонів призведе до набагато більш тонкого поділу континентальних груп. Жоден із цих шарів структури населення не є привілейованим як більш значущий, ніж інший.
Заманливо думати про ці скупчення як про родові популяції, які самі по собі не є наслідком домішки. Однак це не так, наприклад, запуск STRUCTURE на всесвітніх людських даних ідентифікує кластер, який містить багато європейських індивідів, однак, на основі стародавньої ДНК ми знаємо, що сучасні європейці є сумішшю різних родових груп.
Аналіз основних компонентів
Аналіз основних компонентів (PCA) є загальним статистичним підходом для візуалізації високошвидкісних даних і використовується багатьма полями. Ідея PCA полягає в тому, щоб дати розташування кожній окремій точці даних на кожній з невеликих осей основних компонентів. Ці осі ПК обрані для відображення основних осей зміни в даних, причому перший ПК є тим, що пояснює найбільшу дисперсію, другий самий другий, і так далі. Використання PCA в популяційній генетиці було піонером Каваллі-Сфорца та його колег, і тепер з великими наборами даних генотипування PCA повернувся.
Розглянемо набір даних, що складається з N осіб на\(S\) біаллельних SNP. Дані генотипу\(i^{th}\) індивіда в\(\ell\) локусі приймають значення\(g_{i,\ell}=0,1,\; \text{or} \; 2\) (що відповідає кількості копій\(A_1\) алелю, яку людина несе на цьому SNP). Ми можемо думати про це як\(N \times S\) матрицю (де зазвичай\(N \ll S\)).
Позначаючи середню частоту алелів зразка при SNP\(\ell\)\(p_{\ell}\), прийнято стандартизувати генотип наступним чином
\[\frac{g_{i,\ell} - 2 p_{\ell}}{\sqrt{2 p_{\ell}(1-p_{\ell})}} \label{eqn:std_allele_freq}\]
тобто на кожному SNP ми центруємо генотипи, віднімаючи середній генотип (\(2p_{\ell}\)) і ділимо через квадратний корінь очікуваної дисперсії, припускаючи, що алелі відбираються біноміально від середньої частоти (\(\sqrt{2 p_{\ell} (1-p_{\ell})}\)). Роблячи це з усіма нашими генотипами, ми формуємо матрицю даних (розмірності\(N \times S\)). Потім ми можемо виконати аналіз основних компонентів цієї матриці даних, щоб виявити основні осі дисперсії генотипу в нашому зразку. Рисунок\ ref {Fig:Chimp_PCA} показує PCA з використанням тих самих даних шимпанзе, що і на малюнку\ ref {fig:chimp_structure}.
![Аналіз основних компонентів з використанням тих же даних шимпанзе, що і на малюнку [рис:chimp_structure]. Тут розміщено розташування кожної людини на перших двох основних компонентах (так званих власних векторів) на лівій панелі та на другій та третій основних компонентах (власні вектори) у правій панелі (). У PCA особи ідентифікуються як всі з одного походження за структурою скупчення разом за популяцією (тверді кола). У той час як дев'ять особин, ідентифікованих СТРУКТУРОЮ як гібриди (відкриті кола) здебільшого потрапляють в проміжні місця в PCA. Є дві особини (червоні відкриті кола) повідомляється як про певну популяцію, але це, але, здається, гібриди.](/figures/Becquet_et_al_STRUCTURE_journal_pgen_0030066_g002.png)
[Рис: шимпан_ПКА]
Варто скористатися моментом, щоб глибше заглибитися в те, що ми тут робимо. Існує ряд еквівалентних способів мислення про те, що робить PCA. Одним із таких способів є думка, що коли ми робимо PCA, ми будуємо індивіда за індивідуальною матрицею коваріації та виконуємо розкладання власних значень цієї матриці (з власними векторами є ПК). Ця індивіда за індивідуальною коваріаційною матрицею має записи,\([i,~j]\) задані
\[\frac{1 }{S-1} \sum_{\ell=1}^S \frac{(g_{i,\ell} - 2p_{\ell})(g_{j,\ell} - 2p_{\ell})}{2 p_{\ell}(1-p_{\ell})} \label{eqn:kinship_mat}\]
Зауважте, що це вибіркова коваріація наших стандартизованих частот алелів (\ ref {eqn:std_allele_freq}), і дуже схожа на ті, з якими ми стикалися при обговоренні\(F\) -statistics як кореляції (\ ref {eqn:fascorr}), за винятком того, що зараз ми запитуємо про коваріацію між двома людьми вище які очікували, якщо вони обидва були взяті із загальної вибірки випадковим чином (а не коваріація алелів всередині однієї людини). Отже, виконуючи PCA на даних, ми дізнаємося про основні (ортогональні) осі матриці спорідненості.
Як приклад застосування ПСА розглянемо випадок передбачуваного кільцевого виду в комплексі видів зеленуватого очеретянки (Phylloscopus trochiloides). Цей набір підвидів існує в кільці навколо краю Гімалайського плато. Зібрані\(95\) зеленуваті зразки очеретянки з\(22\) ділянок навколо кільця, а місця відбору проб показані на малюнку\ ref {Fig:Gwarbler_geo}.

[Рис: Гварблер_GEO]
Вважається, що ці очеретянки поширюються з півдня, на північ у двох різних напрямках навколо негостинного Гімалайського плато, встановлюючи популяції вздовж західного краю (зелені та сині популяції) та східного краю (жовті та червоні популяції). Коли вони вступили в вторинний контакт в Сибіру, вони були репродуктивно ізольовані один від одного, розвиваючи різні пісні і накопичуючи інші репродуктивні бар'єри один від одного, коли вони поширювалися незалежно на північ навколо плато, такі, що P. t. viridanus (синій) і Популяції P. t. plumbeitarsus (червоні) в даний час утворюють стабільну гібридну зону.

[рис.: зеленуватою_очеретянка]
отримані дані послідовності для своїх зразків при 2334 SNPs. На малюнку\ ref {fig:warbler_heat} ви можете побачити матрицю коефіцієнтів спорідненості, використовуючи\ ref {eqn:kinship_mat}, між усіма парами зразків. Ви вже можете побачити багато про структуру населення в цій матриці. Зверніть увагу, як червоні та жовті зразки, які, як вважають, отримані від східного маршруту навколо Гімалаїв, мають більш високу спорідненість один з одним, а синій і (більшість) зелених зразків із західного маршруту утворюють аналогічно близьку групу з точки зору їх вищої спорідненості.
![Матриця коефіцієнтів спорідненості розрахована для 95 зразків зеленуватих очеретяків. Кожна клітинка матриці дає попарний коефіцієнт спорідненості, розрахований для конкретної пари. Більш гарячі кольори, що вказують на більш високу спорідненість. Мітки x і y індивідів є популяції міток з Рисунок [рис:Gwarbler_Geo], і пофарбовані міткою підвиду, як на цьому малюнку. Рядки та стовпці були організовані для скупчення людей з високими спорідненнями.](/figures/warbler_PCA_figs/warbler_heatmap.png)
[рис:варблер_тепло]
Потім ми можемо виконати PCA на цій матриці спорідненості, щоб визначити основні осі варіації в наборі даних. На малюнку\ ref {Fig:Warbler_PCA} показані зразки, нанесені на перших двох ПК.
![95 зелених зразків очеретянки нанесені на свої місця розташування на перших двох основних компонентах. Мітки індивідів - це популяції міток з малюнка [рис:Gwarbler_geo], і пофарбовані міткою підвиду, як на цьому малюнку.](/figures/warbler_PCA_figs/warbler_PCAmap.jpg)
[Рис: Warbler_PCA]
Два основних шляхи розширення явно займають різні частини простору ПК. Перший основний компонент розрізняє населення, що проходять з півночі на південь уздовж західного шляху розширення, тоді як другий основний компонент розрізняє населення, що проходять з півночі на південь уздовж східного шляху розширення. Таким чином, генетичні дані підтверджують гіпотезу про те, що зеленуваті очеретянки видобувалися під час переміщення навколо Гімалайського плато. Однак, як зазначається, це також передбачає додаткові ускладнення традиційного погляду цих очеретявок як нерозривного кільцевого виду, випадку видоутворення шляхом безперервної географічної ізоляції. Підвид Ludlowi демонструє значний генетичний розрив, причому найбільш південні зразки MN кластеруються з підвидами Trochiloides як у матриці PCA, так і в матриці спорідненості (рис.\ ref {Fig:Warbler_pca} і\ ref {fig:warbler_eat}), незважаючи на те, що він набагато більше географічно близькі до інших зразків Ладлові. Це говорить про те, що генетична ізоляція є не просто результатом географічної відстані, а інші біогеографічні бар'єри повинні розглядатися у випадку цього зламаного кільцевого виду.
Нарешті, хоча PCA є чудовим інструментом для візуалізації генетичних даних, при його інтерпретації потрібно дотримуватися обережності. U-подібна форма у випадку ПК із зеленуватою очеретявою може відповідати деякому низькому рівню потоку генів між червоною та синьою популяціями, витягуючи їх генетично ближче один до одного та допомагаючи сформувати генетичне кільце, а також географічне кільце. Однак U-подібні форми, як очікується, з'являться в PCA, навіть якщо наші популяції просто розташовані уздовж лінії, і більш складні геометричні розташування популяцій у просторі ПК можуть призвести до простих географічних моделей. Висновок географічної та популяційно-генетичної історії видів вимагає застосування цілого ряду інструментів; див. І для більш детального обговорення зеленуватих очеретяків.
Кореляції між локусами, порушення рівноваги зв'язків та рекомбінація
До теперішнього часу ми цікавилися кореляціями між алелями в одному місці, наприклад, кореляції всередині осіб (інбридинг) або між особами (спорідненість). Ми бачили, як взаємозв'язок між батьками впливає на те, наскільки їх потомство інбредне. Тепер перейдемо до кореляцій між алелями в різних локусах.
Рекомбінація
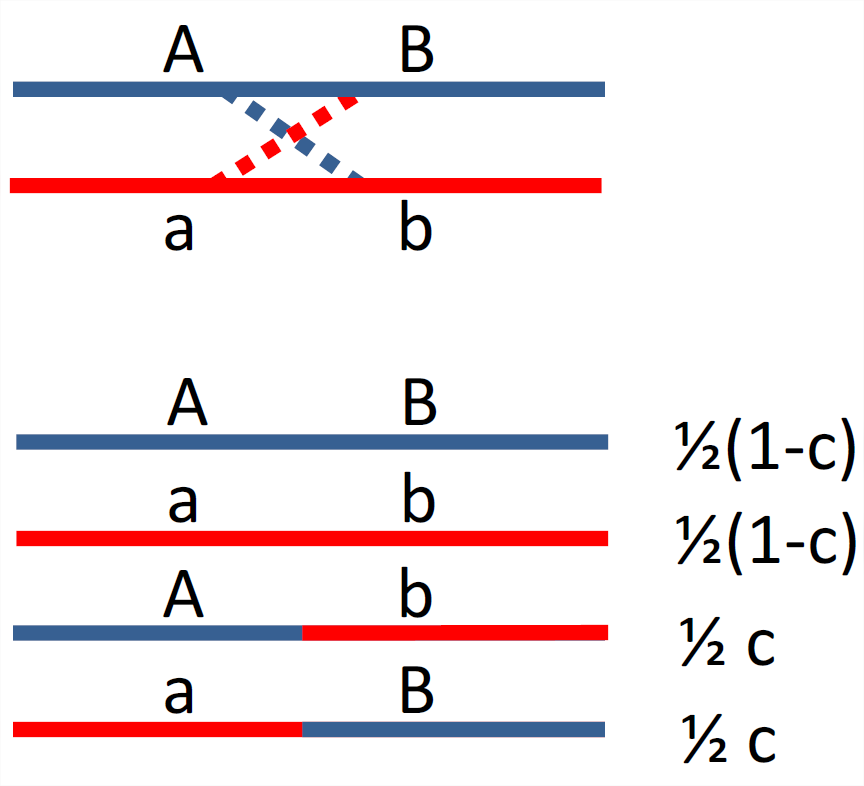
Щоб зрозуміти кореляції між локусами, нам потрібно зрозуміти рекомбінацію трохи ретельніше. Розглянемо гетерозиготну особина, що містить\(AB\) і\(ab\) гаплотипи. Якщо між нашими двома локусами у цієї особини не відбувається жодної рекомбінації, то ці два гаплотипи будуть передаватися неушкодженими наступному поколінню. Хоча якщо між двома батьківськими гаплотипами відбувається рекомбінація (тобто непарна кількість перетинання подій), то\(\frac{1}{2}\) час, коли дитина отримує\(Ab\) гаплотип і\(\frac{1}{2}\) час, коли дитина отримує\(aB\) гаплотип. Див. Рисунок\ ref {fig:recom_cartoon}. Ефективно рекомбінація розриває асоціацію між локусами. Для зв'язаних маркерів ми визначимо фракцію рекомбінації (\(x\)) як ймовірність непарної кількості перетину подій між нашими локусами в одному мейозі. Рекомбінаційна фракція між парою локусів може варіюватися від\(0\) до\(\frac{1}{2}\), з\(c=\frac{1}{2}\) відповідними маркерами досить далеко один від одного на хромосомі, що багато подій рекомбінації відбуваються між ними (локуси на різних аутомосомах також мають \(c=\frac{1}{2}\)). На практиці нас часто цікавлять відносно короткі регіони, такі, що рекомбінація є відносно рідкісною, і тому ми можемо подумати\(c=c_{BP}L \ll \frac{1}{2}\), що, де\(c_{BP}\) середня швидкість рекомбінації (в Морганах) на базову пару (зазвичай\(\sim 10^{-8}\)) і L є кількість пар основ, що розділяють наші два локуси.
Порушення рівноваги зчеплення
(жахлива) фраза зв'язок disequilribrium (LD) відноситься до статистичної незалежності (тобто кореляції) алелів у популяції в різних локусах. Це фантастично корисна концепція; ЛД є ключем до нашого розуміння різноманітних тем, від сексуального відбору та видоутворення до меж досліджень асоціації в масштабах генома.
Наші два біаллельні локуси, які розділяють алелі\(A/a\) і\(B/b\), мають частоти алелів\(p_A\) і\(p_B\) відповідно. Частота двох гаплотипів локусів AB є\(p_{AB}\), і так само для наших інших трьох комбінацій. Якщо наші локуси були статистично незалежними\(p_{AB} = p_Ap_B\), то, інакше\(p_{AB} \neq p_Ap_B\) ми можемо визначити коваріацію між\(A\) алелями\(B\) та алелями в наших двох локусах як
\[D_{AB} = p_{AB} - p_Ap_B \label{eqn:LD_def}\]
і так само для інших наших комбінацій на наших двох локусах (\(D_{Ab},~D_{aB},~D_{ab}\)). Гамети з двома подібними випадковими алелями (наприклад, A і B, або a і b) відомі як гамети зв'язку, а ті, що мають різні алелі випадку, відомі як відштовхувальні гамети (наприклад, a і B, або A і b). Тоді ми можемо думати про вимірювання надлишку зчеплення з відштовхувальними гаметами.\(D\) Ці\(D\) статистичні дані всі тісно пов'язані один з одним як\(D_{AB} = - D_{Ab}\) і так далі. Таким чином, нам потрібно лише вказати один,\(D_{AB}\) щоб знати їх усіх, так що ми скинемо індекс і просто посилатися на\(D\). Також зручним результатом є те, що ми можемо переписати нашу частоту гаплотипу\(p_{AB}\) як
\[p_{AB} = p_Ap_B+D. \label{eqn:ABviaD}\]
Якщо\(D=0\) ми скажемо, що два локуси знаходяться в рівновазі зв'язку, тоді як якщо\(D>0\) або\(D<0\) ми скажемо, що локуси знаходяться в порушенні рівноваги зв'язку (ми, можливо, захочемо перевірити, чи\(D\) статистично відрізняється від\(0\) перш ніж зробити цей вибір). Порушення рівноваги зв'язків - жахлива фраза, оскільки вона ризикує заплутати поняття генетичного зв'язку та порушення рівноваги зв'язків. Генетичним зв'язком називають зв'язок множинних локусів через те, що вони передаються через мейоз разом (найчастіше тому, що локуси знаходяться на одній хромосомі). Порушення рівноваги зв'язків просто відноситься до коваріації між алелями в різних локусах; частково це може бути пов'язано з генетичним зв'язком цих локусів, але не обов'язково означає це (наприклад, генетично незв'язані локуси можуть бути в ЛД через структуру популяції).
Ви генотип 2 біалельних локусів (A & B), що розділяються на два підвиди миші (1 і 2), які випадково спаровуються між собою, але історично не схрещуються, оскільки вони видозмінювалися. Частоти гаплотипів у кожній популяції становлять:
| Поп | \(p_{AB}\) | \(p_{Ab}\) | \(p_{aB}\) | \(p_{ab}\) |
|---|---|---|---|---|
| 1 | \ (p_ {AB}\)» style="вирівнювання тексту: центр; "> 0.02 | \ (p_ {Ab}\)» style="вирівнювання тексту: центр; "> 0.18 | \ (p_ {aB}\)» style="вирівнювання тексту: центр; "> 0,08 | \ (p_ {ab}\)» style="вирівнювання тексту: центр; "> 0.72 |
| 2 | \ (p_ {AB}\)» style="вирівнювання тексту: центр; "> 0.72 | \ (p_ {Ab}\)» style="вирівнювання тексту: центр; "> 0.18 | \ (p_ {aB}\)» style="вирівнювання тексту: центр; "> 0,08 | \ (p_ {ab}\)» style="вирівнювання тексту: центр; "> 0.02 |
- Скільки ЛД є всередині видів? (тобто оцінка D)
- Якщо ми змішали особини двох видів разом в рівних пропорціях, ми могли б сформувати нову\(p_{AB}\) популяцію з рівною середній частоті\(p_{AB}\) різних видів 1 і 2. Яке значення D візьме в цій новій популяції до того, як будь-яке спарювання матиме шанс відбутися?
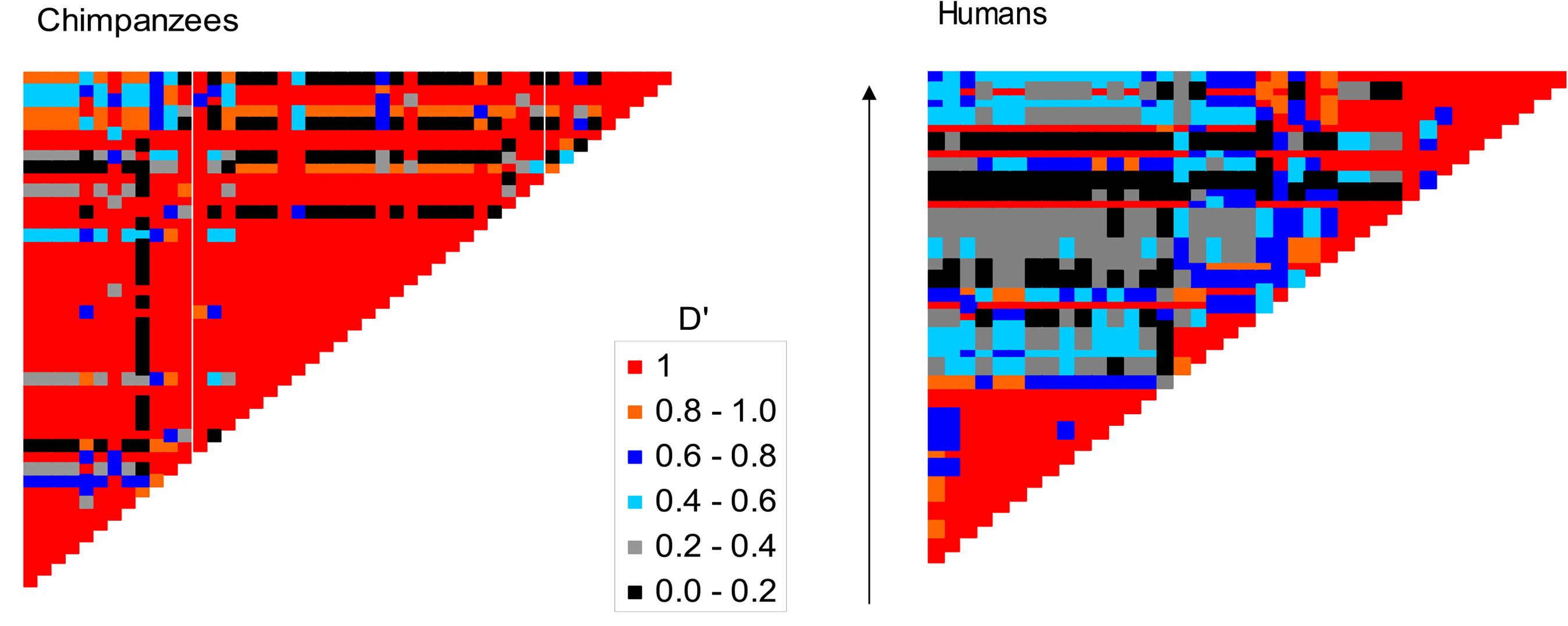
Наша статистика порушення рівноваги зв'язку сильно\(D\) залежить від частот алелів двох задіяних локусів. Одним із поширених способів частково усунути цю залежність і зробити її більш порівнянною по локусах, є поділ\(D\) через її максимально можливу величину з урахуванням частоти локусів. Ця нормована статистика називається\(D^{\prime}\) і варіюється між\(+1\) і\(-1\). На малюнку\ ref {Fig:Taps_Hotspot} є приклад LD в області TAP2 у людини і шимпанзе. Зверніть увагу, як фізично близькі SNP, тобто ті, що близькі до діагоналі, мають більш високі абсолютні значення,\(D^{\prime}\) оскільки тісно пов'язані алелі розділяються рекомбінацією рідше, що дозволяє накопичувати високі рівні ЛД. На великих фізичних відстанях, далеко від діагоналі, знаходиться нижче\(D^{\prime}\). Це особливо помітно для людей, оскільки в цьому регіоні існує інтенсивна, специфічна для людини гаряча точка рекомбінації, яка руйнує ЛД між протилежними сторонами цього регіону.
Ще одна поширена статистика для підведення LD - це те\(r^2\), що ми пишемо як
\[r^2 = \frac{D^2}{p_A(1-p_A) p_B(1-p_B) }\]
Як і\(D\) коваріація, і\(p_A(1-p_A)\) дисперсія алеля, намальованого випадковим чином з локусу\(A\),\(r^2\) - це коефіцієнт кореляції в квадраті.
фракція.

Рисунок\ ref {Fig:mouse_LD} показано\(r^2\) для пар SNP на різних фізичних відстанях у двох популяційних зразках Mus musculus domesticus. Знову LD є найвищим між фізично близькими маркерами, оскільки LD генерується швидше, ніж він може розпастися за допомогою рекомбінації; більш віддалені маркери мають набагато нижчий LD, оскільки тут рекомбінація виграє. Зверніть увагу, що занепад ЛД відбувається набагато повільніше в перехресному популяції передового покоління, ніж у природному дикому спійманому популяції. Така стійкість ЛД по мегабазах обумовлена обмеженою кількістю поколінь для рекомбінації з моменту створення кросу.

Покоління ЛД.
Різні популяційні генетичні сили можуть генерувати ЛД. Вибір може генерувати ЛД, надаючи перевагу певним комбінаціям алелей. Генетичний дрейф також генерує ЛД, не тому, що особливі комбінації алелів сприятливі, а просто тому, що випадково конкретні гаплотипи можуть випадково дрейфувати в частоті. Змішування між різними популяціями також може генерувати ЛД, як ми бачили в питанні миші вище.
Розпад ЛД внаслідок рекомбінації
Зараз ми розглянемо, що відбувається з ЛД протягом поколінь, якщо в дуже великій популяції (тобто немає генетичного дрейфу і частоти наших локусів, таким чином, відповідають їхнім очікуванням), ми дозволимо лише рекомбінації відбутися. Для цього розглянемо частоту нашого\(AB\) гаплотипу в наступному поколінні\(p_{AB}^{\prime}\). Ми втрачаємо\(c\) частину наших\(AB\) гаплотипів, щоб рекомбінація розриваючи наші алелі на частини, але отримуємо частку\(cp_A p_B\) на покоління від інших гаплотипів, що рекомбінуються разом, утворюючи\(AB\) гаплотипи. Таким чином, в наступному поколінні
\[p_{AB}^{\prime} = (1-c)p_{AB} + cp_Ap_B \label{new_hap_freq}\]
Останній термін вище, у\ ref {new_hap_freq},\(c(p_{AB}+p_{Ab})(p_{AB}+p_{aB})\) спрощений, тобто ймовірність рекомбінації в різних диплоїдних генотипах, які можуть генерувати\(p_{AB}\) гаплотип.
Потім ми можемо записати зміну частоти\(p_{AB}\) гаплотипу як
\[\Delta p_{AB} = p_{AB}^{\prime} -p_{AB} = -c p_{AB} + cp_Ap_B = - c D\]
[Рис:LD_Time]
[Рис:ЛД_Реком]
Таким чином, рекомбінація призведе до зменшення частоти,\(p_{AB}\) якщо є надлишок\(AB\) гаплотипів всередині популяції (\(D>0\)), і збільшення, якщо є дефіцит\(AB\) гаплотипів всередині популяції ( \(D<0\)). Наш LD в наступному поколінні
\[\begin{aligned} D^{\prime} & = p_{AB}^{\prime} - p'_{A}p'_{B} \nonumber\\ & = (p_{AB} + \Delta p_{AB}) - (p_{A} + \Delta p_{A})(p_{B} + \Delta p_{B}) \nonumber\\ & = p_{AB} + \Delta p_{AB} - p_{A}p_{B} \nonumber\\ & = (1-c) D\end{aligned}\]
де ми можемо скасувати\(\Delta p_{A}\) і\(\Delta p_{B}\) вище, оскільки рекомбінація змінює лише гаплотип, а не алель, частоти. Отже, якщо рівень ЛД у генерації\(0\) є\(D_0\), рівень\(t\) поколінь пізніше (\(D_t\)) дорівнює
\[D_t= (1-c)^t D_0\]
Рекомбінація діє на зменшення ЛД, і це робить це геометрично зі швидкістю, заданою\((1-c)\). Якщо\(c \ll 1\) тоді ми можемо наблизити це експоненцією і сказати, що
\[D_t \approx D_0 e^{-ct} \label{eqn_LD_decay}\]
що випливає з розширення серії Тейлора, див. Додаток\ ref {EQN:Taylor_Geo}.
Ви знаходите гібридну популяцію між двома підвидами миші, описаними в питанні вище, яка, здається, складається з однакових пропорцій (\(50/50\)) походження двох підвидів. Ви оцінюєте LD між двома маркерами\(D=0.0723\). На підставі попередньої роботи ви оцінюєте, що два локуси розділені рекомбінаційною часткою 0,1. Припускаючи, що ця гібридна популяція велика і була сформована єдиною сумішшною подією, чи можете ви оцінити, як давно ця популяція сформувалася?
Особливо яскравий приклад розпаду ЛД, породженого змішуванням популяцій, пропонує ЛД, створений шляхом схрещування між людьми та неандертальцями. Неандертальці та сучасні люди розійшлися один від одного, ймовірно, більше півмільйона років тому, що дозволило час для накопичення різниць частот алелів між неандертальцем та сучасними людськими популяціями. Дві популяції повернулися у вторинний контакт, коли люди переїхали з Африки протягом останніх ста тисяч років або близько того. Одним з найбільш захоплюючих знахідок секвенування неандертальського генома було те, що сучасні люди з євразійським родом переносять кілька відсотків свого геному, отриманого з геному неандертальця, шляхом схрещування під час цього вторинного контакту. На сьогоднішній день терміни цього схрещування, розглянули LD у сучасних людей між парами алелів, виявлених як похідні від неандертальського генома (і майже відсутні в африканських популяціях). На рисунку\ ref {fig:ld_neanderthal} ми показуємо середню LD між цими локусами як функцію генетичної відстані (\(c\)) між ними, від роботи.

Припускаючи швидкість рекомбінації\(r\), ми можемо пристосувати експоненціальне занепад ЛД, передбачене\ ref {eqn_LD_decay}, до точок даних на цьому малюнку; відповідність показана червоною лінією. Роблячи це, ми оцінюємо\(t=1200\) покоління, або близько 35 тисяч років (використовуючи час людського покоління 29 років). Таким чином, ЛД у сучасних євразійців, між алелями, отриманими в результаті схрещування з неандертальцями, являє собою понад тридцять тисяч років рекомбінації, повільно руйнуючи ці старі асоціації.
Резюме
- Особи часто спаровуються невипадково, наприклад, за географічним положенням, це породжує генетичну структуру населення, яку можна розглядати як форму інбридингу. Цей інбридинг на популяційному рівні призводить до зменшення гетерозиготності в субпопуляціях порівняно із загальною популяцією (якщо частоти алелів відрізняються у різних популяціях).
- \(F\)Статистика Райта може бути використана для вимірювання ступеня структури населення, описуючи зменшення гетерозиготності в різних масштабах, наприклад індивіда порівняно з субпопуляцією (\(F_{IS}\)) або субпопуляція порівняно із загальною чисельністю населення ( \(F_{ST}\)). Ми можемо обчислити ці статистичні дані або в масштабах генома, або за окремими локусами.
- Ці\(F\) статистичні дані можна розуміти як вираження кореляції між алелями, взятими з того ж рівня структури популяції, або частки генетичної дисперсії, поясненої структурою населення.
- Інші способи візуалізації структури популяції включають структуроподібні підходи, які засновані на присвоєнні індивідів популяціям на основі ймовірності їх генотипу заданих частот алелів (методів присвоєння) та навчання присвоєнню індивідів до дискретних популяцій. Інший поширений підхід спирається на виявлення основних осей варіацій у спорідненості за допомогою аналізу основних компонентів.
- Нас часто цікавлять коваріації та кореляції між алелями на різних локусах, порушення рівноваги зв'язків (LD).
- Коваріація між локусами (ЛД) може виникати між локусами з різних причин, зокрема структури популяції та домішки, як описано в розділі.
- Розпад ЛД внаслідок рекомбінації може бути змодельований і потенційно використаний на сьогоднішній день, коли LD був створений (наприклад, через домішки).
Втрату гетерозиготності через інбридинг можна розділити по статистиці F на декількох рівнях. Наприклад, ми можемо розділити загальний коефіцієнт інбридингу особини (\(F_{IT}\)) порівняно з популяцією між\(F_{IS}\) і\(F_{ST}\). Для наступних прикладів сценаріїв ви\(F_{IS}\) очікуєте бути більшим або меншим, ніж\(F_{ST}\)? Поясніть свою відповідь.
- Карла II, де субпопуляція - Іспанія, а загальна чисельність населення - європейці.
- Субпопуляції рослин, що живуть на схилі гори, де пилок розганяється на великі відстані за допомогою вітру, але особини самозапилюються близько 50% часу,
- Риби, які живуть в озерах з дуже мало доступних водних шляхів між озерами, але там, де риби вільно плавають в межах озер. Кожне озеро є субпопуляцією, а весь басейн озера - загальна чисельність населення.
У виду жука колір і форма крил контролюються двома різними поліморфізмами (з алелями великими/малими та червоними/жовтими відповідно). У музейній колекції ви оцінюєте частоту чотирьох гаплотипів:
| великий/червоний | великий/жовтий | малий/червоний | малий/жовтий |
| 0.69 | 0.00 | 0,09 | 0,22 |
Ця колекція з 60 років тому. У нинішніх популяціях ви оцінюєте частоту гаплотипів, щоб бути:
| 0.5452 | 0,148 | 0,2348 | 0.0752 |
- Якщо припустити одне покоління на рік, яка фракція рекомбінації між цими локусами?
- Якісно, як би змінилася ваша відповідь, якби ви визначили, що перетин відбувається лише у самок, а не у самців?