Skip to main content
LibreTexts - Ukrayinska

2: Частоти алелів та генотипів

  1. Last updated
  2. Save as PDF
  • Page ID
    7809

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    У цьому розділі ми попрацюємо над тим, як основи менделівської генетики грають на рівні популяції в статево розмножуються організмах.

    Локуси та алелі є основною валютою популяції генетики—і справді генетики. Локусом може бути цілий ген або одна нуклеотидна базова пара, така як A-T. У кожному локусі може бути кілька генетичних варіантів, що розділяються в популяції - ці різні генетичні варіанти відомі як алелі. Якщо всі особини в популяції несуть один і той же алель, ми говоримо, що локус мономорфний; у цього локусу відсутня генетична мінливість популяції. Якщо в популяції є множинні алелі в локусі, ми говоримо, що цей локус поліморфний (це іноді називають сегрегаційним місцем).

    Таблиця\(\PageIndex{1}\): Змінні сайти в екзонах 2 і 3 гена АДГ у дрозофіли Макдональд і Крейтмана (1991). Перший стовпець (поз.) дає позицію в гені; ексон 2 починається з позиції 778, і ми обрізали набір даних на сайті 1175. Другий стовпець дає консенсусний нуклеотид (con.), тобто найпоширенішу базу в цій позиції; особи з нуклеотидами, які відповідають консенсусу, позначені тире. Перші стовпці послідовності (a-l) — від D. melanogaster; наступні стовпці
    (a-f) дають послідовності з D. simulans, а остаточний набір стовпців (a-l) з D. yakuba. Останній стовпець показує, чи є різниця несинонімічною (N) або синонімічною (S) зміною.

    поз.

    кон.

    a

    б

    c

    d

    е

    f

    г

    ч

    я

    j

    к

    л

    		  

    a

    б

    c

    d

    е

    f

    		  

    a

    б

    c

    d

    е

    f

    г

    ч

    я

    j

    к

    л

    НС/С

    781

    Г

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    NS

    789

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    S

    808

    А

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    NS

    816

    Г

    Т

    Т

    Т

    Т

    -

    -

    -

    -

    -

    -

    -

    Т

    		  

    Т

    Т

    Т

    Т

    Т

    Т

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    S

    834

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    C

    C

    -

    -

    -

    C

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    S

    859

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    Г

    NS

    867

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    Г

    Г

    Г

    Г

    Г

    А

    Г

    Г

    Г

    Г

    Г

    Г

    S

    870

    C

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    Т

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    S

    950

    Г

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    А

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    S

    974

    Г

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    Т

    -

    Т

    Т

    Т

    Т

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    S

    983

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    S

    1019

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    А

    -

    -

    -

    -

    -

    -

    -

    S

    1031

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    А

    -

    -

    -

    S

    1034

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		    

    C

    C

    C

    C

    C

    -

    -

    C

    -

    C

    C

    S

    1043

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    А

    -

    -

    -

    -

    -

    -

    -

    S

    1068

    C

    Т

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    S

    1089

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    А

    А

    А

    А

    А

    А

    		  

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    NS

    1101

    Г

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    А

    А

    А

    А

    А

    А

    А

    А

    А

    А

    А

    А

    NS

    1127

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    S

    1131

    C

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    Т

    -

    -

    -

    -

    -

    -

    -

    S

    1160

    Т

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    -

    		  

    -

    -

    -

    -

    -

    -

    		  

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    C

    S

    Таблиця\ ref {Table:ADH} показує невеликий розтяг ортологічної послідовності для локусу АДГ із зразків з Drosophila melanogaster, D. simulans та D. yakuba. D. melanogaster і D. simulans є сестринськими видами, а D. yakuba є близькою групою до двох. Кожен стовпець представляє один гаплотип від індивіда (індивіди диплоїдні, але були інбредними, тому вони гомозиготні для свого гаплотипу). Показані лише ділянки, які відрізняються між особинами трьох видів. Сайт\(834\) є прикладом поліморфізму; деякі особини D. simulans несуть\(C\) алель, а інші мають\(T\). Фіксовані відмінності - це ділянки, які відрізняються між видами, але є мономорфними всередині виду. Сайт\(781\) є прикладом фіксованої різниці між D. melanogaster і двома іншими видами.

    Ми також можемо анотувати алелі та локуси різними способами. Наприклад, позиція\(781\) - це несинонімічна фіксована різниця. Ми називаємо менш поширеним алелем при поліморфізмі мінор алель і загальний аллель основним алелем, наприклад, на місці\(1068\)\(T\) алель є мінор аллель в D. melanogaster. Ми називаємо більш еволюційно недавній з двох алелів похідним алелем, а старший з двох - аллелем предків. Ми робимо висновок, що\(T\) алель на місці 1068 є похідним алелем, оскільки він\(C\) зустрічається в обох інших видах, припускаючи, що\(T\) алель виник через\(C \rightarrow T\) мутацію.

    Вправа\(\PageIndex{1}\)
    1. Скільки ділянок сегрегації має зразок D. simulans в гені ADH?
    2. Скільки фіксованих відмінностей існує між D. melanogaster і D. yakuba?

    Частоти алелів

    Частоти алелів є центральною одиницею аналізу популяційної генетики, але від диплоїдних особин ми отримуємо лише спостереження за підрахунками генотипів. Наше перше завдання - обчислити частоти алелів за підрахунками генотипів. Розглянемо диплоїдний аутосомний локус, що розділяє на два алелі (\(A_1\)і\(A_2\)). Ми будемо використовувати ці довільні мітки для наших алелів, просто щоб зберегти це загальне. Дозволяти\(N_{11}\) і\(N_{12}\) бути кількістю\(A_1A_1\) гомозигот і\(A_1A_2\) гетерозигот відповідно. Більш того, нехай\(N\) буде загальна кількість диплоїдних особин в популяції. Потім ми можемо визначити відносні\(A_1A_1\) частоти\(A_1A_2\) генотипів\(f_{11} = N_{11}/N\) і\(f_{12} = N_{12}/N\) відповідно. Частота алеля\(A_1\) в популяції потім задається

    \[p = \frac{2 N_{11} + N_{12}}{2N} = f_{11} + \frac{1}{2} f_{12}. \nonumber\]

    Зауважте, що це випливає безпосередньо з того, як ми підраховуємо алелі, задані генотипи людей, і тримається незалежно від пропорцій Харді — Вайнберга та рівноваги (розглянуто нижче). Частота альтернативного аллеля (\(A_2\)) тоді якраз\(q=1-p\).

    Заходи генетичної мінливості

    Нуклеотидна різноманітність (\(\pi\)) - Однією загальною мірою генетичного різноманіття є середня кількість одиночних нуклеотидних відмінностей між гаплотипами, вибраними випадковим чином із зразка. Це називається нуклеотидним різноманіттям і часто позначається\(\pi\). Наприклад, ми можемо обчислити\(\pi\) для нашого локусу ADH з таблиці\ ref {table:ADH} вище: у нас є 6 послідовностей з D. simulans (a-f), загалом існує 15 способів сполучення цих послідовностей, і

    \[\pi=\frac{1}{15} \big( (2 + 1 + 1 + 1 + 0 ) + (3 + 3 + 3 + 2 ) +(0 + 0 + 1) + (0 + 1) + (1) \big)=1.2\overline{6}\]

    де перший термін у дужках дає попарні відмінності між a та b-f, другий термін у дужках - відмінності між b та c-f тощо.

    Наша\(\pi\) міра буде залежати від довжини послідовності, для якої вона розрахована. Тому зазвичай\(\pi\) нормується довжина послідовності, яка повинна бути за ділянку (або на базу) міра. Наприклад, наша послідовність АДГ охоплює\(397\) bp ДНК і так\(\pi = 1.2\overline{6}/397=0.0032\) на ділянку в D. simulans для цього регіону. Зверніть увагу, що ми також могли б\(\pi\) обчислити для синонімічного сайту (або несинонімічного). Для синонімічного сайту\(\pi\) ми б підрахували кількість синонімічних відмінностей між нашими парами послідовностей, а потім розділимо на загальну кількість сайтів, де могла відбутися синонімічна зміна. Технічно нам потрібно було б розділити на загальну кількість можливих точкових мутацій, які призведуть до синонімічної зміни; це тому, що деякі мутаційні зміни на конкретному нуклеотиді призведуть до несинонімічної або синонімічної зміни залежно від зміни базової пари.

    Кількість сегрегаційних сайтів

    Іншою мірою генетичної мінливості є загальна кількість ділянок, які є поліморфними (сегрегуючими) у нашому зразку. Одне питання полягає в тому, що кількість сегрегаційних сайтів зростатиме, оскільки ми послідовно більше осіб (на відміну від\(\pi\)). Пізніше в курсі ми поговоримо про те, як стандартизувати кількість сегрегаційних сайтів за кількістю секвенованих осіб (див.\ ref {watterson_theta}).

    Частотний спектр

    Ми також часто хочемо зібрати інформацію про частоту алелей на різних сайтах. Ми називаємо алелями, які зустрічаються один раз у зразку синглтонів, алелями, які зустрічаються двічі в зразку дублетонів, і так далі. Ми підраховуємо кількість локусів, де аллель знайдений\(i\) раз з\(n\), наприклад, скільки синглтонів є в зразку, і це називається частотним спектром. Ми хочемо зробити це певним послідовним чином, наприклад, обчислення частотного спектру незначного алеля або похідного алеля.

    Вправа\(\PageIndex{2}\)

    Скільки синглетів незначних аллелів є в D. simulans в регіоні АДГ? [Визначення незначного аллеля тільки в межах D. simulans.]

    Рівні генетичної мінливості між видами

    Два спостереження спантеличили популяційних генетиків з моменту створення молекулярної популяційної генетики. Перший - відносно високий рівень генетичної варіації, що спостерігається у більшості обов'язково статевих видів. Це перше спостереження частково сприяло розвитку Нейтральної теорії молекулярної еволюції, ідеї про те, що значна частина цього молекулярного поліморфізму може просто відображати баланс між генетичним дрейфом і мутацією. Друге спостереження - відносно вузький діапазон поліморфізму серед видів із значно різними розмірами перепису. Це спостереження представляло загадку, оскільки нейтральна теорія передбачає, що рівні генетичного різноманіття повинні масштабуватися відповідно до чисельності популяції. Багато зусиль у теоретичній та емпіричній популяційній генетиці було присвячено спробі узгодити моделі з цими різними спостереженнями. Ми повернемося, щоб обговорити ці ідеї протягом нашого курсу.

    Перші спостереження молекулярно-генетичного різноманіття в природних популяціях були зроблені на основі досліджень даних аллоциму, але ми можемо переглянути ці загальні закономірності за допомогою сучасних даних. Наприклад, Leffler et al. (2012) зібрали дані про рівні всередині популяції, аутосомно-нуклеотидного різноманіття (π) для 167 видів через 14 філ з некодуючих та синонімічних сайтів (рис. 2.3). Видом з найнижчими рівнями π в їх обстеженні була Рись, причому π = 0,01%, тобто лише 1/10000 основ відрізнялися між двома послідовностями. На відміну від цього, деякі з найвищих рівнів різноманітності були знайдені в Ciona savignyi, Sea Squirts, де чудові основи 1/12 відрізняються між парами послідовностей. Цей 800-кратний діапазон різноманітності здається вражаючим, але розміри населення перепису мають набагато більший діапазон.

    21016139168_2a8a57ded3_z.jpg
    Малюнок\(\PageIndex{2}\): Сквирт (Ciona кишечник). Вступити в глибоку фізіологію та психологію. Льоб, Дж. 1899 р. Зображення з бібліотеки спадщини біорізноманіття. Надано бібліотекою MBLWHOI. Немає відомих обмежень щодо авторських прав.

    Пропорції Харді — Вайнберга

    Уявіть собі спаровування населення випадковим чином щодо генотипів, тобто відсутність інбридингу, асортативного спарювання, відсутність структури популяції та відсутність статевих відмінностей у частотах алелів. Частота алелей\(A_1\) у популяції в момент розмноження становить\(p\). \(A_1A_1\)Генотип створюється шляхом проникнення до нашої популяції та самостійного малювання двох\(A_1\) алельних гамет, щоб сформувати зиготу. Тому ймовірність того, що індивід є\(A_1A_1\) гомозиготою, є\(p^2\). Така ймовірність також є очікуваними частотами\(A_1A_1\) гомозиготи в популяції. Очікувана частота трьох можливих генотипів

    \(f_{11}\) \(f_{12}\) \(f_{22}\)
    \ (f_ {11}\)» style="вирівнювання тексту: центр; ">\(p^2\) \ (f_ {12}\)» style="вирівнювання тексту: центр; ">\(2pq\) \ (f_ {22}\)» style="вирівнювання тексту: центр; ">\(q^2\)

    тобто їх очікування Харді-Вайнберга. Зауважте, що нам потрібно лише припустити випадкове спаровування щодо нашого фокусного алелю, щоб ці очікувані частоти тримали в зиготах, що утворюють наступне покоління. Еволюційні сили, такі як селекція, змінюють частоти алелів протягом поколінь, але не змінюють цього очікування для нових зигот, поки\(p\) частота\(A_1\) алеля в популяції в той час, коли гамети зливаються. Нам потрібні лише припущення відсутності міграції, відбору та мутації для того, щоб ці очікування Генотипів Харді-Вайнберга представляли довгострокову рівновагу.

    Вправа\(\PageIndex{3}\)

    На прибережних островах Британської Колумбії зустрічається підвид чорного ведмедя (Ursus americanus kermodei, ведмідь Кермоде). Багато представників цього підвиду чорного ведмедя білі; їх іноді називають ведмедями-духами. Ці ведмеді не є гібридами з білими ведмедами, а також не альбіносами. Вони є гомозиготами для рецесивної зміни в гені MC1R. Особи, які\(GG\) перебувають на цьому SNP, білі, в той час як\(AA\) і\(AG\) особини чорні.

    Нижче наведено кількість генотипів для поліморфізму MC1R у зразку ведмедів із популяцій островів Британської Колумбії з.

    \(AA\) \(AG\) \(GG\)
    \ (AA\)» style="вирівнювання тексту: центр; ">42 \ (AG\)» style="вирівнювання тексту: центр; ">24 \ (GG\)» style="вирівнювання тексту: центр; "> 21

    Які очікувані частоти трьох генотипів під HW?

    EIiK2dsWoAAmUOf.jpeg
    Малюнок\(\PageIndex{1}\): Ведмідь Кермода (\ textit {Ursus americanus kermodei}). Цілком можливо, що цей морф є прихильним, оскільки лосось, який їдять ці ведмеді, важче бачити світловий морф\ citep {klinka2009adaptive}. Адаптивна цінність дегустації, як кориця, невідома. \ BHLNKC {Польова книга північноамериканських ссавців; описи кожного ссавця відомі на північ від Ріо-Гранде. Ентоні, (1928) Н. е.} {https://www.biodiversitylibrary.org/.../115/mode/1up}

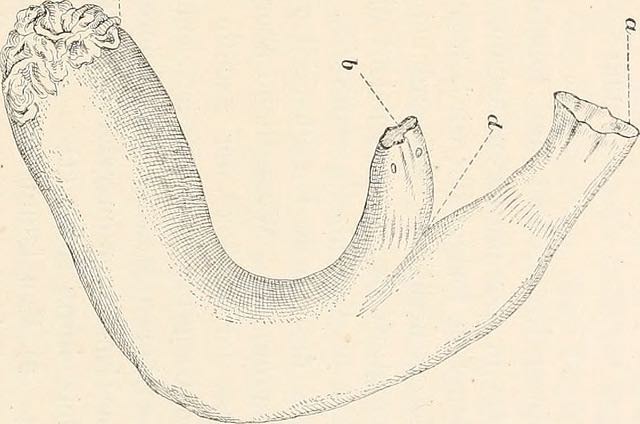
    Див. Рисунок\ ref {Fig:HWE_CEU_YRI} для гарної емпіричної демонстрації пропорцій Харді — Вайнберга. Середня частота кожного генотипу тісно відповідає його очікуванням HW, і значна частина розкиду точок навколо очікуваної лінії обумовлена нашим невеликим розміром вибірки (\(\sim 60\)особини). Хоча HW часто здається дурною моделлю, вона часто тримається надзвичайно добре в межах населення. Це тому, що люди не спаровуються випадково, але вони випадково спаровуються відносно свого генотипу в більшій частині локусів у геномі.

    Вправа\(\PageIndex{4}\)

    Ви досліджуєте локус з трьома алелями, A, B і C, з частотами\(p_A\) алелів\(p_B\), і\(p_C\). Яка частка населення, як очікується, буде гомозиготами при Харді — Вайнберзі?

    Мікросупутники - це області генома, де люди змінюються за кількістю копій деякої короткої ДНК повторюють, що вони несуть. Ці регіони часто сильно варіюються між окремими особами, що робить їх підходящим способом ідентифікації осіб із зразка ДНК. Цей так званий ДНК-дактилоскопічний друк має широкий спектр застосувань від встановлення батьківства та ідентифікації людських останків до зіставлення осіб із зразками ДНК з місця злочину. ФБР використовує базу даних CODIS. База даних CODIS містить генотипи понад 13 мільйонів людей, більшість з яких були засуджені за злочин. Більшість профілів фіксують генотипи на 13 мікросупутникових локусах, які є повтореннями тетрануклеотидів (з 2017 року генотипізовано 20 ділянок).

    Кількість алелів для двох локусів (D16S539 і TH01) наведено в таблиці\ ref {table:codis_1} і\ ref {table:codis_2} для вибірки з 155 осіб європейського походження. Можна припустити, що ці два локуси знаходяться на різних хромосомах.

    [таблиця: CODIS _1]

    [таблиця: CODIS _2]

    Вправа\(\PageIndex{5}\)

    Ви витягуєте зразок ДНК з місця злочину. Генотип становить 100/80 в локусі D16S539 і 70/93 при TH01.

    1. У вас є підозрюваний під вартою. Припускаючи, що цей підозрюваний невинний і має європейське походження, яка ймовірність того, що їх генотип випадково збігнеться з цим профілем (ймовірність помилкової відповідності)?
    2. ФБР використовує\(\geq\) 13 маркерів. Чому ця більша кількість необхідна для того, щоб заява про матч була переконливою доказами в суді?
    3. Ранній випадок, який викликав дискусії серед судових генетиків, був злочином серед Абенакі, індіанської громади у Вермонті. На місці злочину був зразок ДНК, і вважалося, що злочинець, ймовірно, є членом громади Абенакі. Враховуючи, що частоти алелів різняться між популяціями, чому люди будуть стурбовані використанням даних з населення, що не є абенакі, для обчислення ймовірності помилкової відповідності?

    асортативне спарювання

    Одним з основних порушень припущень Харді Вайнберга є невипадкове спарювання по відношенню до генотипу в локусі. Один із способів, яким люди можуть спаровуватися невипадково, - це якщо люди вирішують спаровуватися на основі фенотипу, визначеного (частково) генотипом у локусі. Це невипадкове спарювання може бути між: 1) особинами зі схожим фенотипом, так званим позитивним ассортативним спарюванням або 2) особинами з різнорідними фенотипами, негативним ассортативним спарюванням або дизасортативним спарюванням. Тут ми коротко обговоримо пару реальних прикладів асортативного спарювання, щоб переконатися, що ми всі на одній сторінці. У наступних кількох розділах ми зіткнемося з іншими формами невипадкового спарювання через інбридинг та структуру популяції.

    Демонстрація пропорцій Харді — Вайнберга за допомогою 10,000 SNP з європейського (CEU) та африканського (YRI) населення HapMap. У кожній з цих популяцій частота алелів проти частоти генотипів 3; кожен SNP представлений 3 різними кольоровими точками. Суцільні лінії показують середню частоту генотипу. Пунктирні лінії показують прогнозовану частоту генотипу з рівноваги Харді — Вайнберга. Повідомлення в блозі на малюнку тут.
    Малюнок\(\PageIndex{1}\): Демонстрація пропорцій Харді — Вайнберга за допомогою 10,000 SNP з європейського (CEU) та африканського (YRI) населення HapMap. У кожній з цих популяцій частота алелів проти частоти генотипів 3; кожен SNP представлений 3 різними кольоровими точками. Суцільні лінії показують середню частоту генотипу. Пунктирні лінії показують прогнозовану частоту генотипу з рівноваги Харді — Вайнберга. Код тут. Повідомлення в блозі на малюнку тут.

    Позитивне ассортативне спарювання на основі фенотипу може створити надлишок гомозигот. Метелики Heliconius славляться своєю мімікрією, де отруйні пари віддалено споріднених видів імітують яскраві кольорові візерунки один одного і тому поділяють переваги того, що їх уникають візуальні хижаки (мюллерські міміки). H. melpomene rosina та H. cydno chioneus є тісно спорідненими видами, які спільно зустрічаються в центральній Панамі, але імітують різні інші спільні види (рис.\ ref {рис:Heliconius_merrill_assort}). Ці відмінності в кольоровій структурі обумовлені кількома локусами з великими фенотипічними ефектами. Два види можуть гібридизувати та виробляти життєздатні гібриди F1. Ці гібриди F1 є гетерозиготами в кольорових локусах, і їх проміжний вигляд означає, що вони погані міміки, і тому їх швидко з'їдають хижаки. Однак ці гібриди гетерзиготи (F1) дуже рідкісні в природі\(< \frac{1}{1000}\), оскільки батьківські види демонструють сильне позитивне асортаційне спарювання на основі кольорового малюнка, заснованого на генетичних відмінностях у перевагах матів.

    Фенотипи малюнка крила зверху, H. cydno chioneus (зліва), H. melpomene rosina (праворуч), їх неміметичний гібрид першого покоління (центр); і знизу, їх симпатрічні комікси H. sapho sapho (зліва) та H. erato демофун (праворуч). Малюнок і підпис змінені з,.
    Малюнок\(\PageIndex{1}\): Фенотипи малюнка крила зверху, H. cydno chioneus (ліворуч), H. melpomene rosina (праворуч), їх неміметичний гібрид першого покоління (центр); і знизу, їх симпатрічні комікси H. sapho (зліва) та H. erato демофун ( праворуч). Малюнок та підпис змінені з Merrill
    et al. (2019), відповідно до CC BY 4.0.
    white_throated_sparrow.jpg
    Малюнок\(\PageIndex{1}\): Горобці білогорлі (Zonotrichia albicollis) з білим морфом (нижній, самець) і засмаглим морфом (верх, самка). Різниця між морфами не була повністю оцінена до 1960-х років\ citep {lowther1961polymorphism}, раніше пташини% https://www.audubon.org/news/the-fas...oated-sparrows думав, що загар морфи були тільки молоді або жіночі особини (тому чоловічі та жіночі етикетки Одюбона цілком можуть неправильно). Існує також ряд поведінкових відмінностей, причому обидві статі біло-смугастого морфа інвестують більше в територіальну оборону, а засмаглі смугасті морфи більше батьківської опіки.

    Диссортативне спарювання, спарювання несхожих особин, може привести до надлишку гетерозигот і дефіциту гомозигот. Один із прикладів дуже сильного дисортативного спарювання пропонують білоголові горобці (Zonotrichia albicollis). У білогорлих горобців зустрічається біло-смугастий і загар смугастий морф, при цьому жіночі і чоловічі біло-смугасті морфи мають набагато більш яскраву білу смугу і горло. У цій системі спостерігається дуже сильне дисортативне спаровування: 1099 з 1116 гніздових пар, що складаються з одного засмаги та одного біло-смугастого морфа, і лише 17 з цих гніздових пар є різними морфами. Різниця між цими морфами має простий візерунок успадкування, причому білий колір обумовлений одним домінуючим алелем (називається 2m) та кольором засмаги від рецесивного алеля під назвою 2. Таким чином, сильне дисортативне спарювання робить сильний вплив на частоти генотипу:

    Отже Білий (Супер) Білий
    2/2 2/2м 2м/2м
    978 1011 3

    Майже немає 2m гомозигот (так звані супер білі особини), незважаючи на те, що алель 2m є поширеним у популяції (дані Tuttle et al., 2016, таблиця S1).

    Ще одним важливим прикладом дисортативного спарювання є системи типу спарювання, які присутні у багатьох грибів, водоростей та найпростіших. Гамети одного виду можуть зливатися, утворюючи зиготу лише в тому випадку, якщо вони відрізняються за типом спарювання. Тип спарювання гамет генетично контролюється локусом типу спаровування, і тому особини майже завжди гетерозиготні в цьому місці. У деяких групах організмів існує відразу два різних алелі, в інших кладах ці локуси мають десятки або сотні алелів.

    1280px-Sparassis_crispa_JPG1.jpg
    Малюнок\(\PageIndex{9}\): Гриби цвітної капусти (Sparassis crispa) паразитують на коренях дерев і утворюють ці дивовижні, їстівні плодові тіла, які можуть важити до 30 фунтів і, мабуть,
    на смак як локшина. У колекції з 18 плодових тіл з популяції Спарасіса всі особини були гетерозиготами за типом спарювання і генетично ідентифіковано 17 різних типів спарювання (James, 2015; Martin and Gilbertson, 1978). (CC BY-SA 3.0; CC BY 3.0 через Вікіпедію)

    Обмін алелями між пов'язаними особами та ідентичністю за походженням

    Всі особини в популяції пов'язані один з одним гігантським родоводом (генеалогічним древом). Для більшості пар осіб у популяції ці відносини дуже віддалені (наприклад, далекі двоюрідні брати), тоді як деякі особи будуть більш тісно пов'язані між собою (наприклад, брати/перші двоюрідні брати і сестри). Всі люди пов'язані один з одним різним рівнем спорідненості або спорідненості. Пов'язані особи можуть ділитися алелями, які обидва походять від спільного спільного предка. Щоб бути спільними, ці алелі повинні бути успадковані через всі мейози, що з'єднують двох осіб (наприклад, вижити\(\frac{1}{2}\) ймовірність сегрегації кожного мейозу). Оскільки близькі родичі розділені меншою кількістю мейозів, більш близькі родичі поділяють більше алелів. На малюнку\ ref {Fig:IBD_cousins_chr_cartoon} ми показуємо спільне використання хромосомних областей між двома двоюрідними братами. Як ми побачимо, багато популяційних та кількісних генетичних концепцій покладаються на те, наскільки тісно пов'язані люди, і тому нам потрібен певний спосіб кількісної оцінки ступеня спорідненості між людьми.

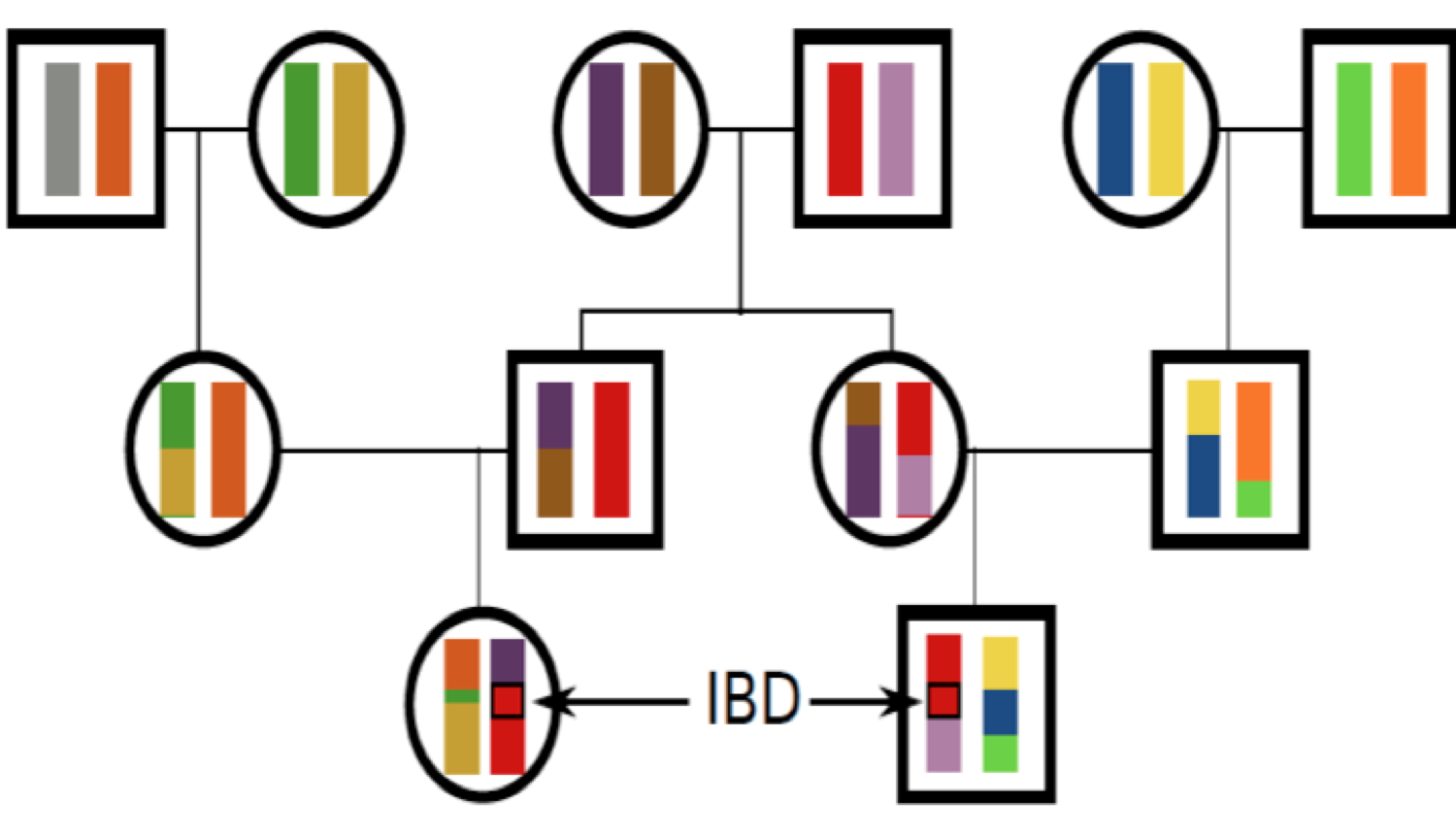
    Cousins_IBD_chromo_cartoon.png
    Перші двоюрідні брати поділяють розтягнення хромосоми, ідентичної за походженням. Різні диплоїдні хромосоми бабусь і батьків пофарбовані, щоб ми могли відстежувати їх і рекомбінації між ними протягом поколінь. Зверніть увагу, що ідентичність за походженням між двоюрідними братами зберігається протягом тривалого розтягування хромосоми через обмежену кількість поколінь для рекомбінації. Квадрати зображують самців і кола самок.

    Ми визначимо два алелі, щоб бути ідентичними за спуском (IBD), якщо вони ідентичні через передачу від спільного предка за останні кілька поколінь. На даний момент ми ігноруємо мутацію, і ми будемо точніше про те, що ми маємо на увазі під «минулими кількома поколіннями» пізніше. Наприклад, батько і дитина поділяють рівно один аллель, ідентичний за походженням в локусі, припускаючи, що два батьки дитини - випадково спарені особини з популяції. На малюнку\ ref {Fig:IBD_Cousins_cartoon} я показую родовід, що демонструє деякі конфігурації IBD.

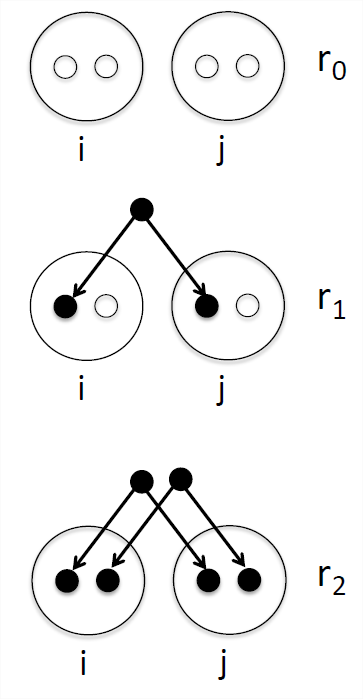
    clipboard_e6f734424a272a624fadfbe61a2b5a1b5.png
    Рисунок\(\PageIndex{1}\): Пара диплоїдних осіб (i та j), які поділяють 0, 1 або 2 алелі IBD, де рядки показують поділ алелів за походженням (наприклад, від спільного предка).}

    Одне резюме того, як пов'язані дві особи (назвемо їх\(i\) і\(j\)) є ймовірність того, що наша пара осіб поділяє 0, 1 або 2 алелі однакові за походженням (див. Рис.\ ref {рис:IBD_0_1_2}). Ми позначимо ці імовірності тотожності за\(r_0\) ступенем\(r_1\), і\(r_2\) відповідно. Див. розділ Таблиця\ ref {table:IBDProbs} для деяких прикладів. Ми також можемо інтерпретувати ці ймовірності як середні показники генома. Наприклад, в середньому на чверть всіх їх аутосомних локусів full-sibs поділяють нульові алелі, ідентичні за спуском.

    Одне резюме спорідненості, яке буде важливим, - це ймовірність того, що два алелі (I & J) вибрані випадковим чином, по одному з кожної з двох різних осіб\(i\) і\(j\), ідентичні за сходженням (\(P(\text{I\&J IBD})\)). Ми називаємо цю величину коефіцієнтом спорідненості індивідів\(i\) і\(j\), і позначимо її по\(F_{ij}\). Він розраховується як

    \[\begin{aligned} F_{ij} = & \mathbb{P}(\text{I\&J IBD} )\\ =& \mathbb{P}(\text{I\&J IBD} |~ \text{i\&j 0 IBD}) \mathbb{P}(\text{i\&j 0 IBD}) \nonumber\\ & + \mathbb{P}(\text{I\&J IBD} |~ \text{i\&j 1 IBD}) \mathbb{P}(\text{i\&j 1 IBD}) \nonumber\\ &+ \mathbb{P}(\text{I\&J IBD} |~ \text{i\&j 2 IBD}) \mathbb{P}(\text{i\&j 2 IBD}) \label{eqn:coeffkinship_step}\\ = & 0 \times r_0 + \frac{1}{4} r_1 + \frac{1}{2} r_2. \label{eqn:coeffkinship}\end{aligned}\]

    На наведеному вище кроці,\ ref {eqn:coeffkinship_step}, ми підсумовуємо умовну ймовірність алелей\(I\) &\(J\) бути IBD над тим, чи наші особи\(i\) &\(j\) частка\(0\)\(1\), або \(2\)алелі IBD, приклад використання Закону повної ймовірності (див. Додаток\ ref {eqn:law_tot_prob}). Тоді ми, в\ ref {eqn:coefffinship}, використали той факт, що ми можемо обчислити наші ймовірності стану I & J бути IBD, використовуючи правила передачі Менделя. Розглянемо ймовірність\(P(\text{I\&J IBD} |~ \text{i\&j 1 IBD})\), тобто, що наша пара алелів (\(I\)&\(J\)) витягнута з окремих осіб\(i\) і\(j\) є IBD, враховуючи це,\(i\) і\(j\) поділяють один алель IBD, це так\(\frac{1}{4}\) як нам потрібно намалювати алель, який є IBD з обох\(i\) і\(j\), тобто малювання обох чорних алелів на середній панелі Figure\ ref {рис:IBD_0_1_2}, що відбувається з ймовірністю\(\frac{1}{2} \times \frac{1}{2}\). Коефіцієнт спорідненості буде з'являтися кілька разів, як в нашому обговоренні інбридингу, так і в контексті фенотипічної подібності між родичами.

    Відносини (i, j)\(^{*}\) \(\mathbb{P}(\text{i\&j 0 IBD})\) \(\mathbb{P}(\text{i\&j 1 IBD})\) \(P(\text{i\&j 2 IBD})\) \(\mathbb{P}(\text{I\&J IBD} )\)
    \ (^ {*}\)» style="вирівнювання тексту: ліворуч; "> Відносини (i, j)\(^{*}\) \ (\ mathbb {P} (\ текст {i\ &j 0 IBD})\)» стиль = "вирівнювання тексту: центр; ">\(r_0\) \ (\ mathbb {P} (\ текст {i\ &j 1 IBD})\)» стиль = "вирівнювання тексту: центр; ">\(r_1\) \ (P (\ text {i\ &j 2 IBD})\)» style="вирівнювання тексту: центр; ">\(r_2\) \ (\ mathbb {P} (\ текст {I\ &J IBD})\)» стиль="вирівнювання тексту: центр; ">\(F_{ij}\)
    \ (^ {*}\)» style="вирівнювання тексту: ліворуч; "> батько — дитина \ (\ mathbb {P} (\ текст {i\ &j 0 IBD})\)» стиль = "вирівнювання тексту: центр; "> 0 \ (\ mathbb {P} (\ текст {i\ &j 1 IBD})\)» стиль = "вирівнювання тексту: центр; "> 1 \ (P (\ text {i\ &j 2 IBD})\)» style="вирівнювання тексту: центр; ">0 \ (\ mathbb {P} (\ текст {I\ &J IBD})\)» стиль = "вирівнювання тексту: центр; ">
    \ (^ {*}\)» style="вирівнювання тексту: ліворуч; "> повні брати і сестри \ (\ mathbb {P} (\ текст {i\ &j 0 IBD})\)» стиль = "вирівнювання тексту: центр; "> \ (\ mathbb {P} (\ текст {i\ &j 1 IBD})\)» стиль = "вирівнювання тексту: центр; "> \ (P (\ text {i\ &j 2 IBD})\)» style="вирівнювання тексту: центр; "> \ (\ mathbb {P} (\ текст {I\ &J IBD})\)» стиль = "вирівнювання тексту: центр; ">
    \ (^ {*}\)» style="вирівнювання тексту: ліворуч; "> Монозиготні близнюки \ (\ mathbb {P} (\ текст {i\ &j 0 IBD})\)» стиль = "вирівнювання тексту: центр; "> 0 \ (\ mathbb {P} (\ текст {i\ &j 1 IBD})\)» стиль = "вирівнювання тексту: центр; "> 0 \ (P (\ text {i\ &j 2 IBD})\)» style="вирівнювання тексту: центр; "> 1 \ (\ mathbb {P} (\ текст {I\ &J IBD})\)» стиль = "вирівнювання тексту: центр; ">
    \ (^ {*}\)» style="вирівнювання тексту: ліворуч; ">\(1^{st}\) двоюрідні брати \ (\ mathbb {P} (\ текст {i\ &j 0 IBD})\)» стиль = "вирівнювання тексту: центр; "> \ (\ mathbb {P} (\ текст {i\ &j 1 IBD})\)» стиль = "вирівнювання тексту: центр; "> \ (P (\ text {i\ &j 2 IBD})\)» style="вирівнювання тексту: центр; ">0 \ (\ mathbb {P} (\ текст {I\ &J IBD})\)» стиль = "вирівнювання тексту: центр; ">
    Вправа\(\PageIndex{6}\)

    Що таке\(r_0\)\(r_1\), і\(r_2\) для\(\frac{1}{2}\) братів? (\(\frac{1}{2}\)Сіби поділяють одного з батьків, але не іншого).

    Вправа\(\PageIndex{7}\)

    Поясніть словами чому\(\mathbb{P}(\text{I\&J IBD} |~ \text{i\&j 2 IBD}) = \frac{1}{2}\).

    Генотипічний розподіл між парами особин.

    Наші\(r\) коефіцієнти будуть мати різне використання. Наприклад, вони дозволяють обчислити ймовірність генотипів пари родичів. Розглянемо біаллельний локус, де алель\(A_1\) знаходиться на частоті\(p\), і двох осіб, які мають імовірності спільного використання алелів IBD\(r_0\),\(r_1\),\(r_2\). Яка загальна ймовірність того, що ці дві особи є гомозиготними для аллеля 1? Ну ось

    \[\begin{aligned} \mathbb{P}(\textrm{both } A_1 A_1) = & \mathbb{P}(\textrm{both } A_1 A_1 | 0 \text{ alleles } \mathrm{IBD}) \mathbb{P}(0 \text{ alleles } \mathrm{IBD}) \nonumber\\ & + \mathbb{P}(\textrm{both } A_1 A_1 | 1 \text{ allele }IBD) \mathbb{P}(1\text{ allele }IBD) \nonumber\\ &+ \mathbb{P}(\textrm{both } A_1 A_1 | 2 \text{ alleles }IBD) \mathbb{P}(2\text{ alleles }IBD)\end{aligned}\]

    Або, в нашому\(r_0\)\(r_1\),\(r_2\) позначення:

    \[\begin{aligned} \mathbb{P}(\textrm{both } A_1 A_1) = & \mathbb{P}(\textrm{both } A_1 A_1 | \textrm{0 alleles IBD}) r_0 \nonumber\\ & + \mathbb{P}(\textrm{both } A_1 A_1 | \textrm{1 alleles IBD}) r_1 \nonumber\\ & + \mathbb{P}(\textrm{both } A_1 A_1 | \textrm{2 alleles IBD}) r_2 \label{eqn:initial_relly_IBD_calc}\end{aligned}\]

    Якщо наша пара родичів поділяють\(0\) алелі IBD, то ймовірність того, що вони обидва гомозиготні\(\mathbb{P}(\textrm{both } A_1 A_1 | \text{0 alleles IBD}) =p^2 \times p^2\), є, оскільки всі чотири алелі представляють незалежні малюнки з популяції. Якщо вони поділяють\(1\) алель IBD, то спільний алель має тип\(A_1\) з ймовірністю\(p\), а потім інший не-IBD алель, у обох родичів, також повинен бути,\(A_1\) що відбувається з ймовірністю\(p^2\), тому \(\mathbb{P}(\textrm{both } A_1 A_1 | \text{1 alleles IBD})=p \times p^2\). Нарешті, наша пара родичів може розділити два алелі IBD, в цьому випадку\(\mathbb{P}(\textrm{both } A_1 A_1 | \text{2 alleles IBD}) = p^2\), тому що якщо один з наших особин гомозиготний для\(A_1\) алеля, обидві особи будуть. Збираючи це все разом, наш\ ref {eqn:initial_relly_IBD_Calc} стає

    \[\mathbb{P}(\textrm{both } A_1 A_1) = p^4 r_0 + p^3 r_1 + p^2 r_2 \label{eqn:IBD_relly_calc}\]

    Зауважте, що для конкретних випадків ми також могли б обчислити це, підсумовуючи всі можливі генотипи, які мали їхні спільні предки; однак це було б набагато більше, а не настільки загальним, як форма, яку ми вивели тут.

    Ми можемо виписати такі терміни, як\ ref {EQN:IBD_Relly_Calc} для всіх можливих конфігурацій обміну генотипу/неспільного використання між парою особин. Виходячи з цього, ми можемо записати очікувану кількість поліморфних ділянок, де наші особини поділяють 0, 1 або 2 алелі.

    Вправа\(\PageIndex{8}\): Trickier question

    Генотип нашого підозрюваного в питанні\ ref {Q:CODIS} виявляється 100/80 для D16S539 і 70/80 при TH01. Підозрюваний не відповідає ДНК з місця злочину; однак, вони можуть бути братом і сестрами.Обчисліть спільну ймовірність спостереження генотипу від злочину і нашого підозрюваного:

    1. Припускаючи, що вони не мають близьких стосунків.
    2. Припускаючи, що вони повні сиби.
    3. Коротко поясніть свої висновки.

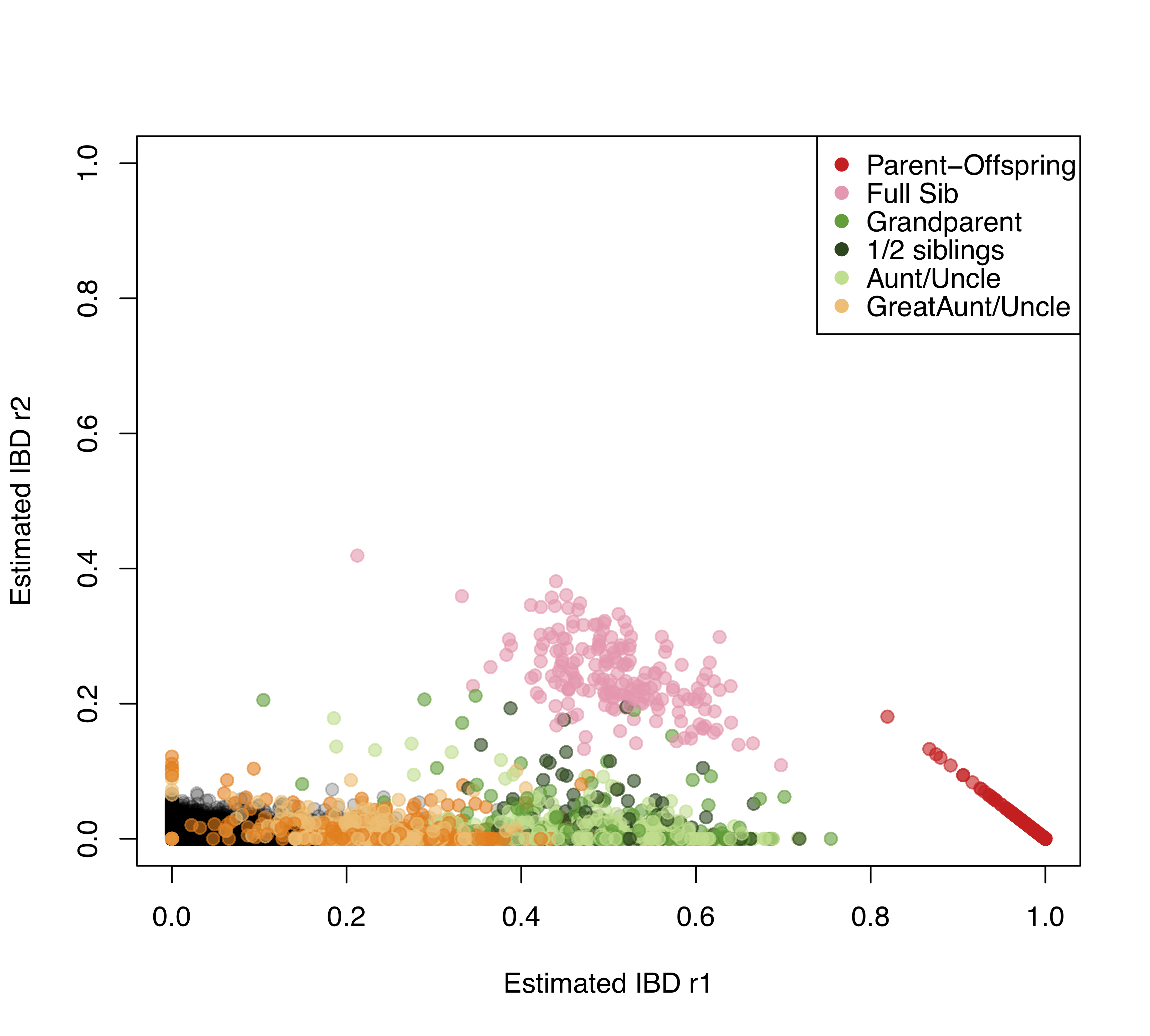
    Існує безліч способів оцінки відносин між людьми за допомогою генетичних даних. Приклад використання обміну алелями для ідентифікації родичів пропонується роботою Ненсі Чен. зібрала дані генотипування з тисяч Florida Scrub Jays в більш ніж десяти тисячах локусів. Ці сойки живуть на польовому майданчику Арчболда, і протягом багатьох десятиліть ретельно контролюються, дозволяючи знати родовід багатьох птахів. Використовуючи ці дані, вона оцінює частоти алелів у кожному локусі. Потім, прирівнюючи спостережуване число разів\(0\), яке поділяє пара особин\(1\)\(2\), або алелей до теоретичного очікування, вона оцінює ймовірність\(r_0\)\(r_1\), і\(r_2\) для кожна пара птахів. Сюжет з них наведено на малюнку\ ref {fig:FSJ_IBD}, показуючи, наскільки добре оцінки відповідають відомим з родоводу.

    FSJ_IBD.png
    Розрахунковий коефіцієнт спорідненості від Флориди Скраб Джейс. Кожна точка являє собою пару особин, побудованих за їх оцінками IBD (\(r_1\)і\(r_2\)) з їх генетичних даних. Точки пофарбовані їхніми відомими родоводами. Зверніть увагу, що більшість пар мають низьку спорідненість і не мають недавніх генеалогічних зв'язків, і так виглядають як чорні точки в нижньому лівому куті. Дякуємо Ненсі Чен за надання даних.

    Розподіл геномних блоків між родичами

    Ми можемо більш безпосередньо бачити спільне використання генома між близькими родичами, використовуючи масиви генотипування SNP високої щільності. На малюнку\ ref {Fig:First_Cousin_IBD} ми показуємо моделювання геномного обміну першими двоюрідними братами від їхньої спільної бабусі. Кольорові фіолетові - це регіони, де вони мають відповідний геномний матеріал, через те, що успадкували його IBD від своєї спільної бабусі.

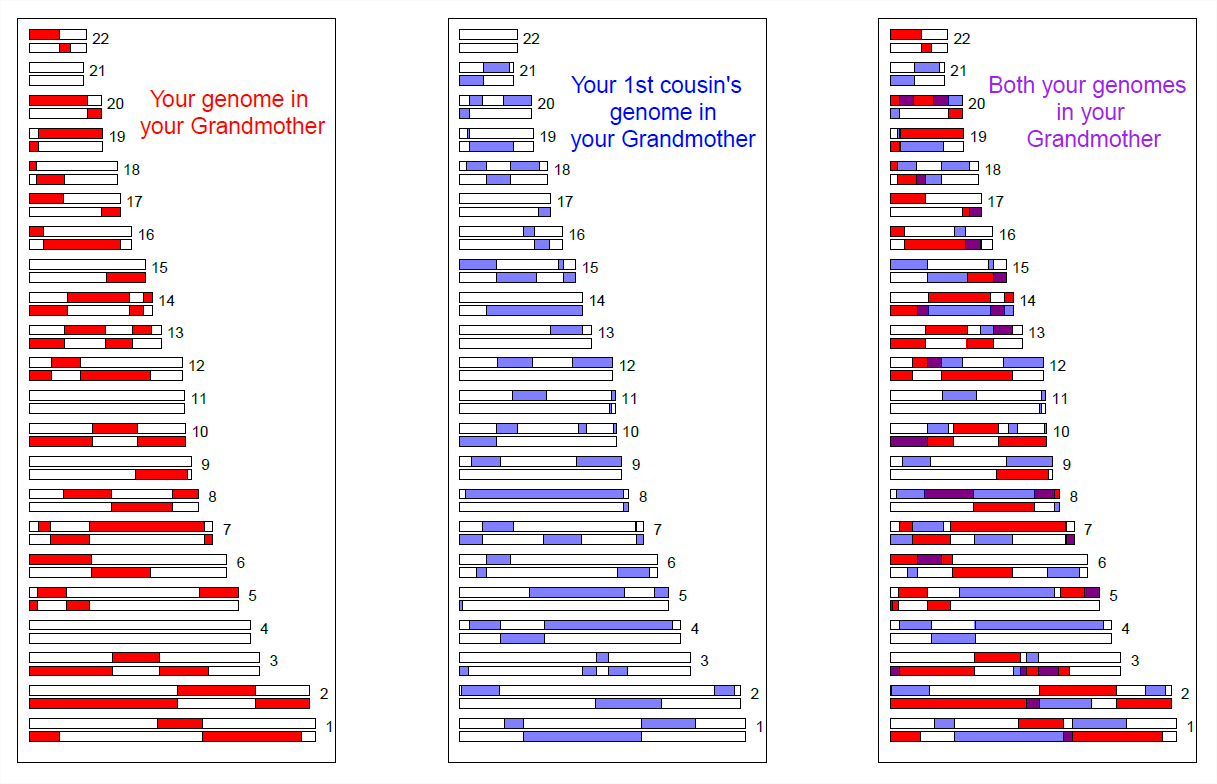
    clipboard_e7588ca2db7671fc214dbc8def71b7332.png
    Моделювання спільного використання між першими двоюрідними братами. Регіони 22 аутосом вашої бабусі, які ви успадкували, пофарбовані в червоний колір, ті, що ваші двоюрідні брати успадкували, пофарбовані в синій колір. На третій панелі ми показуємо перекриваються геномні області фіолетовим кольором, ці регіони будуть IBD у вас та вашого двоюрідного брата. Якщо ви повні двоюрідні брати, у вас також будуть спільні геномні регіони від вашого спільного діда, не показані тут. Детально про те, як ми зробили ці симуляції тут.

    Перші двоюрідні брати поділять принаймні один алель вашого генотипу на всіх поліморфних локусах у цих фіолетових регіонах. Існує цілий ряд методів виявлення такого обміну. Один із способів - шукати надзвичайно довгі ділянки генома, де дві особини ніколи не гомозиготні для різних алелів. Виявляючи пари особин, які поділяють незвично велику кількість таких передбачуваних блоків IBD, ми можемо сподіватися виявити невідомих родичів у наборах даних генотипування. Насправді такі компанії, як 23&me та Ancestry.com, використовують сигнали IBD, щоб допомогти визначити сімейні зв'язки.

    Як інший приклад розглянемо випадок третіх двоюрідних братів. Ви ділитеся одним з восьми наборів пра-прабабусь і дідусів з кожним з ваших (ймовірно, багатьох) третіх двоюрідних братів. В середньому ви і кожен з ваших третіх двоюрідних братів успадковуєте одну шістнадцяту частину вашого геному від кожного з цих двох прапрабабусь і дідусів. Це, виявляється, означає, що в середньому трохи менше одного відсотка геномів вашого та вашого третього двоюрідного брата (\(2 \times (1/16)^2 =0.78\%\)) будуть ідентичними в силу походження від цих спільних предків. Змодельований приклад, коли треті двоюрідні брати поділяють блоки свого генома (на хромосомі 16 і 2) завдяки своїй прапрабабусі, показаний на малюнку\ ref {fig:third_cousin_IBD}.

    Third_cousin_overlap_1.png
    Моделювання спільного використання між третіми двоюрідними братами, деталі такі ж, як на малюнку\ ref {Fig:First_Cousin_IBD}.

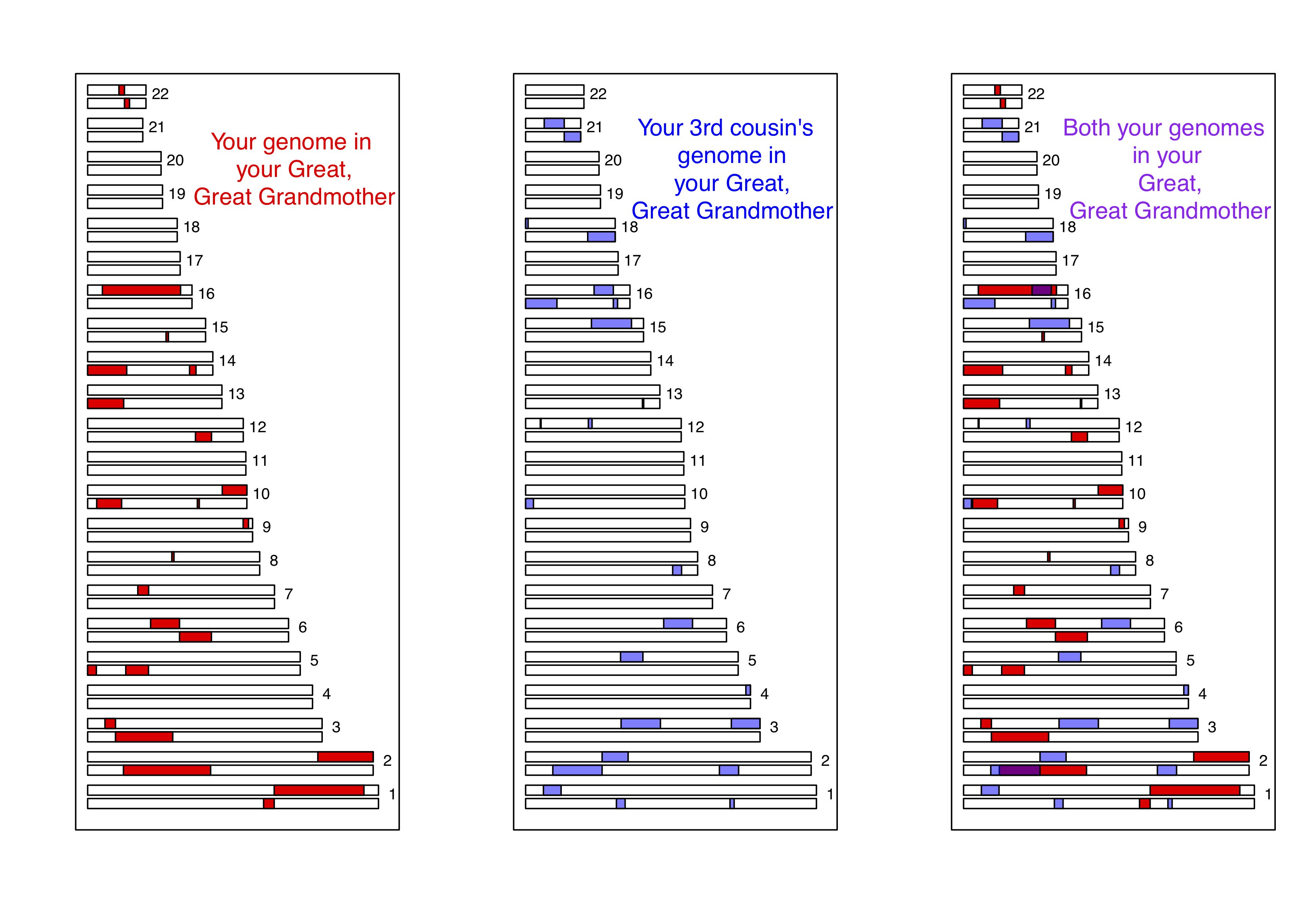
    Зверніть увагу, як якщо ви порівнюєте рис\ ref {Fig:Third_cousin_IBD} і Figure\ ref {Fig:First_Cousin_IBD}, люди успадковують менше IBD від спільної прапрабабусі, ніж від спільної бабусі, оскільки вони успадковують від більшої кількості предків далі. Також зверніть увагу, як обмін відбувається в коротших геномних блоках, оскільки він пройшов через більше поколінь рекомбінації під час мейозу. Ці блоки все ще виявляються, і тому треті двоюрідні брати можуть бути виявлені за допомогою мікросхем генотипування високої щільності, що дозволяє ідентифікувати більш віддалених родичів, ніж одні маркерні методи поодинці. Більш віддалені відносини, ніж треті двоюрідні брати, наприклад, четверті двоюрідні брати, починають мати значну ймовірність поділу жоден з їхнього генома IBD. Але у вас є багато четвертих двоюрідних братів, тому ви поділитеся деякими з вашого геному IBD з деякими з них; однак, стає все важче визначити ступінь спорідненості з генетичних даних, чим глибше в генеалогічному древі цей обмін йде.

    Інбридинг

    Ми можемо визначити інбредну особу як особу, батьки якої тісніше пов'язані один з одним, ніж дві випадкові особи, взяті з якоїсь еталонної популяції.

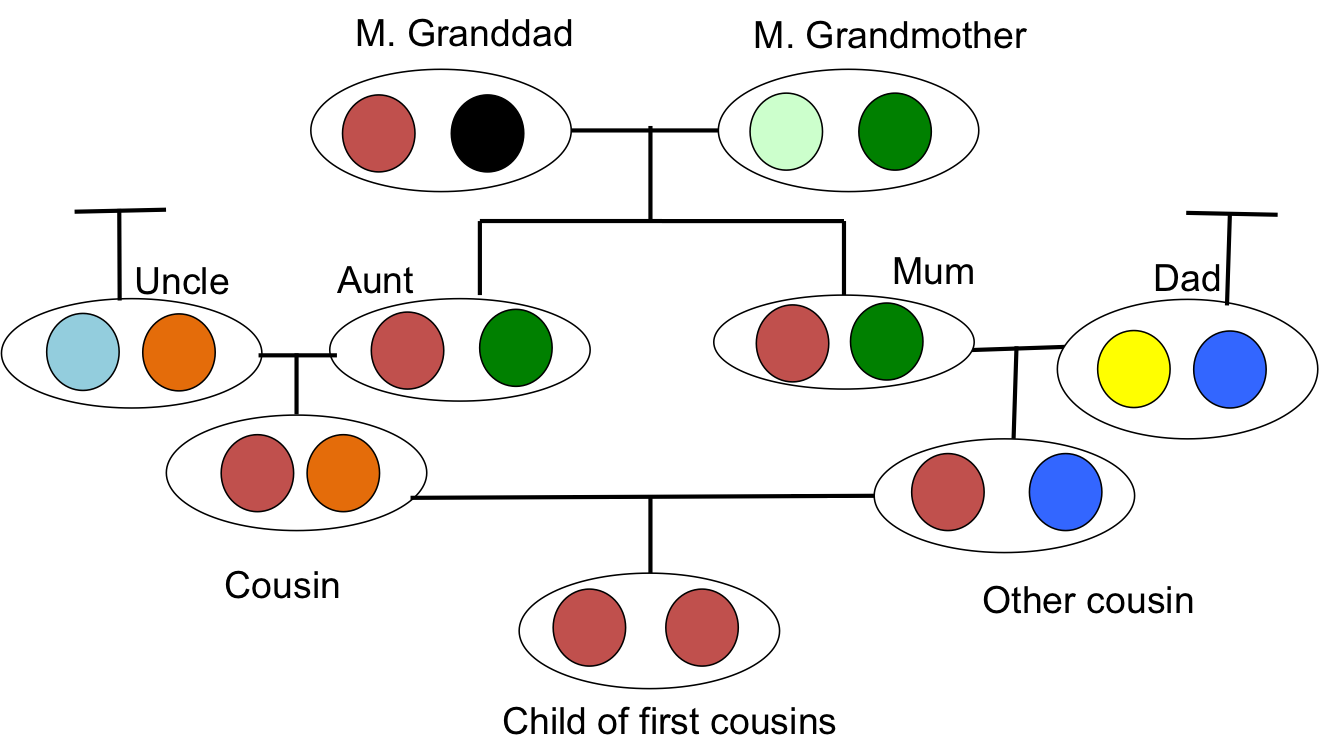
    Child_first_cousins_Homozy_BD.png
    Малюнок\(\PageIndex{1}\): Алелі передаються через інбредний родовід. Дві сестри (мама і тітка) поділяють два алелі, однакові за походженням (IBD). Двоюрідні брати поділяють один алель IBD. Потомство перших двоюрідних братів гомозиготне за спуском на цьому місці.

    Коли дві споріднених особини виробляють потомство, ця особина може отримати два алелі, однакові за походженням, тобто вони можуть бути гомозиготними за походженням (іноді їх називають аутозиготними), через те, що вони мають дві копії алеля різними шляхами через родовід. Така підвищена ймовірність бути гомозиготним щодо безпородної особини є найбільш очевидним ефектом інбридингу. Це також той, який буде нам найбільше цікавий, оскільки він лежить в основі багатьох наших уявлень про інбридингову депресію та структуру населення. Наприклад, на малюнку\ ref {fig:IBD_Cousins_Cartoon} наше потомство перших двоюрідних братів гомозиготно за походженням, отримавши один і той же алель IBD двома різними шляхами навколо петлі інбридингу.

    Оскільки потомство отримує випадковий алель від кожного з батьків (\(i\)і\(j\)), ймовірність того, що ці два алелі ідентичні за походженням, дорівнює\(F_{ij}\) коефіцієнту спорідненості двох батьків (\ ref {eqn:coeffkinship}). Це випливає з того, що генотип потомства проводиться шляхом вибірки алеля навмання у кожного з наших батьків.

    Узагальнений Харді — Вайнберг. Скинули індекси\(i\) і\(j\) для простоти.
    \(f_{11}\) \(f_{12}\) \(f_{22}\)
    \ (f_ {11}\)» style="вирівнювання тексту: центр; ">\((1-F) p^2 + F p\) \ (f_ {12}\)» style="вирівнювання тексту: центр; ">\((1-F) 2pq\) \ (f_ {22}\)» style="вирівнювання тексту: центр; ">\((1-F) q^2 + F q\)

    Єдиний спосіб, яким потомство може бути гетерозиготним (\(A_1 A_2\)) - це якщо їх два алелі в локусі не є ВБД (інакше вони обов'язково були б гомозиготними). Тому ймовірність того, що вони гетерозиготні, становить

    \[\mathbb{P}(A_1 A_2) = \mathbb{P}(A_1 A_2 |\textrm{I \& J not IBD} ) \P (\textrm{I \& J not IBD} ) = 2p q (1-F_{ij}) , \label{eq:hetGenHW}\]

    Потомство може бути гомозиготним для\(A_1\) алеля двома різними способами. Вони можуть мати два не-ІБД алелі, які не є IBD, але трапляються алельного типу\(A_1\), або їх два алелі можуть бути IBD, таким чином, що вони успадкували алель двома\(A_1\) різними шляхами від одного і того ж предка. Таким чином, ймовірність того, що потомство\(A_1\) гомозиготне для

    \[\begin{aligned} P(A_1 A_1) & = \mathbb{P}(A_1 A_1 |\textrm{I \& J not IBD} ) \P (\textrm{I\&J not IBD} ) + \mathbb{P}(A_1 A_1 |\textrm{I\&J IBD} ) \P (\textrm{I\&J IBD}) \nonumber\\ &= p^2(1-F_{ij}) + pF_{ij}.\end{aligned}\]

    за допомогою Закону повної ймовірності (див. Додаток\ ref {eqn:law_tot_prob}). Тому частоти трьох можливих генотипів можна записати, як наведено в таблиці\ ref {Table:generalizedHWE}, яка забезпечує узагальнення пропорцій Харді — Вайнберга.

    Вправа\(\PageIndex{9}\)

    Частота\(A_1\) алеля знаходиться\(p\) в біаллельному локусі. Припустимо, що наша популяція випадково спаровується і що частоти генотипу в популяції слідують від HW. Ми вибираємо дві особини навмання, щоб спаровуватися з цієї популяції. Потім ми спаровуємо дітей з цього хреста. Яка ймовірність того, що дитина від цього повного сіб-парування гомозиготний?

    Кілька петель інбридингу в родоводу

    До цього моменту ми припускали, що в недавній сімейній історії наших людей існує щонайменше один цикл інбридингу, тобто батьки нашої інбредної особистості мають щонайменше один недавній генеалогічний зв'язок. Однак людина, яка має кілька петель інбридингу у своєму родоводу, може бути гомозиготною за спуском завдяки отриманню алелів IBD через кілька різних петель. Щоб обчислити інбридинг у родоводах довільної складності, ми можемо вийти за межі наших початкових коефіцієнтів\(r_0\) спорідненості та\(r_2\) враховувати більш високий порядок розподілу алелів IBD між родичами.\(r_1\) Наприклад, ми можемо запитати, яка ймовірність того, що обидва алелі у першої особини поділяють IBD з одним алелем у другого індивіда? Всього існує дев'ять можливих коефіцієнтів спорідненості, щоб повністю описати спорідненість між двома диплоїдними особами, і ми не будемо йти до них тут, оскільки це багато, щоб відстежувати. Однак ми покажемо, як ми можемо розрахувати коефіцієнт інбридингу особини з множинними петлями інбридингу більш безпосередньо.

    Скажімо, батьки нашої інбредної особистості (B і C) мають\(K\) спільних предків, тобто осіб, які з'являються як в недавніх родинних деревах B, так і C. Ми позначаємо цих спільних предків по\(A_1, \dots,A_K\), і позначаємо загальною кількістю особин в ланцюжку від B до C через предка\(A_i\), включаючи B, C, і\(A_i\).\(n\) Наприклад, якщо B - тітка С, то B і C поділяють двох предків, які є батьками Б і, що еквівалентно, бабусями і дідусями С. У цьому випадку існує n = 4 особини від B до C через кожного з цих двох спільних предків. У загальному випадку коефіцієнт спорідненості В і С, тобто коефіцієнт інбридингу їх дитини, дорівнює

    \[F = \sum_{i=1}^K \frac{1}{2^{n_i}} \big( 1+ f_{A_i} \big) \label{eqn:inbreeding_over_ancs}\]

    де\(f_{A_i}\) - коефіцієнт інбридингу предка\(A_i\). Те, що тут відбувається, полягає в тому, що ми підсумовуємо всі взаємовиключні шляхи в родоводу, через які B і C можуть ділитися алелем IBD. Імовірно\(\frac{1}{2^{n_i}}\), пара алелів, відібраних випадковим чином від B і C, походить від одного і того ж родового алеля в особі\(A_i\), і в цьому випадку алелі є IBD. Однак, навіть якщо B успадковує материнський алель, а C успадковує батьківський алель спільного предка\(A_i\), якщо він сам\(A_i\) був інбредним, з ймовірністю\(f_{A_i}\) ці два алелі самі по собі IBD. Таким чином, спільний інбредний предок ще більше збільшує спорідненість B і C.

    Carlos_segundo80.png
    Родовід короля Іспанії Карла II. (Громадське надбання; Lec CRP1 від Вікімедіа)

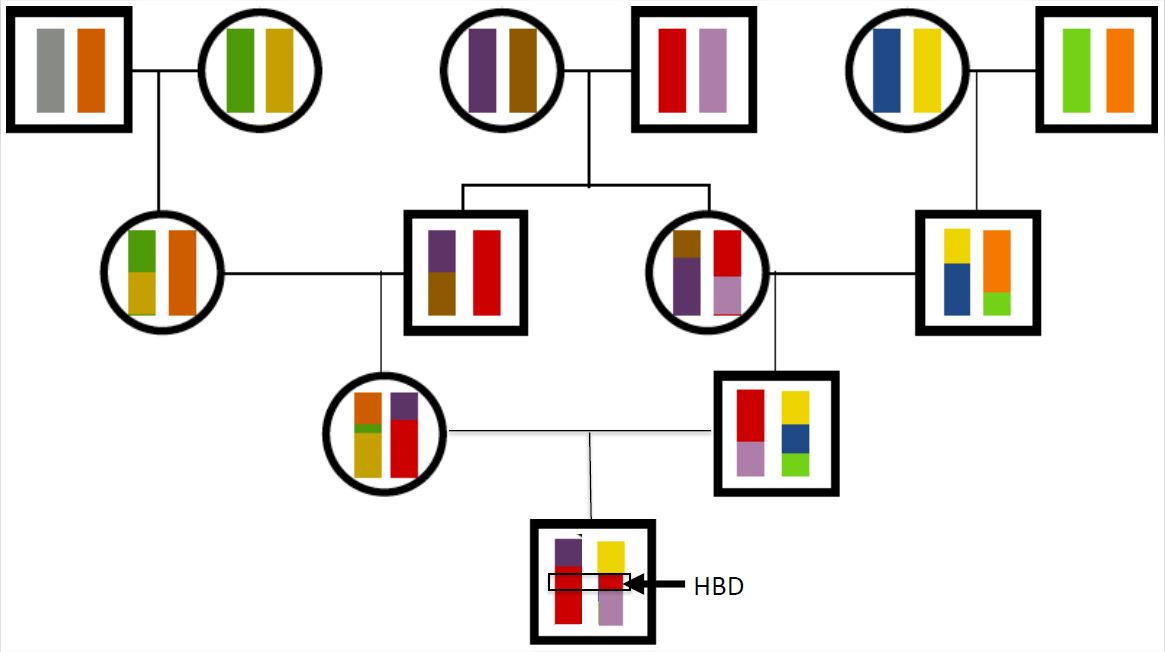
    Множинні петлі інбридингу збільшують ймовірність того, що дитина гомозиготна за спуском на локусі, який можна обчислити\(F\), просто включивши коефіцієнт інбридингу дитини в наше узагальнене рівняння HW.

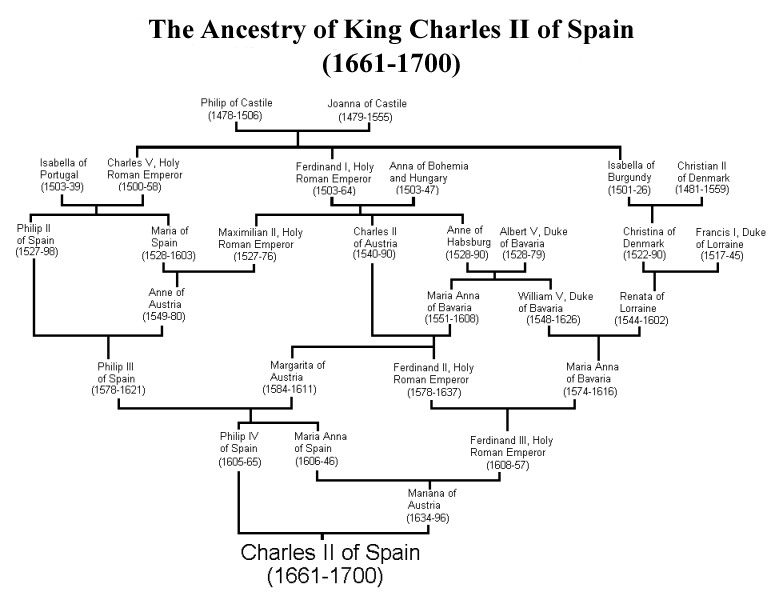
    Як один з крайніх прикладів впливу множинних петель інбридингу на родовід людини, давайте розглянемо короля Іспанії Карла II, останнього з іспанських Габсбургів. Карл був сином Філіпа IV Іспанського і Маріани Австрійської, які були дядьком і племінницею. Якби це була єдина петля інбридингу, то у Чарльза був би коефіцієнт інбридингу\(\frac{1}{8}\). На жаль для Чарльза, іспанські Габсбурги довго зберігали багатство і владу в своїй родині, влаштовуючи шлюби між близькими родичами. Родовід Карла II показана на малюнку\ ref {Fig:Carlos_second_pedigree}, і множинні петлі інбридингу очевидні. Наприклад, Філіп III, дід і прадід Карла II, сам був дитиною шлюбу дядька-племінниці.

    підрахував, що Карл II мав коефіцієнт інбридингу\(0.254\), еквівалентний повній в'язці, завдяки всім петлям інбридингу в його родоводу. Тому, як очікується, він був гомозиготним за походженням протягом повної чверті свого геному. Як ми поговоримо пізніше в цих примітках, це означає, що Чарльз, можливо, був гомозиготним для ряду алелів рецесивних захворювань, і справді він був дуже хворим чоловіком, який не залишив нащадків через своє безпліддя. Таким чином, правдоподібно кінець однієї з великих європейських династій відбувся через інбридинг.

    Розрахунок коефіцієнтів інбридингу за генетичними даними

    Якщо спостережувана гетерозиготність у популяції є\(H_O\), і ми припустимо, що узагальнені пропорції Харді — Вайнберга дотримуються, ми можемо встановити\(H_O\) рівну і розв'язати Equation\ ref {eq:HetgenHW} для\(F\) отримання оцінки\(f_{12}\) коефіцієнт інбридингу як

    \[\hat{F} = 1-\frac{f_{12}}{2pq} = \frac{2pq - f_{12}}{2pq}. \label{eqn:Fhat}\]

    Як і раніше,\(p\) це частота алелів\(A_{1}\) у популяції. Це може бути переписано з точки зору спостережуваної\(H_O\) гетерозиготності () і гетерозиготності, очікуваної при відсутності інбридингу\(H_E=2pq\), як

    \[\hat{F} = \frac{H_E-H_O}{H_E} = 1 - \frac{H_O}{H_E}. \label{eqn:FhatHO}\]

    Звідси\(\hat{F}\) кількісно оцінюється відхилення внаслідок інбридингу спостережуваної гетерозиготності від очікуваної при випадковому спарюванні, щодо останнього.

    Вправа\(\PageIndex{10}\)

    Припустимо, для локусу естерази спостерігалися наступні частоти генотипу в популяції дрозофіл (А позначає «швидкий» алель, а В позначає «повільний» алель):

    АА АБ ББ
    0.6 0.2 0.2

    Яка оцінка коефіцієнта інбридингу в локусі естерази?

    Якщо у нас кілька локусів, ми можемо замінити\(H_O\) і\(H_E\) за їх допомогою над локусами,\(\bar{H}_O\) і\(\bar{H}_E\), відповідно. Зверніть увагу, що, в принципі, ми також могли б спочатку обчислити\(F\) для кожного окремого локуса, а потім взяти середнє по локусах. Однак ця процедура більш схильна до введення зміщення, якщо розміри вибірки варіюються в різних локусах, що не малоймовірно, коли ми маємо справу з реальними даними.

    Генетичні маркери зазвичай використовуються для оцінки інбридингу диких та/або неволі популяцій, що викликають занепокоєння. Як приклад цього розглянемо випадок мексиканського вовка (Canis lupus baileyi), підвиду сірого вовка.

    5988399184_0c36a8e51c_z.jpg
    Малюнок\(\PageIndex{1}\): Сірий вовк (Canis lupus). \ BHLNC {Собаки, шакали, вовки
    та лисиці: монографія Canidae. 1890. y J.G. Keulemans} {https://www.biodiversitylibrary.org/...up}{University Торонто - Науково-інформаційний центр Герштейна}

    Вони були вилучені в дикій природі протягом середини 1900-х років через полювання, а решта п'ять мексиканських вовків у дикій природі були захоплені, щоб розпочати програму розмноження. оцінював поточну добу, середня очікувана гетерозиготність буде\(0.18\), заснована на частотах алелів на більш ніж сорока тисяч SNP. Однак середня особина мексиканського вовка спостерігалася лише гетерозиготною при\(12\%\) цих SNP. Тому середній коефіцієнт інбридингу для мексиканського вовка є\(\hat{F} = 1 -\frac{0.12}{0.18}\), тобто\(\sim 33 \%\) геном лобо гомозиготний через недавній інбридинг у своєму родоводу.

    Геномні блоки гомозиготності, обумовлені інбридингом.

    Як ми бачили вище, очікується, що близькі родичі поділять алелі IBD у великих геномних блоках. Таким чином, коли споріднених особин спаровуються і передають алелі інбредному потомству, вони передають ці алелі великими блоками через мейоз. Як приклад, повернемося до випадку наших гіпотетичних перших двоюрідних братів з малюнка\ ref {Fig:IBD_Cousins_chr_cartoon}. Якщо ця пара особин мала дитину, одна можлива картина генетичної передачі показана на малюнку\ ref {fig:kid_first_cousins}. Дитина успадкувала червону ділянку хромосоми двома різними шляхами через їхню родовід від бабусь і дідусів. Це приклад аутозиготного сегмента, де дитина гомозиготна по спуску на всіх локусах в цій червоній області.

    clipboard_e9e7c6ca2de6d6460d958a1ee56444834.png
    Малюнок\(\PageIndex{1}\): Родовід, що показує потомство перших двоюрідних братів. Хромосоми їхніх прабабусь і дідусів пофарбовані в різні кольори, тому їх передачу можна відстежувати. Дитина гомозиготна за походженням (HBD) для ділянки червоної хромосоми.

    Коефіцієнт інбридингу дитини встановлює частку їх генома, який буде перебувати в цих аутозиготних сегментах. Наприклад, дитина перших повних двоюрідних братів, як очікується,\(1/16\) матиме свій геном у цих сегментах. Чим віддаленіша петля в родоводу, тим більше мейозів, через які пройшли хромосом і тим коротше будуть окремі блоки. Дитина перших двоюрідних братів матиме довші блоки, ніж дитина другого двоюрідного брата, наприклад.

    Особи з множинними петлями інбридингу в своєму генеалогічному древі можуть мати високий коефіцієнт інбридингу через комбінованого ефекту багатьох дрібних блоків аутозиготності. Наприклад, Карл II мав коефіцієнт інбридингу, еквівалентний коефіцієнту дитини повних сибів, причому чверть його геному, як очікується, гомозиготна за походженням, але це складалося б з багатьох коротших блоків.

    Ми можемо сподіватися виявити ці блоки, шукаючи незвично довгі геномні пробіги ділянок гомозиготності (ROH) в геномі людини. Одним із способів оцінки коефіцієнта інбридингу індивіда є загальна частка генома людини, яка потрапляє в такі регіони ROH. Такий кошторис називається\(F_{ROH}\).

    Приклад використання\(F_{ROH}\) для вивчення інбридингу походить від роботи, який визначив гомозиготність у 2500 собак, починаючи від 500kb до багатьох мегабаз.

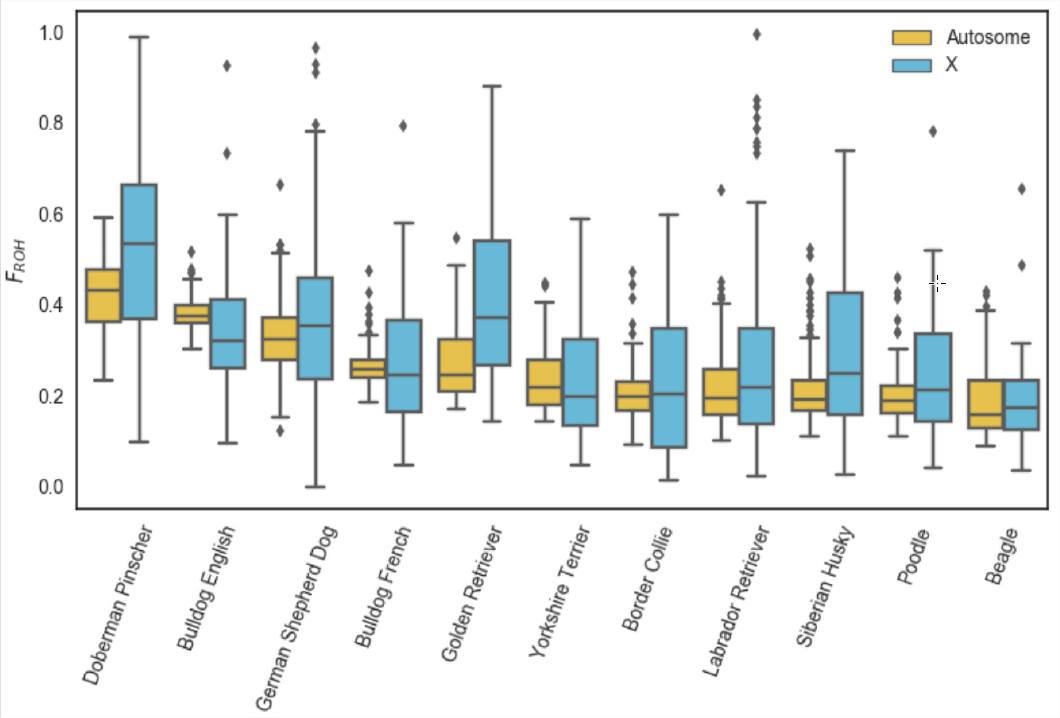
    clipboard_e23e438351361ea2b2f6788399c30e46f.png
    Малюнок\(\PageIndex{1}\):\(F_{ROH}\) Поширення особин з різних порід собак від,.

    Рисунок\ ref {Fig:dog_foh} показує розподіл особин у кожній породі собак для Х і аутосоми.\(F_{ROH}\) На малюнку\ ref {Fig:dog_foh_dist} це розбито на довжину сегментів ROH.

    14752595581_4330377c97_z.jpg
    Малюнок\(\PageIndex{1}\): Сукупна щільність довжини ROH, вимірюється в мегабазах (Мб) з для різних порід собак (). Зверніть увагу, що більші довжини ROH знаходяться зліва від ділянки.
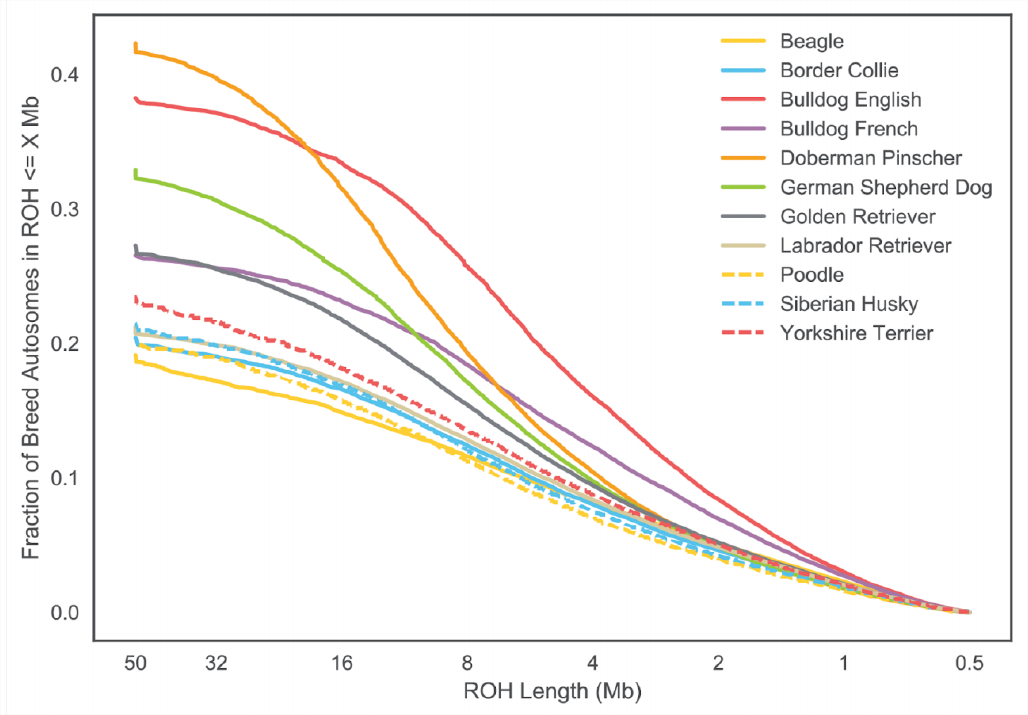
    clipboard_ebe150f191de0b496a9cd518f361b7610.png
    Малюнок\(\PageIndex{1}\): Сукупна щільність довжини ROH, вимірювана в мегабазах (Mb) від\ citet {Sams:18} для різних порід
    собак (\ plosCCby). Зверніть увагу, що більші довжини ROH знаходяться зліва від ділянки.

    Породи собак піддавалися інтенсивному розведенню, що призвело до високого рівня інбридингу. З досліджених популяційних зразків пінчери добермана мають найвищий рівень свого генома в гомозигозності (\(F_{ROH}\)), дещо вищий, ніж англійські бульдоги. У\ ref {Fig:dog_foh_dist} ми бачимо, що англійські бульдоги мають більш короткий ROH, ніж доберман-пінчери, але що доберман-пінчери мають більше свого генома в дуже великих ROH (\(>16 Mb\)). Це говорить про те, що англійські бульдоги мали довгу історію інбридингу, оскільки вони мають багато невеликих блоків, але що пінчери добермана мають багато недавніх інбридингів, оскільки їх аутозиготність міститься в довгих блоках відносно непорушених рекомбінацією.

    Резюме

    • Цей розділ розробив взаємозв'язок між частотами алелів та частотами генотипу всередині покоління та серед родичів.
    • Під випадковим спаровуванням ми вивели очікування частот генотипу (Харді-Вайнберг), і ми можемо виявити відхилення від цих очікувань.
    • Ідентичність за походженням (IBD) стосується спільного використання алелів через недавні спільні біологічні стосунки.
    • Можна прогнозувати ймовірність та очікуваний рівень поділу алелів IBD між парами родичів за допомогою менделінових ймовірностей передачі (як містяться в коефіцієнтах\(r_0\)\(r_1\), і\(r_2\)). Одним з корисних підсумків спорідненості для пари індивідів є коефіцієнт спорідненості\(F_{i,j}\).
    • Ми також можемо дізнатися про генетичні зв'язки від спільного використання геномних сегментів між родичами, причому багато довгих спільних сегментів виявляють тісніші стосунки.
    • Інбредна особа має батьків, які більш тісно пов'язані, ніж випадкові малюнки з якоїсь референтної популяції.
    • Інбридинг призводить до зниження гетерозиготності та комплементарного збільшення гомозиготності. Ми можемо використовувати коефіцієнт спорідненості батьків для оцінки спотворень від Харді-Вайнберга та очікуваного рівня гетерозиготності.
    • Коефіцієнти інбридингу можуть бути розраховані на основі генетичних даних, як для декількох особин в одному локусі, так і для декількох локусів для однієї особини.
    Вправа\(\PageIndex{11}\)

    Обчисліть\(r_{0}\)\(r_{1}\),\(r_{2}\) і коефіцієнт спорідненості\(F\) між:

    1. Бабуся і дідусь і їхній онук
    2. Прабабуся і дідусь і їх правнук
    3. Повні брати і сестри
    4. Велика тітка і її грандіозний племінник (ваша велика тітка = тітка вашого батька)
    Вправа\(\PageIndex{12}\)

    Ви вивчаєте співдомінантний квітковий поліморфізм. Пропускаючи через луг квітів ви і складаєте такі дані:

    червоний рожевий білий
    200 100 200
    1. Які частоти ви очікували б у цьому місці під рівновагою Харді-Вайнберга?
    2. Обчисліть коефіцієнт інбридингу в цьому місці.
    3. Назвіть два різних процеси, які можуть призвести до відхилення, яке ви бачите, і опишіть, як вони призведуть до дефіциту гетерозигот.
    Вправа\(\PageIndex{13}\)

    Які коефіцієнти спорідненості Х-хромосоми між:

    1. Двоє повних братів і сестер?
    2. Дві жінки повні брати і сестри?
    3. Яка ймовірність того, що жіноче потомство повної сіб-спаровування гомозиготно по спуску в локусі на її Х-хромосомі?
    Вправа\(\PageIndex{14}\)

    Ви вивчаєте поліморфізм плям крила у виду метеликів. З хрестів в лабораторії ви виявите, що наявність плям крила визначається домінуючим алелем.

    Ви збираєте 100 метеликів, 84 з них мають плями крила. Яка частота алелю крилової плями? Яке припущення ви повинні були зробити, щоб прийти до вашої відповіді?

    Вправа\(\PageIndex{15}\)

    Алель має частоту\(0.001\) в популяції. Яка ймовірність того, що і ви, і ваш перший (повний) двоюрідний брат є гетерозиготою для алеля?

    Вправа\(\PageIndex{16}\)

    Коефіцієнт спорідненості батьків - коефіцієнт інбридингу потомства. Поясніть, посилаючись на зважування коефіцієнтів спорідненості в коефіцієнті інбридингу, чому коефіцієнт інбридингу - це ймовірність того, що локус гомозиготний за зниженням.

    Вправа\(\PageIndex{17}\)

    Що стосується ідентичності за походженням, поясніть, чому багаторазові петлі інбридингу в родоводу людини призводять до більш високого рівня інбридингу.