Skip to main content
LibreTexts - Ukrayinska

5: Ймовірність

  1. Last updated
  2. Save as PDF
  • Page ID
    29768

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ми розглядали модель системи обробки інформації, в якій символи з входу кодуються в біти, які потім надсилаються через «канал» до приймача і декодуються назад в символи. Див. Малюнок 5.1.

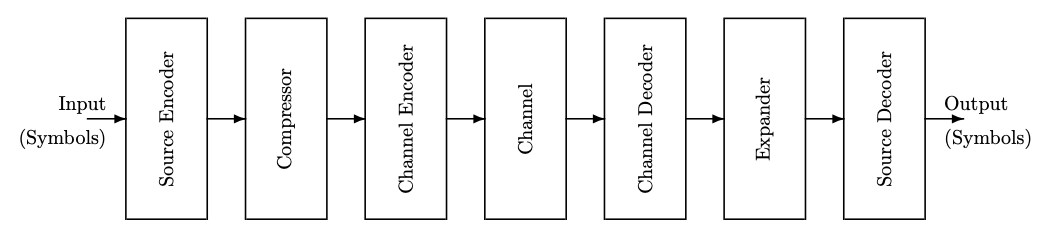
    Знімок екрана 2021-05-02 в 1.17.33 PM.png
    Малюнок 5.1: Система зв'язку

    У попередніх розділах цих заміток ми розглядали різні компоненти цієї моделі. Тепер повернемося до джерела і моделюємо його більш повно, з точки зору розподілу ймовірностей.

    Джерело надає символ або послідовність символів, вибраних з деякого набору. Процес вибору може бути експериментом, таким як гортання монети або прокатки кубиків. Або це може бути спостереження за діями, не викликаними спостерігачем. Або послідовність символів може бути з представлення якогось об'єкта, наприклад символів з тексту або пікселів із зображення.

    Ми розглядаємо лише випадки з кінцевою кількістю символів на вибір, і лише випадки, коли символи є як взаємовиключними (одночасно можна вибрати лише один), так і вичерпними (один фактично обраний). Кожен вибір є «результатом», і наша мета полягає в тому, щоб простежити послідовність результатів та інформацію, яка їх супроводжує, коли інформація рухається від входу до виходу. Для цього нам потрібно вміти сказати, який результат, а також наші знання про деякі властивості результату.

    Якщо ми знаємо результат, у нас є абсолютно хороший спосіб позначення результату. Ми можемо просто назвати обраний символ, і ігнорувати всі інші символи, які не були обрані. Але що робити, якщо ми ще не знаємо результату, або в якійсь мірі невпевнені? Як ми повинні виражати свій стан знань, якщо є невизначеність? Ми будемо використовувати для цього математику ймовірності.

    Щоб проілюструвати цю важливу ідею, ми будемо використовувати приклади, засновані на характеристиках студентів MIT. Офіційний підрахунок студентів MIT\(^1\) за осінь 2007 включає дані в таблиці 5.1, яка відтворюється у форматі діаграми Венна на малюнку 5.2.

    Жінкам Чоловіки Всього
    Першокурсники 496 577 1 073
    Магістранти 1 857 2 315 4 172
    Аспіранти 1 822 4 226 6 048
    Всього студентів 3 679 6 541 10 220
    Таблиця 5.1: Демографічні дані для MIT, осінь 2007
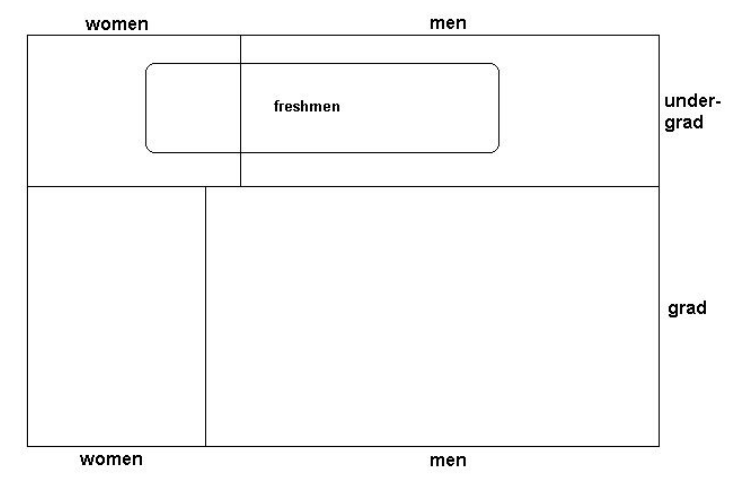
    Знімок екрана 2021-05-02 о 1.20.48 PM.png
    Малюнок 5.2: Діаграма Венна даних студентів MIT з областями, які повинні бути пропорційні розмірам субпопуляцій.

    Припустимо, що обраний першокурсник MIT (обраний символ - це індивідуальний студент, а набір можливих символів - 1073 першокурсники), і вам не повідомляють, хто це. Вам цікаво, жінка це чи чоловік. Звичайно, якби ви знали особистість обраного студента, ви б знали стать. Але якщо ні, то як ви могли б охарактеризувати свої знання? Яка ймовірність, або ймовірність того, що жінка була обрана?

    Відзначимо, що 46% від класу першокурсників 2007 року (496/1073) складають жінки. Це факт, або статистика, яка може представляти, а може і не представляти ймовірність того, що першокурсник обрав жінку. Якщо у вас були підстави вважати, що всі першокурсники однаково ймовірно будуть обрані, ви можете вирішити, що ймовірність того, що це жінка становить 46%. Але що робити, якщо вам скажуть, що відбір проводиться в коридорі McCormick Hall (жіночий гуртожиток)? У такому випадку ймовірність того, що першокурсник обрав жінку, ймовірно, вище 46%. Статистику і ймовірності можна описати, використовуючи одну і ту ж математику (буде розроблена далі), але це різні речі.

    \(^1\)всі студенти: http://web.mit.edu/registrar/www/sta...portfinal.html, всі жінки: http://web.mit.edu/registrar/www/sta...omenfinal.html