11.7: Проблеми

11.1. У наведених нижче прикладах визначте, чи$f$ є функція чи функціонал.

• А парабола описується$f(x) = x^2$.
• З огляду на дві форми енергії і шлях$y(t)$,$f$ є Лагранж системи$\mathcal{L} \left( t, y, \frac{dy}{dt} \right)$.
• Враховуючи величину швидкості$|\overrightarrow{v}(t)|$ об'єкта,$f$ представляє відстань, яку об'єкт проходить від часу 0 до часу 3600 секунд.
• Враховуючи положення$(x, y, z)$ в просторі,$f(x, y, z)$ представляє відстань від цієї точки до початку.

11.2. А система має Лагранж$\mathcal{L} \left( t, y, \frac{dy}{dt} \right) = \left(\frac{dy}{dt}\right)^3 + e^{3y}$. Знайдіть рівняння для шляху$y(t)$, яке мінімізує дію$\int_{t_{1}}^{t_{2}} \mathcal{L}\left(t, y, \frac{d y}{d t}\right) d t$. (Результат нелінійний, тому не намагайтеся його вирішити.)

11.3. Система має Лагранж$\mathcal{L} \left( t, y, \frac{dy}{dt} \right) = \frac{1}{2}\left(\frac{dy}{dt}\right)^2 + \frac{1}{2} \cdot y^{-2}$. Знайдіть відповідне рівняння руху. (Результат нелінійний, тому не намагайтеся його вирішити.)

11.4. Малюнок 11.4.2 ілюструє три можливі шляхи для системи масових пружин та відповідні їм дії. Розглянуті шляхи:

$$x_{1}(t) = 2 t-1\nonumber$$

$$x_{2}(t) = 2 t^2-1\nonumber$$

$$x_{3}(t) =-\cos (\pi t)\nonumber$$

Для кожного шляху обчисліть дію за допомогою Рівняння 11.4.10 для перевірки значень, показаних на малюнку. Припустимо, що маса$m$ = 1 кг і постійна пружина$K = \pi^2 \frac{J}{m^2}$.

11.5. На малюнку зображена пружина кручення. Він може зберігати потенційну енергію$\frac{1}{2} \mathbb{K} \theta^{2}$, і він може перетворювати потенційну енергію в кінетичну енергію$\frac{1}{2} \mathbb{I}\left(\frac{d \theta}{d t}\right)^{2}$. У цих виразах$\theta(t)$ - це величина кута повороту пружини в радіанах, і$\omega=\frac{d \theta}{d t}$ це величина кутової швидкості в радіанах в секунду. $\mathbb{K}$є постійною пружини кручення, і$I$ є (постійним) моментом інерції.

(а) Знайдіть Лагранжа.

(b) Використовуйте рівняння Ейлера-Лагранжа, щоб знайти диференціальне рівняння, що описує$\theta(t)$.

(c) Покажіть, що енергія зберігається в цій системі, показавши це$\frac{dH}{dt} = 0$.

(d) Налаштуйте рівняння Гамільтона.

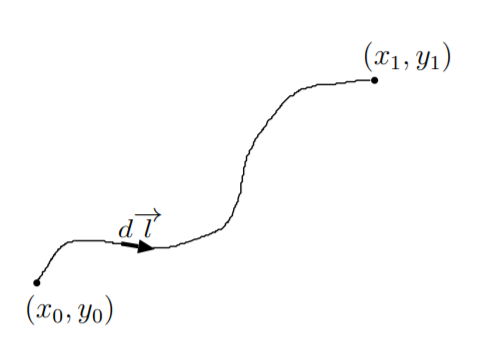
11.6. Мета цієї проблеми полягає в тому, щоб вивести найкоротший шлях$y(x)$ між точками$(x_0, y_0)$ і$(x_1, y_1)$. Розглянемо довільний шлях між цими точками, як показано на малюнку. Ми можемо розбити шлях на диференціальні елементи$d\overrightarrow{l}=d x \hat{a}_{x}+d y \hat{a}_{y}$. Величина кожного диференціального елемента дорівнює

$$|d \overrightarrow{l}|=\sqrt{(d x)^{2}+(d y)^{2}}=d x \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}.\nonumber$$

Відстань між точками можна описати дією

$$\mathbb{S}=\int_{x_{0}}^{x_{1}} \sqrt{1+\left(\frac{d y}{d x}\right)^{2}} d x.\nonumber$$

Щоб знайти шлях,$y(x)$ який мінімізує дію, ми можемо вирішити рівняння Ейлера-Лагранжа, з$\mathcal{L}=\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}$ як Лагранжа, для цього найкоротшого шляху$y(x)$. Цей підхід може бути використаний, оскільки ми хочемо мінімізувати інтеграл деякого функціоналу,$\mathcal{L}$ хоча цей функціонал не представляє різниці енергії [163, с. 33].

Налаштуйте рівняння Ейлера-Лагранжа та вирішіть його для найкоротшого шляху$y(x)$.

Підказка 1: Відповідь на цю проблему полягає в тому, що найкоротший шлях між двома точками - пряма лінія. Тут ви виведете цей результат.

Підказка 2: У прикладах цієї глави Лагранж мав форму$\mathcal{L} \left( t, y, \frac{dy}{dt} \right)$ з незалежною змінною$t$ та шляхом$y(t)$. Тут Лагранж має вигляд,$\mathcal{L} \left( x, y, \frac{dy}{dx} \right)$ де незалежна змінна -$x$ position, а шлях -$y(x)$.

Підказка 3: Якщо$\frac{d} {dx} (something) = 0$, то ви знаєте, що$(something)$ є постійною.

11.7. Світло рухається по найшвидшому шляху між двома точками. Ця ідея відома як принцип Ферма. У матеріалі з відносною діелектричною проникністю$\epsilon_r$ і проникністю світло$c$ рухається з постійною швидкістю$\mu_0$,$\frac{c}{\sqrt{\epsilon_{r}}}$ де швидкість світла у вільному просторі. У проб. 11.6 ми показали, що найкоротший шлях між двома точками - пряма, тому в однорідному матеріалі світло буде проходити по прямій лінії між двома точками. Однак що робити, якщо світло рухається через стик між двома матеріалами? У цій проблемі ми відповімо на це питання і виведемо відомий результат, відомий як закон Снелла.

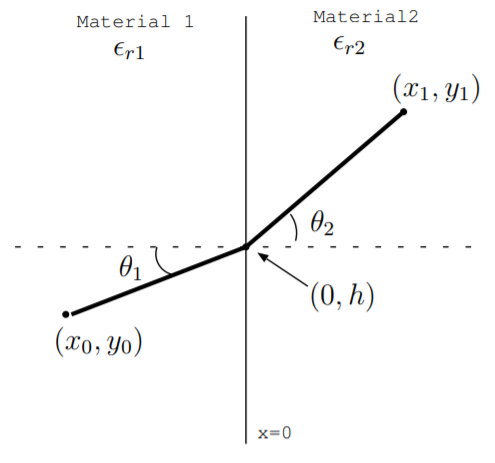
Розглянемо малюнок нижче. Припустимо, що промінь світла рухається від$(x_0, y_0)$ до$(x_1, y_1)$ уздовж шляху, який займає найкоротший час. Матеріал 1 має відносну діелектричну проникність$\epsilon_{r1}$, тому світло рухається в цьому матеріалі з постійною швидкістю$\frac{c}{\sqrt{\epsilon_{r1}}}$. Матеріал 2 має відносну діелектричну проникність$\epsilon_{r2}$, тому світло рухається в цьому матеріалі з постійною швидкістю$\frac{c}{\sqrt{\epsilon_{r2}}}$. Як ми вивели в Prob. 11.6, світло рухається по прямій лінії в матеріалі 1, і він рухається по прямій лінії в матеріалі 2. Однак лінії мають різні нахили, як показано на малюнку. Припустимо, що стик двох матеріалів відбувається за адресою$x = 0$.

(а) Знайдіть рівняння для загального часу, який займає світло для подорожі як функція вертикальної відстані$h$, на якій шлях перетинає$y$ вісь. Зверніть увагу, що ви знаходите тут функцію$F(h)$, а не функціонал. Ви можете використовувати той факт, що ви знаєте, що світло слідує прямій лінії всередині кожного матеріалу, щоб знайти цю функцію.

(б) Шляхи, за якими слідує світло, займає мінімальний час, тому похідна$\frac{dF}{dh} = 0$. Скористайтеся цією ідеєю, щоб знайти рівняння для невідомої висоти вертикалі$h$. Ваша відповідь може бути записана як функція відомих констант$\epsilon_{r1}$,$\epsilon_{r2}$$x_0$,$y_0$,$x_1$,$y_1$, і$c$. Вам не потрібно вирішувати для$h$ тут, а замість цього просто оцінити похідну і встановити її на нуль.

(c) Використовуйте свій результат у частині b вище, щоб вивести закон Снелла:

$$\sqrt{\epsilon_{r 1}} \sin \theta_{1}=\sqrt{\epsilon_{r 2}} \sin \theta_{2}.\nonumber$$

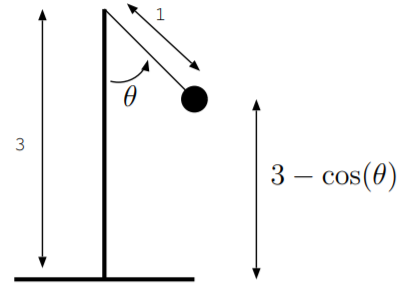
11.8. Маятник перетворює кінетичну енергію в та від гравітаційної потенційної енергії. Як показано на малюнку, куля масою m підвішується струною довжиною 1 м. Маятник монтується на підставу висотою 3 м. Як показано на малюнку,$\theta(t)$ це кут маятника. Кінетична енергія кулі задається$E_{kinetic} = \frac{1}{2}m \left(\frac{d\theta}{dt}\right)^2$, а гравітаційна потенційна енергія задається$E_{p.e.} = mg (3 − \cos \theta)$. Величина$g$ - гравітаційна константа,$g = 9.8 \frac{m}{s^2}$.

(а) Знайти$\mathcal{L}$, Лагранж системи.

(б) Знайти$H$, гамільтоніан системи.

(c) Встановіть рівняння Ейлера-Лагранжа і використовуйте його$\theta(t)$, щоб знайти рівняння руху для кута маятника як функція часу.

(d) Показати, що енергія зберігається в цій системі, показуючи це$\frac{dH}{dt} = 0$.

Рівняння руху, знайдене в частині c, є нелінійним, тому не намагайтеся його вирішити. Цікаво, що він має закриту форму розчину [164, гл. 6]. (Ця проблема є модифікованою версією прикладу у посиланні [163].)

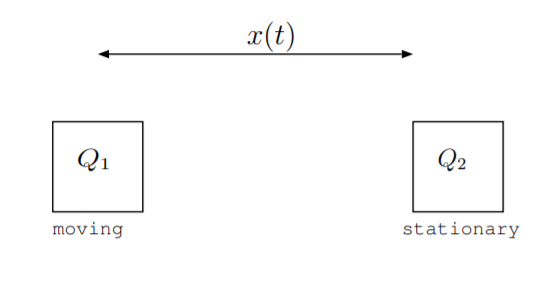
11.9. Як показано на малюнку, об'єкт заряду$Q_1$ і маси$m$ рухається поблизу нерухомого об'єкта з зарядом$Q_2$. Припустимо, що маса і заряди є константами, і припустимо, що об'єкти оточені вільним простором. Кінетична енергія рухомого об'єкта перетворюється в енергію, що зберігається в електричному полі між об'єктами або з неї. Кінетична енергія рухомого об'єкта задається за допомогою$\frac{1}{2}m\left(\frac{dx}{dt}\right)^2$. Енергія електричного поля задається тим,$\frac{Q_1Q_2}{4\pi\epsilon_0x}$ де$\epsilon_0$ діелектрична проникність вільного простору. Відстань між об'єктами задається за допомогою$x(t)$.

(а) Знайдіть Лагранжа системи.

(б) Знайти узагальнений імпульс.

(c) Знайти узагальнений потенціал.

(г) Знайти рівняння руху для шляху$x(t)$ системи. (Не намагайтеся вирішити це нелінійне рівняння.)

(е) Знайти загальну енергію системи.

(f) Показати, що енергія зберігається в цій системі.