11.5: Приклад індуктора конденсатора
- Page ID
- 29446
Ідеї обчислення варіацій стосуються і процесів перетворення енергії в електричних системах. Розглянемо схему з конденсатором і індуктором, як показано на малюнку\(\PageIndex{1}\). Струм\(i_L\), струм\(i_c\), напруга\(v\) визначаються на малюнку. Припустимо, що дроти і комплектуючі не мають опору. Хоча це не зовсім фізично, це дозволить нам спростити проблему. Припустимо, що конденсатор заряджений для\(t < 0\), а вимикач відкритий. При\(t = 0\), вимикач замкнутий, і конденсатор починає розряджатися. В даному прикладі узагальненим шляхом буде заряд, накопичений на обкладинках конденсатора. Ми можемо вивести рівняння руху, яке описує цей шлях.
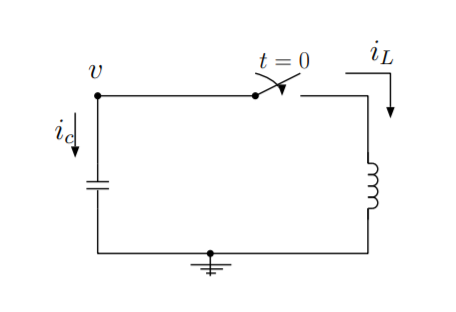
Енергія перетворюється між двома формами. Перша форма енергії в цій системі - це електрична енергія, що зберігається в конденсаторі. Напруга\(v\) в вольтах на конденсаторі пропорційна заряду\(Q\) в кулоні на обкладинках конденсатора. Ємність\(C\), виміряна в фарадах, є постійною пропорційності між двома заходами.
\[Q = Cv \nonumber \]
Співвідношення струм-напруга на конденсаторі можна знайти, взявши похідну по відношенню до часу.
\[\frac{dQ}{dt} = C\frac{dv}{dt} \label{11.5.2} \]
Зміна заряду нарощування по відношенню до часу - це струм. Більш конкретно,
\[\frac{dQ}{dt} = i_c = -i_L. \label{11.5.3} \]
Рівняння\ ref {11.5.2} і\ ref {11.5.3} можуть бути об'єднані.
\[-i_L = C\frac{dv}{dt}. \nonumber \]
Енергія, що зберігається в конденсаторі
\[E_{c a p}=\frac{1}{2} C v^{2}. \nonumber \]
Друга форма енергії в цій системі - енергія, що зберігається в магнітному полі індуктора. Струм\(i_L\) через індуктор, вимірюваний в амперах, пропорційний магнітному потоку\(\Psi\), вимірюваному в Веберах, навколо індуктора. Індуктивність\(L\), виміряна в Генрі, є постійною пропорційності між струмом і магнітним потоком.
\[\Psi = Li_L \nonumber \]
Співвідношення напруги струму на цьому індукторі можна знайти, взявши похідну щодо часу.
\[\frac{d \Psi}{d t}=v=L \frac{d i_{L}}{d t} \nonumber \]
Енергія, що зберігається в індукторі, задається
\[E_{ind}=\frac{1}{2} L i_{L}^{2} \nonumber \]
Ми описуємо процес перетворення енергії шляхом відстеження узагальненого шляху\(Q(t)\), заряду, що зберігається на конденсаторі. Змінна\(t\) представляє незалежну змінну час у секундах і\(Q\) є залежною змінною заряд в кулоні. Гамільтонова і Лагранжева,\(H\) і\(L\), будуть розглянуті функції трьох незалежних змінних:\(t\),\(Q\), і\(\frac{dQ}{dt}\).
Гамільтоніан - це сума енергії в конденсаторі і енергії в індукторі. Лагранж - це різниця між цими енергіями.
\[H = E_{total} = E_{cap} + E_{ind} \nonumber \]
\[\mathcal{L} = E_{cap} - E_{ind} \nonumber \]
Інженери-електрики зазвичай описують фізичні схеми, використовуючи найбільш легко вимірювані величини: струм і напруга. Однак тут, щоб проілюструвати використання числення варіаційного формалізму, ми пишемо вирази як для загальної енергії, так і для Лагранжа в терміні заданих змінних:\(t\),\(Q\), і\(\frac{dQ}{dt}\).
\[H\left(t, Q, \frac{d Q}{d t}\right)=\frac{1}{2 C} Q^{2}+\frac{1}{2} L\left(\frac{d Q}{d t}\right)^{2} \nonumber \]
\[\mathcal{L}\left(t, Q, \frac{d Q}{d t}\right)=\frac{1}{2 C} Q^{2}-\frac{1}{2} L\left(\frac{d Q}{d t}\right)^{2} \nonumber \]
Ми можемо знайти шлях, заряд на конденсаторі як функція часу, вирішивши для найменшого дії
\[\delta\left|\int_{t_{1}}^{t_{2}} \mathcal{L}\left(t, x, \frac{d x}{d t}\right) d t\right|=0 \label{11.5.13} \]
або шляхом розв'язання рівняння Ейлера-Лагранжа,
\[\frac{\partial \mathcal{L}}{\partial Q}-\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial\left(\frac{d Q}{d t}\right)}=0. \label{11.5.14} \]
У Equation\ ref {11.5.13}\(\delta\) вказує першу варіацію, визначену рівнянням 11.3.5. Розчини залежать від початкових умов, таких як заряд, що зберігається в конденсаторі, і струм в індукторі в початковий час. Ми можемо використовувати рівняння Ейлера-Лагранжа, щоб знайти рівняння руху. Перший член Рівняння\ ref {11.5.14} є узагальненим потенціалом,
\[\frac{\partial \mathcal{L}}{\partial Q} = \frac{Q}{C} \nonumber \]
яка є напругою\(v\) в вольтах. Наступний член - похідна від узагальненого імпульсу.
\[\mathbb{M}=\frac{\partial \mathcal{L}}{\partial\left(\frac{d Q}{d t}\right)}=-L \frac{d Q}{d t} \nonumber \]
Ми можемо зібрати шматки разом, щоб знайти вираз збереження узагальненого потенціалу.
\[\frac{Q}{C}+L \frac{d^{2} Q}{d t^{2}}=0 \label{11.5.17} \]
Це твердження закону Кірхгофа про напругу. Виглядає більш звично, якщо написано в плані напруги\(v = \frac{Q}{C}\) і струму\(i_L = -\frac{dQ}{dt}\).
\[v-L \frac{d i_{L}}{d t}=0 \nonumber \]
Ми можемо вирішити рівняння руху, Equation\ ref {11.5.17}, використовуючи відповідні початкові умови, щоб знайти шлях. Як і в прикладі масової пружини, Equation\ ref {11.5.17} є хвильовим рівнянням, а його розв'язками є синусоїди. Як і очікувалося, схема, виготовлена лише з конденсатора та індуктора, є генератором.
| Пристрій накопичувача енергії | Конденсатор | Лінійна пружина |
|---|---|---|
| Узагальнений шлях | Зарядка\(Q\) в С | Водотоннажність\(\overrightarrow{x}\) в м |
| Узагальнений потенціал | Напруга\(v\) в\(\frac{J}{C} = V\) | \(\overrightarrow{F}\)Сила в\(\frac{J}{m} = N\) |
| Узагальнена ємність | Ємність\(C\) в F =\(\frac{C^2}{J}\) | \(\frac{1}{K}\)в\(\frac{m^2}{J}\) |
| Конститутивні відносини | \(Q=Cv\) | \(\overrightarrow{x} = \frac{1}{K}\overrightarrow{F}\) |
| Енергетика | \(\frac{1}{2}Cv^2\) | \(\frac{1}{2}\frac{1}{K}|\overrightarrow{x}|^2 = \frac{1}{2}K|\overrightarrow{F}|^2\) |
| Закон для потенціалу | КВЛ | Другий закон Ньютона\(\overrightarrow{F} = m\overrightarrow{a}\) |
Крім того, ми можемо показати, що енергія зберігається в цьому процесі перетворення енергії, оскільки часткова похідна як загальної енергії, так і Лагранжа щодо часу дорівнює нулю.
\[\frac{\partial \mathcal{L}}{\partial t}=\frac{\partial H}{\partial t}=0 \nonumber \]
\[\frac{d \mathcal{L}}{d t}=\frac{d H}{d t}=0 \nonumber \]
Таблиця\(\PageIndex{2}\) підсумовує цей приклад. Він також ілюструє взаємозв'язок між параметрами цього прикладу та параметрами прикладу пружини маси.
