10.8: Діаграма випромінювання

Діаграма випромінювання передавальної антени описує величину і поляризацію поля, випромінюваного антеною як функцію кута щодо антени. Шаблон також може бути визначена для приймальної антени, однак, ми відкладаємо обговорення випадку прийому на більш пізній розділ.

Поняття діаграми випромінювання тісно пов'язане з поняттями спрямованості і посилення (розділ 10.7). Головною відмінністю є явний розгляд поляризації. У багатьох додатках поляризація поля, випромінюваного передавальною антеною, так само важлива, як щільність потужності, що випромінюється антеною. Наприклад, канал радіозв'язку складається з антени, яка передається відокремлена деякою відстанню від антени, яка приймає. Спрямованість визначає щільність потужності, що доставляється до приймальної антени, але приймальна антена повинна бути спільно поляризована з прибуває хвилею, щоб захопити всю цю потужність.

Концепція радіаційної діаграми, мабуть, найкраще пояснюється на прикладі. Найпростіша антена зустрічається в звичайній практиці - це електрично-короткий диполь (ESD), який складається з прямого дроту довжиною$L$, яка набагато менше половини довжини хвилі. У розділі 9.5 показано, що поле, випромінюване ESD, яке розташоване біля початку та вирівняне вздовж$z$ осі -є:

$$\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \eta \frac{I_0\cdot\beta L}{8\pi} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} \label{m0205_eESDE}$$

де$I_0$ представляє величину і фазу струму, прикладеного до клем,$\eta$ - хвильовий опір середовища, і$\beta=2\pi/\lambda$ є постійною поширення фази середовища. Зверніть увагу, що орієнтовний напрямок електричного поля знаходиться в$\hat{\bf \theta}$ напрямку; отже, приймач повинен бути$\hat{\bf \theta}$ -поляризований відносно системи координат передавача, щоб захопити всю наявну потужність. Приймач, який не повністю$\hat{\bf \theta}$ поляризований, захопить менше енергії. В крайньому випадку приймач, який$\hat{\bf \phi}$ поляризований по відношенню до системи координат передавача буде захоплювати нульову потужність. Таким чином, для$\hat{\bf z}$ -орієнтованого ОУР ми називаємо$\hat{\bf \theta}$ -поляризацію переданого поля як «кополяризований» або просто «ко-пол», а$\hat{\bf \phi}$ -поляризацію переданого поля як «крос-пол».

У цей момент читач може задатися питанням, якій меті служить визначення перехресної поляризації, оскільки визначення, наведене вище, здається, припускає, що крос-пол завжди повинен бути нулем. У звичайній інженерній практиці крос-пол ненульовий, коли ко-пол відрізняється від передбачуваної або номінальної поляризації поля, випромінюваного антеною. У випадку з ОУР ми спостерігаємо, що електричне поле завжди$\hat{\bf \theta}$ -поляризоване, і тому вважаємо це номінальною поляризацією. Оскільки фактична поляризація ОУР в прикладі точно така ж, як і номінальна поляризація ОУР, крос-пол ідеального ОУР дорівнює нулю. Якщо, з іншого боку, ми довільно$\hat{\bf \theta}$ визначаємо номінальну поляризацію і застосувати це визначення до іншої антени, яка не виробляє рівномірно$\hat{\bf \theta}$ -поляризоване електричне поле, то ми спостерігаємо ненульовий крос-пол. Cross-pol аналогічно використовується для кількісної оцінки ефектів через помилки в положенні або орієнтації, або через небажану модифікацію поля через матеріали (наприклад, подача або монтажні конструкції) поблизу передавальної антени. Підводячи підсумки:

Co-POL зазвичай визначається як передбачувана або номінальна поляризація для конкретного застосування, що не обов'язково фактична поляризація, випромінювана розглянутою антеною. Крос-пол вимірює поляризацію в ортогональній площині; тобто відхилення від передбачуваного ко-пол.

Повернення до ESD: Оскільки$\widetilde{\bf E}({\bf r})$ залежить тільки від,$\theta$ а не$\phi$, шаблон co-pol однаковий у будь-якій площині, яка містить$z$ вісь. Ми маємо на увазі будь-яку таку площину, як E-plane. Загалом:

Е-площина - це будь-яка площина, в якій$\widetilde{\bf E}$ лежить номінальний або намічений вектор.

Оскільки ESD$\hat{\bf \theta}$ -поляризований, схема E-площини ESD просто:

$$\left|\widetilde{\bf E}({\bf r})\right| \approx \eta \frac{I_0\cdot\beta L}{8\pi} ~\left(\sin\theta\right) ~\frac{1}{r} \label{m0205_eEESD}$$

Ця форма показана на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$: E-plane co-pol шаблон для$\hat{\bf{z}}$ -орієнтованого ОУР. У ненормованому масштабуванні візерунка пунктирне коло вказує максимальне значення Equation\ ref {M0205_EEEESD}. (CC BY-SA 4.0; S. Lally)

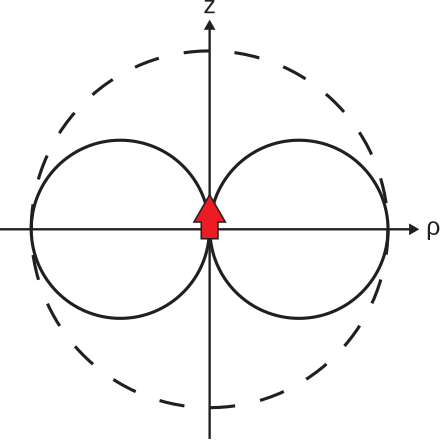
Рівняння\ ref {M0205_EEESD} називають ненормованим шаблоном. Пов'язаний нормалізований шаблон буде розглянуто пізніше в цьому розділі.

Аналогічно визначаємо H-площину наступним чином:

H-площина - це будь-яка площина, в якій$\widetilde{\bf H}$ лежить номінальний або призначений вектор, і так перпендикулярна як до E-площині, так і напрямку поширення.

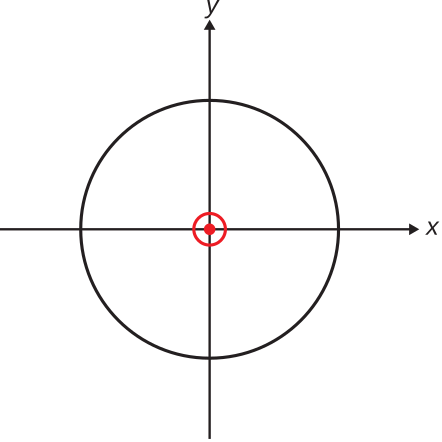
У випадку з ОУР єдиною H-площиною є$z=0$ площина. Візерунок H-площини показаний на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: H-площина co-pol шаблон для z-орієнтованого ОУР. У ненормованому масштабуванні візерунка радіус кола є максимальним значенням Equation\ ref {M0205_EEEESD}. (CC BY-SA 4.0; С.Лаллі)

Часто корисно нормалізувати візерунок, а це означає, що ми масштабуємо візерунок так, щоб його максимальна величина відповідала зручному значенню. Існує два загальних масштабування. Одне загальне масштабування встановлює максимальне значення шаблону, рівне 1, і тому не залежить від величини джерела та відстані. Це називається нормованим малюнком. Нормований шаблон co-pol можна визначити наступним чином:

$$F(\theta,\phi) \triangleq \frac{\left|\hat{\bf e}\cdot\widetilde{\bf E}({\bf r})\right|}{\left|\hat{\bf e}\cdot\widetilde{\bf E}({\bf r})\right|_{max}} \label{m0205_eNormPat}$$

де$\hat{\bf e}$ - орієнтир ко-поля, а знаменник - максимальне значення електричного поля на відстані$r$.

Нормований шаблон масштабується до максимальної величини 1, використовуючи визначення, виражене в Equation\ ref {M0205_enormpat}.

Зверніть увагу,$r$ що значення не має значення, так як чисельник і знаменник обидва масштабу з$r$ однаковим чином. Таким чином, нормована картина, як і спрямованість, не змінюється з відстанню від антени.

Для ОУР, таким чином$\hat{\bf e}=\hat{\bf \theta}$, нормалізована схема co-pol:

$$F(\theta,\phi) = \frac{\left|\hat{\bf \theta}\cdot\widetilde{\bf E}({\bf r})\right|}{\left|\hat{\bf \theta}\cdot\widetilde{\bf E}({\bf r})\right|_{max}} ~~~ \mbox{(ESD)} \nonumber$$

який дає просто

$$F(\theta,\phi) \approx \sin\theta ~~~ \mbox{(ESD)} \nonumber$$

Таким чином, нормована схема Е-площини ко-пол ОУР є Рисунок,$\PageIndex{1}$ де радіус кола максимального значення дорівнює 1, що дорівнює 0 дБ. Аналогічно, H-площина нормована спів-пол картини ESD є Рисунок,$\PageIndex{2}$ де радіус кола дорівнює 1 (0 дБ).

Інше поширене масштабування для візерунків встановлює максимальне значення, рівне максимальній спрямованості. Спрямованість пропорційна щільності потужності, яка пропорційна$\left|\widetilde{\bf E}({\bf r})\right|^2$. Тому ця картина «нормована спрямованість» може бути виражена у вигляді:

$$D_{max}\left|F(\theta,\phi)\right|^2 \nonumber$$

де$D_{max}$ - спрямованість в будь-якому напрямку вона максимальна. Для розглянутого раніше ОУР$D_{max}=1.5$ (Розділ 10.7). Таким чином, модель co-pol ОУР з використанням цього конкретного масштабування є

$$1.5 \sin^2\theta ~~~ \mbox{(ESD)} \nonumber$$

Таким чином, E-plane co-pol картина ОУР з використанням цього масштабування аналогічна малюнку$\PageIndex{1}$, за винятком того, що вона зведена в квадрат за величиною і радіус кола максимального значення дорівнює 1,5, що становить 1,76 дБ. H-площина co-pol шаблон ESD, використовуючи це масштабування, є Рисунок,$\PageIndex{2}$ де радіус кола дорівнює 1,5 (1.76 дБ).

Візерунок пелюсток

Майже всі антени загального користування демонструють спрямованість, яка більша, ніж у ESD. Шаблони цих антен згодом демонструють більш складну структуру. На$\PageIndex{3}$ малюнку наведено приклад.

Малюнок$\PageIndex{3}$: Co-pol шаблон типовий для високо спрямованої антени, наприклад, яги. (CC BY-SA 4.0 (модифікований); Т.

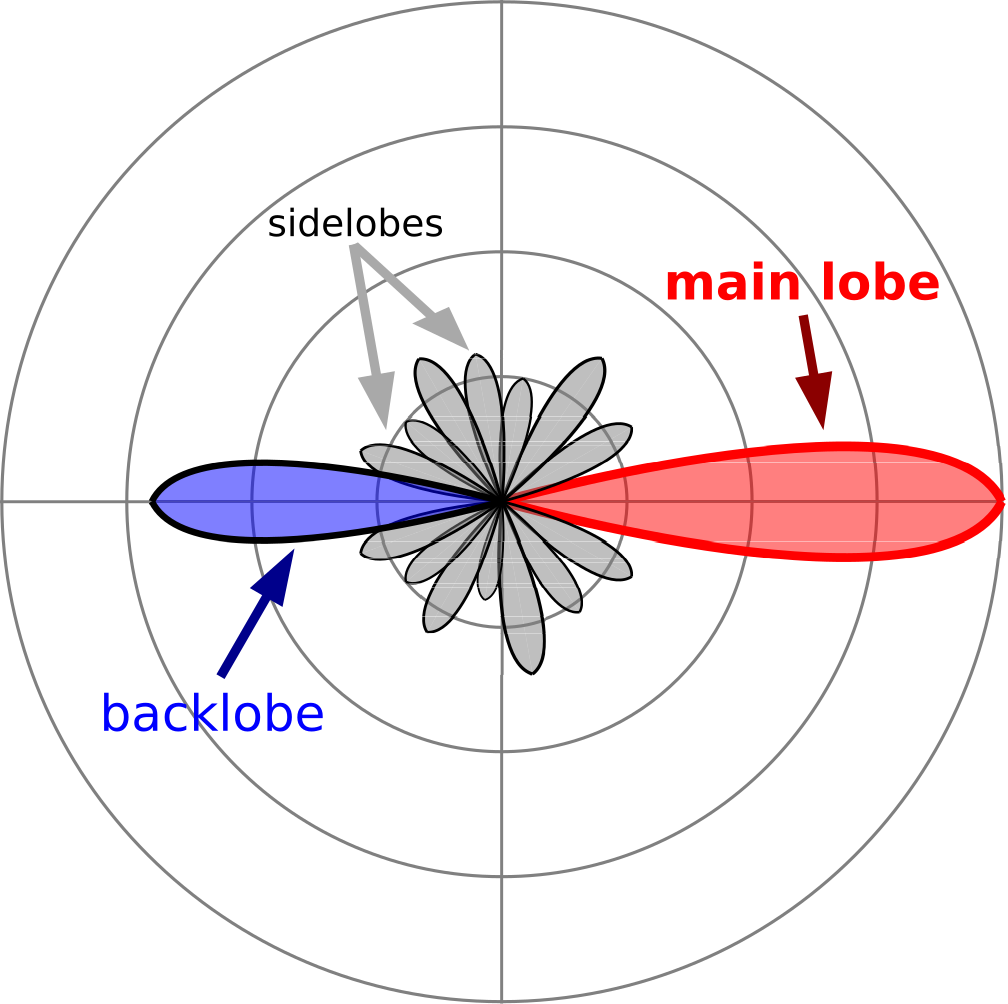
Область навколо напрямку максимальної спрямованості іменується як основна частка. Основна частка обмежена з кожного боку нулем, де величина досягає локального мінімуму, можливо, нуля. Багато антен також демонструють частку в протилежному напрямку, відомий як зворотна лопатка. (Багато інших антен демонструють нуль у цьому напрямку.) Мочки між основною часткою і задньою лопаткою називаються бічними лопатками. Інші часто використовувані метрики шаблону включають перший рівень бічної пелюстки, який є відношенням максимальної величини бічної лепестки, найближчої до основної частки, до основної частки; і відношення передньої частини до спини, яке є відношенням максимальної величини задньої частки до основної частки .

Коли основна частка вузька, прийнято характеризувати візерунок з точки зору половинної потужності ширини променя (HPBW). Це показано на малюнку$\PageIndex{4}$.

Малюнок$\PageIndex{4}$: Половинна потужність ширини променя (HPBW). (CC BY-SA 4.0; S. Lally)

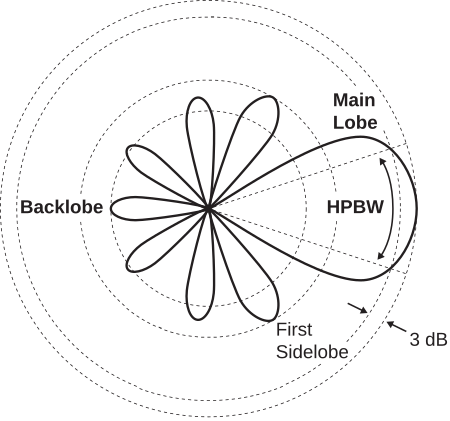
HPBW - ширина основного пелюстки, виміряна між двома точками, в яких спрямованість становить половину її максимального значення. Як метрика шаблону, HPBW залежить від площини, в якій він вимірюється. Зокрема, HPBW може відрізнятися в E- і H-площинами. Наприклад, E-площині HPBW ESD виявляється, що є$90^{\circ}$, тоді як H-площина HPBW не визначена, оскільки картина є постійною в H-площині.

Всеспрямовані та ізотропні антени

ESD є прикладом всенаправленої антени. Всеспрямована антена - це антена, величина малюнка якої номінально постійна в площині, що містить максимальну спрямованість. Для ESD ця площина є H-площиною, тому ESD, як кажуть, є всеспрямованим у H-площині. Термін «всенаправлений» не вказує на постійну закономірність у всіх напрямках. (Насправді, зверніть увагу, що ESD демонструє візерунок нулів у двох напрямках.)

Всеспрямована антена, така як ESD, проявляє постійну і номінально максимальну спрямованість в одній площині.

Антена, малюнок якої рівномірний у всіх напрямках, як кажуть, є ізотропним. Жодна фізично реалізована антена не є ізотропною; насправді, ОУР приблизно так близько, як можна отримати. Тим не менш, концепція «ізотропна антена» корисна як стандарт, на тлі якого інші антени можуть бути кількісно оцінені. Оскільки картина ізотропної антени постійна з напрямком, щільність потужності, що випромінюється такою антеною в будь-якому напрямку, дорівнює щільності потужності, усередненої по всіх напрямках. Таким чином, спрямованість ізотропної антени дорівнює рівно 1. Спрямованість будь-якої іншої антени може бути виражена в одиницях «dBi», що просто дБ відносно ізотропної антени. Наприклад, максимальна спрямованість ОУР становить 1,5, що становить$10\log_{10}\left(1.5/1\right)$$=$ 1,76 дБі. Підводячи підсумки:

Ізотропна антена проявляє постійну спрямованість в кожному напрямку. Така антена фізично не реалізована, але, тим не менш, корисна як базова лінія для опису інших антен.

Додаткове читання:

• «Радіаційна картина» у Вікіпедії.