10.13: Ефективна діафрагма
- Page ID
- 30789
При роботі з системами за участю приймальних антен зручно мати єдиний параметр, який пов'язує падаючу потужність (на відміну від падаючого електричного поля) з потужністю, що подається на електроніку приймача. Цей параметр широко відомий як ефективна діафрагма або діафрагма антени.
З теорії елементарних схем, потужність, що\(Z_L\) подається до навантаження, максимізується, коли навантаження сполучається з імпедансом антени; тобто, коли\(Z_L=Z_A^*\) де\(Z_A\) імпеданс антени. Таким чином, зручне визначення ефективної діафрагми\(A_e\) використовує співвідношення:
\[P_{R,max} \triangleq S^i_{co} A_e \label{m0218_eAedef} \]
де\(S^i_{co}\) щільність падаючої потужності (SI базових одиниць Вт/м\(^2\)), що є спільною поляризацією з антеною, і\(P_{R,max}\) є потужність, що подається на навантаження, яка сполучена узгоджується з антени імпедансу. Підводячи підсумки:
Ефективна апертура (SI базових одиниць м\(^2\)) - це відношення потужності, що подається антеною до сполученого узгодженого навантаження, до падаючої кополяризованої щільності потужності.
Як визначено, метод розрахунку ефективної діафрагми не очевидний, за винятком, можливо, прямого вимірювання. Насправді існує щонайменше три способи обчислити ефективну діафрагму: (а) через ефективну довжину, (b) через термодинаміку та (c) за допомогою взаємності. Кожен з цих методів дає деяку проникливість і розглядаються по черзі.
Ефективна діафрагма через ефективну довжину
Потенціал і струм при навантаженні приймаючої антени можуть бути визначені за допомогою еквівалентної моделі схеми, показаної на малюнку\(\PageIndex{1}\), використовуючи модель еквівалентної схеми Тевенена для антени, розробленої в розділі 10.9.
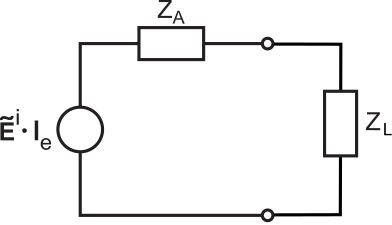
У цій моделі джерело напруги визначається напруженістю падаючого електричного поля\(\widetilde{\bf E}^i\) і вектором\({\bf l_e}=\hat{\bf l}_el_e\) ефективної довжини антени. Визначаємо пов'язану ефективну діафрагму наступним чином. Розглянемо кополяризовану синусоїдально-змінну плоску хвилю,\(\widetilde{\bf E}_{co}^i\) що падає на антену. Далі нехай
\[\widetilde{\bf E}_{co}^i = E^i \hat{\bf e} \nonumber \]
де\(\hat{\bf e}\) - орієнтовний напрямок\(\widetilde{\bf E}_{co}^i\). Кополяризована щільність потужності, що падає на антену, є:
\[S^i_{co} = \frac{\left|E^i\right|^2}{2\eta} \label{m0218_Sico} \]
де\(\eta\) хвильовий опір середовища (наприклад,\(\cong 377~\Omega\) для антени у вільному просторі). У відповідь середня за часом потужність, що подається на навантаження, становить
\[P_R = \frac{1}{2}\mbox{Re}\left\{\widetilde{V}_L \widetilde{I}_L^*\right\} \label{m0218_ePA1} \]
де\(\widetilde{V}_L\) і\(\widetilde{I}_L\) знаходяться потенційні і струмові фазори відповідно при навантаженні. Ми можемо визначити\(\widetilde{V}_L\) і\(\widetilde{I}_L\) з еквівалентної схеми моделі фігури\(\PageIndex{1}\) за допомогою базової теорії схем. Для початку зверніть увагу, що величина і фаза джерела напруги становлять:
\[\widetilde{\bf E}_{co}^i \cdot {\bf l}_e = E^i l_e \left( \hat{\bf e} \cdot \hat{\bf l}_e \right) \nonumber \]
і оскільки ми\(\hat{\bf l}_e\) визначили рівним\(\hat{\bf e}\),
\[\widetilde{\bf E}_{co}^i \cdot {\bf l}_e = E^i l_e \nonumber \]
Далі зверніть увагу, що імпеданс навантаження створює дільник напруги з джерелом (антеною) імпедансом таким чином, що
\[\widetilde{V}_L = \left( E^i l_e \right) \frac{Z_L}{Z_A+Z_L} \nonumber \]
\(\widetilde{I}_L\)Аналогічно, вихідний джерело напруги ділиться на загальний послідовний опір:
\[\widetilde{I}_L = \frac{E^i l_e }{Z_A+Z_L} \nonumber \]
Підставивши ці вирази в Equation\ ref {M0218_EPA1}, отримаємо:
\[P_R = \frac{1}{2} \left|E^i l_e \right|^2 \frac{R_L}{\left|Z_A+Z_L\right|^2} \nonumber \]
Визначимо реальні і уявні складові\(Z_A\) і\(Z_L\) явно, наступним чином:
\[Z_A = R_A +jX_A \nonumber \]
\[Z_L = R_L +jX_L \nonumber \]
Далі припустимо, що втрати внутрішньої антени незначні, так що\(R_A \approx R_{rad}\). Якщо\(Z_L\) сполучений узгоджений для максимальної передачі потужності, то\(Z_L=Z_A^*=R_{rad}-jX_A\). Тому:
\ begin {вирівнювання} P_ {R, max} &=\ розрив {1} {2}\ вліво|e^i l_e\ праворуч |^2\ frac {R_ {рад}} {\ лівий|Z_A+Z_A^*\ праворуч |^2}\ nonumber\\ &=\ frac {1} {2}\ ліворуч | e^2}\ nonumber\\ &=\ frac {1} {2}\ ліворуч | e^i l___е\ праворуч |^2\ гідророзриву {R_ {рад}} {\ ліво|2r_ {рад}\ право|^2}\ nonumber\\ &=\ frac {\ ліво/e^i l_e\ праворуч |^2} {8R_ {rad}}\ мітка {M0219_PRmax}\ кінець {вирівнювання}
Тепер за допомогою рівнянь\ ref {M0218_EaEdeF},\ ref {M0218_Sico} і\ ref {M0219_PRmax}, ми знаходимо:
\[A_e = \frac{\left|E^i l_e \right|^2 / 8R_{rad} }{ \left|E^i\right|^2 / 2\eta } \nonumber \]
що зводиться до:
\[\boxed{ A_e = \frac{ \eta \left|l_e\right|^2 }{ 4 R_{rad} } } \label{m0218_eAeel} \]
Не дивно, що ефективна діафрагма повинна бути пропорційна квадрату величини ефективної довжини. Однак ми бачимо, що середовище та радіаційний опір антени також відіграють певну роль.
Ефективну довжину і радіаційну стійкість легко розрахувати для дротяних антен, тому природно використовувати Equation\ ref {M0218_eAEEL} для обчислення ефективних діафрагм дротяних антен. Для електрично-короткого диполя (ESD) довжини\(L\),\(l_e\approx(L/2)\sin\theta\) і\(R_{rad} \approx 20\pi^2\left(L/\lambda\right)^2\). Таким чином, ми знаходимо ефективну діафрагму, яка передбачає вільний простір (тобто\(\eta=\eta_0\)):
\[A_e \approx 0.119\lambda^2 \left|\sin\theta\right|^2 ~~~\mbox{(lossless ESD)} \nonumber \]
Що примітно, ефективна діафрагма ОУР не залежить від його довжини. Насправді це залежить тільки від частоти експлуатації.
Також варто відзначити, що максимально ефективна діафрагма (тобто ефективна діафрагма в\(\theta=\pi/2\) напрямку)
\[\boxed{ A_e \approx 0.119\lambda^2 } ~~~\mbox{(lossless ESD, max.)} \nonumber \]
Диполі, які не є електрично-короткими, виявляють радіаційну стійкість, яка пропорційна\(L^p\), де\(p>2\). Тому ефективна діафрагма неелектрично-коротких диполів збільшується\(L\), як і очікувалося. Однак це збільшення не є драматичним, якщо не\(L\) є значно більшим\(\lambda/2\). Ось приклад:
Електрично-тонкий напівхвильовий диполь демонструє радіаційну стійкість\(\cong 73~\Omega\) та ефективну довжину\(\lambda/\pi\). Припускаючи, що диполь без втрат і знаходиться у вільному просторі, Equation\ ref {m0218_eAEel} дає:
\[A_e \approx 0.131\lambda^2 ~~~\mbox{(half-wave dipole, max.)} \nonumber \]
Знову ж таки, це ефективна діафрагма для хвилі, що падає від широкої сторони до диполя.
Ефективна діафрагма за допомогою термодинаміки
Корисне розуміння концепції ефективної діафрагми можна зробити, задавши наступне питання: Скільки потужності отримує антена, коли хвилі однакової щільності потужності надходять з усіх боків одночасно? На це питання дивно легко відповісти, використовуючи основні принципи термодинаміки. Термодинаміка - це область фізики, яка стосується тепла та його відношення до випромінювання та електричної енергії. Ніякого попереднього досвіду з термодинамікою в цій деривації не передбачається.
Розглянемо сценарій, зображений на малюнку\(\PageIndex{2}\).
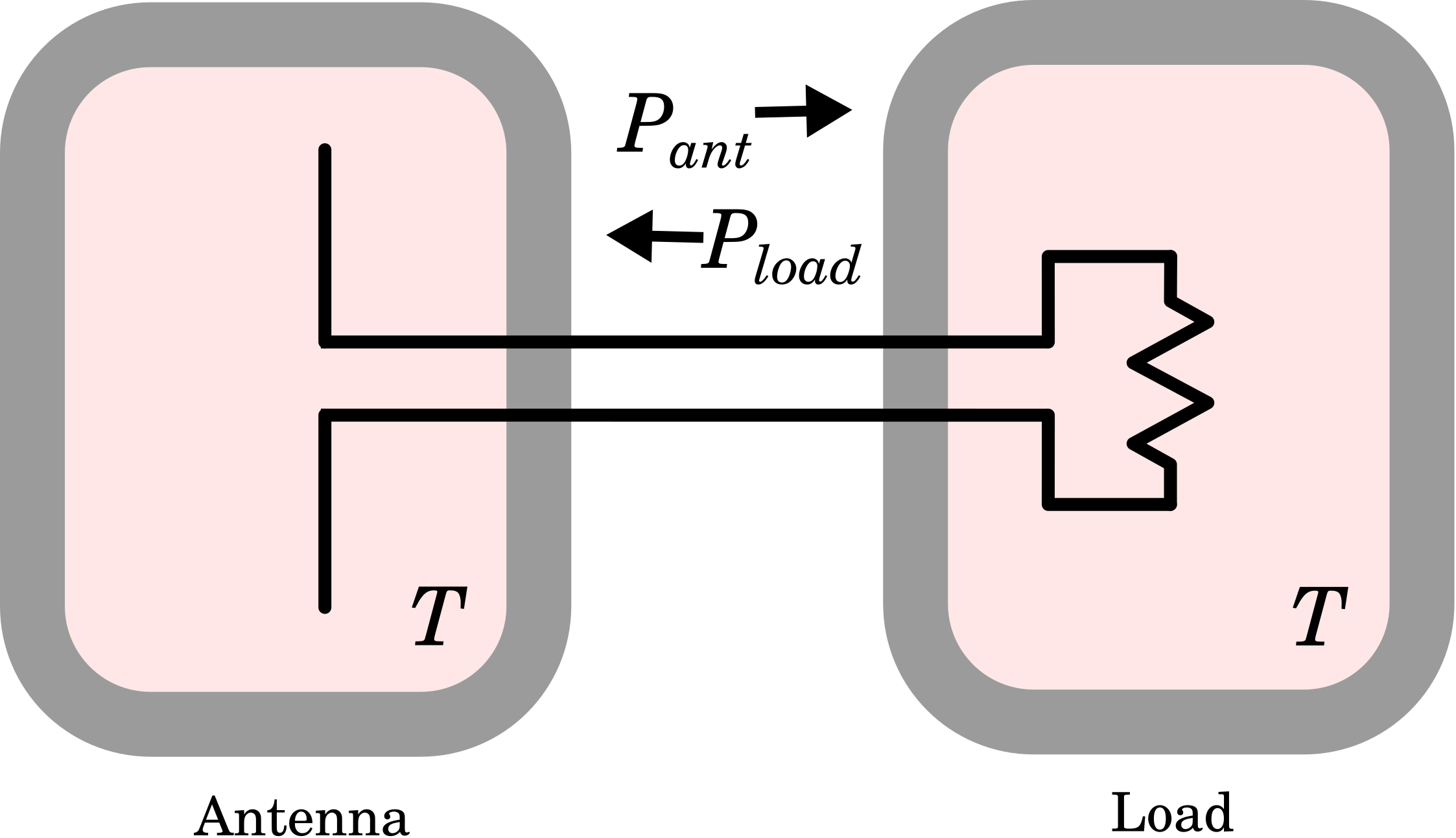
У цьому сценарії антена повністю укладена в камеру, стінки якої не впливають на поведінку антени і мають рівномірну температуру\(T\). Навантаження (як і раніше сполучена з антеною) повністю закрита окремою, але однаковою камерою, також при температурі\(T\).
Розглянемо спочатку завантажувальну камеру. Тепло викликає випадкове прискорення складових носіїв заряду в навантаженні, що породжує випадково мінливий струм на клемах навантаження. (Це відомий як шум Джонсона-Найквіста.) Цей струм, що протікає через навантаження, породжує потенціал; отже, навантаження - незважаючи на те, що є пасивним пристроєм - насправді є джерелом енергії. Потужність, пов'язана з цим шумом, становить:
\[P_{load} = kTB \label{m0218_ePload} \]
де\(k\cong 1.38 \times 10^{-23}\) J/K - постійна Больцмана і\(B\) є пропускною здатністю, в межах якої\(P_{load}\) вимірюється.
Аналогічно антена є джерелом потужності шуму\(P_{ant}\). \(P_{ant}\)також можна інтерпретувати як захоплене теплове випромінювання - тобто електромагнітні хвилі, стимульовані випадковим прискоренням заряджених частинок, що містять стінки камери. Ці хвилі випромінюють від стін і рухаються до антени. Закон термодинаміки Релей-Джинса говорить нам, що це випромінювання повинно мати щільність потужності (тобто базові одиниці СІ Вт/м\(^2\)), рівну
\[\frac{2kT}{\lambda^2}~B \nonumber \]
на стерадіан твердого кута. 1 Загальна потужність, доступна для антени, становить половину цієї суми, оскільки антена чутлива лише до однієї поляризації одночасно, тоді як теплове випромінювання рівномірно розподіляється між будь-якими двома ортогональними поляризаціями. \(P_A\)це решта потужності, отримана шляхом інтеграції над усіма\(4\pi\) стерадіанами. Тому антена захоплює сумарну потужність, рівну 2
\ begin {вирівняти} P_ {мураха} &=\ точка {a_e (\ тета ',\ фі')\ лівий (\ frac {1} {2} ~\ frac {2kT} {\ лямбда-^2} ~B\ праворуч)\ sin\ theta' d\ theta' d\ phi'}\ nonnumber\ &=\ left (\ frac {kT}\ лямбда ^ 2} ~B\ право)\ точка {a_e (\ тета ',\ фі')\ sin\ тета' d\ phi '}\ етикетка {m0218_ePant}\ end {вирівняти}
Враховуючи умови експерименту, і зокрема, оскільки антенна камера і камера навантаження знаходяться при однаковій температурі, антена і навантаження знаходяться в термодинамічній рівновазі. Наслідком цієї рівноваги є те, що потужність,\(P_{ant}\) захоплена антеною і поставлена на навантаження, повинна дорівнювати потужності, що\(P_{load}\) генерується навантаженням і доставляється на антену; т. Е.
\[P_{ant} = P_{load} \label{m0218_eTE} \]
Об'єднавши рівняння\ ref {M0218_Epload},\ ref {M0218_epant} і\ ref {M0218_ete}, отримаємо:
\[\left(\frac{kT}{\lambda^2}~B \right) \oint { A_e(\theta',\phi') \sin\theta' d\theta' d\phi' } = kTB \nonumber \]
що зводиться до:
\[\oint { A_e(\theta',\phi') \sin\theta' d\theta' d\phi' } = \lambda^2 \label{m0218_fAT1} \]
\(\left<A_e\right>\)Дозволяти бути середня ефективна діафрагма антени; тобто,\(A_e\) усереднений по всіх можливих напрямках. Це середнє значення просто рівняння\ ref {m0218_fat1} ділиться на\(4\pi\) sr твердого кута, що містить всі можливі напрямки. Таким чином:
\[\left<A_e\right> = \frac{\lambda^2}{4\pi} \nonumber \]
Нагадаємо, що ізотропна антена - це та, яка має однакову ефективну діафрагму в кожному напрямку. Таких антен на практиці не існує, але концепція ізотропної антени досить корисна, як ми скоро побачимо. Оскільки ефективна діафрагма ізотропної антени повинна бути такою ж, як і її середня ефективна діафрагма, ми знаходимо:
\[\boxed{ A_e = \frac{\lambda^2}{4\pi} \approx 0.080\lambda^2 ~~~\mbox{(isotropic antenna)} } \nonumber \]
Зверніть увагу далі, що це повинно бути мінімально можливим значенням максимально ефективної діафрагми для будь-якої антени.
Ефективна діафрагма за допомогою взаємності
Той факт, що всі антени мають максимально ефективну діафрагму більше, ніж у ізотропної антени, робить ізотропну антену логічним орієнтиром, з яким можна порівняти ефективну діафрагму антен. Ми можемо охарактеризувати ефективну діафрагму будь-якої антени як деяку безроздільну реальну постійну кількість\(D\) разів ефективної діафрагми ізотропної антени; тобто:
\[\boxed{ A_e \triangleq D \frac{\lambda^2}{4\pi} ~~~\mbox{(any antenna)} } \label{m0218_eAe1} \]
де\(D\) має бути більше або дорівнює 1.
Проникливі читачі можуть помітити, що\(D\) здається дуже схожим на спрямованість. Спрямованість визначається в розділі 10.7 як фактор, за допомогою якого передавальна антена збільшує щільність потужності свого випромінювання над тією ізотропної антени. Давайте ще раз розглянемо ОУР, для якого ми раніше визначили (через ефективну концепцію довжини), що\(A_e\cong 0.119\lambda^2\) в тому напрямку, в якому вона максимальна. Застосовуючи рівняння\ ref {M0218_EaE1} до ОУР, знаходимо:
\[D \triangleq A_e \frac{4\pi}{\lambda^2} \cong 1.50 ~~~\mbox{(ESD, max.)} \nonumber \]
Звичайно,\(D\) дорівнює спрямованості ОУР у випадку передачі.
Цей результат виявляється в цілому вірним; тобто:
Ефективна діафрагма будь-якої антени задається рівнянням\ ref {\(D\)M0218_EAE1} де спрямованість антени при передачі.
Виведення цього результату для загального випадку можливе за допомогою аналізу, подібного до термодинаміки, представленої раніше, або за допомогою теореми взаємності, розробленої в розділі 10.10.
Той факт, що ефективна діафрагма легко обчислюється від спрямованості передачі є надзвичайно корисним інструментом в антенній інженерії. Без цього інструменту визначення ефективної діафрагми обмежується прямим вимірюванням або розрахунком за допомогою ефективної довжини; і ефективну довжину, як правило, важко обчислити для антен, які не дуже добре описані як розподіли струму вздовж лінії. Зазвичай набагато простіше обчислити спрямованість антени при передачі, а потім використовувати Equation\ ref {M0218_EaE1} для отримання ефективної діафрагми для роботи прийому.
Відзначимо, що цей принцип сам по собі є виразом взаємності. Тобто, можна справедливо сказати, що «спрямованість» - це не виключно концепція передачі, ні концепція прийому, а скоріше є єдиною кількісною характеристикою антени, яка застосовується як у випадку передачі, так і прийому. Нагадаємо, що діаграми випромінювання використовуються для кількісної оцінки способу (передачі) спрямованості змінюється залежно від напрямку. Раптом ми виявили, що точно такі ж шаблони застосовуються до випадку отримання! Підводячи підсумки:
Поки виконуються умови, необхідні для формальної взаємності, спрямованість приймальної антени (визначена за допомогою Equation\ ref {M0218_EaE1}) дорівнює спрямованості тієї ж антени при передачі, а шаблони, що описують спрямованість прийому, рівні тим, що для спрямованості передачі.
Нарешті, ми зауважимо, що еквівалентність спрямованості передачі та прийому може, знову ж таки за допомогою Equation\ ref {M0218_EAE1}, бути використана для визначення ефективної діафрагми для випадку передачі. Іншими словами, ми можемо визначити ефективну діафрагму передавальної антени, щоб бути в\(\lambda^2/4\pi\) рази спрямованість антени. Тут немає нової фізики; ми просто користуємося тим, що поняття ефективної діафрагми та спрямованості описують по суті ту ж характеристику антени, і що ця характеристика однакова як для передачі, так і для прийому операції.
- Повне розкриття: Це наближення до точного виразу, але дуже точне на радіочастотах. Додаткові відомості див. в розділі «Додаткове читання» в кінці цього розділу. ↩
- Нагадаємо\(\sin\theta' d\theta' d\phi'\), це диференціальний елемент твердого кута. ↩
