10.11: Потенціал, індукований у диполі

Електромагнітна хвиля, що падає на антену, буде викликати потенціал на клемах антени. У цьому розділі ми виведемо цей потенціал. Для спрощення виведення розглянемо окремий випадок прямого тонкого диполя довільної довжини, який освітлюється плоской хвилею. Однак певні аспекти деривації стосуватимуться антен загалом. Зокрема, поняття ефективної довжини (також відомої як ефективна висота) та ефективна довжина вектора виникають природно з цього похідного, тому цей розділ також служить сходинкою у розробці еквівалентної моделі схеми для приймальної антени. Походження спирається на передавальні властивості диполів, а також принцип взаємності, тому перед читанням цього розділу рекомендується ознайомитися з цими темами.

Сценарій, що цікавить, зображений на малюнку$\PageIndex{1}$. Тут тонкий$\hat{\bf z}$ вирівняний прямий диполь розташований біля початку. Загальна довжина диполя дорівнює$L$. Руки диполя ідеально-провідні. Клеми складаються з невеликого зазору довжини$\Delta l$ між плечима. Падаюча плоска хвиля описується з точки зору напруженості її електричного поля$\widetilde{\bf E}^i$. Питання таке: Що таке$\widetilde{V}_{OC}$, потенціал на клемах при розімкнутих клемах?

Малюнок$\PageIndex{1}$: Потенціал індукується на клемах тонкого прямого диполя у відповідь на падаючу площину хвилі. (CC BY-SA 4.0; C. Ван)

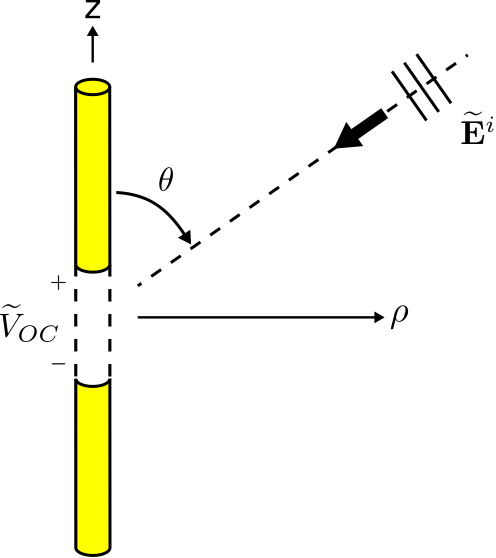
Існує кілька підходів до вирішення цієї проблеми. Пряма атака полягає в тому, щоб викликати принцип, що потенціал дорівнює інтегралу напруженості електричного поля на шляху. В цьому випадку шлях починається у терміналу «$-$» і закінчується у терміналу «$+$», перетинаючи зазор, який визначає клеми антени. Таким чином:

$$\widetilde{V}_{OC} = -\int_{gap} \widetilde{\bf E}_{gap} \cdot d{\bf l} \label{m0215_eVoc-General}$$

де$\widetilde{\bf E}_{gap}$ - електричне поле в зазорі. Проблема при такому підході полягає в тому, що значення не$\widetilde{\bf E}_{gap}$ легко доступне. Це не просто$\widetilde{\bf E}^i$, тому що структура антени (зокрема, електромагнітні граничні умови) змінюють електричне поле в безпосередній близькості від антени. ¹

На щастя, ми можемо обійти цю перешкоду, використовуючи принцип взаємності. У стратегії, заснованої на взаємності, ми встановлюємо взаємозв'язок між двома сценаріями, які відбуваються в межах однієї електромагнітної системи. Перший сценарій показаний на малюнку$\PageIndex{2}$.

Малюнок$\PageIndex{2}$: Диполь інтересу, керований струмом$\widetilde{\mathbf{E}_{1}}$,$\widetilde{I}_{1}^{t}$ випромінює електричне поле, в результаті чого потенціал розімкнутого ланцюга$\widetilde{V}_{2}^{r}$ на клемах диполя Герца в дальньому полі. (CC BY-SA 4.0; C. Ван)

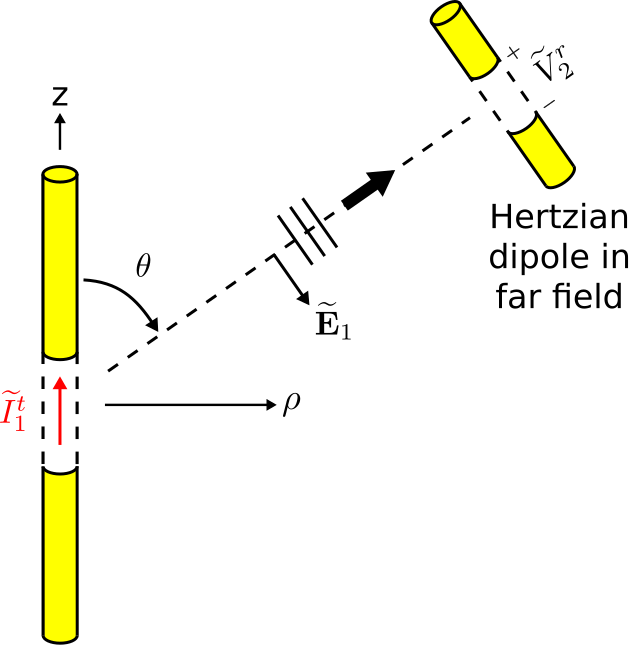
У цьому випадку у нас є два диполя. Перший диполь - це саме диполь цікавить (рис.$\PageIndex{1}$), за винятком того, що струм$\widetilde{I}_1^t$ подається на клеми антени. Це породжує розподіл струму$\widetilde{I}(z)$ (базові одиниці СІ A) уздовж диполя, а згодом диполь випромінює електричне поле (Розділ 9.6):

\ begin {вирівнювання}\ widetilde {\ bf E} _1 ({\ bf r}) &\ приблизно\ капелюх {\ bf\ тета} j\ frac {\ eta} {2}\ frac {-j\ бета-р}} {r} ~\ лівий (\ sin\ тета\ правий)\ nonumber\ ~ ~ ~\ cdot\ left\ frac [c {1} {\ лямбда}\ int_ {-L/2} ^ {+L/2}\ widetilde {I} (z') e^ {+j\ бета z '\ cos {\ тета}} дз'\ праворуч]\ мітка {m0215_eesde}\ кінець {вирівнювання}

Друга антена$\hat{\bf \theta}$ - вирівняний герцианський диполь у далекому полі, який приймає$\widetilde{\bf E}_1$. (Для ознайомлення з властивостями диполів Герціана див. Розділ 9.4. Ключовим моментом є те, що диполі Герціана зникають мало.) Зокрема, ми вимірюємо (принаймні концептуально) потенціал розімкнутого ланцюга$\widetilde{V}_2^r$ на клемах диполя Герца. Для цієї мети ми вибираємо диполь Герца, тому що - на відміну від по суті всіх інших антен - легко визначити потенціал розімкнутої ланцюга. Як пояснювалося раніше:

$$\widetilde{V}_2^r = -\int_{gap} \widetilde{\bf E}_{gap} \cdot d{\bf l} \nonumber$$

Для диполя Герціана$\widetilde{\bf E}_{gap}$ - це просто падаюче електричне поле, оскільки існує незначна структура (зокрема, незначна кількість матеріалу), присутня для зміни електричного поля. Таким чином, ми маємо просто:

$$\widetilde{V}_2^r = -\int_{gap} \widetilde{\bf E}_1 \cdot d{\bf l} \label{m0215_eV2r1}$$

Оскільки диполь Герца дуже короткий і дуже далеко від передавального диполя,$\widetilde{\bf E}_1$ по суті постійний над розривом. Також нагадаємо, що ми вимагали, щоб Герцианський диполь був вирівняний з$\widetilde{\bf E}_1$. Вибір інтеграції по прямій лінії через проміжок, Equation\ ref {M0215_Ev2r1} зводиться до:

$$\widetilde{V}_2^r = -\widetilde{\bf E}_1({\bf r}_2) \cdot \hat{\bf \theta}\Delta l \label{m0215_eV2r2}$$

де$\Delta l$ - довжина щілини і${\bf r}_2$ - розташування герціановского диполя. Підставивши вираз для$\widetilde{\bf E}_1$ з Equation\ ref {M0215_eesde}, отримаємо:

\ begin {вирівнювання}\ widetilde {V} _2^r\ приблизно &- j\ frac {\ eta} {\ eta} {2}\ frac {-j\ бета r_2}} {r_2} ~\ ліворуч (\ sin\ тета\ праворуч)\ nonumber\\ ~ ~ ~\ cdot\ ліворуч [\ frac {1} {\ лямбда}\ int_ -L/2} ^ {+L/2}\ широкий {I} (z') e^ {+j\ бета z '\ cos {\ тета}} дз'\ праворуч]\ дельта л\ мітка {m0215_ev2r3}\ кінець {вирівнювання}

де$r_2=\left|{\bf r}_2\right|$.

Малюнок$\PageIndex{3}$: Диполь Герца, що приводиться в дію струмом Iet,$\widetilde{I}_2^t$ випромінює електричне поле$\widetilde{\mathbf{E}}_{2}$, в результаті чого потенціал розімкнутого ланцюга$\widetilde{V}_{1}^{r}$ на клемах цікавить диполя. (CC BY-SA 4.0; C. Ван)

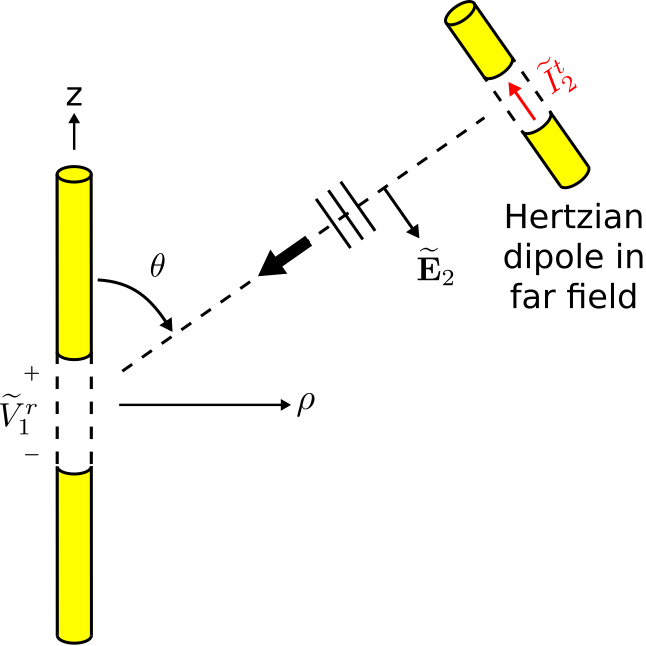
Другий варіант розвитку подій показаний на малюнку$\PageIndex{3}$. Цей сценарій ідентичний першому сценарію, за винятком того, що диполь Герціана передає і диполь цікавить. Поле, випромінюване диполем Герца у відповідь на застосований струм$\widetilde{I}_2^t$, оцінений за початком, становить (розділ 9.4):

$$\widetilde{\bf E}_2({\bf r}=0) \approx \hat{\bf \theta} j\eta \frac{\widetilde{I}_2^t\cdot\beta \Delta l}{4\pi}~(1)~\frac{e^{-j\beta r_2}}{r_2} \label{m0215_eE}$$

Коефіцієнт «$\sin\theta$» в загальному виразі дорівнює 1 в даному випадку, так як$\PageIndex{3}$, як показано на малюнку, походження розташовується широкою стороною (тобто при$\pi/2$ рад) щодо осі диполя Герца. Також зауважте, що оскільки герцианський диполь, як передбачається, знаходиться в далекому полі,${\bf E}_2$ може бути інтерпретований як плоска хвиля в області приймаючого диполя, що цікавить.

Тепер ми запитуємо: Який індукований потенціал$\widetilde{V}_1^r$ в диполі цікавить? Знову ж таки, Equation\ ref {M0215_Evoc-general} не сильно допомагає, тому що електричне поле в проміжку не відомо. Однак ми знаємо, що це$\widetilde{V}_1^r$ повинно бути пропорційним$\widetilde{\bf E}_2({\bf r}=0)$, оскільки це вважається лінійною системою. Виходячи з цієї великої кількості інформації, повинен бути певний вектор,${\bf l}_e=\hat{\bf l} l_e$ для якого

$$\widetilde{V}_1^r = \widetilde{\bf E}_2({\bf r}=0) \cdot {\bf l}_e \label{m0215_eVEL1}$$

Це не однозначно визначає$\hat{\bf l}$ ні одиничний вектор$l_e$, ні скалярну частину, так як зміна визначення першого може компенсуватися зміною визначення останньої і навпаки. Таким чином, на даний момент ми викликаємо стандартне визначення${\bf l}_e$ як вектора ефективної довжини, введеного в Розділі 10.9. Таким чином,$\hat{\bf l}$ визначається напрямок, в якому електричне поле, передане від антени, було б поляризоване. У цьому прикладі$\hat{\bf l}=-\hat{\bf \theta}$, де знак мінус відображає той факт, що позитивний термінальний потенціал призводить до термінального струму, який тече в$-\hat{\bf z}$ напрямку. Таким чином, рівняння\ ref {M0215_Evel1} стає:

$$\widetilde{V}_1^r = -\widetilde{\bf E}_2({\bf r}=0) \cdot \hat{\bf \theta} l_e \nonumber$$

Ми можемо піти трохи далі і підставити вираз для$\widetilde{\bf E}_2({\bf r}=0)$ з Equation\ ref {M0215_ee}:

$$\widetilde{V}_1^r \approx - j\eta~\frac{\widetilde{I}_2^t\cdot\beta \Delta l}{4\pi}~\frac{e^{-j\beta r_2}}{r_2} l_e \label{m0215_eV1r1}$$

Тепер ми закликаємо взаємність. Як двопортова лінійна інваріантна система часу, повинна бути правдою, що:

$$\widetilde{I}_1^t \widetilde{V}_1^r = \widetilde{I}_2^t \widetilde{V}_2^r \nonumber$$

Таким чином:

$$\widetilde{V}_1^r = \frac{\widetilde{I}_2^t}{\widetilde{I}_1^t} \widetilde{V}_2^r \nonumber$$

Підставляємо вираз для$\widetilde{V}_2^r$ з Рівняння\ ref {M0215_Ev2r3}:

$$\begin{aligned} \widetilde{V}_1^r \approx &- \frac{\widetilde{I}_2^t}{\widetilde{I}_1^t} \cdot j \frac{\eta}{2} \frac{e^{-j\beta r_2}}{r_2}~\left(\sin\theta\right) \nonumber \\ & ~~~\cdot\left[\frac{1}{\lambda}\int_{-L/2}^{+L/2} \widetilde{I}(z') e^{+j\beta z'\cos{\theta}} dz'\right] \Delta l\end{aligned} \nonumber$$

Таким чином, взаємність забезпечила другий вираз для$\widetilde{V}_1^r$. Ми можемо вирішити for,$l_e$ встановивши цей вираз рівним виразу з Equation\ ref {M0215_ev1r1}, що дає

$$l_e \approx \frac{2\pi}{\beta \widetilde{I}_1^t} \left[\frac{1}{\lambda}\int_{-L/2}^{+L/2} \widetilde{I}(z') e^{+j\beta z'\cos{\theta}} dz'\right] \sin\theta \nonumber$$

Відзначивши$\beta=2\pi/\lambda$, що це спрощує:

$$l_e \approx \left[ \frac{1}{\widetilde{I}_1^t}\int_{-L/2}^{+L/2} \widetilde{I}(z') e^{+j\beta z'\cos{\theta}} dz' \right] \sin\theta \label{m0215_ele}$$

Таким чином, зробити розрахунок можна$l_e$ за допомогою наступної процедури:

1. Застосуйте струм$\widetilde{I}_1^t$ до диполя, що цікавить.
2. Визначте отриманий розподіл струму$\widetilde{I}(z)$ по довжині диполя. (Зверніть увагу, що саме це робиться для електрично-короткого диполя в розділі 9.5 та для напівхвильового диполя в розділі 9.7.)
3. Інтегруйте$\widetilde{I}(z)$ по довжині диполя, як зазначено в Equation\ ref {m0215_ele}. Потім розділити («нормалізувати») на$\widetilde{I}_1^t$ (що просто$\widetilde{I}(0)$). Зверніть увагу, що результат не залежить від збудження$\widetilde{I}_1^t$, як і очікувалося, оскільки це лінійна система.
4. Помножити на$\sin\theta$.

Тепер ми визначили, що потенціал клеми відкритого ланцюга$\widetilde{V}_{OC}$ у відповідь на падаюче електричне поле$\widetilde{\bf E}^i$ дорівнює

$$\boxed{ \widetilde{V}_{OC} = \widetilde{\bf E}^i \cdot {\bf l}_e } \label{m0215_eVOCEL}$$

де${\bf l}_e = \hat{\bf l} l_e$ - ефективна довжина вектора, визначена раніше.

Цей результат є чудовим. Простою англійською мовою ми виявили, що:

Потенціал, індукований у диполі, є кополяризованою складовою падаючого електричного поля разів нормованим інтегралом розподілу струму передачі по довжині диполя, разів синус кута між віссю диполя та напрямком падіння.

Іншими словами, властивість взаємності лінійних систем дозволяє визначити цю властивість приймальної антени відносно легко, якщо відомі характеристики передачі антени.

Приклад$\PageIndex{1}$: Effective length of a thin electrically-short dipole (ESD)

Як пояснюється в розділі 9.5, розподіл струму на тонкому ОУР

$$\widetilde{I}(z) \approx I_0 \left(1-\frac{2}{L}\left|z\right|\right) \nonumber$$

де$L$ - довжина диполя і$I_0$ - термінальний струм. Застосовуючи рівняння\ ref {m0215_ele}, знаходимо:

$$\begin{aligned} l_e \approx & \left[ \frac{1}{I_0}\int_{-L/2}^{+L/2} I_0 \left(1-\frac{2}{L}\left|z'\right|\right) e^{+j\beta z'\cos{\theta}} dz' \right] \nonumber \\ &\cdot \sin\theta\end{aligned} \nonumber$$

Нагадаємо$\beta=2\pi/\lambda$, так$\beta z'=2\pi\left(z'/\lambda\right)$. Оскільки це електрично-короткий диполь,$z' \ll \lambda$ над усім інтегралом, і згодом ми можемо припустити$e^{+j\beta z'\cos{\theta}}\approx 1$ над усім інтегралом. Таким чином:

$$l_e \approx \left[ \int_{-L/2}^{+L/2} \left(1-\frac{2}{L}\left|z'\right|\right) dz' \right] \sin\theta \nonumber$$

Інтеграл легко вирішується стандартними методами, або просто визнати, що «площа під кривою» в даному випадку просто на половину «base» ($L$) рази «height» ($1$). Так чи інакше, ми знаходимо

$$l_e\approx \frac{L}{2} \sin\theta \nonumber$$

Приклад 10.9.1 (розділ 10.9) демонструє, як Equation\ ref {M0215_Evocel} з ефективною довжиною вектора, визначеною в попередньому прикладі, використовується для отримання індукованого потенціалу.

---

1. Крім того, якби це було правдою, то сама антена не мала б значення; лише відносний інтервал та орієнтація антенних терміналів мали б значення! ↩