10.14: Рівняння передачі Friis
- Page ID
- 30790
Загальним завданням у додатках радіосистем є визначення потужності, що подається приймачу через віддалений передавач. Сценарій показаний на малюнку\(\PageIndex{1}\):
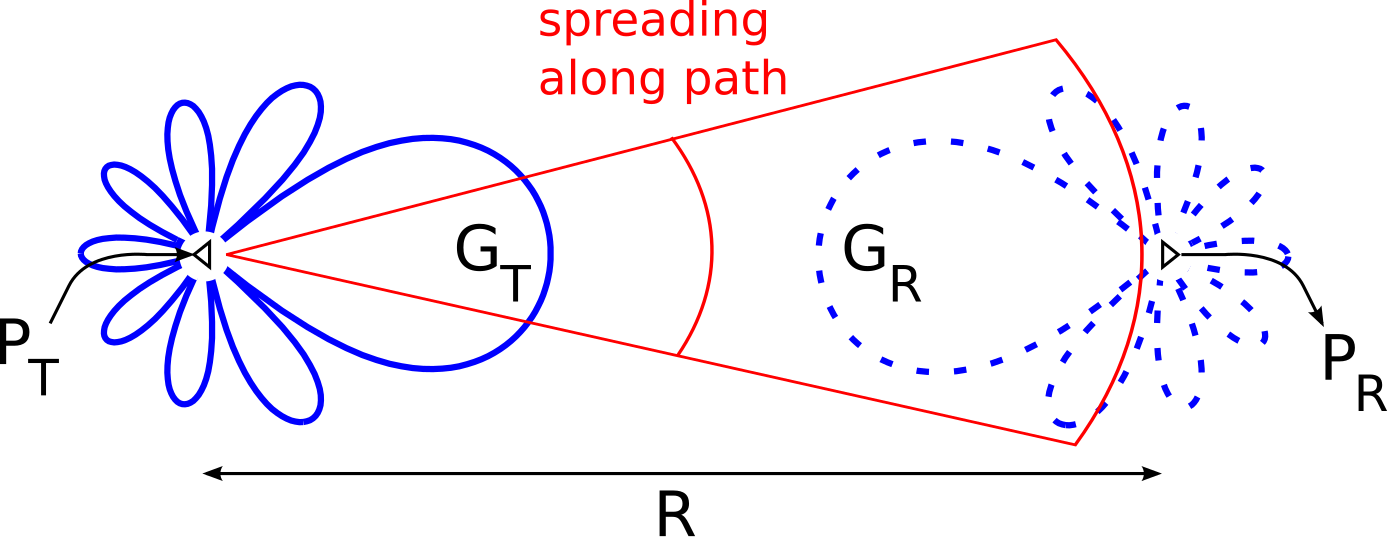
Передавач подає живлення\(P_T\) на антену, яка має посилення\(G_T\) в напрямку приймача. Антена приймача має коефіцієнт посилення\(G_R\). Як завжди, коефіцієнт посилення антени дорівнює спрямованості разів ефективності випромінювання, тому\(G_T\) і\(G_R\) враховувати втрати всередині антени, але не втрати через невідповідність імпедансу.
Простий вираз для\(P_R\) можна вивести наступним чином. По-перше, припустимо «умови вільного простору»; тобто припустимо, що втручається місцевість демонструє незначне поглинання, відображення або інше розсіювання переданого сигналу. У цьому випадку просторова щільність потужності в діапазоні\(R\) від передавача, який випромінює цю потужність через антену без втрат та ізотропної, буде:
\[\frac{P_T}{4\pi R^2} \nonumber \]
тобто сумарна передана потужність ділиться на площу сфери радіуса,\(R\) через яку повинна протікати вся потужність. Фактична щільність потужності\(S^i\) - це кількість разів коефіцієнт посилення передавальної антени, тобто:
\[S^i = \frac{P_T}{4\pi R^2} G_T \nonumber \]
Максимальна прийнята потужність - це падаюча кополяризована щільність потужності, що перевищує ефективну діафрагму\(A_e\) приймальної антени:
\ begin {вирівнювання} P_ {R, max} &= a_e S^i_ {co}\ nonumber\\ nonumber\ &= a_e\ розриву {P_T} {4\ пі R^2} G_T\ мітка {m0219_epRMax1}\ кінець {вирівняти}
Це передбачає, що приймаюча антена співполяризована з падаючим електричним полем, і що приймач сполучений з антеною. Ефективна діафрагма також може бути виражена з точки зору\(G_R\) коефіцієнта посилення приймаючої антени:
\[A_e = \frac{\lambda^2}{4\pi} G_R \nonumber \]
Таким чином, рівняння\ ref {M0219_EPRmax1} може бути записано в такому вигляді:
\[\boxed{ P_{R,max} = P_T G_T \left(\frac{\lambda}{4\pi R}\right)^2 G_R } \label{m0219_eFTE} \]
Це рівняння передачі Фрііса. Підводячи підсумки:
Рівняння передачі Фрііса (Equation\ ref {M0219_EFTE}) дає потужність, що подається на сполучений узгоджений приймач у відповідь на віддалений передавач, припускаючи кополяризовані антени та умови вільного простору.
Коефіцієнт,\(\left(\lambda/4\pi R\right)^2\) що з'являється у рівнянні передачі Фрііса, називається посиленням шляху вільного простору. Найчастіше це виражається у вигляді зворотної величини:
\[\boxed{ L_p \triangleq \left(\frac{\lambda}{4\pi R}\right)^{-2} } \nonumber \]
який відомий як втрата вільного простору. Таким чином, рівняння\ ref {M0219_EFTE} може бути виражено наступним чином:
\[P_{R,max} = P_T G_T L_p^{-1} G_R \label{m0219_eFTE2} \]
Корисність поняття втрати шляху полягає в тому, що вона також може бути визначена для умов, відмінних від вільного простору. Рівняння передачі Фрііса все ще застосовується; просто використовується відповідне (і, ймовірно, значно відрізняється) значення\(L_p\).
Поширеною помилкою є те, що втрата шляху дорівнює зменшенню щільності потужності через поширення по шляху між антенами, і тому ця «втрата поширення» збільшується з частотою. По суті, зниження щільності потужності внаслідок розкидання між будь-якими двома відстанями\(R_1 < R_2\) є:
\[\frac{P_T/4\pi R_1^2}{P_T/4\pi R_2^2} = \left(\frac{R_1}{R_2}\right)^2 \nonumber \]
яка явно не залежить від частоти. Втрата шляху\(L_p\), навпаки, залежить тільки від загальної відстані\(R\) і залежить від частоти. Залежність від частоти відображає залежність ефективної діафрагми від довжини хвилі. Таким чином, втрата шляху не є втратою в традиційному розумінні, а скоріше враховує поєднання поширення та\(\lambda^2\) залежність ефективної діафрагми, яка є спільною для всіх приймальних антен.
Нарешті, зауважте, що Equation\ ref {M0219_EFTE2} є лише найпростішою формою рівняння передачі Фрііса. Часто зустрічаються\(G_R\) альтернативні форми включають форми, в яких\(G_T\) та/або замість них представлені пов'язані ефективні діафрагми, і форми, в яких враховуються наслідки невідповідності опору антени та/або крос-поляризації.
Наземні телекомунікаційні системи зазвичай агрегують велику кількість окремих комунікаційних зв'язків в один канал з високою пропускною здатністю. Це часто реалізується як радіозв'язок між антенами типу посуду, що мають коефіцієнт посилення близько\(27\) dBi (це дБ щодо ізотропної антени без втрат), встановлених на дуже високих вежах і працюють на частотах близько 6 ГГц. Якщо припустити, що мінімально прийнятна потужність прийому дорівнює\(-120\) дБм (це\(-120\) дБ щодо 1\(10^{-15}\) мВт; тобто Вт), а необхідний діапазон 30 км, яка мінімально прийнятна потужність передачі?
Рішення
З постановки проблеми:
\[G_T=G_R=10^{27/10}\cong 501 \nonumber \]
\[\lambda =\frac{c}{f} \cong \frac{3 \times 10^8~\mbox{m/s}}{6 \times 10^9~\mbox{Hz}} \cong 5.00~\mbox{cm} \nonumber \]
\(R=30\)км і\(P_R\ge 10^{-15}\) Вт. Ми припускаємо, що висота і висока спрямованість антен дають умови досить близькі до вільного простору. Далі ми припускаємо сполучення узгодження на приймачі, і що антени кополяризовані. За цих умов застосовується\(P_R=P_{R,max}\) і рівняння\ ref {M0219_EFTE}. Знаходимо:
\[\begin{aligned} P_T &\ge \frac{ P_{R,max} }{ G_T \left(\lambda/4\pi R\right)^2 G_R } \\ &\cong 2.26 \times 10^{-7}~\mbox{W} \nonumber \\ &\cong 2.26 \times 10^{-4}~\mbox{mW} \nonumber \\ &\cong \underline{-36.5~\mbox{dBm}} \nonumber\end{aligned} \nonumber \]
Додаткове читання:
- «Втрата шляху вільного простору» у Вікіпедії.
- «Рівняння передачі Фрііса» у Вікіпедії.
