3: Додаткові інструменти аеродинаміки

Вступ

Усі вступні аеродинамічні концепції, необхідні для матеріалу виконання літака, які повинні бути висвітлені в наступних розділах, були представлені в главі 1. Загалом, на вибір читачів залишиться багато чудових текстів на тему аеродинаміки, щоб забезпечити поглиблене висвітлення поля, включаючи повне виведення аеродинамічних теорій та обговорення їх використання. Поле аеродинаміки часто розділяється на п'ять або більше сегментів на основі характеристик потоку та припущень, які можуть або повинні бути зроблені для детального аналізу цих потоків. Ці підрозділи, як правило, включають:

• Нестислива або дозвукова аеродинаміка
• Транзвукова аеродинаміка
• Надзвукова аеродинаміка
• Гіперзвукова аеродинаміка
• Теорія прикордонного шару

Інші, ще більш спеціалізовані, сегменти аеродинамічного поля можуть включати такі теми, як динаміка розрідженого газу та магнітогідродинаміка.

У першій главі ми розглянули кілька основних понять, що стосуються перших трьох тем вище, з акцентом на режим нестисливого потоку і, сподіваємось, достатнє обговорення припущень, пов'язаних з тим, щоб читач міг визнати, коли йому чи їй загрожує необхідність обліку трансзвукового або надзвукового потоку. ефекти. Ми розглянули деякі основні висновки, які виходять з аналізу дво- і тривимірного течії навколо аеропланів і крил. Ми дізналися, наприклад, що розвал аеропрофілю визначатиме кут атаки, при якому коефіцієнт підйому аеродрому дорівнює нулю, і що ми можемо тимчасово змінити розвал з такими речами, як крило викривлення або його сучасний еквівалент, «морфінг», або, більш традиційним способом з клапанами. Нам може бути цікаво, скільки зміни розвалу може дати в нульовому куті підйому атаки.

Ми дізналися, що існує певний тип розподілу підйому на тривимірному крилі, який дасть «оптимальні» аеродинамічні показники, надаючи «мінімальний індукований опір», і ми виявили, що більш високі пропорції форми крила також дають кращу продуктивність, ніж крила з низькою AR.

У цій главі ми збираємось дуже елементарно поглянути на ці два фундаментальні ефекти конфігурації крила та аеропрофілю, достатньо погляду, щоб ми мали принаймні один-два основних інструменти, які могли б допомогти нам дізнатися щось про вплив дизайну крила на продуктивність літаків, якщо нам потрібно це зробити. Ми зробимо це не через тип ретельного аналізу, який був би знайдений у більшості хороших аеродинамічних підручників, а з парою дещо більш спрощених підходів, які, тим не менш, часто корисні.

Для того, щоб розробити бажані методи «задньої частини конверта» для розгляду деяких основних впливів аеродинаміки та форми крила на аеродинаміку та продуктивність, нам потрібно спочатку швидко поглянути на те, як аеродинамік зробить математичну модель крила або аеродинаміки. Почнемо з того, що подивимося на потік навколо підйомного аерокрила.

3.1 Аеродинаміка (2-D аеродинаміка)

Для аерокрила або крила для підйому продукту потік над його верхньою поверхнею повинен рухатися швидше, ніж потік над його нижньою поверхнею. Якщо це станеться, рівняння Бернуллі скаже нам, що більш швидкий потік над верхньою поверхнею дасть менший тиск, ніж повільніший потік по нижній поверхні, і цей перепад тиску призведе до підйому. Якщо ми подивимось на потік у точці на деякій відстані за переднім краєм аеропрофілю, ми виявимо, що ми могли б представити його дещо, як показано на малюнку нижче, з великим вектором швидкості на вершині аеропрофілю та меншим на дні.

Іншим способом представлення цього ж потоку було б поєднання «рівномірного» потоку та кругового потоку, таким чином, щоб швидкості додавалися зверху крила і віднімали знизу, як показано нижче.

Якщо можна сказати, що ці два потоки в кінцевому підсумку дають однаковий результат, потік, показаний на малюнку 3.2, можна сказати, є способом моделювання потоку навколо повітряного профілю. Насправді це працює дуже добре і є основною ідеєю того, як аеродинамік моделює потік навколо аеродинамічного профілю.

Ми могли б подивитися на верхню і нижню швидкості поверхні в декількох точках уздовж хорди і виявити, що в будь-якій точці ми можемо змоделювати цей місцевий потік «рівномірним» потоком і круговим типом потоку, як показано на малюнку 3.3.

У цій моделі «рівномірні» потоки на верхній і нижній поверхні були б точно такими ж, як швидкість вгору за течією або «вільним потоком», V _∞. Єдине, що зміниться в кожному положенні уздовж лінії хорди, - це потік кругового типу, який стане більш потужним, коли різниця швидкостей між верхньою та нижньою поверхнями стає все більшою і меншою, оскільки вона стає меншою.

Ці «кругові» потоки відомі як вихори (єдиний круговий потік - це вихор), і вони є математичним еквівалентом маленького торнадо. Виявляється, вихори є дуже важливими потоками в аеродинаміці і вони відбуваються фізично в багатьох місцях. Звичайно, немає вихорів посередині крила. Тут ми просто використовуємо реальний фізичний потік, вихор, щоб створити математичну модель, яка дає нам результат, який, як ми знаємо, насправді існує.

Ці чисто кругові потоки або вихори можна описати математично з точки зору їх циркуляції. Циркуляція технічно пов'язана з інтеграцією швидкості навколо замкнутого шляху, поняття, в яке нам не потрібно заглиблюватися тут, і йому дається символ гамма [γ або γ]. Нижня форма грецької літери γ використовується, коли ми поєднуємо ефекти безлічі малих вихорів, а форма верхнього регістру, γ, використовується або тоді, коли є лише один вихор, або коли ми дивимося на комбінований ефект безлічі малих вихорів. Циркуляція, гамма, по суті є вимірюванням швидкості обертання обертального потоку в вихорі, і її іноді називають силою вихору.

Отже, основна концепція тут полягає в тому, що для отримання підйомного потоку (більша швидкість зверху і менша швидкість на дні) ми поєднуємо вихровий потік з рівномірним потоком. Якщо ми зробимо це і математично проаналізуємо результат, ми знайдемо дуже важливу і дуже просту залежність між виробленим підйомником та циркуляцією та швидкістю вільного потоку, яка говорить:

Підйом = ρ V _∞ γ

Підйом дорівнює щільності потоку, що разів перевищує швидкість вільного потоку, що перевищує циркуляцію. Ви можете знайти добре зроблене виведення цього основного принципу в будь-якому хорошому підручнику з аеродинаміки, і там ви також виявите, що ця концепція настільки важлива, що їй дано ім'я Теорема Кутта-Йоуковського.

Як завжди, слід дивитися на агрегати, що беруть участь з цим параметром, тираж. Ми повинні мати на увазі, що ми розглядали цю концепцію потоку кругового типу як спосіб подивитися на підйомник на двовимірному зріз крила, секції аеропрофілю. Таким чином, ліфт, про який ми говоримо, - це підйом на одиницю прольоту крила; тобто, підйом на фут або підйом на метр. Знаючи це, ми можемо побачити, якими повинні бути одиниці гамми.

Підйом (фунтів на фут) = щільність (слимаки на фут в кубі) х швидкість (фути в секунду) х гамма

Прирівнювання одиниць у цьому співвідношенні говорить нам про те, що одиниці для гами повинні бути:

(фунт/фут) ÷ [(sl/ft ³) (ft/sec)] = (фунт футів сек) /сл

і знаючи, що F = ma; тобто 1 lb = 1 sl ft/sec ², ми знайдемо одиниці для гамма бути

одиниці для γ = фут ²/сек.

Ми можемо знайти ці одиниці трохи дивними. Вони не є ні одиницями для швидкості, ні прискорення. Однак це нормально, тому що циркуляція - це не швидкість або прискорення, це циркуляція!

Отже, що ж нам робити з цим? Якби це був суворий курс аеродинаміки або текст, ми б взяли кілька тисяч цих маленьких торнадо (вихорів) і поклали їх поруч уздовж лінії хорди або розвалу нашої секції аеродинаміки і зробити складний розрахунок, щоб точно побачити, яке значення гами кожен повинен мати, щоб дати правильний підйом для аерофольги заданої форми під заданим кутом нападу на вільний потік потоку потоку. Ми б засновувати це на формі, яку ми хотіли, щоб наша лінія розвалу аеродрому. Нарешті, ми б склали або «інтегрували» комбіновані циркуляції (гамми) для всіх наших маленьких вихорів і знайшли загальний підйом на аеродромі.

Ми також подивимося на «розподіл» цих циркуляцій або вихрових сильних сторін і знайдемо те, що ми могли б назвати їх «центроїдом» вихору; тобто місце на аерофользі хорди, де можна сказати, що загальний підйом діє, якби всі маленькі вихори можна було б замінити одним великим вихором. Ми б назвали це місце «центром ліфта».

Якщо ми все це зробили (і, знову ж таки, ми можемо знайти цю похідну в повній красі в будь-якому хорошому тексті аеродинаміки), ми знайдемо кілька цікавих і дуже корисних результатів, які ми перерахуємо нижче:

Для «симетричного» аерозолю (без розвалу)

• «Центр підйому» знаходиться на «чверті хорди»; тобто одна четверта відстані по лінії хорди від переднього краю.
• Двовимірний коефіцієнт підйому становитиме C _L = 2πα, де α - кут атаки (кут між лінією хорди і вектором швидкості вільного потоку).

Для криволінійного аерозольного профілю (несиметричний)

• «Центр підйому» знаходиться не у чверті хорди і він, по суті, рухається в міру зміни кута атаки.
• Двовимірний коефіцієнт підйому тепер буде C _L = 2 π (α - α _L0), де α _L0 називається «нульовим кутом підйому атаки» і є негативним кутом для позитивно вигнутий аеродром. Це означає, що крива підйому зміщується вліво, коли розвал збільшується, і що при заданому куті атаки вигнутий аерофольг буде виробляти більший коефіцієнт підйому, ніж симетричний аеродром (за умови, що аерокрил знаходиться під кутом атаки нижче, що для стійла).

Ми говорили про ці самі результати в першій главі, не кажучи багато про їх походження. Цей зсув кривої підйому та збільшення коефіцієнта підйому зі збільшенням розвалу є основою для використання стулок як тимчасового способу збільшення коефіцієнта підйому, коли необхідний приріст підйомної здатності, наприклад, на посадці.

Аеродинамічна теорія, яка б передбачила все це, називається «теорією тонкого аеропрофілю», і вона робить це точно так, як описано вище, припускаючи, що тисячі крихітних вихорів прокладені пліч-о-пліч у тому, що називається вихровим листом вздовж лінії розвалу аеропрофілю. Знаючи математичний опис форми потрібної лінії розвалу, швидкості вільного потоку та кута атаки, і вимагаючи, щоб через лінію розвалу не було потоку і щоб потік не йшов з однієї поверхні на іншу навколо заднього краю, теорія тонкого аеропрофілю може сказати необхідне розподіл циркуляції по лінії розвалу від передньої кромки до задньої кромки, щоб дати імітацію реального потоку навколо аеродрому.

Цей метод не може передбачити стійло. Для цього нам потрібно буде розглянути наслідки зсуву або в'язкості в потоці, і це вимагатиме від нас подивитися на «прикордонний шар» або область в'язкого потоку навколо фактичної поверхні крила. Це теж далеко за рамки матеріалу, який ми хочемо дослідити в цьому тексті.

Отже, чи існує простий спосіб передбачити наслідки розвалу, не вдаючись до теорії тонкого аеропрофілю якоїсь однаково безладної процедури? Виявляється, існує метод «задньої частини конверта» під назвою «Наближення Вайссінгера»

3.2 Наближення Вайсінгера

Апроксимація Вайсенгера базується на симетричних результатах теорії тонкого аерофольгу, які були перераховані в розділі вище. Ці результати говорять про те, що для симетричного аеропрофілю (по суті плоскої пластини) підйомник діє на чверть хорди, а коефіцієнт підйому в 2-пі разів перевищує кут атаки.

У нас також є теорема Кутта-Йоуковського, яка говорить, що підйом дорівнює щільності потоку, помноженій на циркуляцію та швидкість вільного потоку.

Тому ми можемо об'єднати ці два результати, сказавши, що ми можемо моделювати підйом на плоскій пластині, розмістивши один вихор на чверті хорди плоскої пластини (оскільки саме тут теорія говорить, що діє чистий підйом). Все це дає нам картинку, показану нижче.

В основному, ми збираємося об'єднати ці дві ідеї, які описують підйом, вибравши місце, де ми б наклали умову відсутності потоку через плоску пластину, яка буде прирівняти підйом з двох теоретичних результатів. Для цього нам потрібно щось знати про вихор, який ми раніше не вводили. Тобто швидкість, знайдена в або введена вихором на різних відстанях від його центру. Аеродинамічна теорія скаже нам, що кругова або тангенціальна швидкість у вихорі змінюється обернено своїм радіусом і є функцією циркуляції, γ, у вихорі. Теоретично вихор має нескінченну окружну швидкість у своєму центрі, і ця швидкість стає меншою, коли ми рухаємось далі від центру. Це дасть

V _{вихровий} = γ/(2πr)

Використовуючи це визначення окружної швидкості у вихорі, в галузі аеродинаміки прийнято визначати позитивний напрямок для γ за годинниковою стрілкою. Це кидає виклик звичайній математичній практиці, і слід дотримуватися обережності, щоб бути послідовним у використанні конвенції.

Це проілюстровано нижче.

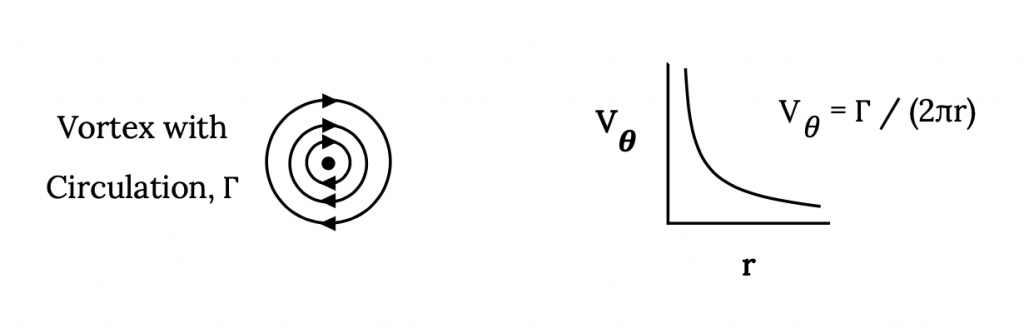
Повертаючись до нашої комбінації результатів теорії тонкого аеродрому та теореми Кутта-Йоуковського, ми маємо наступне завдання. Ми хочемо знайти якусь точку на плоскій пластині, де вихор, який ми розмістили на чверті хорди, дасть тільки потрібну кількість швидкості, щоб протидіяти складовій швидкості вільного потоку, нормальної для пластини, таким чином, що наші два погляди на коефіцієнт підйому або підйому дасть однакові відповіді. Одна теорія, теорема Кутта-Йоуковського говорить нам, що L = ρ V _∞ γ, а інша говорить нам, що коефіцієнт підйому C _L = 2πα.

Розуміючи, що підйом на двомірній плоскій пластині дорівнює коефіцієнту підйому, що разів перевищує динамічний тиск, помножене на довжину пластини («одновимірна площа»), можна записати:

L = ρ V _∞ γ = (2 πα) (½ ρ V _∞ ²) (с),

де «c» - хорда (довжина) плоскої пластини.

Легко помітити, що тут шукають зв'язок між кутом атаки та циркуляцією у вихорі. Ми пов'язуємо фізичну реальність збільшення підйому з кутом атаки з математичною моделлю, яка говорить, що ліфт збільшується з циркуляцією.

γ = πα V _∞ с.

Саме цей зв'язок ми використовуємо для створення нашої «задньої частини моделі конверта» під назвою Наближення Вайссінгера. Щоб побачити це, нам потрібно знову подивитися на нашу плоску пластину з вихором на чверті хорди і запитати себе, на якому радіусі від вихору буде швидкість від вихору достатньо, щоб збалансувати нормальну складову швидкості вільного потоку.

Якщо ми подивимось на цю ілюстрацію та використаємо останнє рівняння вище, щоб визначити циркуляцію, γ, з точки зору швидкості вільного потоку та кута атаки, а потім прирівняти швидкість від вихору та нормальну складову швидкості вільного потоку, ми знаходимо

V _θ = γ/(2πr) = (πα V _∞ с)/(2πr) = V _{∞ n} = V _∞ син (α) ≈ V ∞ α

або,

(α V _∞ c)/(2r) = V _∞ α, для малих кутів атаки.

Кінцевим результатом цього є те, що відстань, r, на якій ми повинні вирішити «відсутність потоку через плоску пластину», щоб зробити дві теоретичні моделі сумісними:

r = с/ 2.

Ми повинні вирішити для відсутності потоку через пластину в точці три чверті шляху назад (в точці три чверті хорди), щоб зробити це «наближення» працювати. Називаємо цю точку «контрольною точкою».

Гаразд, так в чому ж велика справа? Ми знайшли новий спосіб отримати результат, який ми вже знаємо, і це тільки для плоскої тарілки! Як це «наближення» може сказати нам все, що ми ще не знаємо?

Причина, по якій це так корисно, полягає в тому, що ми можемо «побудувати» приблизні моделі кулачкових або закритих аерозолів з плоских пластин. Розглянемо простий випадок симетричного аерофольгу з однотонним клапаном, що займає кінцеві 20% його хорди. Ми можемо змоделювати це як дві послідовні плоскі пластини з однією плоскою пластиною довжиною 80% хорди аеропрофілю та іншими 20% хорди, і ми можемо відхилити «заслінку» і подивитися, що він робить з коефіцієнтом підйому. Те, як це робиться, проілюстровано на малюнку нижче:

У наведеному вище випадку ми закінчимо двома рівняннями та двома невідомими, двома значеннями циркуляції. Щоб отримати ці два рівняння, ми дивимося на потоки, нормальні для двох пластин у відповідних «контрольних точках», які були розміщені в точках ¾ хорди на кожній пластині або панелі. Давайте подивимося спочатку на контрольну точку на першій панелі.

У цій точці повинні бути враховані три швидкості; складова швидкості вільного потоку, нормальна для панелі, швидкість, індукована вихором на першій панелі, і швидкість, індукована вихором на другій панелі. На малюнку нижче ми бачимо, що швидкість вільного потоку спрямована вгору, тоді як швидкості від двох вихорів будуть в протилежних напрямках (що завдяки першому вихору «вниз», а швидкість від другого вихору - «вгору», якщо припустити, що вихори «позитивні» або за годинниковою стрілкою). Ми можемо враховувати ці напрямки або розумовою бухгалтерією і зазначивши, що всі вони повинні додавати до нуля, або сумлінно враховуючи знаки на векторних величинях, відзначаючи, що радіуси (r ₁₁ і r ₂₁) мають знаки, пов'язані з їх напрямком.

Зверніть увагу, що швидкість, індукована в контрольній точці 1 вихором на панелі 2, не зовсім перпендикулярна панелі 1. Ми могли б бути дуже точними і використовувати трохи тригонометрії, щоб з'ясувати точний кут і врахувати його, щоб знайти справжній нормальний компонент, або ми могли б просто припустити, що він досить близький до нормального, щоб ігнорувати кут. Оскільки це приблизний метод у будь-якому випадку, за винятком дуже великих кутів (скажімо, десять градусів або більше), ми зазвичай ігноруємо помилку. Роблячи це, ми можемо написати рівняння, додавши дві вихрові складові швидкості та прирівнюючи їх суму до складової вільного потоку.

В ₁₁ + В ₂₁ = V _{∞ 1} = V _∞ грін (α ₁ ) ≈ V _∞ α ₁

де

V ₁₁ = γ ₁/(2πr ₁₁)

V ₂₁ = γ/(2πr ₂₁)

і де

р ₁₁ = 0,4с

р ₂₁ ≈ — 0,25 см

Тепер ми б зробили точно те ж саме в контрольній точці на другій панелі.

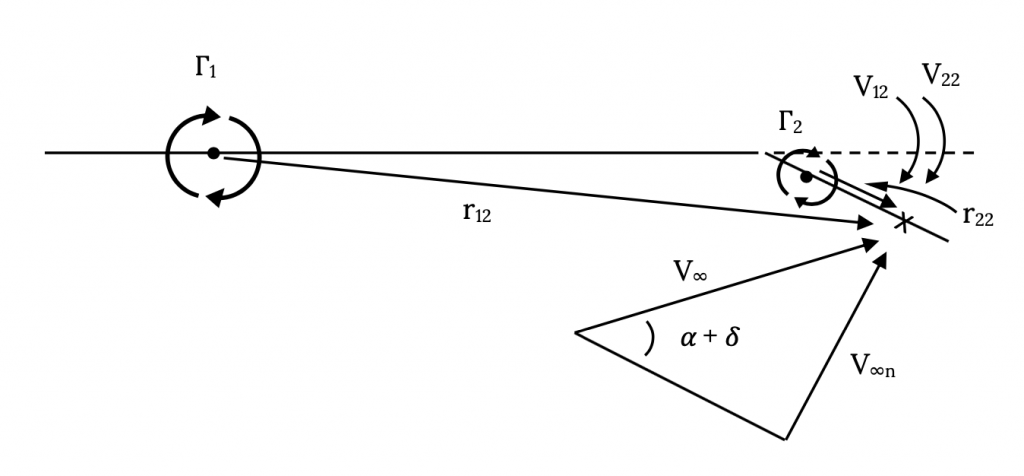
Тут наше рівняння буде схоже на рівняння в контрольній точці на панелі, за винятком того, що нам, ймовірно, доведеться враховувати той факт, що кут відхилення заслінки, ймовірно, буде занадто великим, щоб просто ігнорувати при знаходженні нормальної складової швидкості вільного потоку.

V ₁₂ + В ₂₂ = V _{∞ н2} = V _∞ грін (α ₂) = V _∞ гріх (α + δ)

де

δ = кут відхилення заслінки

V ₁₂ = γ ₁/(2πr ₁₂)

V ₂₂ = γ ₂/(2πr ₂₂)

р ₁₂ ≈ 0,75см

р ₂₂ = 0.1c

Тоді ми б одночасно вирішували ці два рівняння, кожне з яких має два невідомі (γ ₁ та γ ₂) для цих невідомих значень. Потім ми використали б ці два значення циркуляції, щоб знайти загальний коефіцієнт підйому та підйому, де підйомник просто буде знайдений з теореми Кутта-Йоуковського, підсумовуючи підйомники на кожній панелі.

Л = Σ ρ V _∞ γ = ρV _∞ [γ ₁ + γ ₂]

і коефіцієнт підйому буде

С _Л = Л/(½ ρ В _∞ ² с) = 2 [γ ₁ + γ ₂]/(В _∞ c)

Вправа:

Вирішіть проблему вище для швидкості вільного потоку 100 миль/год, відхилення щитка 20 градусів і 5-футової хорди крила в умовах рівня моря під кутом атаки 5 градусів. Як цей коефіцієнт підйому порівнюється з тим, що для симетричного аерокрила під однаковим кутом атаки?

Зверніть увагу, що у наведеному вище приблизному рішенні для закритого, симетричного аеропрофілю ми маємо дуже грубе «розподіл підйому» над аерофолистом хорди, тобто ми знаємо, як підйом можна розділити, щоб діяти в двох місцях вище. Якби ми вирішили це для декількох різних кутів атаки, ми виявимо, що відносні значення двох вихрових сил (циркуляцій) зміняться. Якби ми уважно подивилися на це, ми виявимо, що, на відміну від симетричного аеродрому, де підйомник завжди можна сказати, що він діє на аерофользі чверть хорди, для вигнутого аеродрому точка, де буде діяти підйомник (центр підйому або центр тиску) буде рухатися з кутом атаки і буде виконувати функцію розвалу. Якби ми хотіли знайти це точніше, ми могли б використовувати більше панелей та більше вихорів та контрольних точок (разом із більшою кількістю рівнянь). Для наведеного вище прикладу може бути природним просто розділити аеропрофіль на п'ять панелей однакової довжини, кожна 20% від вихідного акорду, виглядаючи приблизно на зразок ескізу нижче.

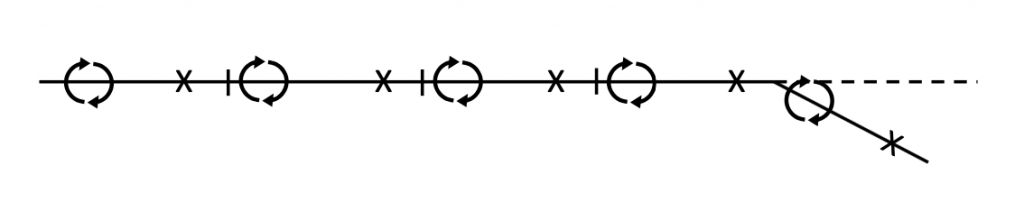
І, це не дуже важко уявити, щоб розширити цей метод до по-справжньому вигнутого аеропрофілю, як показано на малюнку 3.12.

Це просте наближення, засноване на результатах аеродинамічної поведінки плоских пластин, таким чином, було розтягнуто в справжнє «числове рішення» для аеродинамічного профілю будь-якої форми розвалу з такою кількістю панелей, скільки ми хочемо використовувати. Ми можемо використовувати його, щоб знайти загальний коефіцієнт підйому або підйому для аеропрофілю з будь-якою формою розвалу, а також знайти спосіб розподілу підйомника по аерофолисту хорди.

Інша річ, яку ми можемо знайти з цього, - це «момент качки» аерофольги, його схильність обертати носом вгору або носом вниз про будь-яку бажану опорну точку на хорді. Момент качки просто знаходять, приймаючи кожну «підйомну» силу, знайдену з окремих циркуляцій, і множивши її на відстань або «моментну руку» між цим вихором та бажаною контрольною точкою. Якщо, наприклад, ми хочемо використовувати передню кромку крила в якості нашого опорного моменту (загальний вибір у теоретичних або числових розрахунках), нам потрібно лише взяти кожне значення гамми, що разів перевищує відстань від переднього краю аерокрила та цього вихору та підсумувати їх, щоб отримати загальний момент качки про провідний край.

Для симетричного аеропрофілю (плоска пластина), де центр підйому завжди знаходиться на чверті хорди, цей момент качки навколо переднього краю завжди буде підйомом, помноженим на відстань чверті хорди. Коефіцієнтом моменту пітчингу для цього випадку буде підйомник, помножений на відстань чверті хорди, розділений на динамічний тиск, що помножений на квадрат хорди. Зробіть швидкий розрахунок, щоб побачити, що це буде?

3.3 Момент пітчингу

Поки ми говоримо про пошук моменту пітчингу, давайте подивимося на деякі особливі випадки. Момент пітчингу можна обчислити або виміряти щодо будь-якої точки, яку ми хочемо використовувати. Часто в аналітичних або числових розрахунках зручно знаходити момент качки навколо передньої кромки крила. З іншого боку, при тестуванні аеродинамічної труби може бути зручніше виміряти момент в якийсь момент від 20% до 50% назад від переднього краю через простоту приєднання системи балансу сили та моменту там.

У першій главі ми згадали два значущих місця, де момент пітчингу або його коефіцієнт має особливе значення. Це були центр тиску (центр підйому) та аеродинамічний центр; точки, де коефіцієнт моменту дорівнює нулю або де він залишається постійним у міру зміни коефіцієнта підйому та кута атаки. Відповідно до теорії тонкого аерофольгу вони збігаються на чверті хорди для симетричного аеропрофілю, але для вигнутого аеропрофілю центр тиску зазвичай рухатиметься, коли кут атаки змінюється, тоді як аеродинамічний центр залишається на чверті хорди. Ми можемо переконатися, що цей теоретичний результат досить добре відповідає реальності, подивившись на аеродинамічні графіки даних, представлені в Додатку А (розглянуто раніше в главі 1). Часто на цих графіках представлені два графіки для коефіцієнта качінг-моменту з першим (зліва в більшості цифр) ділянкою C _Mc/4 (коефіцієнт моменту на чверті хорди) та іншим графіком (зазвичай праворуч) C _MAC (коефіцієнт моменту в аеродинамічному центрі). На сюжетах в Додатку А для викривлених аерозольних профілів видно, що C _Mc/4 є ненульовим за значенням і змінюється з кутом атаки, тоді як C _MAC відносно постійний до настання стійла. На ділянках симетричних даних аеропрофілю обидві ці величини є нульовим (або близьким нулем) за значенням і постійними до зупинки. У стійлі підйом або розподіл тиску над аерофолистом різко змінюється, оскільки потік починає відокремлюватися над поступово більшими частинами аеродрому, а наближення теорії тонкого аерофольгу далекі від дійсності.

Як зазначалося в попередньому розділі, коефіцієнт пітчинг-моменту і моменту можуть бути розраховані разом з підйомом при використанні наближення Вайсінгера. Щоб знайти місце розташування центру тиску, нам потрібно лише використовувати визначення цієї точки як буття, де момент дорівнює нулю, щоб знайти її місце розташування. Виходячи з ілюстрації нижче, ми можемо припустити, що центр тиску розташований в деякій точці X _cp і підсумувати моменти про цю невідому точку через різні сили підйому, індукованих циркуляцією, рівним нулю.

ρ V _∞ [γ ₁ (х ₁ -х _сп) + γ ₂ (х ₂ -х _сп) + • • • • + γ _n (х _п -х _сп)] = 0

У цьому рівнянні x ₁, x ₂, через x _n - місця уздовж хорди різних вихорів (кожен у чверті хорди своєї панелі), а x _cp - невідоме розташування центру тиску. Це вирішується для _{х ср}, розташування центру тиску. Зверніть увагу, що для симетричного аерофольгу (плоскої пластини) це положення не повинно змінюватися з кутом атаки, тоді як для вигнутого аерофольгу x _cp буде різним для кожного кута атаки.

Подібним, але трохи складнішим способом ми могли знайти розташування аеродинамічного центру з результатів підйому Weissinger Aprosimation. Це передбачало б знаходження точки, де dC _M /DC _L = 0. Ми залишимо цей розрахунок для тексту або курсу з аеродинаміки.

3.4 Крила (3-D аеродинаміка)

Як було зазначено в першій главі, основною відмінністю між двовимірним потоком навколо аеропрофілю та тривимірним потоком навколо крила є потік навколо кінчика крила від низу до верху крила. Це призводить до кількох речей:

• Вихідний потік по нижній частині крила біля кінчика.
• Потік всередину по верхівці крила біля кінчика.
• Причіпна вихрова система.
• «Зниз» на крилі, викликаний задньою вихровою системою.
• «Індукований опір», спричинений змивом.

Цей вихровий потік з кожного кінчика крила є цілком реальним потоком, який можна побачити в аеродинамічній трубі або з димом, або просто встромляючи струну в потоці за кінчиком крила. Це також можна побачити на літаках в польоті, коли атмосферні умови правильні. Якщо в повітрі є достатня кількість вологи у вигляді високої відносної вологості або через водяну пару у вихлопі реактивного двигуна, що втягується в причіпні вихори, низький тиск у вихровому ядрі призведе до конденсації водяної пари, роблячи його видимим як пара «білих торнадо», що тягнеться за кожним наконечник крила. Цікаво спостерігати за ними, коли їх видно з високо літаючих струменів і бачити, як довго вони зберігаються. Вони можуть існувати протягом багатьох миль позаду генеруючого літака, ілюструючи як кількість енергії в вихорі, так і небезпеку для інших літаків, які можуть зіткнутися з ними.

Ці «задні вихори» є ключовим фактором у спробі створити будь-яку математичну модель 3-D потоку навколо і за реальним крилом. По суті, це робиться шляхом згинання вихорів, які використовувалися для моделювання потоку над аерофолистом під кутом 90 градусів і дозволяючи їм слідувати за крилом. І, оскільки ми знаємо, що підйом на крилі змінюється вздовж його прольоту і не просто залишається однаковим до кінця крила, ми дозволяємо вихори повертати праворуч або ліворуч і відірватися від крила по всьому прольоту. Це виробляє те, що називається «підковоподібна вихрова система».

Хоча цей теоретичний висновок виходить за рамки передбачуваного матеріалу, його суть полягає в наступних фактах або припущеннях:

• Загальний тираж на крилі передбачається змінюватися по прольоту і йти до нуля на кінчиках крила.
• «Задні вихори» викликають низхідний потік або «вниз», що створює невелику, але значну швидкість вниз на самому крилі. (Насправді, це спосіб врахувати низхідний імпульс потоку, який виникає в результаті підйомної сили. Це також можна знайти з рівняння імпульсу, якби ми мали достатню інформацію.)
• Так само, як взаємодія швидкості вільного потоку, V _∞, з вихровими циркуляціями на крилі призводить до підйому (теорема Кутта-Йоуковського), взаємодія цієї швидкості «вниз» з вихровими циркуляціями викликає опір. Ми називаємо це «індукованим перетягуванням».

Використовуючи цю підкову модель вихору і припускаючи, що всі вихори на крилі об'єднані в одне, схоже на мотузку, ядро на чверті хорди крила, а також припускаючи, що хорда чверті крила не змітається, метод, який називається «теорією підйомної лінії», може бути використаний для пошуку зміна ліфта вздовж прольоту і індукований опір для будь-якого нерозгорнутого крила помірного до високого співвідношення сторін. Будь-який хороший текст по аеродинаміці матиме повноцінний розвиток такого підходу до 3-D аеродинаміки і представить його результати.

Одним з результатів використання теорії підйому лінії буде «оптимальний» випадок, тобто розподіл підйому на крилі, де індукований опір є мінімальним. Це виявляється рішенням, де розподіл циркуляції по крилу має еліптичну форму та математичну форму. Це спеціальне рішення дасть рівняння для індукованого коефіцієнта опору, яке ми вже цитували в першій главі,

С _Ді = С _Л ²/(πар)

де «AR» - співвідношення сторін,

АР = б ² /с = б/с _{середнє}.

Більш загальна (неоптимальна) форма цього рівняння для індукованого коефіцієнта опору включає ще один термін, «e», відомий як коефіцієнт ефективності Освальда, який враховує нееліптичні променеві варіації циркуляції.

С _Ді = С _Л ²/(π АР е)

Цей коефіцієнт корисної дії Освальда можна обчислити з теорії підйомних ліній у вигляді ряду Фур'є.

Хоча це не мета цього тексту, щоб вдаватися в багато деталей, вивчаючи теорію підйому лінії, я хотів би коротко подивитися на те, що він говорить про ліфт для спеціального, мінімального опору, випадку еліптичного розподілу ліфта, тому що ми часто використовуємо цей особливий випадок, щоб взяти перший погляд на вплив крила проектування з аеродинаміки і продуктивності. Не виводячи їх, ми просто розглянемо деякі найважливіші результати теорії підйомних ліній, пов'язаних з підйомом:

Л = (π/ 4) ρ V _∞ Bγ _центр

де

b = розмах крила

γ _center = величина циркуляції в центрі прольоту крила

і

γ _центр = (2C _L V _∞ S)/(πb)

Зверніть увагу, що це робить коефіцієнт підйому функцією співвідношення сторін:

С _Л = Л/(½ ρ V _∞ ² S) = (π Bγ _центр)/(2V _∞ S) = (π АР γ _центр)/(2bV _∞)

Це говорить про те, що для будь-якого заданого кута атаки (або значення циркуляції, оскільки γ _центр повинен збільшуватися з кутом атаки) більш високий коефіцієнт співвідношення сторін крила дасть більш високий коефіцієнт підйому, ніж низький крило AR.

Якщо ми побудуємо коефіцієнт підйому проти кута атаки для двох крил з різним співвідношенням сторін, ми виявимо, що «нахил» кривої підйому зменшиться зі зменшенням співвідношення сторін. Максимальне значення нахилу - 2-пі, двовимірне значення аерокрила, еквівалентне нескінченному співвідношенню сторін крила.

Інший спосіб подивитися на цей же ефект - подивитися на кут атаки, при якому повинні бути пролетіли два крила різного співвідношення сторін, щоб отримати однакове значення коефіцієнта підйому:

α ₂ = α ₁ + (С _Л/π) [(1/АР ₂) — (1/АР ₁)]

Наведені вище відносини дають нам цінні інструменти для вивчення впливу конструктивних змінних, таких як співвідношення сторін крила на аеродинаміку і продуктивність літака. Якщо ми хочемо використовувати помірне співвідношення сторін крило замість дизайну з високим співвідношенням сторін для, скажімо, структурних причин або для поліпшення динаміки рулону, ми можемо побачити, який штраф ми заплатимо. Часто штраф може бути не таким великим, як ми могли б спочатку вважати, виходячи з наших базових знань, що високе співвідношення сторін, як правило, бажано.

Ці рівняння, як уже згадувалося раніше, для ідеального випадку, еліптичний розподіл підйому або мінімальний індукований випадок опору. Тим не менш, вони можуть дати нам досить гарне уявлення про те, як такі речі, як зміни співвідношення сторін, впливатимуть на продуктивність будь-якого тривимірного крила.

Одне останнє, що я хотів би згадати в цьому розділі, стосується припущень, згаданих раніше для теорії підйому лінії. Було відзначено, що дана теорія передбачає, що чверть хорда крила неохайна. Ще одне припущення, притаманне використанню теорії підйомної лінії, яка не згадувалася, полягає в тому, що теорія не дуже хороша для крил з низьким співвідношенням сторін. Навіть з цими двома важливими обмеженнями, теорія підйому лінії дає нам деякі важливі уявлення про 3-D аеродинаміку. Але що б ми зробили, якщо ми дивимося на крило з розгорткою або низьким співвідношенням сторін?

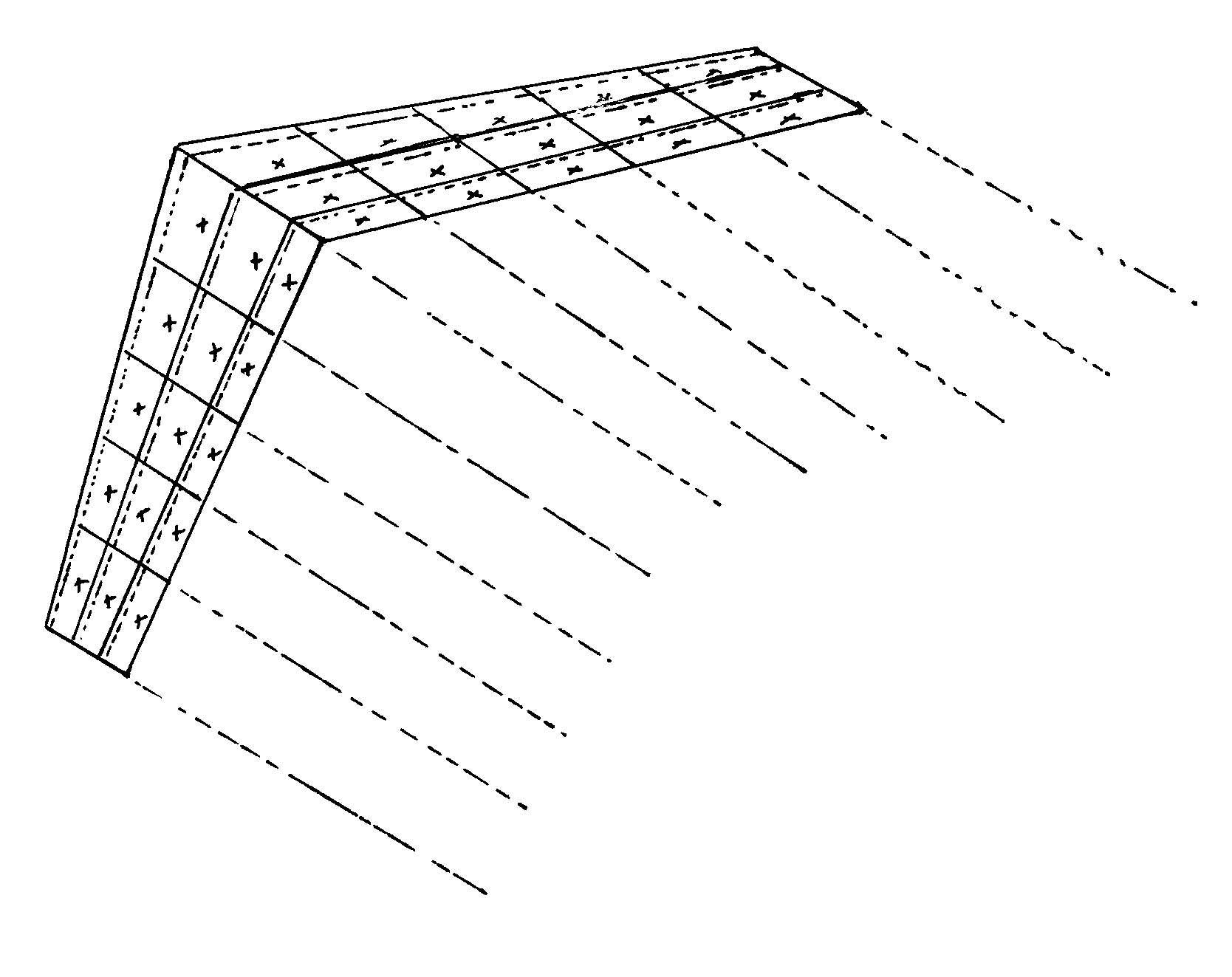
Для підміталих крил, крил з низьким співвідношенням сторін або будь-якого іншого крила за межами припущень теорії підйому лінії звичайним підходом є перехід до деякої варіації того, що називається теорії «вихрової решітки». Крило (або навіть весь літак) розділене на панелі і єдиний «підковоподібний» вихор розміщений на чверті хорди кожної панелі в тому, що по суті є тривимірною версією наближення Вайссінгера. Якщо крило розбито на N панелей, існує N підковових вихорів, і вони повинні бути вирішені шляхом встановлення N рівнянь. Рівняння розв'язуються за умови відсутності протікання через панелі (та ж ідея, що і при наближенні Вайсінгера) на центральному прольоті тричвертної хорди панелі. Це рішення втричі складніше, ніж метод 2-D Вайссінгера, оскільки кожен підкововий вихор має три сегменти (один охоплює чверть хорди панелі, а два інших діють як «кінцеві вихори» від першого вихору на краях панелі. Так само, як і в двовимірному методі, рівняння, розв'язані в «контрольних точках», повинні були враховувати всі швидкості, індуковані всіма вихорами на аеродромі, а також швидкість вільного потоку, у 3-D вихровій решітці рівняння в контрольній точці кожної панелі має враховувати швидкості, індуковані всіма три вихрові сегменти з усіх N панелей, а також для швидкості вільного потоку.

Методи вихрової решітки спочатку можуть бути залякуючими; однак, як і наближення Вайссінгера у 2-D, вони просто використовують N рівнянь для вирішення для N невідомих, де невідомим є сила підковоподібного вихору на кожній 3-D панелі. Все інше зводиться до моделювання геометрії 3-D крила. Результатом буде 3-D вектор швидкості, паралельний кожній контрольній точці панелі, і вони можуть бути використані для пошуку тиску, сил і моментів навколо крила.

3.5 Вихрова аеродинаміка: Вінглети

Ми розглянемо один остаточний предмет у цій главі - «вихрова аеродинаміка». Як ми вже бачили, вихори відіграють головну роль у тому, як ми математично моделюємо аеродинаміку аеродинаміки та крила. І, як ми бачили у випадку тривимірних потоків навколо кінчиків крила, вихори насправді відіграють дуже реальну роль у створенні таких речей, як підйом та перетягування, а математичні моделі, які ми будуємо для пояснення аеродинаміки, також чудово справляються з моделюванням цих реальних вихорів та їх ефектів.

Існує багато ситуацій, крім вихорів наконечника крила, де ці торнадо подібні потоки існують в «реальному житті» і відіграють головну роль у створенні сил і моментів на літаках і крилах. Однією з завдань аеродинаміка є правильне моделювання цих вихорів та їх ефектів, а інша робота може полягати у визначенні, чи є способи використовувати ці закручені потоки на нашу користь способами, що покращить аеродинаміку та продуктивність польоту літака.

Ми розглянемо два дуже важливих і цікавих випадку, коли вихрова аеродинаміка грає важливу роль. Вони полягають у використанні «вінглетів» та «розширень передніх країв» (іноді відомих як «страки» або «рукавички крила»).

На даний момент крило є досить відомим доповненням до кінчиків крила багатьох літаків, але його призначення широко неправильно зрозуміла. Протягом багатьох, багатьох років інженери та вчені спробували багато підходів, які могли б зменшити силу або наслідки вихорів наконечника крила або що б усунути їх взагалі. На жаль, закони фізики важко подолати, і ця обертальна енергія, яку ми кількісно оцінюємо як «циркуляцію», повинна йти десь на вершині крила, і насправді немає ніякого способу усунути її в польоті, крім того, щоб дозволити їй повільно розсіюватися як кінцева вихрова пара десь в атмосфері далеко нижче за течією. літака. Ми можемо поставити великі пластини на кінчик крила або створити цікаві форми крила в спробах усунути або прискорити розсіювання задніх вихорів, але звичайний ефект полягає в тому, щоб просто створити дещо інший круговий розподіл тангенціальної швидкості всередині самого вихору, шаблон, який може або не може зробити вихори менш небезпечними для заднього літака і може призвести або не може призвести до будь-якого зменшення індукованого опору крила. Зазвичай ефекти таких «виправлень» більше в уяві їх винахідника, ніж в реальному житті.

Вінглет, більш відомий як крило Уіткомба після їх винахідника Річарда Уіткомба з NASA-Ленглі, всупереч загальноприйнятій мудрості, не призначений для усунення вихорів крила. Замість того, щоб намагатися усунути те, що неможливо усунути, не усуваючи підйом крила, Віткомб вирішив використовувати задні вихори для створення позитивного ефекту. У розмові з автором містер Віткомб пояснив, що він бачив, що вінглети працюють так само, як кіль на вітрильнику, який плаває або «прив'язується» до вітру. Кіль вітрильника - це своєрідне крило на дні човна, і коли вітрильник пливе на вітер, вперед сила зовсім не йде з вітрила. Натомість вітрило створює бокову силу, яка штовхає кіль через воду таким чином, щоб створити спрямовану вперед силу. Сила вперед штовхає вітрильник на вітер йде від маленького крила у воді, а не від великого крила, яке ми називаємо вітрилом.

Створюючи крило, Річард Віткомб міркував, що якщо велике крило на вітрильнику може створити потік над меншим крилом (кілем), який би створював тягу, повинен бути спосіб взяти потік, створений великим крилом на літаку (вихор наконечника), і використовувати його для створення тяги на меншому крилі. Це менше крило виявилося крильцем. Крило Whitcomb розміщується під тим, що здавалося б негативним кутом атаки на кінчик крила таким чином, що поєднання швидкості вільного потоку та швидкості потоку вихору крила створює «підйом» на крило, яке насправді спрямоване вперед, даючи тягу. І виходить, що ця тяга досить значна, щоб поліпшити відносини підйому-перетягування на крилі на п'ятнадцять-двадцять відсотків. Це може призвести до дуже значних поліпшень продуктивності польоту літака та економіки.

3.6 Вихрова аеродинаміка: Вихор переднього краю

Другий тип реального вихору, який ми хочемо розглянути дуже коротко, - це «вихровий передній край». Такий вихор утворюється, коли крило змітається на кути близько 50 градусів і більше. Ці вихори, проілюстровані на малюнку 3.18 нижче, є результатом поєднання тривимірного, променевого потоку на крилі та від нормального потоку навколо переднього краю крила. Цей комбінований потік фактично відокремлюється від поверхні крила на передньому краї, але, завдяки обертальному потоку у вихорі, знову прикріплюється до поверхні крила таким чином, що крило не затихає під звичайним кутом атаки п'ятнадцять-двадцять градусів, але має прикріплений потік і піднімається до набагато більших кутів атака.

Крила, як правило, змітаються, щоб затримати початок трансонічного опору біля Маха Першого і зменшити величину цього підйому опору. З іншого боку, підміталі крила виробляють менший звичайний підйом під заданим кутом атаки, ніж неохайне крило, майже так само, як крила нижчого співвідношення сторін дають менший підйом під заданим кутом атаки, ніж крила з високим співвідношенням сторін. Ефект вихору передньої кромки дворазовий. По-перше, зберігаючи потік, прикріплений до набагато вищих, ніж нормальні кути атаки, вони дозволяють крилу виробляти підйом при цих кутах, вищих за звичайні кути атаки. До цього збільшеного кута атаки перевагою є додатковий підйом, який називається «вихровим підйомом», який створюється дуже низьким тиском на вихровому ядрі. На жаль, цей низький тиск у вихорі також додає деякого опору, але чистий ефект може бути дуже корисним, дозволяючи літакам, які потребують високо розметаних крил, ефективно працювати на трансзвукових та надзвукових швидкостях, щоб все ще отримати потрібний їм підйомник на більш низьких дозвукових швидкостях. Вони також можуть дозволити військовим винищувачам «літати» при дуже незвичайних установках (кутах атаки), які можуть бути дуже корисними в боях повітря-повітря.

Іноді ми хочемо створити таку саму здатність на крилах, які не так сильно прокотилися. Це можна зробити, додавши сильно змітаються розширення переднього краю або облямівки. Ці страйки створюють власні вихори переднього краю, які продовжуються над крилом позаду них, даючи багато переваг, згаданих вище, і дозволяючи літакам з відносно низькою розгорткою крила літати під набагато вищими, ніж звичайні кути атаки, коли це необхідно. Один літак, який добре використовує цей ефект, - це F-18 ВМС. Його дуже довгі і сильно розметані страйки дозволяють йому працювати під високими кутами або атакою та низькими швидкостями, необхідними для посадки та зльоту на авіаносцях, а також надаючи йому дуже корисний високий кут маневреності атаки, що дуже корисно в винищувальному бою.

Як було згадано на початку цієї глави, висвітлення в розділі насправді не потрібно, щоб мати можливість зрозуміти або працювати з матеріалом про продуктивність літака, який буде слідувати. Він був включений просто, щоб заповнити деякі з пропусків, які могли бути залишені відкритими в першій главі. З іншого боку, він може бути використаний для підвищення наступного покриття продуктивності літака та для кращого співвідношення його з деякими основними поняттями в аеродинаміці.

Домашнє завдання 3

1. Airbus 380-100 призначений для круїзу на 35000 футів при кількості Маха 0,85. Його вага в круїзі становить приблизно один мільйон фунтів. Він має площу крила 9100 футів ² і розмах крила 262 фути. Припускаючи, що підйом дорівнює вазі, а тяга дорівнює опору і що в круїзі на цій висоті потрібно 50,000 фунтів тяги, знайдіть:

a. швидкість польоту в милі на годину і в вузлах

б. коефіцієнт підйому

c Коефіцієнт опору

d Його число Рейнольдса, засноване на середньому акорді

2. Якщо літак злітає, просто прискорюючись вниз по злітно-посадковій смузі, поки він не матиме достатньої швидкості для його підйому, щоб дорівнювати його вазі, а його крило знаходиться під кутом п'яти градусів атаки, які швидкості потрібні для зльоту на рівні моря і на 5000 відчувають висоту, припускаючи, що його крило має нахил кривої підйому (dC) _L/dα) 0,08 за градус і нульовий кут підйому атаки (α _L0) мінус один градус? Також знайдіть зазначену швидкість польоту на обох висотах. Припустимо, що літак важить 11,250 фунтів і має площу крила 150 футів ².

Примітка: Зазвичай більшість літаків прискорюються при низькому значенні коефіцієнта підйому, а потім «обертаються», щоб збільшити кут атаки до значення, яке дасть підйом+вага при визначеній швидкості зльоту. Це дозволило б злетіти на меншу відстань, ніж метод вище. Ми розглянемо це докладно пізніше в курсі.