2: Двигун

Last updated

Oct 25, 2022
Save as PDF
- 1: Вступ до аеродинаміки
- 3: Додаткові інструменти аеродинаміки

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Вступ

У главі 1 ми розглянули стандартну атмосферу, середовище, в якому працюють літальні апарати, рівняння Бернуллі та його зв'язок з аеродинамікою літака (або точніше крила), а також деякі основні параметри, що впливають на аеродинамічні показники літака. У цьому розділі ми розглянемо, як ми враховуємо рух літака; тобто реактивні або гвинтові двигуни. Це означає, що ми будемо дивитися на фактори, які впливають на такі речі, як тяга літака і потужність. Ми також виявимо, що ті самі фактори, що пояснюють тягу, також можуть бути використані для обліку деякого опору літака.

Дивлячись на тягу, потужність та тягу, ми зацікавлені в тому, як вони можуть змінюватися залежно від швидкості літака та висоти. Ми повинні мати базове розуміння цих залежностей, якщо ми хочемо врешті-решт використовувати їх у визначенні продуктивності літака.

Літак двигуни, звичайно, предмет цілих інженерних курсів, що займаються такими речами, як двигуни внутрішнього згоряння і повітряно-дихальні реактивні двигуни. Ми хочемо обмежитися дуже простим підходом до розуміння того, як працює двигун, не вдаючись у будь-які деталі, ніж це абсолютно необхідно. На щастя, ми зможемо це зробити.

2.1 Реактивні двигуни

Реактивні двигуни випускаються в широкому діапазоні конструкцій. Більшість вважаються «турбінними» двигунами тому, що турбіни використовуються для отримання енергії з високошвидкісного вихлопного потоку для приводу «компресора» для стиснення потоку в двигун до додавання палива і згоряння, але при дуже високих швидкостях (гіперзвуковий потік) можна отримати стиснення через ударні хвилі і нетурбінний реактивний двигун називається «прямоточним» є результатом. Однак ми збираємося обмежитися дозвуковим, нестисливим польотом, де завжди потрібні турбіни та компресори.

Найосновніший тип реактивного двигуна називається «турбореактивним», і він складається в основному з вхідного отвору, а потім компресора, який збільшує тиск (і знижує швидкість) повітря перед тим, як він потрапляє в камеру згоряння, де паливо додається і запалюється. Після згоряння турбіна витягує достатньо енергії з високоенергетичних (високошвидкісних) вихлопних продуктів для приводу компресора, а потік потім виходить через вихлоп двигуна на високій швидкості, щоб забезпечити тягу.

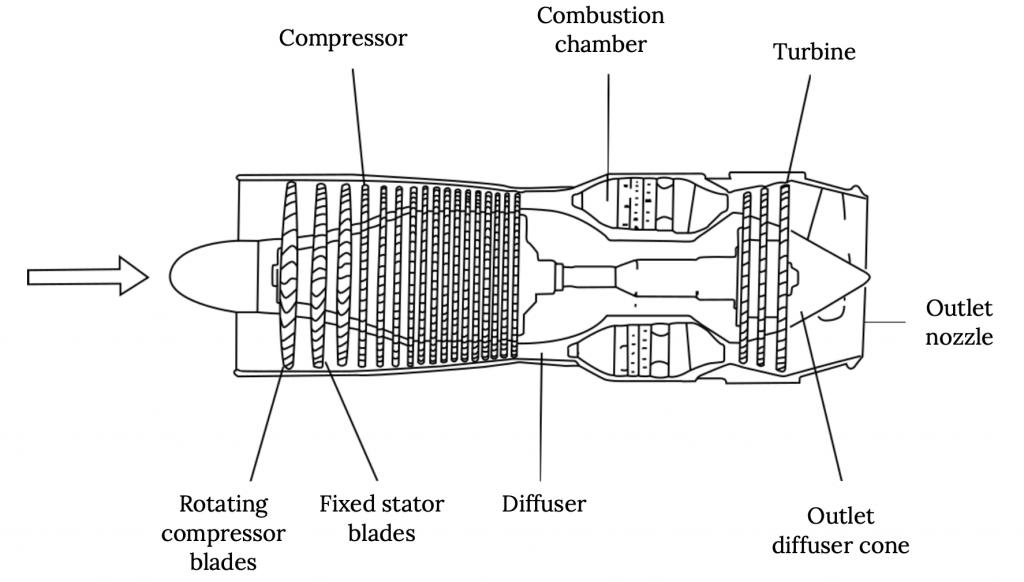
Поперечний переріз турбореактивного двигуна показує, як його змушують у все менші простори. Спочатку повітря надходить в двигун і проходить набір обертових лопатей компресора. Далі він переміщається в набір нерухомих лопатей статора відразу після цього, перш ніж продовжувати в іншу частину компресорної секції, яка постійно звужується. Потім повітря проходить через дифузор в камеру згоряння. Після камери згоряння вона проходить через турбіну, де їй дають розширюватися, а потім вихідний патрубок, повз вихідного конуса дифузора в центрі. — Малюнок 2.1: Ілюстрація турбореактивного двигуна

Виявляється, чистий турбореактивний не дуже ефективний спосіб зробити тягу. Це створює тягу через дуже високошвидкісний вихлоп, і це одночасно дуже шумно і дуже схильний до втрат. Високошвидкісний вихлопний струмінь по суті розриває свій шлях через навколишнє повітря, і ця жорстока взаємодія між вихлопом та атмосферою призводить до багатьох втрат, подібних до тертя, і робить багато шуму.

Ми розглянемо реактивний рух з точки зору зміни імпульсу (енергії в одиницю часу) з різницею між імпульсом у вихлопі і впускним отвором двигуна, що враховує тягу, і, на перший погляд, буде здаватися, що будь-який спосіб ми можемо отримати зміну імпульсу так само добре, як і будь-який інший спосіб, але це не той випадок.

Імпульс - це по суті маса, помножена на швидкість (швидкість). Це означає, що існує два способи отримати зміну імпульсу. Один - взяти невелику кількість маси і прискорити її до дуже високої швидкості, як це робиться в турбореактивному двигуні. Інший - взяти велику кількість маси і прискорити її на меншу кількість. Як з'ясовується, останній спосіб є найефективнішим способом отримання тяги. Це ніби як порівнювати ефекти великого стельового вентилятора, що повільно обертається, з ефектами маленького «особистого» вентилятора. Якщо ви зробили два повітряні човни з гвинтовим приводом типу, що використовуються на болотах, один човен з невеликим гвинтом, а інший з великим, ви виявите, що човен з більшою опорою потребуватиме меншої потужності для переміщення з заданою швидкістю, ніж той, що має малу опору.

Fan-jets покладаються на цей принцип, щоб забезпечити більш ефективну тягу до літака, ніж турбореактивні. У вентиляторному реактивному двигуні турбіна або турбіни приводять як компресор, який працює на повітрі, що йде в камеру згоряння, так і великий вентилятор, який додає імпульсу великій масі повітря, що йде навколо ядра двигуна без використання для спалювання палива. Цей вентилятор або «байпас» повітря потім змішується з більш високою швидкістю сердечника, продуктами згоряння, щоб дати високий імпульс загальний вихлоп двигуна, який отримує свій імпульс від великої маси байпасного потоку і високої швидкості основного потоку.

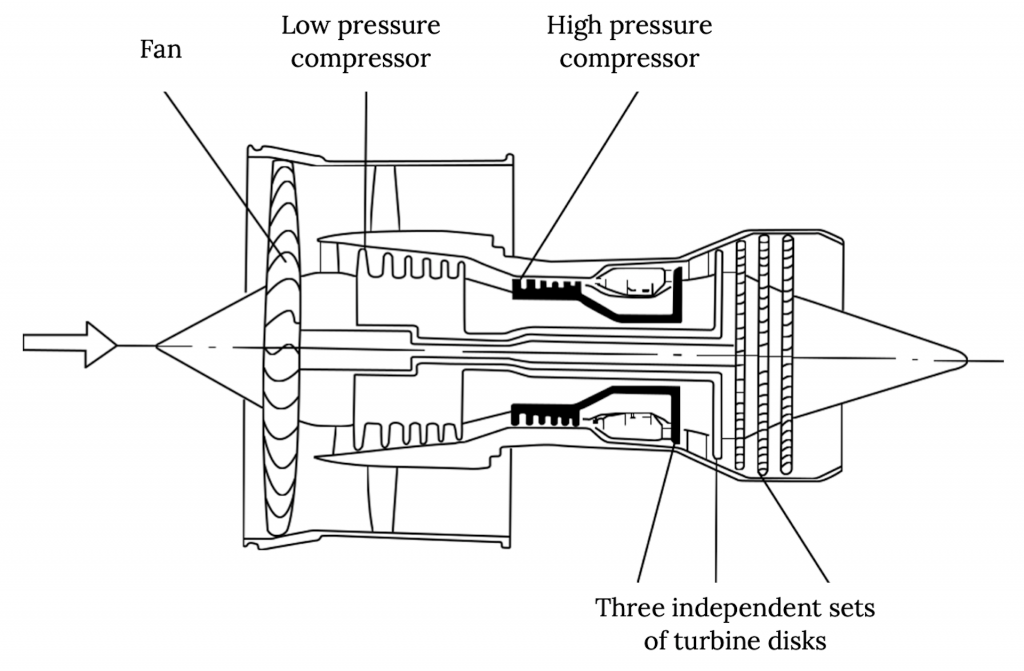
Наведено поперечний переріз для турбовентиляторного косою турбореактивної двигуна. Повітря надходить повз початкового вентилятора, з двома шляхами після цього: зовнішніми краями обходять двигун цілком і виходять з конструкції, а центральні ділянки ведуть до компресора низького тиску, який потім подається в компресор високого тиску. Після обох компресорів повітря потім басує через три незалежні набори турбінних дисків, перш ніж вийти з сопла в задній частині двигуна. — Малюнок 2.2: Ілюстрація турбовентиляторного або вентиляторного двигуна

Отже, для заданої величини тяги нам знадобиться задана величина зміни імпульсу повітря, що проходить через двигун між його входом і виходом. Про те, як ця зміна імпульсу математично пояснює тягу трохи пізніше. Справа тут в тому, що найефективнішим способом отримати цю зміну імпульсу з мінімальними втратами є прискорення великої маси повітря на невелику кількість (невелика зміна швидкості). Це означає, що чим більше коефіцієнт байпаса (відношення байпасної повітряної маси до маси повітря, що проходить через сердечник двигуна), тим ефективніше двигун. Але для цього є межа.

Оскільки реактивний двигун вентилятора стає більшим завдяки більш високій конструкції байпасу, корпус двигуна (гондола) також стає більшим, і він виробляє більше опору. Так що в якийсь момент має сенс замінити байпасний «вентилятор» великим пропелером. В результаті виходить «турбогвинтовий» двигун.

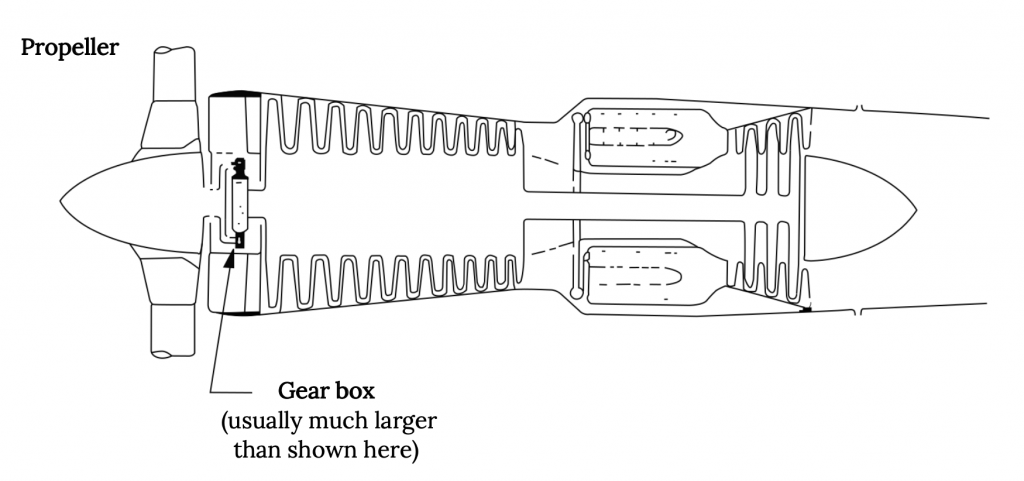
Перетин турбогвинтового двигуна показує гвинт спереду, з'єднаний з коробкою передач в центрі. Коробка передач потім з'єднується з додатковими лопатками компресора, камерою згоряння і турбінними вентиляторами, але це не є основним джерелом тяги. — Малюнок 2.3: Ілюстрація турбогвинтового двигуна

У турбогвинтовому двигуні потік через сердечник двигуна дійсно не використовується для отримання будь-якої значної тяги. Вихлопна турбіна призначена для того, щоб приймати всю енергію, яку вона може від вихлопу, щоб приводити в рух гвинт, і вся тяга двигуна надходить від потоку через гвинт. У турбогвинтовому двигуні кількість тяги, що надходить від основного потоку, настільки незначна, що в деяких конструкціях двигунів основний потік фактично йде «назад».

Ми можемо задатися питанням, якщо турбогвинтовий двигун є більш ефективним, ніж вентилятор реактивний, який, в свою чергу, більш ефективний, ніж турбореактивний, чому вентилятори є двигуном вибору для більшості літаків сьогодні? Відповідь - в бажаній швидкості польоту.

Подібно до того, як на крилі є великий підйом опору, коли воно наближається до швидкості звуку, є втрати типу перетягування на лопаті гвинта, коли його швидкість наближається до одиниці Маха. Фактично, для заданої швидкості обертання гвинта межа практичного діаметра для опори визначається радіусом, при якому перетин лопаті гвинта досягає свого критичного числа Маха. І, оскільки швидкість польоту, яку бачать лопаті гвинта, є функцією як їх швидкості обертання, так і швидкості літака, це обмежує швидкість літака. Конструкція гвинта може дещо розширити цей діапазон швидкостей за допомогою таких речей, як підмітали наконечники леза, але турбогвинтовий завжди накладає обмеження на круїзні швидкості літаків.

Крім того, виявляється, що частоти обертання, необхідні для турбогвинтового гвинта, на порядок нижче тих, що знаходяться в ефективному сердечнику турбіни, і це вимагає редукторів швидкості між турбіною та опорою, і це вносить як шум, так і вібрації, які не зустрічаються в вентилятор-струмені.

2.2 Пропелерні двигуни

Так в чому ж різниця між турбогвинтовим і гвинтовим гвинтом, що приводиться в дію двигуном внутрішнього згоряння? З точки зору тяги, що забезпечується гвинтом, особливої різниці немає. Різниця полягає в двигуні і зачепленні, що приводить в рух пропелер.

Турбогвинтовий двигун приводиться в рух невеликим турбінним (реактивним) двигуном, який посилає якомога більшу частину своєї енергії на гвинт через карданний вал і систему редукторів. Пропелер двигуна IC прикріплений до карданного валу двигуна внутрішнього згоряння, який, як і більшість автомобільних двигунів, використовує спалювання бензину або дизельного палива в двигуні поршневого/циліндрового типу для повороту вала.

Сьогодні більшість двигунів внутрішнього згоряння знаходяться на менших літаках авіації загального призначення. Цей тип двигуна забезпечував надійну, доступну потужність для літаків з моменту першого польоту братів Райт в 1903 році. Протягом багатьох років було багато захоплюючих варіацій двигуна IC, що використовуються в літаках, від «роторних» двигунів Першої світової війни, в яких карданний вал був прикріплений до літака, а гвинт і двигун фактично оберталися разом навколо валу, до масивних поршневих двигунів 1940-х і 1950-х років. з десятками циліндрів, розташованих навколо карданного вала, як ядра на колосі кукурудзи, до чотирьох і шести циліндрів, типу автомобіля, але з повітряним охолодженням, двигуни, як правило, зустрічаються на сучасних літаках GA. Ці багато різновидів двигунів IC зробили б цікаве та виснажливе дослідження самі по собі, але це виходить за рамки цього тексту.

Що стосується нас, пропелерний двигун - це гвинтовий двигун, незалежно від того, чи приводиться в рух турбіною, двигуном IC або гумовою стрічкою. Нас просто хвилює «потужність», що виводиться двигуном, і ми будемо називати це «потужністю валу» незалежно від типу двигуна, який приводить в рух вал.

2.3 Тяга і потужність

Це підводить нас до головної відмінності в тому, як ми будемо говорити про рух для реактивних і опорних двигунів. Для реактивних літаків, будь то турбореактивні або вентилятори, ми охарактеризуємо рухові властивості літака з точки зору тяги. Для літаків, що працюють на гвинтах, незалежно від того, прикріплений гвинт до двигуна IC або турбіни, ми поговоримо про продуктивність з точки зору потужності.

Потужність і тяга - це лише два різних способи погляду на рух літака та продуктивність. Вони безпосередньо пов'язані один з одним через швидкість.

Потужність = (тяга) (Швидкість)

Хоча ми зазвичай говоримо про реактивний рух з точки зору тяги та рушійної установки з точки зору потужності, є мало підстав поза конвенцією, що ми повинні це зробити. Ми могли б говорити про потужність реактивного двигуна і тягу гвинта, і ми іноді робимо це. Можливо, однією з причин цієї відмінності є те, що пізніше нам буде зручно дивитися на зміну як потужності, так і тяги зі швидкістю, і ми виявимо, що прийнято вважати, що тяга досить постійна зі швидкістю для струменя, а потужність досить постійна зі швидкістю для площини, що рухається гвинтом.

Агрегати, зазвичай пов'язані з потужністю і тягою, відповідно, є фунти і кінські сили. Так, це «політично некоректні» одиниці; тим не менш, вони набагато ширше використовуються, ніж Ньютони і Уоттс, їх еквіваленти СІ. [Ви коли-небудь чули, щоб хтось говорив про потужність свого автомобільного двигуна у ватах?] Це, звичайно, означає, що нам потрібно дізнатися, як одиниця кінських сил відноситься до базових агрегатів в «англійській» системі.

1 кінська сила = 550 фут-фунтів/секунду.

[Трохи інженерних дрібниць: це перетворення використовувалося так часто в дні розрахунків правил слайдів, що більшість правил слайдів мали спеціальну позначку на них у місці 550 на слайді.]

2.4 Закони тяги та збереження

Щоб з'ясувати, як такі речі, як висота та швидкість повітря, впливають на тягу та потужність, нам потрібно поглянути на те, як повітря проходить через пропелер або реактивний двигун, коли літак знаходиться в польоті, і як змінюється імпульс повітря, як це слідує за цим шляхом. Для цього нам потрібно буде подивитися на два «закони збереження», збереження маси і збереження імпульсу.

2.4.1 Збереження маси

У найпростішій концепції збереження маси часто констатується щось на кшталт «маса не може бути ні створена, ні знищена; тобто вона постійна або збережена». Це часто супроводжується класифікатором, який зазначає, що в атомній реакції маса фактично може бути створена (реакція синтезу) або зруйнована (реакція поділу). Це цікавий спосіб подивитися на масу, якщо хтось дивиться на масу у Всесвіті або в закритому контейнері, але це не допомагає нам, коли ми говоримо про двигуни. Потрібно дивитися на збереження маси в потоці; тобто в повітрі, що проходить через кімнату або трубу або пропелер або реактивний двигун.

Якби у нас було герметичне приміщення, наповнене повітрям, було б просто стверджувати, що кількість повітря в приміщенні є постійною. Ми могли б мати людей і рослини в кімнаті з хімічними реакціями, які є частиною людського дихання і рослинної хімії, постійно змінюючи хімічні складові в «повітрі»; тим не менш, загальна маса «повітря» залишатиметься постійною.

Картина змінюється, коли ми додаємо вентиляцію в кімнату, або використовуючи систему примусової вентиляції, таку як система кондиціонування або опалення, або просто відкриваючи вікна та двері. З будь-якою системою буде нове повітря, що надходить у вікна, двері або впускні вентиляційні отвори та старе повітря, що виходить з інших вікон, дверей або витяжних вентиляційних отворів. Якби у нас було приміщення лише з примусовим впуском повітря і без витяжки, маса повітря в приміщенні збільшувалася б, коли повітря надходило через вхідний отвір. Для розміщення цієї зростаючої маси приміщення доведеться або розширюватися, як повітряна куля, або тиск і щільність повітря в приміщенні повинні були б збільшуватися. Відзначимо, що, якби ми припустили, що повітря «нестисливий», неможливо буде закачати нове повітря в приміщення, не забезпечивши витяжку рівної кількості повітря для виходу. Для цього буде потрібно збереження в масі повітря в приміщенні.

Так на прикладі вентиляції приміщення збереження маси для повітря в приміщенні буде просто означати, що в міру надходження маси нового повітря в приміщення повинна покинути приміщення така ж кількість маси повітря. Кімнатні або віконні кондиціонери працюють таким чином, приймаючи задану масову витрату з приміщення, відправляючи його через охолоджуючі змійовики, і повертаючи ту саму масову витрату в приміщення після того, як з повітря було видалено деяке тепло.

Це підводить нас до теми масової витрати, яку часто називають «m-dot» і задано символ нижнього регістру «m» з крапкою зверху літери, щоб представляти похідну від маси за час; тобто маса в одиницю часу, dm/dt.

Коли ми говоримо про кімнату з вентиляційними отворами або дверима та вікнами, ми повинні говорити про масові витрати, і ми говоримо, що для збереження маси ми не повинні мати змін маси в приміщенні за одиницю часу, просто інший спосіб сказати, що кількість маси, яка надходить протягом певного періоду часу, повинна дорівнювати кількість маси, яка виходить за цей же час. Це стверджується як:

дм/дт = 0.

Іншими словами, кількість маси в приміщенні не змінюється з часом.

Ми часто ставимо це у формі рівняння, кажучи, що

дм/дт = σ ρ ВА = 0.

Тут ми говоримо про те, що масова витрата дорівнює щільності повітря, помноженої на його швидкість, так як він проходить через площу розміром «А». Іншими словами, якщо повітря на рівні моря щільність дме через вікно зі швидкістю 20 футів в секунду, і якщо це вікно має отвір 2 фути на 4 фути, ми можемо обчислити масу повітря за одиницю часу, що проходить через вікно.

дм/дт = ρ ВА = (0,002378 сл/фут ³) (20 футів/сек.) (2 фути х 4 фути) = 0,3805 сл/сек.

[Зауважте тут, що одиниці масової швидкості потоку були виявлені слимаками в секунду. У системі СІ вони будуть знаходитися в кілограмах в секунду, а у версії «англійської» системи, часто використовуваної в таких галузях, як машинобудування, одиниці масової витрати будуть фунтів-маса в секунду. .]

Тепер, якщо збереження маси дотримано для повітря в приміщенні, така ж маса повітря за одиницю часу повинна виходити з іншого отвору або отворів.

(дм/дт) _в+ (дм/дт) _вихід = 0

або

(ρ ВА) _в + (ρ ВА) _вихід = 0

Отже, якщо є єдине вікно, що пропускає повітряний потік, знайдений вище, а вихід через двері, ми можемо використовувати збереження маси, щоб визначити швидкість повітря, що виходить за двері.

(ρ ВА) _вихід = — (ρ ВА) _в.

Так само, як три фактори, розмір (площа) вікна, швидкість потоку повітря через вікно, і щільність повітря, визначали «масову витрату» повітря, що надходить в приміщення, ті ж три речі визначають вихідну масову витрату. Насправді всі три ці речі можуть бути різними на виході (в даному випадку двері), тому, якщо ми хочемо знайти швидкість повітря, що виходить, ми повинні знати як площу дверей, так і щільність повітря біля дверей. Однак немає ніяких причин, чому повітря, що протікає через приміщення, змінило б щільність, тому ми безпечно припускаємо «нестисливий» потік, тобто щільність постійна. Це дає нам просте рівняння:

(VA) _вихід = — (ВА) _в.

Отже, якщо двері 3 фути в ширину на 7 футів у висоту, даючи площу 21 футів ², тоді як вікно має площу 8 футів ², швидкість повітря, що виходить з дверей, становить:

_{V _{виходи/V} _в = — A в/A _вихід}

або

_{V _вихід = — V _в (A в/A _вихід)}

або в цьому випадку

^{V _вихід = — 20 фут/сек. (8 футів 2/21 фут ²) = — 7,62 фут/сек.}

Тепер, чому стоїть знак мінус зі швидкістю виходу? Це тому, що ми без реальної причини вирішили дати позитивний сенс швидкості, що йде у вікні, і оскільки швидкість є вектором; тобто вона має напрямок, ми позначили потік повітря в кімнату як позитивний. Це означає, що негативний знак на швидкості виходу повітря говорить нам, що він виходить з приміщення. Хоча це може здатися непотрібним ускладненням тут, є випадки, коли це може допомогти нам зрозуміти, що відбувається.

Наприклад, припустимо, що в нашій кімнаті п'ять вікон і дві двері, і нам кажуть, що повітря надходить у всі п'ять вікон з певною швидкістю і виходить з однієї двері з заданою швидкістю, що відбувається біля інших дверей? Потік через ці другі двері входить або виходить з кімнати?

Нам доведеться написати повне рівняння для збереження масового потоку, щоб знайти як кількість, так і напрямок потоку через другі двері.

(ρ ВА) _w ₁ + (ρ ВА) _w2 + (ρ ВА) _w3 + (ρ ВА) _w4 + (ρ ВА) _w5 — (ρ ВА) _Д1 + (ρ ВА) _Д2 = 0.

Зверніть увагу, що ми призначили позитивні значення потоку через всі вікна, оскільки нам сказали, що потік надходить у всі з них. Ми також призначили від'ємне значення потоку з перших дверей, оскільки потік, як кажуть, виходить з цих дверей. Також зверніть увагу, що ми не призначили знак (напрямок) потоку через другі двері, тому що ми поняття не маємо, в який бік він йде. Тепер, якщо ми помістимо всю необхідну інформацію для п'яти вікон та перших дверей у терміни рівняння, і якщо ми знаємо площу другої двері і припустимо, що щільність скрізь однакова (нестисливий потік), ми можемо вирішити для швидкості (швидкості) потоку, використовуючи співвідношення збереження маси вище і знайти як величину швидкості, так і її напрямок (знак).

Вправа 2.1

Спробуйте зробити вищезазначену проблему, припускаючи, що всі п'ять вікон мають розмір 2 фути X 4 фути, і що повітря дме зі швидкістю 20 футів/сек.

Припустимо, що дві двері мають розмір 3 футів X 7 футів і що потік з перших дверей вимірюється в 50 футів/сек.

Знайти швидкість і напрямок потоку через другі двері.

ПРИМІТКА: Тут ми розглянули весь потік в нашу «систему» або «регулятор гучності» як ПОЗИТИВНИЙ, а весь потік з системи як НЕГАТИВНИЙ. Якщо ми не знаємо його напрямку, ми припускаємо, що воно позитивне за значенням, і рішення рівняння дасть нам негативну відповідь, якщо ми припустимо неправильний напрямок. Пізніше, коли ми дивимося на рівняння імпульсу, ми будемо використовувати одиничний вектор, п, щоб призначити позитивний напрямок в межах нашої обраної системи осі для потоку через отвір, і цей блок вектор завжди буде вказувати OUT з системи.

Гаразд, це було досить просто, але як ми маємо справу з масовим збереженням, коли ми дивимося на потік через реактивний двигун або гвинт?

Збереження маси через гвинт або реактивний двигун працює так само, як збереження маси в потоці, що проходить через кімнату. Насправді, для реактивного двигуна це навіть простіше, ніж середня кімната, тому що є тільки один чітко визначений вхід і вихід, або це дійсно так?

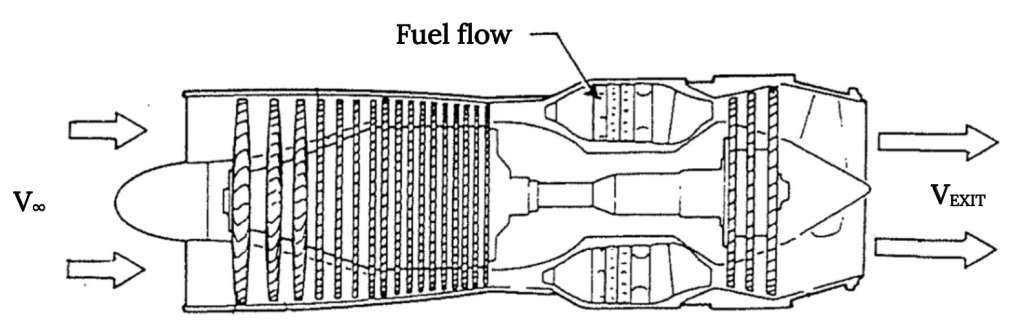
Поперечний переріз турбореактивного двигуна показує повітряний потік, що надходить зі швидкістю cpa V sub нескінченності, повинен спочатку пройти через кілька наборів лопатей компресора, коли він стискається на менші та менші ділянки. Потім він направляється повз камери згоряння, де потік палива контролює швидкість додавання палива для згоряння. Потім повітря розширюється через набір лопатей турбіни, виходячи з вихідного сопла на швидкості ковпачка V sub вихід. — Малюнок 2.4: Масові потоки для турбореактивного двигуна

Технічно, є друге джерело вхідної маси в будь-якому реактивному двигуні, і це масовий потік палива, що надходить в двигун. Існує повітря, що надходить у вхідний отвір двигуна відомої області з (нібито) відомою швидкістю та щільністю, але потік, що виходить з двигуна, насправді не просто повітря, це газ, який надходить від згоряння вхідного повітря та вхідного палива. Масова швидкість потоку, що виходить з виходу, повинна враховувати як масу повітря, що надходить, так і палива, що надходить, тому наші відносини збереження маси повинні це визнати.

(дм/дт) на _вході + (дм/дт) _паливо + (дм/дт) _вихлоп = 0

Зазвичай ми пишемо це як:

(ρ AV) на _вході + (дм/дт) _паливо = — (ρ AV) _вихлоп.

Тому ми повинні знати масову витрату палива. Зазвичай масова витрата палива дуже мала порівняно з витратою повітря на вході, тому, можливо, цим терміном можна знехтувати. Так в чому ж велика справа? Якщо ми можемо знехтувати витратою палива, ми повертаємось до одного вікна, прикладом однієї двері та життя легко. На жаль, є ще один фактор, про який ми не повинні забувати, і це щільність. Зазвичай потік через вихлоп реактивного двигуна йде досить швидко, близько або більше, ніж швидкість звуку; тобто ми більше не можемо припустити, що щільність постійна, як ми це робили в прикладі вентиляції приміщення.

Щоб вирішити цю задачу, ми повинні знати або щільність вихідного потоку, або його швидкість, щоб вирішити рівняння для «іншого» параметра (вихідна швидкість щільності), і оскільки масовий потік палива сприяє цій щільності виходу, ми, ймовірно, не повинні вважати, що вона незначна, навіть якщо його швидкість майже майже мізерно малий.

Здійснення збереження маси для струменя ще більш складним є той факт, що більшість сучасних струменів є «вентиляторними струменями», де є по суті два вхідні потоки, один, який проходить через сердечник двигуна, змішуючи з паливом, утворюючи високошвидкісний вихлоп, а інший, більший, потік, який прискорюється через вентилятор. Ми можемо проаналізувати цю проблему, враховуючи два окремі вхідні потоки та два окремі вихідні потоки, або припускаючи (правильно у більшості випадків), що два вихідні потоки змішуються перед тим, як покинути покриття двигуна або «гондолу», утворюючи єдиний змішаний вихлоп.

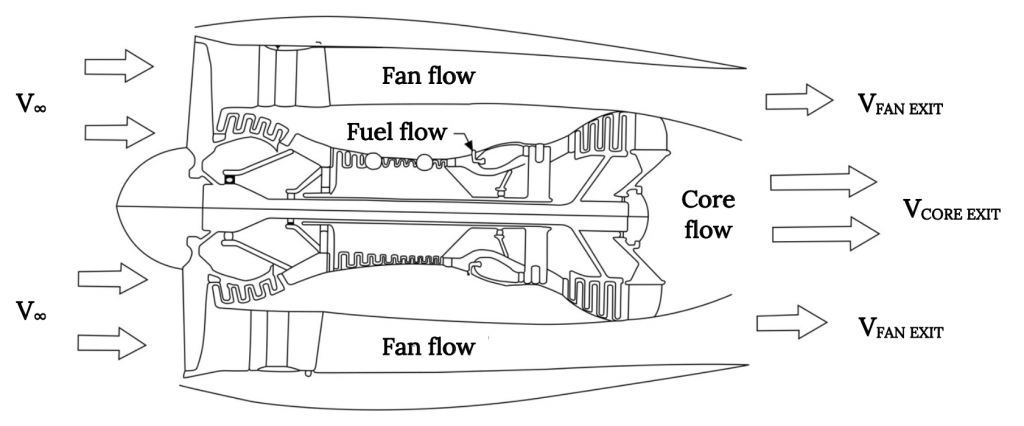
Поперечний переріз вентиляторного реактивного двигуна показує, що повітря, що надходить на швидкості ковпачка V sub нескінченності, має два шляхи. Зовнішні краї проходять вентилятор і продовжують безперервно виходити з задньої частини двигуна на швидкості ковпачка V sub вихід вентилятора. Центральні частини переміщаються через набір вентиляторів компресора в камеру згоряння, де потік палива визначає, скільки додається для горіння. Потім повітря проходить через вентилятори турбіни і виходить як основний потік, зі швидкістю ковпачка V підсердечника виходу. — Малюнок 2.5: Протікає через вентилятор-реактивний двигун

У будь-якому випадку, проблема потоку реактивного двигуна для багатьох людей трохи простіше зрозуміти, ніж проблема потоку гвинта, оскільки зони входу та виходу, як правило, досить добре визначені. Як ми визначаємо вхідні та вихідні потоки, коли ми проводимо потік через гвинт?

Коли потік проходить через гвинт, тільки які зони входу та виходу? Там дійсно немає фізичного входу або виходу. Звичайно, ми знаємо, що потік йде через сам пропелер, так чи використовується область пропелера як для «входу» потоку, так і для його «виходу»? Це навряд чи має сенс. Як можна говорити про зміни потоку між входом і виходом, коли між входом і виходом немає фізичної відстані?

Давайте розглянемо, що нам відомо інтуїтивно про протікання через пропелер (або вентилятор). Ми знаємо, що потік за гвинтом або вентилятором рухається швидше, ніж потік перед ним. Ми знаємо, що певним чином, таким чином, який можна детально проаналізувати, розглядаючи кожен гвинт або лопатку вентилятора як трохи обертається крило, яке працює на повітрі, пропелер по суті додає енергії потоку. Ми також знаємо, якщо трохи подумати про це, що ми не можемо використовувати рівняння Бернуллі для порівняння потоку вгору та нижче за течією опори або вентилятора, оскільки енергія додається на опору або вентиляторі, а рівняння Бернуллі передбачає, що енергія постійна через потік. Ми також знаємо, що існують обмеження на те, що може зробити вентилятор або гвинт для прискорення потоку через обмеження швидкості наконечника на самих лопатях, і ці обмеження по суті означають, що ми можемо досить безпечно припустити нестисливий потік через систему.

Зібравши всі ці факти воєдино, ми можемо намалювати картину, яка виглядає приблизно так, як потік повинен з'явитися через пропелер або вентилятор. Ми знаємо, що десь вище за течією гвинта потік не порушений; тобто він знаходиться у «вільному потоці» або атмосферних умовах. Ми знаємо, що десь нижче за течією опори статичний тиск у масі повітря, що пройшов через гвинт, має повернутися до його величини вільного потоку.

Ми уявимо собі «поток-трубка», або тривимірний шлях постійного масового потоку, який починається в непорушеному потоці вище за течією опори, проходить через опору (стаючи таким же діаметром, як опору в цьому місці, а потім продовжується нижче за течією до точки, про яку ми згадували вище, де статичний тиск повернувся до атмосферного значення. Як повинен виглядати цей «поток-трубка»?

Потік-трубка визначається як тривимірний шлях потоку, в якому масова швидкість потоку однакова в кожній точці її шляху. По суті, як показано на наступному малюнку, площа поперечного перерізу потоку-трубки (її площа «захоплення») повинна мати таку ж величину масової витрати через неї, як проходить через саму опору. Так само зона «виходу» для нашої потокової трубки також повинна дозволяти проходити той самий масовий потік, який пройшов через зону захоплення та зону опори «диска».

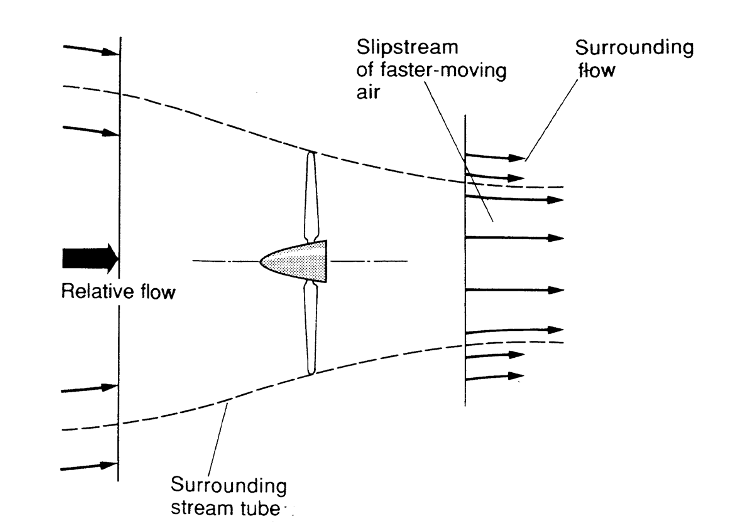
Коли відносний потік наближається до гвинта, труби потоку звужуються, щоб відповідати ширині гвинта, а потім продовжують звужуватися після проходження його. Ця звужена область призводить до ковзання потоку повітря, що швидше рухається всередині трубки потоку, тоді як навколишній потік повільніший. — Малюнок 2.6: Концепція потокової трубки для потоку гвинта

Так чому ж «поток-трубка» на малюнку вище стає поступово меншою, коли потік йде від атмосферного тиску, зони захоплення вільного потоку до зони виходу атмосферного тиску десь нижче за течією? По-перше, ми знаємо, що швидкість у зоні виходу повинна бути більшою, ніж у зоні захоплення (впуску); отже, якщо масовий витрата однаковий, а потік нестисливий, площа повинна зменшуватися у зворотній пропорції збільшенню швидкості. Але чому ми припускаємо, що це зменшення площі (і збільшення швидкості) плавне і безперервне? Хіба не просто великий стрибок швидкості через диск гвинта?

Ну, ми, мабуть, могли б проаналізувати все з точки зору якогось миттєвого стрибка швидкості потоку на диску гвинта на основі енергетичного балансу, припускаючи, що енергія, додана опорою, виробляє раптове збільшення кінетичної енергії та швидкості потоку. Однак з реальних вимірювань ми знаємо, що це збільшення швидкості не є миттєвим, і що частина збільшення спостерігається перед гвинтом, оскільки потік прискорюється від його швидкості «вільного потоку» до швидкості прямо на передній частині опорного диска. Ми також знаємо, що потрібно кілька діаметрів гвинта нижче за течією, перш ніж потік у «оправі» досягне максимальної швидкості. Виходячи з цього поєднання реальності та зручності, ми вирішили моделювати збільшення швидкості як безперервне в межах «потоку-трубки» у формі сходяться сопла круглого перерізу, як показано на малюнку вище.

Ця ідеальна картина, звичайно, ігнорує багато речей, таких як втрати через турбулентність та ефекти обертального потоку; тим не менш, це той, який працює досить добре. Отже, що ми пропонуємо зробити з цією моделлю і з моделлю потоку через реактивний двигун? Те, що ми хочемо зробити, це використовувати їх, щоб визначити, як виробляється тяга і знайти властивості, які визначають, як тяга змінюється в залежності від швидкості і висоти.

2.4.2 Тяга

Наша мета полягає в тому, щоб поглянути на рух. Як ми враховуємо тягу або потужність в оцінках продуктивності літаків?

Є два способи зробити це. Можна було б подивитися на енергетичні доповнення до потоку і збереження енергії. Але, як зазначалося в обговоренні гвинта вище, це було б дуже нудно, вимагаючи від нас робити аеродинамічний аналіз кожної лопаті гвинта, враховуючи втрати через ефекти стисливості біля кінчиків лопатей та перешкоди між потоком над однією лопаткою та наступним лезом. Є книги про те, як це зробити, найстаріша з яких йшла під такими назвами, як «Теорія повітряного гвинта», і це тип аналізу, який повинні використовувати компанії, що виробляють гвинти. Проблема була б ще цікавішою у реактивному двигуні, коли ми повинні враховувати енергетичні прибутки та втрати через обтікання лопатей компресора та лопатей турбін, згоряння палива та потоку через внутрішні форсунки.

Виявляється, найпростіший спосіб поглянути на тягу - це подивитися на збереження імпульсу.

2.4.3 Збереження імпульсу

Збереження імпульсу, як збереження маси та енергозбереження, є одним із «великої трійки» законів збереження, які ми всі бачили десь у деяких курсах фізики. На перший погляд, збереження імпульсу - це просте поняття. Так само, як і при масовому збереженні потоку, ми повинні враховувати всі масові потоки, які входять або залишають розглянуте поле потоку, дивлячись на збереження імпульсу, ми повинні враховувати всі речі, які могли б враховувати зміни імпульсу і, зрештою, сили.

По суті, концепція, яку ми розглядаємо, - це та, яка говорить про те, що зміна імпульсу в тілі або «системі» з часом повинна дорівнювати силам на цьому тілі чи системі. Ідея полягає в тому, що або сили на тіло або систему призведе до зміни його імпульсу або зміна імпульсу всередині системи або тіла призведе до сили.

(д/дт) (імпульс) = (д/дт) (мв) = сила

Це проста ідея, яка часто змушена виглядати дуже складною, коли виведена в більшості підручників з механіки рідини. Якщо, наприклад, ви штовхнете футбольний м'яч, сила, яку ви надаєте м'ячу, призведе до зміни імпульсу м'яча. Якщо м'яч стояв на місці, перш ніж його ногами, сила змінить свій імпульс з нуля на значення, пов'язане з силою удару і масою м'яча. Якщо м'яч вже рухався, удар може відправити рух в іншому напрямку, тому це поняття є спрямованим; тобто це векторна концепція, як і слід було очікувати, коли задіяна сила.

Дивлячись на рух літака, ми зацікавлені в зворотній дії; тобто створення зміни імпульсу для того, щоб отримати силу, змінюючи імпульс потоку через двигун або гвинт для створення тяги.

Так само, як у роботі з рівнянням Бернуллі у нас був вибір моделювання потоку як рухомої рідини, що проходить повз крила або тіла, або як тіло, що рухається по нерухомому повітрю, ми повинні зробити подібний вибір тут. Ми, наприклад, вирішимо дивитися на потік через реактивний двигун або гвинт так, ніби двигун (опора) стоїть на місці, а потік рухається повз нього. Це дійсно вибір між тим, щоб враховувати імпульс рухомого двигуна або імпульс рухомого повітря. Будь-який вид дасть однакову відповідь за тягу, але рухома повітряна модель зазвичай трохи легше працювати. У будь-якому випадку, ми повинні бути дуже обережними, щоб врахувати всі можливі зміни імпульсу як в двигуні, так і в потоці.

Спочатку нам потрібно подивитися, які зміни імпульсу можуть бути присутніми, а також які сили можуть бути залучені. Для цього розглянемо один з найпростіших «реактивних» двигунів, але один з найскладніших для аналізу, гумовий балон, який надувається і відпускається.

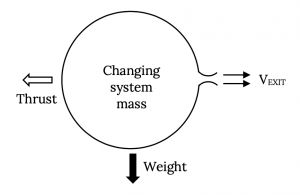
Оскільки загальна маса балона змінюється через повітря, що виходить через отвір, газ виходить з кришкою швидкості V суб вихід вправо, в результаті чого чиста сила тяги вліво. Вони перпендикулярні силі ваги вниз повітряної кулі. — Малюнок 2.7: Повітряна куля як простий струмінь

Давайте подивимося на ілюстрацію вище та перерахуємо всі способи, які імпульс може відігравати певну роль, а також усі залучені сили. Буде принаймні два джерела зміни імпульсу для повітряної кулі та принаймні три сили, які можуть бути залучені.

Джерела зміни імпульсу:

Зміна імпульсу повітряної кулі («системи») з часом через зміну маси повітря всередині повітряної кулі з часом і через будь-які зміни швидкості цієї маси. [Коли повітряна куля виганяє повітря через вхід/вихід, маса самої «системи» змінюється, і навіть якщо її швидкість була постійною, імпульс системи зміниться.]
Імпульс потоку, що виходить з «системи» (балона); тобто масовий потік повітря через впуск/вихід (струмінь) помножений на його швидкість.

Обидва ці терміни вище спрямовані через швидкостей, пов'язаних з ними. Імпульс самого повітряної кулі пов'язаний зі швидкістю повітряної кулі, а імпульс потоку через вихід, очевидно, пов'язаний з напрямком потоку через вихід.

Сили на повітряній кулі:

Основною силою на повітряній кулі буде та, яку ми вирішимо назвати тягою. Це, по суті, те, що ми намагаємося знайти.
Інша сила на повітряній кулі, про яку ми могли б не думати спочатку, полягає в тому, що через гравітацію; тобто його вага.
Нарешті, були б будь-які сили тиску, спричинені тиском, що діють на райони. Вони можуть включати тиск на саму повітряну кулю або різниці тиску через межі системи. Часто ми виявляємо, що сили тиску, як правило, балансують або підсумовуються до нуля, але є деякі випадки, коли їх потрібно враховувати.
Ми також могли б розглянути сили тертя або навіть електромагнітні або інші сили, якщо хочемо, але ми обмежимося першими трьома силами, згаданими вище.

Як ми описуємо кожне з цих джерел зміни імпульсу або сил дуже загальним чином? Давайте розглянемо кожен з перерахованих вище.

1. Зміна імпульсу «системи» з часом передбачає зміни як маси, так і швидкості системи:

d/dt [(маса) (швидкість)],

і, оскільки маса системи може бути записана як її щільність разів її обсяг, ми могли б розглядати це як

d/dt [(щільність) (об'єм) (швидкість)]

2. Зміна імпульсу через потік з (і взагалі) в систему з часом - це, по суті, масова швидкість потоку (dm/dt) через будь-які входи або виходи, помножена на швидкість, з якою ця маса проходить через зони входу або виходу. Ми знаємо, що масова швидкість потоку - це щільність, помножена як на швидкість, так і на площу поперечного перерізу потоку, тому цей термін виражається як:

(дм/дт) (швидкість) = (щільність) (швидкість) (площа) х (швидкість).

3. Вага - це якраз маса (щільність х обсяг), помножена на прискорення сили тяжіння.

(Щільність) (обсяг) (г).

4. Сили тиску - це лише тиск, що діє на ділянку:

(тиск) (площа)

Тепер, щоб працювати з усіма цими, нам потрібно скласти їх у вигляді якогось рівняння. Рівняння має по суті сказати, що зміни імпульсу повинні бути збалансовані задіяними силами. Це можна розглядати як сили, що викликають зміну імпульсу (нога футболіста штовхає м'яч) або зміни імпульсу, що викликають сили (тяга від випущеної повітряної кулі). Рівняння, яке зазвичай виникає в результаті набагато більш формального похідного, є складним виглядом, векторним зв'язком, який називається рівнянням імпульсу.

2.4.4 Рівняння імпульсу

$ДДТРРРР+Sρ Vθ (V⟩ ⋅N^) DSЗміна імпульсу рідини = −Fe−Sρn^ds+rρgdrсили, що викликають зміну імпульсу$

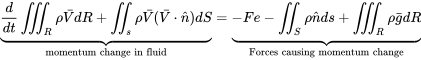
Перш ніж панікувати на векторні позначення і подвійний і потрійний інтеграли, зробіть глибокий вдих і подивіться, як ці терміни співвідносяться з представленими вище.

Потрійний інтеграл над «R» (математична «область» або «система») - це не що інше, як обсяг. Якщо щільність і швидкість всього, що міститься в області або системі, однакові; тобто, якщо це однорідна система, то цей термін є нічим іншим, як похідною від густини за часом, що умножує об'єм на швидкість; тобто маса системи збільшує її швидкість, як це було заявлено в розділі вище.

Так чому ж ми робимо це так складно виглядати? Однією з причин може бути просто справити враження на наших друзів в гуманітарних мистецтвах або показати нашим батькам, наскільки важкі наші курси. Краща причина - дозволити рівнянню імпульсу враховувати неоднорідні системні ефекти. Припустимо, наприклад, що наша «система» представляла собою не повітряну кулю, наповнену приємним однорідним повітрям, а м'яч для бейсболу або гольфу з твердою начинкою з декількох шарів, кожен з різною щільністю, і далі, що хтось зробив м'яч з його більш важким ядром кілька «поза центром». Ви можете купити такі «трюк» м'ячі для гольфу в магазинах новинок і коли ви потрапили в них клюшкою для гольфу (надати силу системі!) , замість того, щоб подорожувати по прямій лінії, вони коливаються навколо, ніби вони п'яні. Оскільки рівняння імпульсу може враховувати це «неоднорідність», це може пояснити хиткий рух трюку м'яч для гольфу. Аналогічним чином останній термін праворуч, гравітаційний або ваговий термін, може враховувати гравітаційні ефекти на неоднорідну масу.

Два члена рівняння мають подвійні інтеграли. Ви, можливо, вже здогадалися, що подвійний інтеграл на відстані «S» повинен стосуватися якоїсь області, і дивлячись на терміни підтвердить це. Подвійний інтегральний термін зліва відноситься до імпульсу, що переноситься з потоком в систему або з неї над зоною входу або виходу. Цей термін пишеться таким складним способом, щоб мати можливість враховувати нерівномірні швидкості над входом або виходом і навіть для нерівномірних щільностей над цими ділянками. Якщо припустити, що весь вхідний або вихідний потік є тією ж рідиною, що рухається з однаковою швидкістю, то умови щільності та швидкості можуть вийти за межі інтеграла, а сам інтеграл стає нічим іншим, як зоною входу чи виходу. Отже, знову ж таки, чому це виглядає так складно? Ну, у багатьох випадках потік з отвору не є рівномірним, оскільки сили тертя змушують його рухатися повільніше біля країв отвору, ніж у центрі, і ця всеосяжна форма рівняння імпульсу може пояснити це, якщо ми хочемо, щоб це зробити. Аналогічно, термін тиску на правій стороні рівняння може враховувати зміну тиску на поверхні.

А як щодо векторного позначення, члена V • n, у подвійному інтегральному члені ліворуч? По-перше, рівняння імпульсу - це векторне рівняння, що означає, що кожен з членів має напрямок, і рішення рівняння для такої сили, як тяга або тяга, дасть як величину, так і напрямок для цієї сили. По-друге, для одного з членів з кожної сторони рівняння, тільки параметр «нормальний» до певної поверхні або межі, який спричинить силу, а «одиничний вектор» n використовується для позначення цього нормального напрямку. Ми завжди будемо визначати напрямок для цього вектора одиниці як вказує на систему, навіть там, де потік надходить у систему.

Що ж тоді означають ці векторні величини? Кожна з швидкостей може мати в них до трьох членів, один пов'язаний з кожним напрямком у вибраній системі осей. У випадку швидкості в умовній системі осей x, y, z ми зазвичай використовуємо терміни u, v та w для позначення x, y та z складових швидкості відповідно. Отже, ми б написали вектор швидкості як:

V = у я+ v j + ш к,

де i, j та k - одиничні вектори в додатних напрямках x, y та z. Подібним чином вектор гравітації може мати до трьох компонентів; однак іноді ми намагаємося визначити нашу систему координат, щоб одна вісь була в напрямку прискорення гравітації, щоб усунути дві з цих компонентів.

Термін V • n - це «точковий добуток» двох векторів, де обидва вектори V і n можуть мати компоненти x, y та z, але тільки подібні спрямовані компоненти множаться один з одним, а потім сума, щоб дати «скалярну» величину з величиною, але немає напряму. Отже, якщо швидкість знаходиться в тому ж напрямку, що і вектор нормалі (як це часто буває для потоків у систему або з неї), результатом є просто величина швидкості. На іншій крайності, якщо швидкість знаходиться під кутом 90 градусів до вектора нормалі, точковий добуток дає нуль.

Знову можна запитати, навіщо робити речі настільки складними з усіма цими інтегралами та векторами та точковими добутками тощо? Це робиться таким чином, оскільки це дуже універсальне рівняння, яке може враховувати повністю тривимірний рух. Наприклад, якщо футболіст штовхнути м'яч під кутом 90 градусів до існуючого напрямку руху, це співвідношення буде, за умови, що ми знали силу удару і масу і швидкість м'яча, повідомити нам новий напрямок і швидкість м'яча, хоча напрямок буде ні в початковий напрямок руху або в напрямку удару. Аналогічно, якщо в трубі є вигин, ми можемо використовувати рівняння, щоб знайти величину та напрямок сили, яка виникне, коли вода протікає через цей вигин в трубі.

Хитрість у використанні рівняння імпульсу полягає в тому, щоб слідувати правилу, яке часто відрізняє інженера від чистого вченого або математика; тобто використовувати правильне вирівнювання систем осей і встановити межі системи і зробити хороші припущення, які усунуть якомога більшу складність. На щастя, ми можемо зробити багато цього, оскільки ми використовуємо рівняння імпульсу, щоб подивитися на тягу.

2.4.5 Тяга (знову)

Давайте подивимося на потік через реактивний двигун з точки зору рівняння імпульсу.

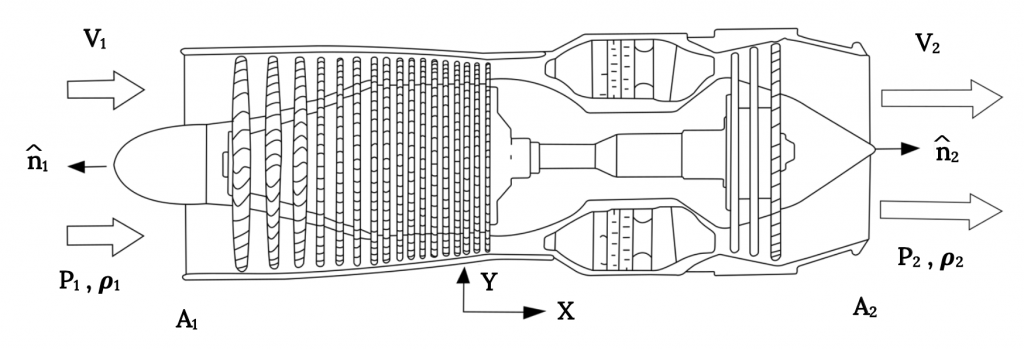
На впуску для турбореактивного двигуна з площею цоколя A sub 1 нормальні точки назовні, вліво, при цьому повітря, що надходить в двигун при швидкості ковпачка V sub 1, кришка тиску P sub 1, і щільність rho sub 1, введіть праворуч. На виході з площі ковпачка A sub 2, нормаль вказує назовні, праворуч, вирівнюється з вихідним потоком повітря при швидкості ковпачка V sub 2, кришка тиску P sub 2 і щільності rho sub 2. — Малюнок 2.8: Умови рівняння імпульсу для турбореактивного літа

На ілюстрації вище ми вирівняли двигун з віссю «x», і ми маємо потік, що надходить у вхідний отвір двигуна у напрямку x і інший потік, що виходить з двигуна, також у напрямку x. Ми хочемо знати тягу як функцію цієї інформації. Давайте розглянемо, що можна сказати про різні терміни в рівнянні імпульсу.

Перший член в лівій частині рівняння є «залежним від часу» терміном для обліку зміни імпульсу самої «системи» з часом. Тут наша система - це весь реактивний двигун, і, якщо припустити, що двигун (літак) знаходиться в «стійкому» або постійному швидкісному польоті, немає нічого в терміні (щільність, швидкість або обсяг), що змінюється з часом. Отже, цей термін дорівнює нулю.

Другий термін зліва враховує імпульс, що переноситься в систему або з неї, коли потік входить або залишає. Очевидно, що цей термін не піде, оскільки ми маємо повітря, що надходить у двигун, а продукти згоряння виходять на інший кінець. Спочатку нам потрібно запитати, чи є ці два потоки «рівномірними» у відповідних зонах входу чи виходу. Якщо можна припустити, що вони рівномірні і можна вважати, що весь потік має однакову щільність, то цей термін (власне два члени, один для входу і один для виходу) стає:

ρ ₁ В ₁ (В ₁ •п ₁) А ₁ + ρ ₂ В ₂ (В ₂ •п ₂) А ₂.

Тепер, що ми робимо з векторним бізнесом? Потоки обидва знаходяться в позитивному напрямку x. Перший нормальний одиничний вектор знаходиться у від'ємному напрямку x, а другий - у додатному напрямку x. Результатом є:

— ρ ₁ V ₁ ² A ₁ + ρ _₂ V ² A ₂, (все в напрямку х)

Добре, що піклується про ліву частину рівняння імпульсу. Що відбувається з умовами праворуч? Перший термін праворуч - це «зовнішня» сила, яка, в даному випадку, є тягою, яку ми хочемо знайти. Другий термін праворуч, мабуть, найважче зрозуміти фізично, тому ми повернемося до цього.

Третій термін праворуч - це термін тяжкості, насправді вага. Якщо ми припустимо, що це діє під кутом 90 градусів до осі x або напрямку польоту і, таким чином, перпендикулярно всім іншим силам і змінам імпульсу, в яких ми маємо інтерес, ми можемо просто нехтувати цим терміном. Насправді правильніше було б сказати, що його складова в напрямку x дорівнює нулю. Насправді цей термін сказав би нам, що повинна бути сила протистояти вазі, і це був би аеродинамічний підйом, який, в свою чергу, був би пов'язаний у рівнянні імпульсу з вертикальною зміною імпульсу потоку, коли він рухався навколо крила та відповідного розподілу тиску навколо крило. По суті, ми обираємо ігнорувати вертикальні складові сил та зміни імпульсу.

Тепер повернемося до другого терміну праворуч, єдиного терміну з тиском в ньому. Цей термін розглядає сили, спричинені тиском, що діють на райони. Якби ми дивилися на силу підйому, ми б використали цей термін, щоб інтегрувати розподіл тиску навколо крила. На двигуні ми будемо вважати, що потоки по зовнішній стороні корпусу двигуна або гондоли симетричні, тобто такий же розподіл тиску існує у верхній частині, як і на нижній частині гондоли, і що чистий ефект цих тисків (принаймні в напрямку x) дорівнює нулю. Але як щодо тиску на вході та виході?

Тиск через вхід і вихід?!! Як це може означати що-небудь, коли тут немає реальних поверхонь, просто потоки йдуть або виходять? Тут цікавим стає поняття «системної» межі. Коли існує реальна межа, така як гондола двигуна, межі системи легко зрозуміти. Але ці «відкриті» кінці «системи» також є межами, за якими ми повинні враховувати всі терміни в рівнянні. Іншими словами, так само, як ми повинні були враховувати потік через ці дещо уявні межі, ми також повинні враховувати зміни тиску через них. Але як цей тиск може викликати реальні сили, коли немає «реальних» поверхонь, на які вони могли б діяти? Це стає одним із тих «стрибків віри», які ми часто повинні робити, застосовуючи рівняння до фізичних ситуацій.

Ні, немає поверхонь на вході та виході, де перепади тиску на поверхні викликають силу; однак ми повинні враховувати їх у будь-якому випадку, якщо існує перепад тиску між навколишньою атмосферою та потоком у вхід та вихід. Це, мабуть, найпростіше зрозуміти, коли ми дивимося на потік вихлопних газів.

Виходить з вихлопу - це потік продуктів згоряння повітря і палива, який був нагрітий і нагнітається під тиском в камері згоряння двигуна. Після згоряння ми хочемо перетворити цю додану енергію в максимально високий імпульс (другий член на лівій стороні рівняння імпульсу), наскільки це можливо. Це означає, що ми хочемо максимально «розширити» газ у вихідному патрубку, знижуючи його тиск з відповідним збільшенням швидкості (рівняння Бернуллі) максимально, щоб отримати високий імпульс. Ідеальна ситуація - розширити його до того моменту, коли виходить газ має такий же тиск, як і атмосфера, в яку він буде виходити. Якщо він розширюється занадто сильно або занадто мало, будуть втрати, коли тиск потоку приходить до рівноваги з атмосферою. Виявляється (і рівняння імпульсу по суті говорить нам про це), що втрати від понад або недостатнього розширення еквівалентні силі тиску, яка була б на поверхні з тією ж площею, що і вихід з різницею тиску, рівною тій, що під або надмірним розширенням Delta-p. Ось чому деякі високопродуктивні струмені мають вихідні форсунки змінної площі на своїх двигунів.

Та ж проблема може виникнути в меншій мірі на вході двигуна, але правильно спроектований вхід двигуна та секція компресора може усунути більшу частину втрат.

Отже, як ми маємо справу з цим терміном тиску? Ми або повинні знати різницю між атмосферним тиском та потоками входу та виходу та обчислювати значення для цих термінів, обережно враховуючи належним чином знаки одиничного вектора, або ми повинні припустити, що ці втрати незначні. Давайте зробимо легкий вихід і припустимо, що ці терміни не мають великого значення, оскільки у нас є правильно розроблений двигун.

Гаразд, де це нас залишає? Ми закінчили з відносно простим рівнянням:

— ρ ₁ В ₁ ² А ₁ + ρ ₂ В ₂ 2 А ₂ = — Fe

переставляючи це дає:

Тяга = Fe = ρ ₁ В ₁ ² А ₁ — ρ ₂ В 2 ² А ₂.

Дивлячись на це, ми бачимо, що другий член праворуч буде набагато більше першого члена, а значить, тяга буде мати негативний знак. Це нормально? Звичайно, це так. Він просто говорить, що сила тяги знаходиться в негативному напрямку х, вліво, так само, як ми хочемо, щоб це було.

Ого! Це, звичайно, було багато роботи, щоб отримати досить очевидну відповідь; тяга дорівнює зміні імпульсу від входу двигуна до виходу! Хіба це не дещо інтуїтивно? Так, це начебто інтуїтивно для багатьох з нас. З іншого боку, це робить математиків та теоретиків у нашому середовищі щасливими, і що ще важливіше, це говорить нам про те, що, досягнувши цієї «інтуїтивної» відповіді, ми зробили деякі важливі припущення щодо тиску. поведінка і вибір системи осей і т.д.

Добре, тепер, коли ми маємо все, що під нашими поясами, які важливі факти про рух можуть бути зроблені з цього рішення? Щоб переконатися в цьому, давайте трохи пограємо з рівнянням вище, враховуючи збереження маси.

Тепер, визнаючи, що V ₁ - це наша швидкість «вільного потоку», V _∞, і що щільність повітря, що входить, також є щільністю атмосфери, ρ _∞, ми можемо записати це як

Тяга = ρ _∞ В _∞ ² А ₁ — ρ ₂ В 2 ² А ₂

І дивлячись тільки на величину тяги (як було сказано вище, співвідношення вище дає негативну тягу, позначаючи просто те, що вона знаходиться зліва на нашій оригінальній ілюстрації двигуна, що рухається справа наліво)

Тяга = ρ ₂ В ₂ ² А ₂ — ρ _∞ В ∞ ² А ₁

Тепер визначаємо «статичну тягу» як T ₀, тягу, коли двигун стоїть на місці (V _∞ = 0). Це величина тяги, яка буде вимірюватися на випробувальному стенді двигуна і є стандартною інформацією, яка існувала б для будь-якого двигуна.

Т ₀ = ρ ₂ В ₂ ² А ₂

Це дозволяє нам переписати загальні відносини тяги як:

Тяга = Т ₀— ρ _∞ В _∞ ² А ₁,

або просто як:

Т = Т ₀ — А В _∞ ²,

де:

а = ρ _∞ А ₁

Про що нам все це говорить? По-перше, всі рівняння тяги говорять нам про те, що тяга - це функція щільності атмосфери. На відміну від швидкості, яку ми раніше виявили, змінюється з квадратним коренем щільності, тяга зменшується прямо пропорційно зменшенню щільності в атмосфері. Таким чином, пишемо:

Т _альт = Т _сл (ρ _альт/ρ _сл)

Це важлива залежність між тягою і висотою, яку ми будемо використовувати у всіх розрахунках продуктивності.

По-друге, дізнаємося, що в цілому тяга двигуна змінюється в залежності від швидкості відповідно до співвідношення:

Т = Т ₀ — а В _∞ ²

Слід зазначити, як завжди, що ці рівняння передбачають важливі припущення, такі як припущення, що тиск на виході двигуна і тиск на вході обидва рівні тиску в атмосфері вільного потоку. Пілоти реактивних літаків скажуть вам, що тяга до статичної тяги, показана вище, не враховує, наприклад, сплеск двигуна на початковому прискоренні вниз по злітно-посадковій смузі, як «ефект таран» у вхідному отворі двигуна відбувається. Цей «ефект барана», по суті, є одним із цих ефектів тиску, які ми вирішили ігнорувати.

2.4.6 Тяга гвинта

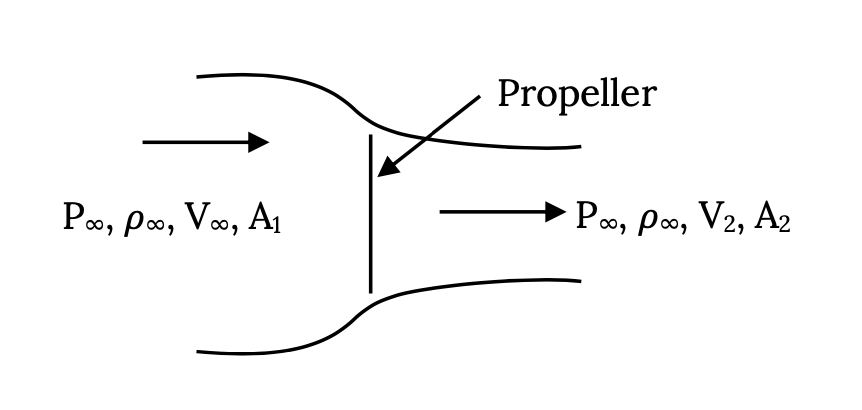
Слід зазначити, що ми отримаємо по суті точно таке ж рівняння тяги, дивлячись на потік через гвинт, як ми робимо з реактивним двигуном. Маючи на увазі більш раннє обговорення, ми б намалювали нашу «систему», як показано нижче, використовуючи межі, які представляють «потокову трубку» постійного масового потоку. У цьому випадку у нас немає простого способу дізнатися точні значення для вхідної площі потоку або області виходу, але ми отримаємо точно таке ж рівняння, як ми знайшли для струменя, і ми все одно знайдемо.

Т = Т ₀ — а V _∞ ².

Повітряний потік наближається до гвинта з кришкою тиску P sub нескінченності, щільністю rho sub нескінченності, ковпачком швидкості V sub нескінченності та кришкою площі A sub 1. Потім повітря виходить повз гвинта з тим же тиском і щільністю, але оновлена швидкість ковпачка V sub 2 і зменшена площа ковпачка A sub 2. Упорний ковпачок T як і раніше показано рівним статичному завзятому ковпачку T вузла мінус швидкість звуку в рази ковпачок V sub нескінченності в квадраті. — Малюнок 2.9: Умови рівняння імпульсу для потоку гвинта

У цьому розділі ми розглянули відносно прості моделі двигунів літаків, які ми будемо використовувати при вивченні продуктивності літаків. При цьому ми використовували деякі основні фізичні поняття збереження (маса та імпульс), обидва з яких можуть забезпечити дуже потужні інструменти для оцінки сил та рухів у потоках рідини та інших областях. Ми зробили багато спрощення припущень на цьому шляху, щоб зрозуміти деякі дуже основні поняття, пов'язані з реактивним і гвинтовим двигуном; зокрема, дати основу для моделювання того, як тяга і потужність змінюються в залежності від швидкості і висоти. Ці поняття ми знайдемо дуже корисними в наступних розділах.

Домашнє завдання 2

1. В аеродинамічній трубі швидкість змінюється в міру зміни площі поперечного перерізу тунелю. Якщо швидкість у квадратному тестовому розділі 6 ′ x 6 ′ в 100 миль/год, яка була швидкість вище за течією тестової секції, де тунель вимірює 20 ′ х 20 ′? Використовуйте збереження маси і припускайте нестисливий потік. Збереження маси вимагає, щоб при русі потоку через шлях або канал добуток щільності, швидкості та площі поперечного перерізу повинен залишатися постійним; тобто що ρ vA = постійна.

2. Модель тестується в аеродинамічній трубі зі швидкістю 100 км/год.

(a) Якщо потік у випробувальній секції знаходиться в стандартних умовах рівня моря, який тиск у точці стагнації моделі?

(b) Швидкість тунелю вимірюється за допомогою піто-статичної трубки, підключеної до манометра U-трубки. Що таке показання на цьому манометрі в дюймах води.

Посилання

Малюнок 2.1: Клер Колвін (2021). «Ілюстрація турбореактивного двигуна». CC ПО 4.0.

Малюнок 2.2: Клер Колвін (2021). «Ілюстрація турбовентилятора або вентилятор-реактивного двигуна». CC ПО 4.0.

Малюнок 2.3: Клер Колвін (2021). «Ілюстрація турбогвинтового двигуна». CC ПО 4.0.

Малюнок 2.4: Клер Колвін (2021). «Масові потоки для турбо-реактивного двигуна». CC ПО 4.0.

Малюнок 2.5: Клер Колвін (2021). «Протікає через вентилятор-реактивний двигун». CC ПО 4.0.

Малюнок 2.6: Джеймс Федорович Марчман (2004). «Концепція потокової трубки для потоку пропелера». CC ПО 4.0.

Малюнок 2.7: Родинний сірий (2021). «Повітряна куля як простий струмінь». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/2.1_20210804

Малюнок 2.8: Клер Колвін (2021). «Терміни рівняння імпульсу для турбореактивного літака». CC ПО 4.0.

Малюнок 2.9: Родинний сірий (2021). «Терміни рівняння імпульсу для потоку гвинта». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/2.9_20210804

<! — pb_fixme —><! — pb_fixme —>