6: Діапазон і витривалість

Last updated

Oct 25, 2022
Save as PDF
- 5: Зміна висоти - Підйом і керівництво
- 7: Прискорена продуктивність - Зліт і посадка

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Вступ

Трохи фону

У перші дні силового польоту основною проблемою було отримання літака в повітря і назад вниз безпечно (з безпечним значенням здатності кульгати після «посадки»). Знаменитий перший політ Райт був коротшим, ніж футбольне поле, і навіть протягом декількох років після грудня 1903 року вони задовольнялися об'їздом сімейної ферми. Вбудовані двигуни Райт не могли працювати протягом тривалого періоду часу, і вони просто не уявляли необхідності або бажання польотів над відстані понад кілька миль. Однак у 1908 році журнал Scientific American кинув виклик авіаційним експериментаторам, щоб виготовити літак або «аеролітак» ^[1], який міг літати, на громадський погляд, на відстані однієї милі! Хоча Райт стверджував, що може зробити такий політ, їх одержимість секретністю, як вони шукали військових продажів і їх егоїстичне переконання, що ніхто інший не може підійти до їх досвіду в авіації змусили їх ігнорувати приз, запропонований Науковий американський за одну милю громадського польоту.

Саме Гленн Кертісс, будівельник мотоциклетних двигунів і володар численних світових рекордів швидкості в мотогонках, який в липні 1908 року здійснив перший публічний одномильний політ. Кертісс, який працював з Олександром Белом та іншими, щоб розробити власні літаки, здійснив політ з журналістами газети, які спостерігали та з відеокамерами, що фіксують політ. Кертісс став головним авіатором в Америці, і Райтс були в люті, що призвело до численних судових позовів, як Уілбур і Орвілл прагнули довести в судах, що Кертісс і Белл порушили свої патенти. Кертісс продовжував перевершувати Wrights та інших у авіаційних зустрічах в Америці та Європі. Наступні патентні позови Райта, спрямовані на збереження для себе єдиних прав на проектування та будівництво літаків у Сполучених Штатах, застоювали розвиток літаків в Америці і змістили сцену авіаційного прогресу в Європу, де вона залишалася до Першої світової війни.

Оскільки авіація і авіація продовжували розвиватися, дальність і витривалість стали основною метою в проектуванні літаків. На війні бомбардувальники потребували великих дистанцій, щоб досягти ворожих цілей за межі лінії фронту, і до кінця Першої світової війни величезні бомбардувальники були розроблені в декількох країнах. Після війни європейські уряди субсидували перетворення цих гігантів в пасажирські літаки. Деякі більші літаки навіть були побудовані як пасажирські транспортні засоби до конфлікту. Ранні проекти Сікорського є хорошими прикладами. У Сполучених Штатах, однак, з невеликим інтересом уряду в просуванні повітряних подорожей для громадськості до кінця 1920-х років, розвиток літаків великої дальності був більше фантазії, ніж факт. У 1927 році трансатлантичний політ Ліндберга захопив уяву громадськості і інтерес до дальнього польоту збільшився. Політ Ліндберга, як і Кертісс, був підказаний призом від друкованих ЗМІ, що ілюструє роль газет і журналів у стимулюванні технологічного прогресу.

До кінця 1930-х років громадськість почала розглядати політ як спосіб подорожувати на великі відстані за короткий час, національні та міжнародні маршрути авіакомпаній розвивалися, а літаки на кшталт «China Clipper» встановили стандарти дальності та витривалості. Друга світова війна змусила людей і уряди мислити в глобальному плані, що призвело до розвитку у воєнний час бомбардувальників, здатних безперервно літати понад тисячі миль, а також до післявоєнних трансконтинентальних і транс-океанічних літаків. З 1903 року ми бачили, як авіаційні діапазони переходять від ніг до безперервного кружляння земної кулі, і витривалості йдуть від хвилин до днів!

6.1 Використання та вага палива

При вивченні дальності та витривалості ми повинні вперше в цьому курсі розглянути використання палива. У літаках Кертіса і Райта не рідкість двигун кидав від механічних проблем або перегріву до того, як закінчилося паливо. У сучасних літаках дальність і витривалість залежать від кількості палива на борту. Коли минула остання крапля палива, літак досяг межі дальності та витривалості. Можна, звичайно, включити діапазон ковзання та витривалість після того, як літак закінчується паливо, але авіакомпанія, яка працювала таким чином, приверне мало пасажирів!

Використання палива залежить від конструкції двигуна, налаштувань дросельної заслінки, висоти та ряду інших факторів. Однак мета цього тексту не полягає в вивченні паливної економічності двигуна або використання пілотом дросельної заслінки. Ми будемо вважати, що нам дають двигун з певними специфікаціями щодо ефективності та використання палива, і що налаштування дросельної заслінки є тим, що зазначено в довіднику літака або керівництві для оптимальної дальності або витривалості на обраній висоті. Передбачається, що студент пройде окремий курс з руху для вивчення витоків фігур, використовуваних тут для цих параметрів.

Нашою першочерговою проблемою у використанні палива буде зміна ваги літака з часом. Багато з наших рівнянь продуктивності, що використовуються в попередніх розділах, включають вагу літака. У тих главах ми розглядали вагу як постійну. Вага, в дійсності, постійний тільки для планера або вітрильника. Для інших літаків вага завжди змінюється, завжди зменшується в міру спалювання палива. Це означає, що аеродинамічні показники літака змінюються під час польоту. Це, однак, не скасовує цінності методів, використовуваних раніше для вивчення круїзу і підйому. Ці розрахунки, як правило, виконуватимуться з використанням максимальної ваги брутто літака, що призведе до консервативного або «гіршого випадку» аналізу цих параметрів продуктивності. Ми також можемо використовувати методи, розроблені раніше, щоб подивитися на «миттєві» можливості літака при заданій вазі, розуміючи, що в більш пізній час в польоті і при меншій вазі продуктивність може бути різною.

При розгляді дальності та витривалості вкрай важливо розглядати вагу як змінну, змінюючись від максимальної ваги брутто під час зльоту до порожньої ваги паливного бака в кінці польоту. Для цього ми будемо мати справу з використанням палива з точки зору ваги палива (на відміну від обсягу палива, в галонів, який ми зазвичай використовуємо для автомобілів). Коли наша турбота - витривалість, нас цікавить зміна ваги палива за одиницю часу.

$\dfrac{dW_f}{dt}$

і, коли діапазон викликає занепокоєння, ми хочемо знати, як вага палива зменшується з пройденою дистанцією.

$\dfrac{dW_f}{dS}$

Виробники авіаційних двигунів люблять вказувати використання моторного палива з точки зору питомої витрати палива. Для реактивних двигунів це тяга стає питомою витратою палива, а для опорних літаків - питомою потужністю споживання палива. Оскільки тяга і потужність приносять різні одиниці в рівняння, ми повинні розглянути два випадки окремо.

6.2 Дальність і витривалість: Jet

Ми говоримо про вихід двигуна реактивного двигуна з точки зору тяги; отже, ми говоримо про використання палива реактивного двигуна з точки зору тяги питомої витрати палива, С _т. C _t - маса палива, споживаного за одиницю часу на одиницю тяги. Одиницею часу повинні бути секунди, а агрегат для тяги повинен бути в фунтах або ньютонах тяги.

[C _t] = (sl/sec) /фунт _тяга, або = (кг/сек) /N _тяга

Вище наведено _{правильне} визначення тяги питомої витрати палива, однак, насправді це не зовсім те, що нам потрібно для наших розрахунків. Ми б вважали за краще визначення, засноване на вазі споживаного палива замість маси. Ми таким чином визначимо вагу питомої витрати палива, _т, як вага використовуваного палива за одиницю часу на одиницю тяги. Це дає одиниці (час) ^-1.

$\left[\gamma_{\mathrm{t}}=\mathrm{gC}_{\mathrm{t}}\right]=\left(\mathrm{lb}_{\text {fuel }} / \mathrm{sec}\right) / \mathrm{lb}_{\text {thrust }}, \text { or }=\left(\mathrm{N}_{\text {fuel }} / \mathrm{sec}\right) / \mathrm{N}_{\text {thrust }}=(\mathrm{sec})^{-1}$

Читач повинен знати, що багато текстів виконання літаків і текстів руху дуже розпливчасті щодо одиниць питомої витрати палива. Деякі навіть визначають його з точки зору маси і дають йому одиниці 1/сек., роблячи його розмірно неправильним. Частина плутанини, особливо в старих американських текстах руху, полягає у використанні фунт-маси як одиниці маси. Це дає комбінацію фунтів маси, розділеної на фунти сили, яка насправді дає сек. ^2/фут. Потім ситуація ще більше ускладнюється автором, здавалося б, кидаючи термін, який називається g _c, який повинен вирішити проблему lb _m /lb _f. У будь-якому випадку дуже важливо, щоб інженер, використовуючи питомий витрата палива, ретельно розглянув задіяні агрегати перед початком вирішення проблеми діапазону або витривалості. Правильно вказана вага питома витрата палива матиме одиниці сек ^-1 і буде робити це без використання чогось, що називається g _c.

Слід додати, що можна також зіткнутися з питомою витратою палива, яка була розрахована з використанням маси палива (кг) і тяги в кілограмах, що не є SI одиницею, яка використовується в більшій частині світу (практично ніхто в світі не знає, що таке Ньютон або як його використовувати). Якщо це зроблено, числове значення має бути таким же, як отримано за допомогою визначення ваги питомої витрати палива вище.

Деякі джерела питомих даних про витрату палива використовують одиниці (годин) ^-1, оскільки година є більш зручною одиницею часу. Використання секунд, однак, правильне в будь-якій стандартній системі одиниць, і студенту може бути добре пораджено перетворити години в секунди перед початком обчислення, хоча це в кінцевому підсумку призведе до обчислення витривалості в секундах, даючи досить великі числа для відповідей.

Щоб знайти витривалість, ми хочемо, щоб швидкість зміни маси палива (W _f) за одиницю часу, яку можна записати з точки зору тяги, питомої витрати палива.

$\mathrm{dW}_{\mathrm{f}} / \mathrm{dt}=\gamma_{\mathrm{t}} \mathrm{T}$

І, в прямому і рівному польоті, де тяга дорівнює перетягуванню

$\mathrm{d} \mathrm{W}_{\mathrm{f}} / \mathrm{dt}=\gamma_{\mathrm{t}} \mathrm{D}$

Для максимальної витривалості ми хочемо мінімізувати вищевказаний термін. Це чітко показує, що для максимальної витривалості реактивний літак повинен літати при мінімальних умовах опору. Ми розглянемо, як знайти цю витривалість після короткого погляду на діапазон.

Щоб знайти дальність польоту, ми повинні дивитися на швидкість зміни маси палива з дальністю польоту. Ми могли б трохи зупинитися на цьому етапі, щоб зрозуміти, що це може бути складніше, ніж витривалість, тому що дальність буде залежати більше, ніж просто аеродинамічні характеристики літака. Також буде потрібно враховувати швидкість вітру. Літак може літати назавжди зі швидкістю 100 миль/год на зустрічний вітер 100 миль/год і все ще мають діапазон нуля! Наразі, однак, ми відкладемо ці турботи і подивимося на просту математику, з якої ми починаємо розгляд проблеми. Вище ми розглянули швидкість зміни ваги з часом. Ми можемо поєднати це зі зміною відстані з часом (швидкістю), щоб отримати швидкість зміни ваги з відстанню.

$\mathrm{dW}_{\mathrm{f}} / \mathrm{dS}=\left(\mathrm{dW}_{\mathrm{f}} / \mathrm{dt}\right) /(\mathrm{dS} / \mathrm{dt})=\gamma_{\mathrm{t}}(\mathrm{T} / \mathrm{V})=\gamma_{\mathrm{t}}(\mathrm{D} / \mathrm{V})$

Зверніть увагу, що ми все ще припускаємо D = T або прямий і рівний політ.

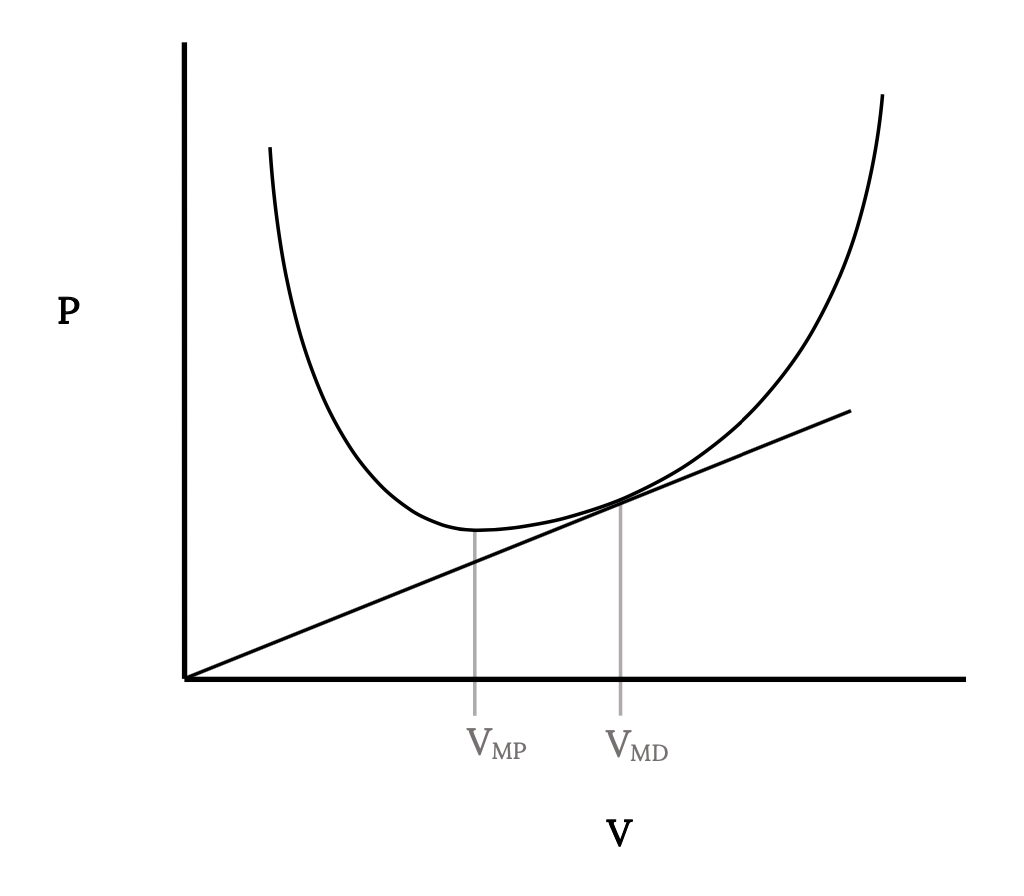
З вищесказаного очевидно, що максимальний діапазон буде відбуватися, коли перетягування, розділене на швидкість (D/V), є мінімальним. Це не умова, яку ми вивчали раніше, але ми можемо отримати деяке уявлення про те, де це відбувається, дивлячись на графік опору проти швидкості для літака.

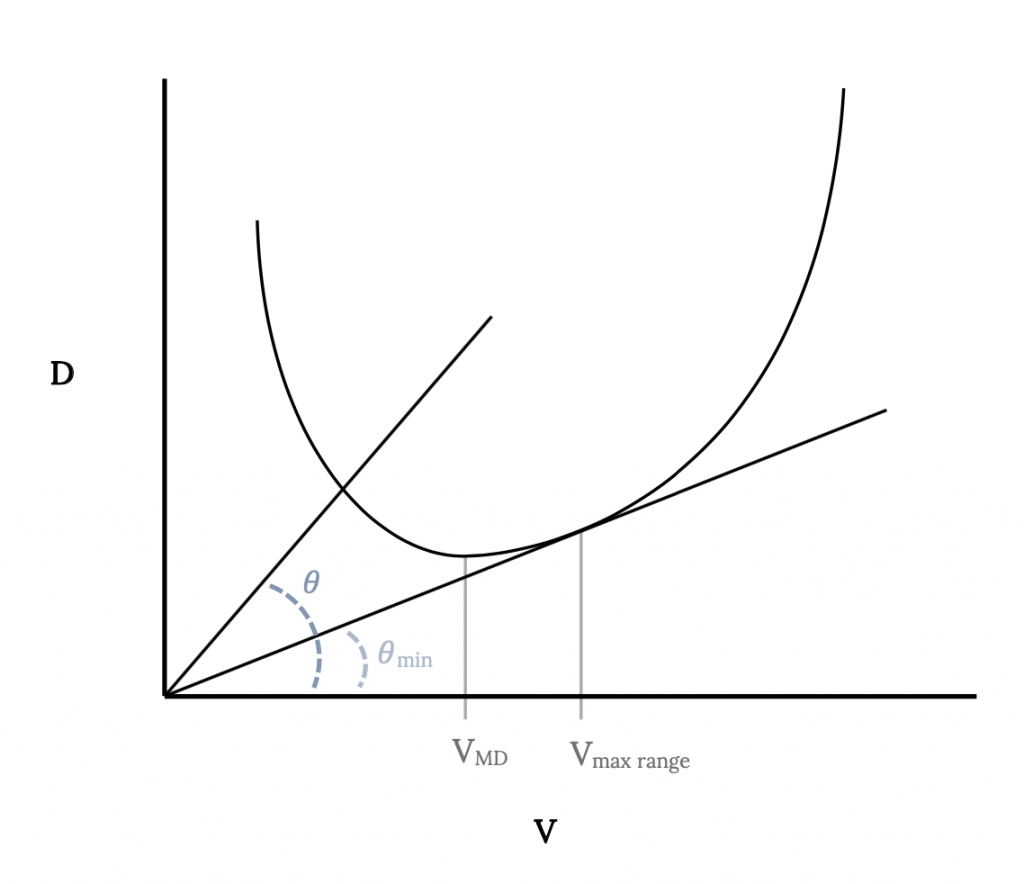
Графік показує перетягування ковпачка D на вертикальній осі, тоді як кришка швидкості V - горизонтальна вісь. Крива перетягування нагадує параболу, з правою стороною злегка сплюснута. Від початку до кривої перетягування проводиться довільна лінія під кутом тета над горизонтальною віссю. Другу лінію проводять дотичною до кривої під відповідним кутом тета суб хв, перетинаючи пряму зі швидкістю для максимального діапазону, cap V sub max діапазону. Найнижча точка на кривій перетягування виникає на ковпачку V sub cap M cap D. — Рисунок 6.1: Пошук швидкості для максимального діапазону

На цьому графіку лінія, проведена від початку, щоб перетинати криву перетягування в будь-якій точці, має дотичну, рівну перетягуванню в точці перетину, поділену на швидкість у цій точці. Мінімально можливе значення D/V для літака, представленого кривою перетягування, слід знайти тоді, коли лінія просто дотична до кривої перетягування. Ця точка дасть швидкість для максимальної дальності. Зверніть увагу, що це більш висока швидкість, ніж для мінімального опору (яке, в свою чергу, було вище швидкості при мінімальній потужності).

У вищесказаному ми знайшли умови, необхідні для досягнення максимальної дальності та витривалості для реактивного літака. Ми ще не знайшли рівнянь для фактичного діапазону або витривалості. Щоб знайти їх, нам потрібно повернутися до диференціалів часу та відстані та інтегрувати їх. На час у нас є

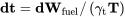
$ДТ = паливо DW/ (γTT)$

Тепер ми хочемо поставити рівняння у формі, яка включає вагу літака замість ваги палива. Так як зміна ваги літака в польоті дорівнює і протилежно вазі споживаного палива.

dW = — дВ _паливо

у нас є

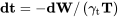
$ДТ = −дВ/ (γTT)$

Нарешті, інтеграція з часом, щоб знайти витривалість дає

$Е = −W1W2dWγTT$

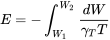
Аналогічним чином діапазон знаходить від диференціала відстані.

$DS = −VDW/ (γTT)$

або

$R = −W1W2ВДВ γТТ$

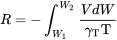
У вищезазначених рівняннях ми повинні знати, як швидкість літака, тяга та питома витрата палива змінюються залежно від ваги літака. На цьому етапі нам потрібно зробити деякі припущення про те, як буде здійснюватися політ. Це іноді називають «розкладом польотів».

6.3 Приблизні рішення для дальності та витривалості для струменя

Перше припущення, яке слід зробити при знаходженні рівнянь дальності та витривалості, полягає в тому, що політ буде по суті прямим і рівним. Для того, щоб дати собі деяку вільність, ми назвемо цей політ «квазі - рівня», наше бажання полягає лише у використанні відносин L = W T = D.

Т = Д = Ш (Д/Л) = Ш (С _Г /С _Л),

і ми також можемо використовувати

$v=2WρСКЛ$

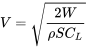
Замінюючи їх у діапазон і витривалість відносини вище дають

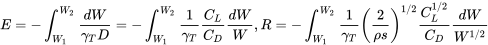
$е = −w1w2dwγTD = −W1W21γТК КДДДВВ, Р = −W1W21γT (2ρ с) 1/2 кЛ1/2КДДДВВ1/2$

На цьому етапі нам потрібно зробити деякі подальші припущення щодо розкладу польотів, щоб спростити інтеграцію цих рівнянь. Наприклад, в рівнянні витривалості, якщо припустити, що політ здійснюється під постійним кутом атаки, ми припускаємо

що коефіцієнти підйому і опору є постійними для всього польоту. Якщо ми також припустимо, що питома витрата палива постійна для польоту, єдиною змінною, що залишилася в інтегралі, є сама вага, а інтеграл стає:

$Е = −1 γТК СД W1W2dW = 1 γТК КДЛН (W1W2) (конста α)$

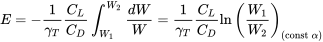
Інтеграл діапазону містить додаткову змінну, щільність атмосфери. Ще можна зробити пару комбінацій припущень, які призведуть до простої інтеграції та реалістичних умов польоту. Перший випадок буде припустити круїз як на постійній висоті, так і на постійному куті атаки, що дає як щільність, так і коефіцієнти підйому і опору як константи в інтеграції.

$R = 2⋅2γt⋅ρSCL1/2cD (W1−W2) (конста αконст V)$

Другий простий випадок поєднує в собі припущення про постійний кут атаки і постійної швидкості, які можуть бути використані з більш ранньою формою рівняння дальності.

$R = −w1w2ВВГТ = −W1W2ВГТК КДДДДВ$

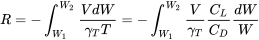
подача

$R = V γТКЛДЛН (W1W2) (конст αконст V)$

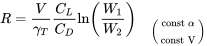
Зверніть увагу, що останнє рівняння вище - це просто рівняння витривалості, помножене на швидкість. Це не повинно дивуватися, оскільки це той випадок, коли швидкість постійна.

У остаточних рівняннях вище для дальності та витривалості слід зазначити, що якщо використовуються стандартні одиниці з питомими витратами палива в сек. ^-1, дальність буде вказана в футах або метрах, а витривалість у секундах. Нам може бути легше з'ясувати, наскільки наші відповіді реалістичні, якщо ми перетворимо ці відповіді на милі або кілометри та години.

У пошуку вищевказаних рівнянь для діапазону та витривалості ми розглядали лише окремі випадки, які призведуть до простих інтеграцій. Якщо ми знаємо більш складні графіки польотів, ми можемо визначити функціональні зв'язки між коефіцієнтами підйому та опору, швидкістю, щільністю тощо та втратою ваги під час польоту та вставити їх у вихідні інтеграли для вирішення дальності та витривалості. Вищезазначені випадки, однак, дуже близькі до фактичних експлуатаційних умов круїзу для літаків великої дальності і, ймовірно, буде достатньо для вступного дослідження продуктивності літаків. Давайте подивимося на ці прості випадки.

Обидва випадки діапазону включали наше припущення витривалості постійного кута атаки та питомої витрати палива. Перший випадок поєднав ці припущення зі специфікацією постійної висоти. Це, здається, найпростіший випадок, щоб насправді літати, але щоб побачити, що це насправді означає, нам потрібно повернутися до прямого і рівного співвідношення швидкості польоту.

V = [2Вт/ (ρ СК _Л)] ^1/2

або VW ^1/2, коли ρ і d C _L обидва постійні.

Якщо висота (щільність) і кут атаки (коефіцієнт підйому) є постійними, очевидно, що швидкість повинна змінюватися в міру зміни ваги. Іншими словами, для цього розкладу польотів у міру спалювання палива і зменшення ваги літака швидкість польоту повинна зменшуватися пропорційно квадратному кореню ваги.

Інший випадок, постійна швидкість у поєднанні з постійним кутом атаки, видно з співвідношення швидкості вище, щоб вимагати зменшення щільності пропорційно вазі.

Вт/ρ = конст. коли V і C _L постійні.

Це означає, що коли літак спалює паливо, літак буде повільно рухатися на більш високі висоти, де щільність нижча. Це загальновідоме як розклад рейсів дрейфу. Це насправді дуже схоже на те, як комерційні авіалайнери літають міжміські маршрути. Ті з вас, хто був на таких рейсах, згадають пілота, який оголосив, що «ми зараз круїмо на 35 000 футів і піднімемося на 39 000 футів після перетину Міссісіпі» або якийсь такий план. Хоча FAA не дозволить літакам просто «дрейфувати», коли вони літають від узбережжя до узбережжя, вони дозволять графіки, які поступово наближають техніку дрейфу.

Слід зазначити, що два рівняння діапазону вище дадуть дві різні відповіді на однакову кількість палива. Також відзначимо, що рівняння засновані тільки на круїзній частині польоту. Фактичний політ включатиме зліт, підйом на висоту круїзу, спуск і посадку на додаток до круїзу. Також необхідно зробити надбавку на резервне паливо для обробки надзвичайних ситуацій і «трюмів», накладених авіадиспетчерами.

Найбільше припущення, яке використовується у всіх вищезгаданих інтеграціях, - це постійний кут атаки. Хоча це відповідає нашим умовам для оптимальних випадків, таких як максимальна витривалість

що відбувається при максимальному співвідношенні ліфт-перетягування (мінімальний опір), він може не дуже добре відповідати реальному польоту. Хоча пілот може легко контролювати свою повітряну швидкість і висоту, кут атаки літака не так легко контролювати і безпосередньо контролювати.

Наведені вище рівняння для дальності та витривалості дійсні для будь-яких умов польоту, які підпадають під припущення, зроблені при їх виведенні. Якщо у нас є Boeing 747, що летить під кутом атаки у вісім градусів і швидкістю 250 миль на годину, ці рівняння можна використовувати для пошуку дальності та витривалості, хоча це, очевидно, не оптимальна швидкість та кут атаки. Якщо ми хочемо визначити оптимальний діапазон або витривалість, ми повинні використовувати значення коефіцієнта підйому та опору, а також швидкість, яку ми виявили раніше, необхідні для цих оптимімумів.

Раніше ми з'ясували, що для максимальної витривалості літаку потрібно літати при мінімальних умовах опору. Наше фактичне рівняння витривалості підтверджує це, показуючи витривалість як функцію відношення коефіцієнта підйому до опору, яке буде максимальним, якщо опір буде мінімальним.

Ми також виявили, що діапазон буде оптимальним, якби опір, розділений на швидкість, був мінімальним. Кореляція між цією умовою та поведеними рівняннями діапазону не настільки очевидна, як співвідношення мінімального опору з рівнянням витривалості. Використання прямих і рівних відносин сили польоту, якими можна маніпулювати, щоб показати

Д = Ш [Д/Л] = Ш [С _{Д/С _Л]}

кількість V/D може бути записана

В/Д = [В/ Ш] [С _Л/С _Г].

Тепер використовуючи співвідношення швидкості для прямого та рівного польоту

$V = [2Вт/ (ρСКЛ)] 1/2$

знаходимо

$В/Д = [2Вт/ρ] 1/2 (1/Вт) (CL1/2/CD)$

Тому ми виявляємо, що максимальний діапазон виникає, коли для заданої ваги та висоти

C _L ^1/2 /C _D - максимум.

Якщо припустити параболічний опір полярний з постійними C, _D0 і K, ми можемо записати

С _Л ^1/2 /С _Д = С _Л ^1/2/[С _Д0 + КЦ _Л ²]

Щоб знайти, коли ця комбінація термінів на максимумі, ми можемо взяти її похідну щодо її змінної (C _L) і встановити її рівною нулю.

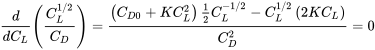
$ДДКл (CL1/2CD) = (СД0+ККЛ2) 12КЛ−1/2−КЛ1/2 (2ККЛ) СД2 = 0$

Рішення цього дає

½ (С _Д0 + КС _Л ²) С _Л ^1/2 — (2КЦ _Л ² )/С _Л ^1/2 = 0

або

С _Д0 + КС _Л ² -4КЦ _Л ² = 0

потім

С _Д0 = 3КК _Л ²

і, нарешті

С _Л = [С _Д0/3К] ^{^1/2}.

Таким чином, для максимальної дальності

$КЛМАХР=СД03К.$

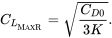
Використання цього в полярному опорі дає значення коефіцієнта опору для максимального діапазону.

C _Дмакс _Р = С _Д0 + КК _ЛМакср ² = С _Д0 + КК _Д0 /(3К) = (4/ 3) С _Д ₀.

Вони називаються умовами для «миттєвого» максимального діапазону. Термін миттєвий використовується, оскільки розрахунки призначені для заданої ваги, і ми знаємо, що вага змінюється під час польоту. Іншими словами, у будь-якій точці під час польоту, на вазі та висоті в цій точці коефіцієнти підйому та опору, знайдені вище, дадуть найкращий діапазон.

6.4 Діапазон і витривалість: Prop

Тепер ми розглянемо дальність і витривалість для літаків, керованих гвинтом, в яких продуктивність двигуна зазвичай виражається з точки зору потужності замість тяги. Дослідження дальності та витривалості для літаків, які мають продуктивність, виміряну з точки зору потужності (гвинтовий літак), проводиться шляхом визначення потужності питомої витрати палива, подібного до питомої витрати палива тяги, що використовується для струменів. Потужність питомої витрати палива визначається як маса палива, споживаного в одиницю часу на одиницю потужності вала. Одиниці - це слимаки на одиницю потужності в секунду в англійській системі або кілограм на одиницю потужності в секунду в одиницях СІ.

[C _p] = сл/(потужність-сек) або кг/ (потужність-сек)

Використовувані силові агрегати - це кінські сили в англійській системі і ват в одиницях СІ.

Так само, як ми це робили в реактивному (тяговому) випадку, ми часто знайдемо альтернативне визначення питомої витрати палива, наведене з точки зору ваги споживаного палива замість маси.

$γp=GCP [фунт-паливо/к.с. сек.]$

Хоча належною одиницею часу є секунди, ми часто знаходимо такі дані, наведені для двигуна в терміні годин. Ми будемо розробляти наші рівняння з точки зору фундаментальних одиниць (секунди для часу) і, як у випадку з струменем, припустимо «квазі-рівневий» політ, який має

P _{корисний} = P _req = DV

При роботі з опорними двигунами ми повинні враховувати коефіцієнт корисної дії, η _р, який пов'язує потужність валу, P _s, що надходить від самого двигуна до потужності, ефективно використовуваної опорою для передачі імпульс в повітря.

$Паваіл = DV=PPS$

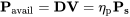
Що стосується струменя, то щоб знайти витривалість, ми повинні розглянути

$ДВФ/ДТ = γpps = γПДВ/P$

і для асортименту цікавляться

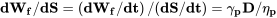
$ДВФ/ДС = (ДВФ/ДТ)/(ДС/ДТ) = γPD/P$

З наведених вище рівнянь очевидно, що при заданій питомій витраті палива і ККД норма використання палива мінімальна (миттєва витривалість - максимум), коли необхідна потужність (ДВ) мінімальна. Також очевидно, що витрата палива на кількість пройденої відстані є мінімальним (миттєвий діапазон - максимум), коли опір мінімальний.

Тому ми знову стикаємося з нашими старими друзями мінімальною необхідною потужністю і мінімальним перетягуванням, як умови, необхідні для оптимального польоту. Ми вже знаємо, як знайти їх графічно на графіках потужності та швидкості, як показано нижче. Це графічне визначення мінімальної потужності та мінімальної швидкості перетягування справедливо для будь-якого полярного опору, навіть якщо не параболічного.

Графік показує силовий ковпачок P на вертикальній осі, тоді як ковпачок швидкості V - горизонтальна вісь. Параболічна крива потужності показана аналогічно кривій перетягування на попередньому малюнку. Проводиться лінія дотичної до кривої, яка перетинається зі швидкістю для мінімального опору, ковпачок V sub cap M cap D. Мінімальна потужність відбувається при ковпачку V sub cap M cap P, внизу кривої потужності. — Малюнок 6.2: Швидкості для мінімальної потужності і перетягування

На цьому етапі ми повинні зробити паузу і сказати: «Гей, почекайте лише хвилину! Це було всього пару сторінок назад, що ви сказали, що максимальна витривалість відбулася при мінімальних умовах перетягування. Тепер ви говорите, що це максимальний діапазон, який я отримую при мінімальних умовах перетягування. Зробіть свій розум, заради Піта!»

Проблема в тому, що в одному випадку мова йде про реактивні літаки, а в іншому, опорні літаки. Це означає, що ми повинні бути дуже обережними, щоб побачити, з яким типом площини ми маємо справу, перш ніж починати будь-які розрахунки. Дуже легко потрапити в великий поспіх і отримати два випадки змішані (особливо в запалі бою на тесті або іспиті!).

Тепер, як ми зробили для реактивного літака, ми можемо розробити інтеграли для визначення дальності або витривалості для будь-якої ситуації польоту. Для витривалості у нас є

$е = Т1Т2ДТ = −W1W2PDWγPDV$

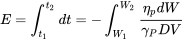
і для асортименту

$R = s1s2ds = −w1w2η пдвγpd$

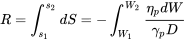
6.5 Приблизні рішення для дальності та витривалості для опорного літака

Ми ще раз припустимо «квазі-рівневий» політ і маніпулювати умовами наших відносин балансу сил, щоб дати

$D = W\left[\dfrac{D}{L}\right] = W\left[\dfrac{C_D}{C_L}\right]$

Це робить витривалість невід'ємною

$\mathrm{E}=-\int_{W_{1}}^{\mathrm{W} 2} \frac{\eta_{\mathrm{p}}}{\gamma_{\mathrm{p}}} \frac{1}{\mathrm{~V}} \frac{\mathrm{C}_{\mathrm{L}}}{\mathrm{C}_{\mathrm{D}}} \frac{\mathrm{d} \mathrm{W}}{\mathrm{W}}$

Використання прямого та рівного співвідношення швидкості

$\mathrm{V}=\left[2 \mathrm{~W} /\left(\rho \mathrm{SC}_{\mathrm{L}}\right)\right]^{1 / 2}$

отримуємо

$\mathbf{E}=-\int_{\mathbf{W} 1}^{\mathrm{W} 2} \frac{\eta_{\mathrm{p}}}{\gamma_{\mathrm{p}}}[\rho \mathrm{S} / 2]^{1 / 2} \frac{\mathrm{C}_{\mathrm{L}}^{3 / 2}}{\mathrm{C}_{\mathrm{D}}} \frac{\mathrm{dW}}{\mathrm{W}^{3 / 2}}$

Інтеграл діапазону можна записати аналогічним чином, як

$R=-\int_{W_{1}}^{W_{2}} \frac{\eta_{P}}{\gamma_{P}} \frac{C_{L}}{C_{D}} \frac{d W}{W}$

Тепер нам потрібно розглянути ті ж розклади польотів, розглянуті в реактивному випадку. Постійний кут польоту атаки дасть постійні коефіцієнти підйому і опору, а постійна висота дасть постійну щільність. Будемо також вважати постійну питому витрату палива.

Для дальності нам потрібно лише використовувати постійний кут атаки припущення, щоб дати простий інтеграл. Отриманий діапазон

$R=\frac{\eta_{P}}{\gamma_{P}} \frac{C_{L}}{C_{D}} \ln \left(\frac{W_{1}}{W_{2}}\right), \quad(\text { const } \alpha)$

Для витривалості розглянемо два випадки. Перший тримає як висоту, так і кут атаки постійними, даючи

$E=-\frac{\eta_{P}}{\gamma_{P}} \sqrt{\frac{\rho S}{2}} \frac{C_{L}^{3 / 2}}{C_{D}} \int_{W_{1}}^{W_{2}} \frac{d W}{W^{3 / 2}}$

який інтегрується в

\ [E=\ frac {\ eta_ {P}} {\ gamma_ {P}}\ sqrt {2\ rho S}\ frac {C_ {L} ^ {3/2}} {C_ {D}}\ ліворуч (\ frac {1} {Sqrt {W_ {2}}}} -\ frac {1} {\ sqrt {W_ {1}}}\ праворуч),\ лівий (\ begin {масив} {l}
\ текст {const}\ альфа\
\ текст {const}\ rho
\ end {масив}\ праворуч)\]

Другий випадок має кут атаки і постійну швидкості.

$E=-\frac{\eta_{P}}{\gamma_{P}} \frac{1}{V} \frac{C_{L}}{C_{D}} \int_{W_{1}}^{W_{2}} \frac{d W}{W}$

або

\ [E=\ розрив {\ eta_ {P}} {\ gamma_ {P}}\ frac {1} {V}\ frac {C_ {L}} {C_ {D}}\ ln\ лівий (\ frac {W_ {1}}} {W_ {2}}\ правий),\ квад\ лівий (\ почати {масив} {l}
\ text {cons st}\ альфа\
\ текст {const} V
\ end {масив}\ праворуч)\]

Це «дрейф вгору» розклад польотів.

6.6 Ефекти вітру

Вищевказані рівняння дальності та витривалості для обох реактивних або опорних літаків були отримані, припускаючи відсутність атмосферних вітрів. Швидкості в рівняннях - це повітряні швидкості, а не швидкості над землею. Якщо є вітер, швидкість повітря, звичайно, не дорівнює швидкості над землею.

Розрахунки витривалості не змінюються наявністю атмосферного вітру. Якщо наше занепокоєння полягає в тому, як довго літак може залишатися в повітрі на заданій швидкості та висоті, і ми не особливо дбаємо, якщо він прогресує над землею, нам не потрібно турбуватися про вітри. Ми проводимо розрахунки на витривалість, грунтуючись тільки на аеродинамічній поведінці літака при заданій швидкості і висоті в масі повітря.

Діапазон пов'язаний зі швидкістю через землю, а не швидкістю повітря; таким чином, якщо є вітер, наші результати рівняння дальності потрібно повторно оцінити, щоб врахувати вітер. Логіка цього проста: зустрічний вітер сповільнить прогрес над землею і зменшить дальність, тоді як попутний вітер збільшить дальність. Що не так очевидно, так це те, як виправити розрахунки, щоб врахувати цей вітер. Оскільки наша звичайна турбота полягає в тому, щоб знайти максимальну дальність, ми розглянемо корекцію впливу вітру тільки для цієї оптимальної ситуації.

Максимальний діапазон для струменя був виявлений, коли D/V був мінімальним, тоді як для опори максимальний діапазон відбувався при мінімальних умовах опору. Швидкості для обох випадків можна визначити графічно, знайшовши точку дотику для лінії, проведеної від початку нульової швидкості на кривій опори проти швидкості у випадку струменя або потужності, необхідної проти кривої швидкості для опорної площини. Ми можемо використовувати розширення цього графічного підходу, щоб знайти швидкість для найкращого діапазону з або зустрічним вітром, або хвостовим вітром.

Важливим першим кроком у визначенні оптимальної дальності при наявності атмосферного вітру є пошук нової швидкості польоту для найкращої дальності з вітром. Ця нова швидкість буде використана для обчислення нового значення оптимального діапазону. Нове значення найкращої дальності повітряної швидкості знайдено, як показано на малюнках нижче. Перше завдання полягає в тому, щоб намалювати звичайний опір проти швидкості (для струменя) або потужності, необхідної проти швидкості (для опори) ділянки. До цієї ділянки додається нове походження, зміщене вліво на значення попутного вітру або вправо на величину попутного вітру. Потім проводиться лінія від зміщеного початку, дотичної до кривої опору або потужності, а точка дотику визначає нову швидкість для оптимального діапазону з вітром. Величина цього нового оптимального діапазону швидкості зчитується відносно початкового походження (а не зміщеного походження). Ця швидкість - повітряна швидкість, а не наземна швидкість.

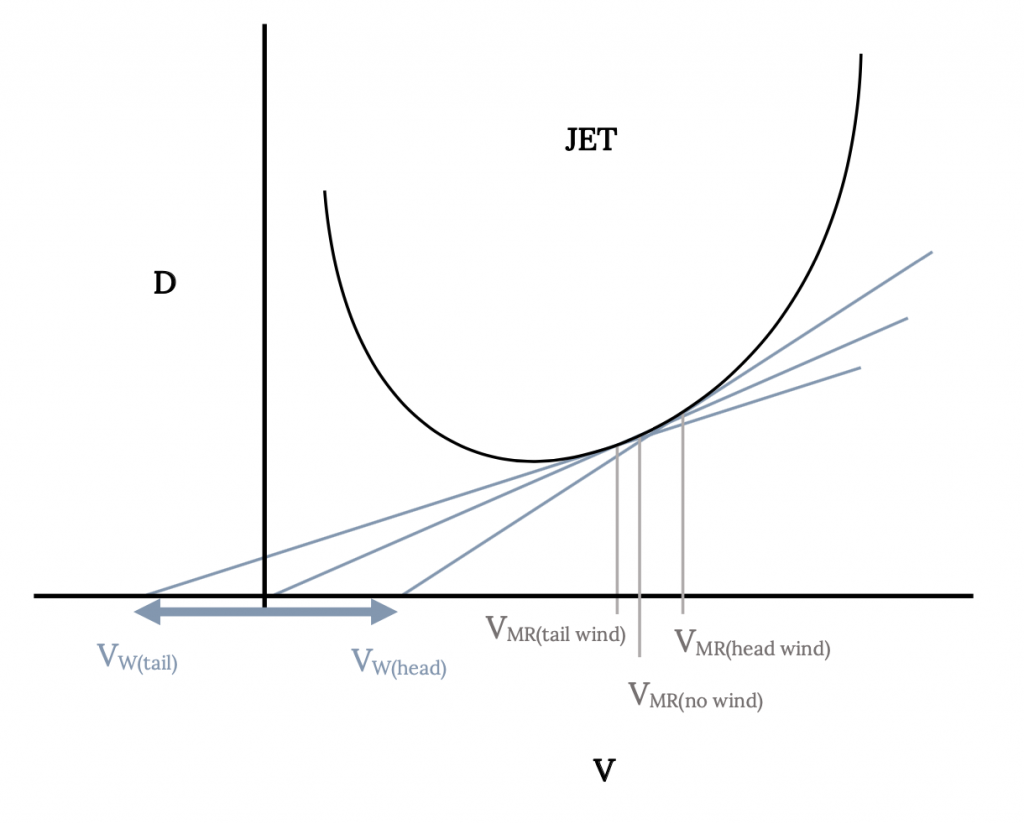
Такий же графік Cap D проти cap V для струменя показаний, як і раніше, але тепер з трьома дотичними лініями. Початкова лінія, що перетинає криву перетягування на ковпачку V sub cap M cap R, присутня. Показано другу лінію для хвостового вітру, яка починається з від'ємного значення V ковпачка, відповідного кришці V sub w хвоста, внаслідок чого вона перетинає криву перетягування на нижньому ковпачку V значення, позначене ковпачком V sub cap M cap R заднього вітру. Показано третю лінію для зустрічного вітру, яка починається з позитивного значення кришки V, відповідного головці ковпачка V sub w, в результаті чого вона перетинає криву перетягування при більш високому значенні кривого V, позначеного ковпачком V sub cap M cap R зустрічного вітру. — Малюнок 6.3: Швидкість для найкращого діапазону з вітром (Jet)

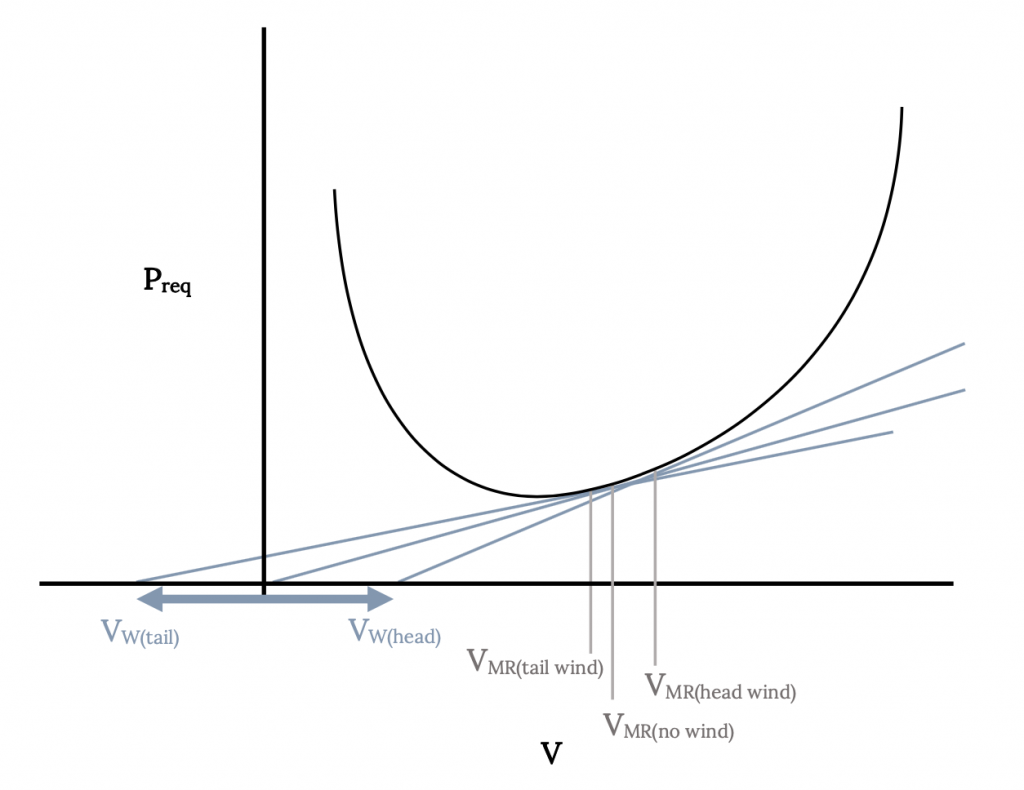
Показано сюжет, що нагадує попередній малюнок, але з необхідною потужністю ковпачок P sub req на вертикальній осі замість перетягування ковпачка D. Такі ж явища показані, з заднім вітром зміщення ковпачка V sub cap M cap R заднього вітру до меншого значення, і зворотного вітру зміщення ковпачка V sub cap M cap R зустрічного вітру до більш високого значення. — Малюнок 6.4: Швидкість для найкращого діапазону з вітром (Prop)

Потім ця нова оптимальна швидкість діапазону використовується для пошуку нового значення діапазону з тих же рівнянь, розроблених раніше. Використовуючи нову швидкість, спочатку обчислюються нові значення коефіцієнтів підйому та опору, і ці нові коефіцієнти та швидкість використовуються для пошуку оптимального діапазону з вітром. До цього нового діапазону слід додати ще один діапазон, який є результатом виключно від часу експозиції літака (витривалості) вітру. Ця витривалість також виявляється за допомогою недавно знайденої оптимальної швидкості діапазону та пов'язаних з ними коефіцієнтів. Остаточний коригований діапазон для максимальної дальності при вітрі

R _з _вітром = R _{Виправлено} + V _w E _{Виправлено} для попутного вітру

або

R _з _вітром = R _{Виправлено} — V _w E _{Виправлено} для зустрічного вітру

6.7 Нехай покупець остерігається

Виробники літаків, як і автомобілі та інші продукти, люблять робити все можливе, щоб їх продукт виглядав добре, і іноді вони сподіваються, що покупець не надто уважно дивиться на суперечності в їх специфікаціях і рекламі. Автомобіль може бути рекламований як сидіння для п'яти, рейтинг економії палива EPA 38 миль на галон, можливість їхати 542 миль на один бак газу і максимальна швидкість 120 миль на годину. Більшість з нас, однак, знають, що не варто очікувати, що автомобіль проїде 542 миль на одному резервуарі з газом, перевозячи 5 людей зі швидкістю 120 миль/год! Ті, хто вважає, що це також, ймовірно, буде досить німим, щоб заплатити ціну наклейки.

А як щодо літаків? Чи є цей продукт галузі, яка регулюється на кожному кроці FAA так само, як і суперечності в технічних характеристиках, як автомобіль?

Давайте розглянемо кілька простих прикладів, взятих з каталогу авіаційного флоту загальної авіації кілька років тому. A Cessna 150, найбільш широко використовуваний два місця літаків в країні, цитує діапазон 815 морських миль на 32 галонів (210 фунтів) палива. Літак має порожню вагу (без пілота, пасажира, багажу чи палива) 1104 фунтів і максимальну злітну вагу 1600 фунтів. Це означає, що з повними паливними баками, необхідними для максимального діапазону, є лише 286 фунтів надбавки як для пілота, так і для пасажирів, навряд чи достатньо для двох дорослих та багажу! Ось чому одне з улюблених питань льотних екзаменаторів, які готуються до приватного пілота чек-їзди в Cessna 150 включає вагу та баланс літака, і чому іноді пілотам, можливо, доведеться фактично викачувати паливо з літака перед зльотом.

A Cessna 172, найпопулярніший чотиримісний літак у світі, трохи краще, ніж 150, наведені вище. Він має порожню вагу 1387 фунтів і досягти рекламованого діапазону 742 миль він має паливний бак, який вміщує 288 фунтів газу. Це дає загальну вагу для літака і палива 1675 фунтів. Максимальна вага брутто зльоту 172 2300 фунтів, залишаючи 625 фунтів надбавки для чотирьох пасажирів і їх речі; в середньому 156 фунтів кожен! Він починає виглядати, як літаки розроблені як ті «чотиримісні» автомобілі, які мають заднє сидіння приблизно досить велике, щоб вмістити двох маленьких пуделів!

З іншим продуктом Cessna, все навколо найкраще з їх лінійки сидінь 4, Skylane, справи трохи краще. Його перерахована порожня вага 1707 фунтів, діапазон 979 морських миль на 474 фунтів палива і максимальна вага брутто 2950 фунтів залишають 769 фунтів для пілота, пасажирів та аксесуарів (192 фунтів кожен). Нарешті літак для реальних людей!

Щоб наївним не прийшла думка, що це тільки проблема для невеликих одномоторних літаків, давайте розглянемо ще один приклад, вісім місце Learjet 25C. Він стверджує, що діапазон 2472 миль, просто квиток для багатого молодого бізнес-магната, щоб заповнити сімома її найближчими друзями для трансконтинентального уїк-енду. Перерахована паливна ємність 7393 фунтів, додає до котирується «нульового палива» вага 11,400 фунтів, щоб дати 18 793 фунтів літака. Так скільки залишилося для тих 8 пасажирів? Перерахована максимальна вага брутто Learjet 25C становить 15 000 фунтів! При повному баку газу літак перевищує максимально допустиму злітну масу! З пілотом 160 фунтів і ніяких інших пасажирів або корисного навантаження цей літак може перевозити достатньо палива для реального діапазону близько 1150 миль, менше половини, що рекламується. Навіщо претендувати на дальність майже 2500 миль? Ну, паливні баки досить великі, щоб перевозити необхідне паливо. Якби тільки літак міг зійти з землі!

Домашнє завдання 6

1. Літак важить 56,000 фунтів і має 900 футів ² крила. Його полярне рівняння опору задається C _D = 0,016 + 0,04C _L ². Літак має турбореактивний двигун з постійною тягою на будь-якій заданій висоті, як показано нижче:

Таблиця 6.1: Питання 1

висота (фути)	0	5000	10 000	15 000	20 000	25 000	30 000
тяга (фунт)	6420	5810	5200	4590	4000	3360	2700

a. знайти мінімальну тягу, необхідну для прямого і рівного польоту, і відповідні справжні швидкості повітря на рівні моря і на 30000 футів.

b. знайти мінімальну необхідну потужність і відповідні справжні повітряні швидкості на рівні моря і 30000 футів.

2. Для літака вище:

a. сюжет тяги і перетягування проти V _e для прямого і рівневого польоту.

Графік показаний з перетягуванням і тягою з кроком у тисячу фунтів на вертикальній осі та ковпачком швидкості V з кроком 100 футів в секунду на горизонтальній осі. Вертикальна вісь йде від 0 до 7 тисяч, тоді як горизонтальна - від 0 до 600. — Малюнок 6.5: Тяга та перетягування проти V _e для прямого та рівного польоту

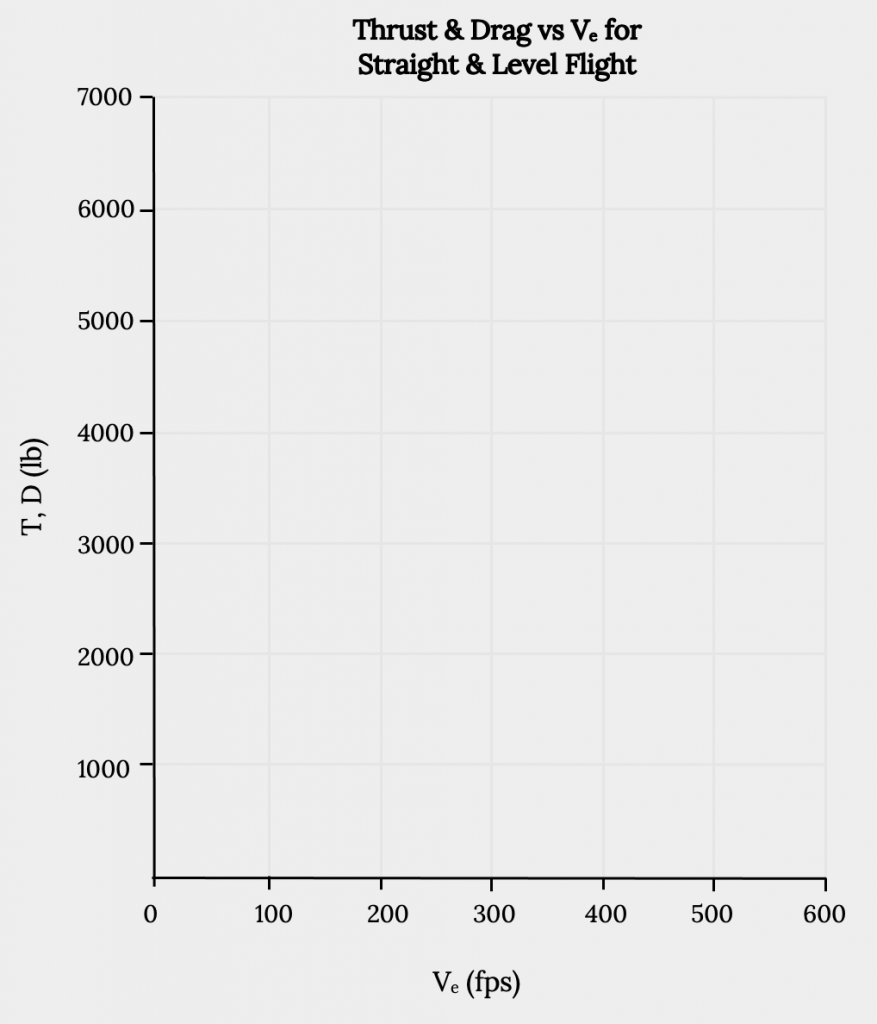
b. висота ділянки проти V _emax і V _max для прямого і рівневого польоту.

Сюжет показує висоту h у футах, з кроком 5 тисяч футів між 0 і 30 тисячами футів на вертикальній осі. Горизонтальна вісь - це ковпачок швидкості V або еквівалентний ковпачок швидкості V sub e в футах в секунду, зі зміщеним початком, починаючи з 200, а потім просувається з кроком від 100 до 800 футів в секунду. Кола представляють ковпачок V sub e, тоді як трикутники представляють шапку V sub true.

Малюнок 6.6: Максимальна (і хв) швидкість для прямого та рівного польоту проти висоти

c. знайти висоту для максимальної істинної швидкості повітря.

d. знайти максимально досяжну висоту.

e. порівняйте V при мінімальному перетягуванні з графіка і розрахунку.

f. обчислити (L/D) _макс.

Посилання

Малюнок 6.1: Родинний сірий (2021). «Пошук швидкості для максимального діапазону». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/6.1-updated

Малюнок 6.2: Родинний сірий (2021). «Швидкості для мінімальної потужності і перетягування». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/6.2-updated

Малюнок 6.3: Родинний сірий (2021). «Швидкість для найкращого діапазону з вітром (Jet)». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/6.3-updated

Малюнок 6.4: Родинний сірий (2021). «Швидкість для найкращого діапазону з вітром (Prop)». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/6.4-updated

Малюнок 6.5: Родинний сірий (2021). «Тяга і перетягнути проти V_e для прямого і рівного польоту.» CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/hw-6-part-1

Малюнок 6.6: Родинний сірий (2021). «Максимальна (і мінімальна) швидкість для прямого та рівного польоту проти висоти». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/hw-6-part-2

Термін «аероплан» спочатку позначав крило, геометрично плоска поверхня, призначена для підтримки транспортного засобу в польоті по повітрю. До 1903 року термін став асоціюватися з усім літальним апаратом. До 1920-х років американська преса та журнали змінили слово на «літаки»; однак у Британії все ще прийнято бачити «літак», який використовується в книгах та паперах. ⁄2

<! — pb_fixme —><! — pb_fixme —>