4: Продуктивність у прямому та рівному польоті
- Page ID
- 28690
Вступ
Тепер, коли ми розглянули походження сил, які діють на літак в атмосфері, нам потрібно почати вивчати спосіб взаємодії цих сил, щоб визначити продуктивність транспортного засобу. Ми знаємо, що сили залежать від таких речей, як атмосферний тиск, щільність, температура та в'язкість у комбінаціях, які стають «параметрами подібності», такими як число Рейнольдса та число Маха. Ми також знаємо, що ці параметри будуть змінюватися як функції висоти в атмосфері, і у нас є модель стандартної атмосфери для опису цих варіацій. Також очевидно, що сили на літаку будуть функціями швидкості, і що це частина як числа Рейнольдса, так і числа Маха.
Багато питань, які ми матимемо щодо продуктивності літаків, пов'язані зі швидкістю. Як швидко може літати літак або як повільно він може йти? Як швидко може піднятися літак? Яка швидкість необхідна для зльоту зі злітно-посадкової смуги?
У попередньому розділі, присвяченому розмірному аналізу та подібності потоку, ми виявили, що сили на літаку є не лише функціями швидкості, а комбінацією швидкості та щільності, яка діє як тиск, який ми називали динамічним тиском. Ця комбінація з'являється як одне з трьох членів у рівнянні Бернуллі.
\[P+\frac{1}{2} \rho V^{2}=P_{0}\]
які можуть бути перебудовані для вирішення швидкості
\[V=\sqrt{2\left(P_{0}-P\right) / \rho}\]
У другій главі ми дізналися, як статичну трубку Піто можна використовувати для вимірювання різниці між статичним і загальним тиском, щоб знайти швидкість повітря, якщо щільність відома або передбачена. Ми обговорювали як еквівалентну швидкість повітря на рівні моря, яка передбачає стандартну щільність рівня моря при знаходженні швидкості, так і справжню швидкість польоту, яка використовує фактичну щільність атмосфери. При роботі з літальними апаратами прийнято називати еквівалентну повітряну швидкість на рівні моря як вказану швидкість польоту, якщо будь-яку помилку калібрування або розміщення приладу можна знехтувати. У цьому тексті ми припустимо, що такими помилками дійсно можна знехтувати, і термін, зазначений повітряна швидкість, буде використовуватися як взаємозамінний з еквівалентною повітряною швидкістю на рівні моря.
\[V_{I N D}=V_{e}=V_{S L}=\sqrt{\frac{2\left(P_{0}-P\right)}{\rho_{S L}}}\]
Слід зазначити, що наведені вище рівняння припускають нестисливий потік і не є точними при швидкостях, де ефекти стисливості значні. Теоретично ефекти стисливості повинні розглядатися при числах Маха вище 0,3; однак насправді вищевказані рівняння можуть бути використані без значної похибки до чисел Маха від 0,6 до 0,7.
Система індикації швидкості повітря високошвидкісних літаків повинна бути відкалібрована на більш складній основі, яка включає швидкість звуку:
\[V_{\mathrm{IND}}=\sqrt{\frac{2 a_{S L}^{2}}{\gamma-1}\left[\left(\frac{P_{0}-P}{\rho_{S L}}+1\right)^{\frac{\gamma-1}{\gamma}}-1\right]}\]
де\(a_{sl}\) = швидкість звуку на рівні моря і ρ SL = тиск на рівні моря. Гамма - це співвідношення питомих тепловитрат (Cp/Cv) для повітря.
Дуже високошвидкісний літак також буде оснащений індикатором Маха, оскільки число Маха є більш релевантною мірою швидкості літака при і вище швидкості звуку.
В іншій частині цього тексту буде припущено, що ефекти стисливості незначні, і нестислива форма рівнянь може бути використана для всіх обчислень, пов'язаних зі швидкістю. Зазначена швидкість польоту (швидкість, яку буде зчитувати пілот літака з індикатора повітряної швидкості) буде прийнята рівною рівню моря, еквівалентної швидкості повітряної швидкості. Таким чином, справжню швидкість повітря можна знайти, виправляючи різницю в рівні моря і фактичну щільність. Корекція заснована на знаннях, що відповідний динамічний тиск на висоті буде дорівнює динамічному тиску на рівні моря, що виявляється з еквівалентної швидкості повітря на рівні моря:
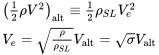
Важливим результатом цієї еквівалентності є те, що, оскільки сили на літаку залежать від динамічного тиску, а не швидкості польоту, якщо ми знаємо еквівалентні умови польоту на рівні моря та обчислюємо сили з цих умов, ці сили (а отже, і продуктивність літака) будуть правильно прогнозується на основі зазначених умов швидкості польоту і рівня моря. Це також означає, що пілоту літака не потрібно постійно перетворювати зазначені показання швидкості повітря в справжні швидкості повітря, щоб оцінити продуктивність літака. Літак завжди буде вести себе однаково при однаковій зазначеній швидкості повітря незалежно від висоти (в межах припущення про нестисливому потоці). Це особливо приємно знати в ситуаціях зльоту і посадки!
4.1 Статичний баланс сил
Багато з важливих експлуатаційних параметрів літака можуть бути визначені за допомогою тільки статики; тобто, припускаючи політ в рівноважному стані таким, щоб не було прискорень. Це означає, що політ знаходиться на постійній висоті без прискорення або уповільнення. Це дає загальне розташування сил, показане нижче.
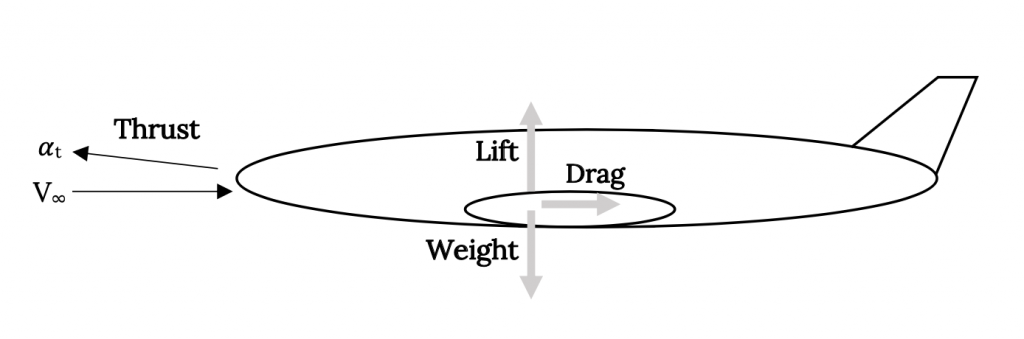
У цьому тексті ми розглянемо найпростіший випадок, коли тяга вирівнюється з вектором швидкості літака. Ми також зазвичай припустимо, що вектор швидкості вирівнюється з напрямком польоту або траєкторією польоту. Для цього самого основного випадку рівняннями руху стають:
Т — Д = 0
Л — Ш = 0
Зверніть увагу, що це узгоджується з визначенням підйому та опору як перпендикулярних та паралельних вектору швидкості або відносному вітру.
Тепер зробимо просте, але дуже основне припущення, що в прямому і рівному польоті підйом дорівнює вазі,
Л = Ш
Ми будемо використовувати це так часто, що буде легко забути, що це дійсно припускає, що політ дійсно прямий і рівний. Пізніше ми трохи обдуримо і використаємо це в неглибоких підйомах і ковзаннях, прикриваючи себе, припускаючи «квазі-прямий і рівний» політ. У заключній частині цього тексту ми нарешті вийдемо за рамки цього припущення, коли розглянемо поворот польоту.
Використання визначення коефіцієнта підйому
\[C_{L}=\frac{L}{\frac{1}{2} \rho V_{\infty}^{2} S}\]
і припущення, що підйом дорівнює вазі, швидкість в прямому і рівному польоті стає:
\[V=\sqrt{\frac{2 W}{\rho S C_{L}}}\]
Тяга, необхідна для підтримки цієї швидкості в прямому і рівному польоті, також є функцією ваги літака. Так як T = D і L = W ми можемо записати
Д/Л = Т/Ш
або
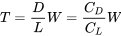
Тому для прямого та рівного польоту ми знаходимо таке співвідношення між тягою та вагою:
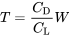
Наведені вище рівняння для тяги і швидкості стають нашими першими дуже основними відносинами, які можуть бути використані для встановлення продуктивності літака.
4.2 Аеродинамічний стійло
Раніше ми обговорювали аеродинамічний стійло. Для аеропрофілю (2‑D) або крила (3‑D) при збільшенні кута атаки досягається точка, де зменшується збільшення коефіцієнта підйому, що супроводжує збільшення кута атаки. Коли це відбувається, коефіцієнт підйому проти кута атаки стає нелінійним, оскільки потік над верхньою поверхнею крила починає відриватися від поверхні. Це поділ потоку може бути поступовим, як правило, прогресуючи від кормового краю аерокрила або крила і рухається вперед; раптовим, оскільки потік відривається від великих частин крила одночасно; або деяка комбінація двох. Фактичний характер стійла буде залежати від форми перерізу аерокрила, форми крила та числа Рейнольдса потоку.
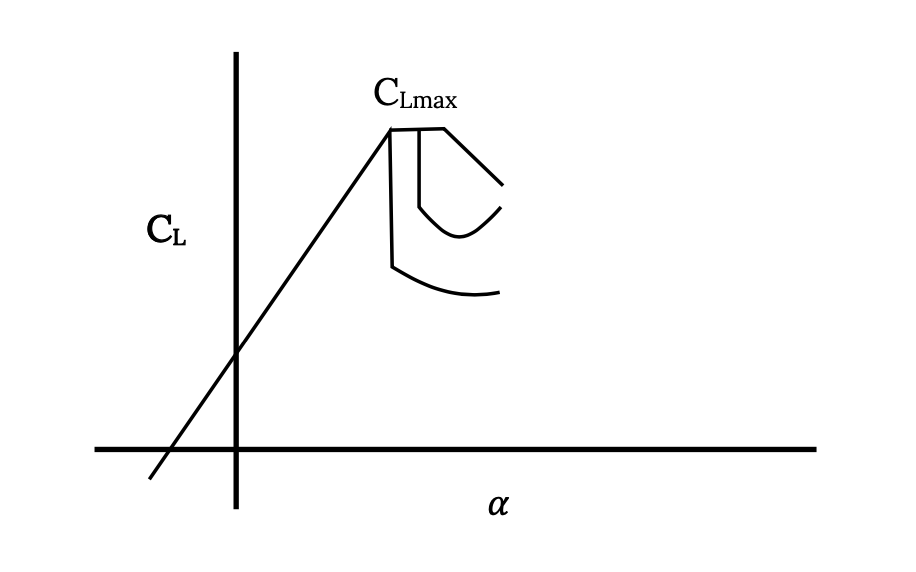
Ми визначаємо кут нахилу атаки як кут, де коефіцієнт підйому досягає максимуму, CLmax, і використовуємо це значення коефіцієнта підйому для розрахунку швидкості стійла для прямого та рівного польоту.
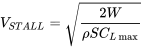
Зверніть увагу, що швидкість стійла буде залежати від ряду факторів, включаючи висоту. Якщо ми подивимось на рівню моря, еквівалентну швидкості стійла, ми маємо
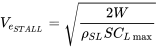
Слід підкреслити, що швидкість стійла, як визначено вище, базується на підйомі, рівному вазі або прямому та рівному польоті. Це швидкість стійла, вказана у всіх посібниках з експлуатації літаків і використовується як орієнтир пілотами. Потрібно пам'ятати, що стійло є лише функцією кута атаки і може відбуватися на будь-якій швидкості. Визначення швидкості стійла, що використовується вище, є результатом обмеження польоту до прямих і рівних умов, де підйом дорівнює вазі. Ця швидкість стійла не застосовується для інших умов польоту. Наприклад, в повороті підйомник буде нормально перевищувати вагу, а затримка буде відбуватися з більшою швидкістю польоту. Те ж саме стосується прискорених умов польоту, таких як підйом. З цієї причини пілотів навчають обробляти стійло в сходження і повороту польоту, а також у прямому і рівному польоті.
Для більшої частини цього тексту ми будемо мати справу з польотом, який передбачається прямим і рівним, і тому будемо вважати, що пряма і рівна швидкість стійла, показана вище, є актуальною. Ця швидкість зазвичай представляє найнижчу практичну пряму та рівну швидкість польоту для літака і, таким чином, є важливим параметром продуктивності літака.
Зазвичай ми визначаємо швидкість стійла для літака з точки зору максимальної ваги брутто зльоту, але слід зазначити, що вага будь-якого літака буде змінюватися в польоті, оскільки використовується паливо. Для заданої висоти, коли вага змінюється, зміна швидкості стійла з вагою можна знайти наступним чином:
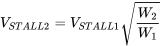
Очевидно, що в міру просування польоту і зменшення ваги літака зменшується і швидкість стійла. Оскільки швидкість зупинки являє собою нижню межу прямої та рівної швидкості польоту, це свідчить про те, що літак зазвичай може приземлитися з меншою швидкістю, ніж мінімальна швидкість зльоту.
Для багатьох великих транспортних літаків швидкість стійла повністю завантаженого літака занадто висока, щоб забезпечити безпечну посадку на тій же відстані, яка необхідна для зльоту. У випадках, коли літак повинен повернутися на своє злітне поле для посадки через якусь надзвичайну ситуацію (наприклад, відмова шасі втягнути), він повинен скинути або спалити паливо перед посадкою, щоб зменшити його вагу, швидкість затримки та швидкість посадки. Зліт і посадка будуть розглянуті в наступному розділі набагато докладніше.
4.3 Перспективи на стійло
Під час обговорення стійла варто розглянути деякі фізичні аспекти стійла та багато помилок, які є як пілоти, так і громадськість щодо стійла.
Для аерокосмічного інженера, стійло C Lmax, найвища можлива підйомна здатність літака; але, для більшості пілотів та громадськості, стійло - це місце, де літак втрачає весь ліфт! Як це може бути і те, і інше? І, якщо один з цих поглядів помилковий, чому?
Ключем до розуміння обох перспектив стійла є розуміння різниці між підйомним і підйомним коефіцієнтом. Підйом - це твір коефіцієнта підйому, динамічного тиску та площі форми крила. Для заданої висоти та літака (площі крила) підйом залежить від коефіцієнта підйому та швидкості. Можливий дуже високий коефіцієнт підйому C L і дуже низький підйом, якщо швидкість низька.
Коли літак знаходиться під кутом атаки таким, що досягається C Lmax, високий кут атаки також призводить до високого коефіцієнта опору. В результаті високий опір зазвичай призводить до зниження швидкості повітря, що потім призводить до втрати ліфта. У традиційно розробленому літаку це буде супроводжуватися краплею носа літака в ніс вниз ставлення і втрата висоти, оскільки швидкість відновлюється і піднімається. Якщо пілот намагається утримувати ніс літака вгору, літак просто впаде в ніс вгору ставлення. Пілотів навчають пускати ніс краплі, як тільки вони відчувають затримку, так що підйом і відновлення висоти може початися якомога швидше. Хороший інструктор польоту навчить пілота відчувати стійло при його настанні таким чином, що відновлення може початися до висоти і підйому втрачається.
Слід зазначити, що якщо літак має достатню потужність або тягу, а високий опір, присутній на C Lmax, може відповідати тязі, політ може бути продовжений в стійло і після стійла області. Це можливо на багатьох винищувальних літаках, і царство польоту після стійла пропонує багато цікавих можливостей для маневру в «собачий бій».
Широка громадськість схильна думати про стійло, як коли літак падає з неба. Це можна побачити практично в будь-якому газетному повідомленні про аварію літака, де сюжетна лінія буде звучати «літак заглох і впав з неба, носом занурюючись в землю після того, як двигун вийшов з ладу». Цей вид звіту має кілька помилок. Стійка не має нічого спільного з двигунами і втрата двигуна не викликає затримки. Вітрильники можуть зупинятися, не маючи двигуна, і кожного пілота навчають, як літати на літаку до безпечної посадки, коли двигун втрачається. Зрив також не змушує літак піти в занурення. Однак пілот може панікувати при втраті двигуна, ненавмисно увійти в стійло, не вжити належних дій з відновлення стійла і, можливо, «занурення в ніс» в землю.
4.4 Потрібен перетягування та тяга
Як видно вище, для прямого і рівного польоту тяга повинна дорівнювати перетягуванню. Перетягування - це функція коефіцієнта опору C D, який, в свою чергу, є функцією опорного опору та індукованого опору.
С Д = С Д0 + С Ді
Припускаємо, що цей зв'язок має параболічну форму і що індукований коефіцієнт опору має вигляд
С Ді = КЦ Л 2
Тому пишемо
С Д = С Д0 + КС Л 2
З нечіткої аеродинамічної теорії виявлено, що K є функцією співвідношення сторін і плоскоподібної форми крила.

де e - одиниця для ідеальної еліптичної форми розподілу підйому вздовж прольоту крила і менше одиниці для неідеальних розподілів підйому.
Показане вище співвідношення коефіцієнта опору називається параболічним опором «полярним» через його математичну форму. Насправді це справедливо лише для нев'язливої теорії крила, а не для всього літака. У цьому тексті ми будемо використовувати це рівняння як перше наближення до поведінки перетягування всього літака. Хоча це лише наближення, це досить хороший для вступного курсу продуктивності рівня. Однак це може призвести до деяких нереалістичних оцінок продуктивності при використанні з деякими реальними даними літаків.
Опір літака знаходять з коефіцієнта опору, динамічного тиску та площі форми крила:
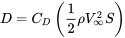
Тому
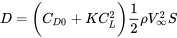
Розуміючи, що для прямого і рівного польоту підйом дорівнює вазі, а підйом - функція коефіцієнта підйому крила, ми можемо написати:
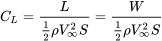
даруючи:
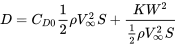
Вищевказане рівняння справедливо лише для прямого та рівного польоту для літака в нестисливому потоці з параболічним опором полярним.
Давайте розглянемо форму цього рівняння і розглянемо його фізичний сенс. Для даного літака на заданій висоті більшість членів у рівнянні є константами, і ми можемо записати
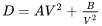
де
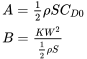
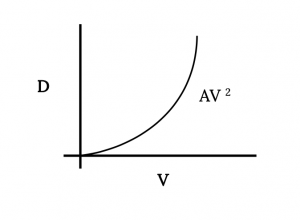
Перший член рівняння показує, що частина опору збільшується з квадратом швидкості. Це базовий термін перетягування, і логічно, що для основної форми літака опір буде збільшуватися зі збільшенням динамічного тиску. Для більшості спостерігачів це дещо інтуїтивно зрозуміло.
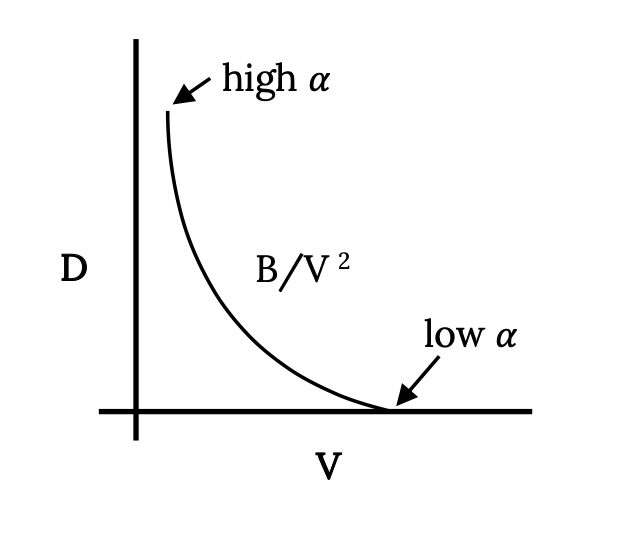
Другий член являє собою перетягування, яке зменшується зі збільшенням квадрата швидкості. Це дає нескінченне опір з нульовою швидкістю, однак, це недосяжна межа для нормально визначеного, фіксованого крила (на відміну від вертикального підйому) літаків. Слід зазначити, що цей термін включає в себе вплив коефіцієнта підйому або підйому на опору. Чим швидше літальний апарат літає, тим нижче значення коефіцієнта підйому, необхідного для того, щоб дати підйом рівний вазі. Коефіцієнт підйому, нагадаємо, є лінійною функцією кута атаки (до стійла). Якщо літак летить прямо і рівно, а пілот підтримує рівень польоту при зниженні швидкості літака, кут крила атаки повинен збільшуватися, щоб забезпечити коефіцієнт підйому і підйом, необхідний для того, щоб дорівнювати вазі. Зі збільшенням кута атаки дещо інтуїтивно, що опір крила збільшиться. Оскільки швидкість зменшується під час прямого та рівного польоту, ця частина опору продовжуватиме збільшуватися експоненціально, поки швидкість стійла не буде досягнута.
Додавання двох термінів перетягування разом дає наступний малюнок, який показує повну варіацію перетягування зі швидкістю для літака з параболічним перетягуванням полярним у прямому та рівному польоті.
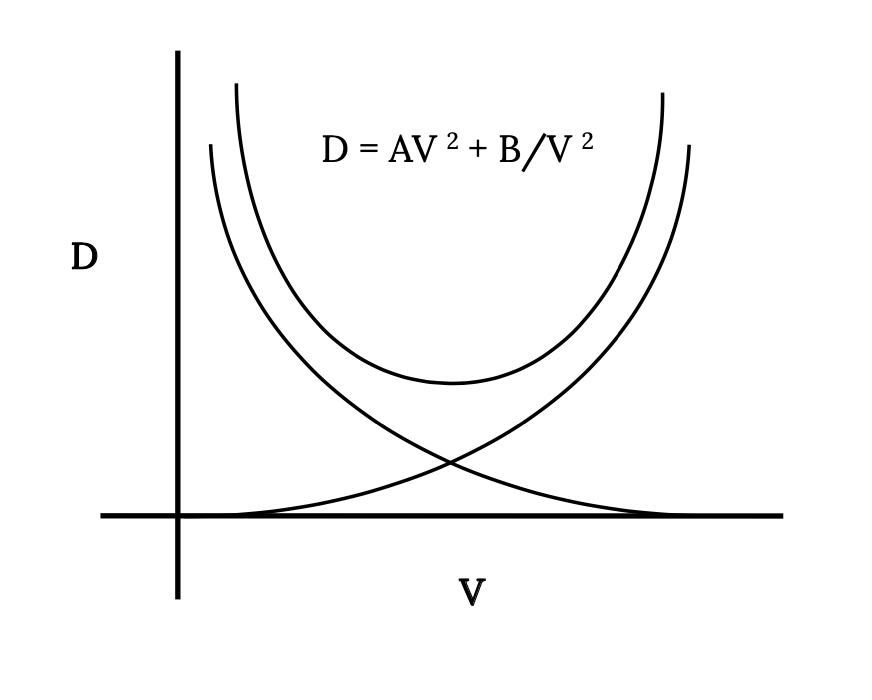
4.5 Мінімальне перетягування
Однією з очевидних точок інтересу на попередньому графіку перетягування є швидкість мінімального опору. Це, звичайно, можна знайти графічно з сюжету. Ми також можемо просто поглянути на рівняння, щоб знайти деяку іншу інформацію про умови мінімального опору.
Вимоги до мінімального опору інтуїтивно цікавлять, оскільки здається, що вони повинні певним чином стосуватися економіки польоту. Пізніше ми виявимо, що існують певні оптимальні показники, які залежать безпосередньо від польоту при мінімальних умовах опору.
На даний момент ми говоримо про знаходження швидкості, з якою літак летить при мінімальних умовах опору в прямому та рівному польоті. Важливо пам'ятати про це припущення. Пізніше ми виявимо, що певні оптими підйому та ковзання відбуваються в цих же умовах, і ми розтягнемо наше пряме та рівне припущення до одного з «квазі» -рівня польоту.
Ми можемо почати з дуже простого погляду на те, що наш ліфт, перетягування, тяга і вага баланси для прямого і рівневого польоту говорить нам про мінімальні умови опору, а потім ми перейдемо до більш складного погляду на те, як залежні від форми крила терміни в полярному рівнянні перетягування (CD0 і K) пов'язані як мінімум стан перетягування. Зрештою, найважливіше, що потрібно визначити - це швидкість польоту при мінімальному опорі, оскільки пілот може потім використовувати це, щоб літати при мінімальних умовах опору.
Давайте розглянемо наші прості відносини статичної сили:
Л = Ш, Т = Д
написати
Д = Ш х Д/Л
який говорить про те, що мінімальний опір виникає, коли опір, розділений на підйомник, є мінімальним або, навпаки, коли підйом розділений на опір є максимальним.
Ця комбінація параметрів, L/D, зустрічається часто при погляді на продуктивність літака. Загалом, як правило, інтуїтивно зрозуміло, що чим вище підйомник і чим нижче опір, тим краще літак. Не настільки інтуїтивно зрозуміло, що максимальне співвідношення ліфт-перетягування відбувається за тих самих умов польоту, що й мінімальне перетягування. Цей простий аналіз, однак, показує, що
МІНІМАЛЬНИЙ ОПІР ВИНИКАЄ, КОЛИ L/D МАКСИМАЛЬНИЙ.
Зверніть увагу, що оскільки C L/C D = L/D ми також можемо сказати, що мінімальний опір виникає, коли C L/C D є максимальним. Дуже важливо відзначити, що мінімальний опір не означає мінімальний коефіцієнт опору.
Мінімальний опір відбувається при одному значенні кута атаки, де коефіцієнт підйому, ділений на коефіцієнт опору, є максимальним:
D хв відбувається, коли (C L/C D) макс
Як зазначалося вище, це не під тим кутом атаки, при якому C D знаходиться на мінімумі. Це також не той кут атаки, де коефіцієнт підйому максимальний. Це повинно бути досить очевидним, оскільки C Lmax відбувається на стійлі, а опір дуже високий на стійлі.
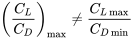
Оскільки мінімальний опір є функцією лише співвідношення коефіцієнтів підйому та опору, а не висоти (щільності), фактичне значення мінімального опору для даного літака при заданій вазі буде інваріантним з висотою. Фактична швидкість, з якою відбувається мінімальний опір, є функцією висоти і, як правило, збільшуватиметься зі збільшенням висоти.
Якщо припустити параболічний опір полярним і побудувати рівняння перетягування
для перетягування проти швидкості на різних висотах отримані криві виглядатимуть приблизно так:
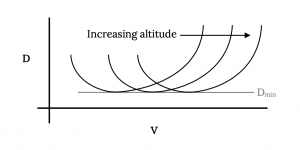
Зауважте, що мінімальний опір буде однаковим на кожній висоті, як зазначено раніше, а швидкість мінімального опору збільшуватиметься з висотою.
Ми обговорювали в попередньому розділі той факт, що через взаємозв'язок між динамічним тиском на рівні моря з тим, що на висоті, літак завжди буде виконувати те ж саме при тій же зазначеній або еквівалентній швидкості повітря на рівні моря. Дійсно, якщо записати рівняння перетягування як функцію щільності рівня моря та еквівалентної швидкості рівня моря, вийде одна крива.
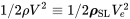
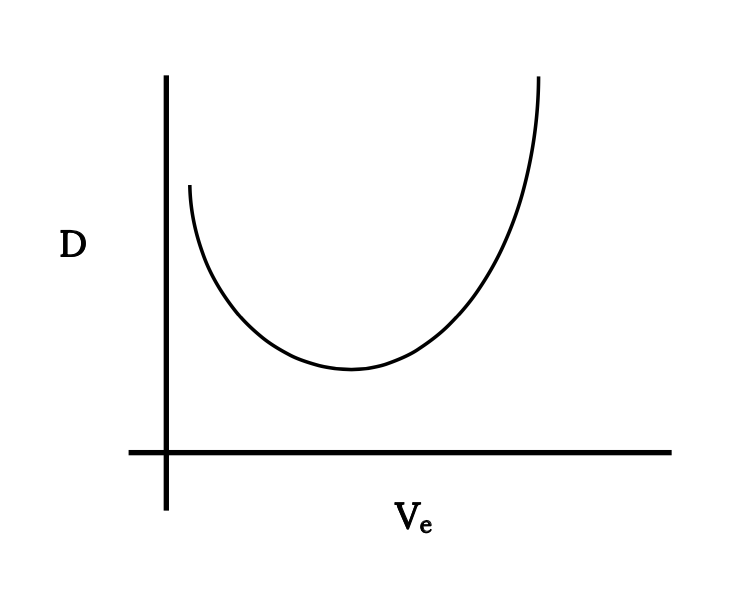
Щоб знайти поведінку опору проти швидкості літака, тоді необхідно лише зробити розрахунки або графіки в умовах рівня моря, а потім перетворити на справжню швидкість польоту на будь-якій висоті, використовуючи співвідношення швидкості нижче.
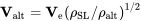
4.6 Мінімальний підсумок перетягування
Ми знаємо, що мінімальний опір виникає, коли коефіцієнт підйому до перетягування знаходиться на максимумі, але коли це відбувається; при якому значенні C L або C D або з якою швидкістю?
Один із способів знайти C L і C D при мінімальному перетягуванні - це побудувати один проти іншого, як показано нижче. Максимальне значення відношення коефіцієнта підйому до коефіцієнта опору буде там, де лінія від початку початку просто дотична до кривої торкнеться кривої. У цьому пункті знаходяться значення C L і C D для мінімального опору. Цей графічний метод знаходження мінімальних параметрів опору працює для будь-якого літального апарату, навіть якщо він не має параболічного опору полярного.
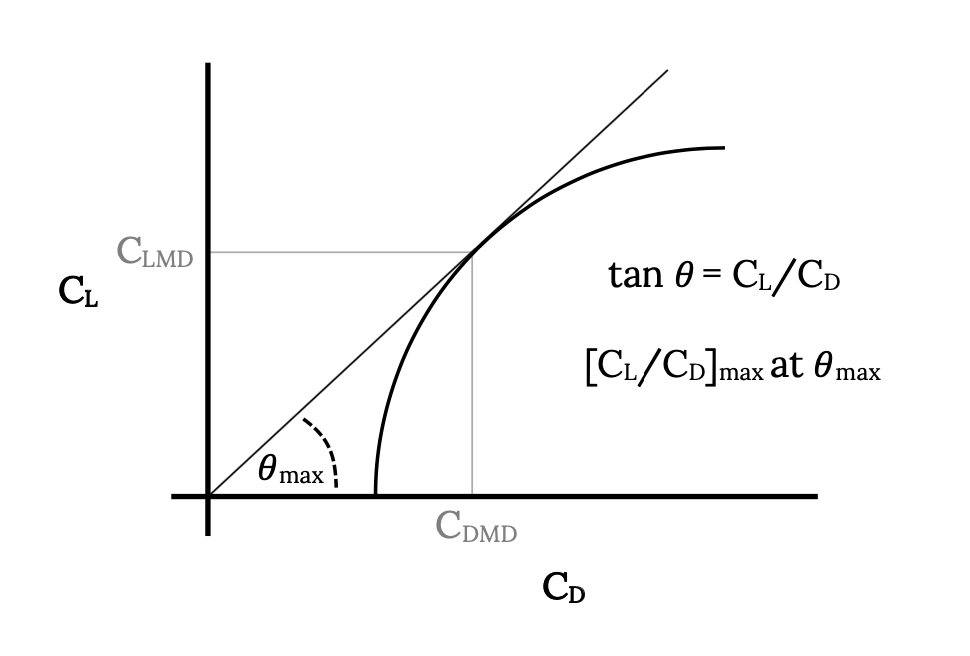
Після того, як C Lmd і C Dmd знайдені, швидкість для мінімального опору знаходиться з рівняння нижче, за умови, що літак знаходиться в прямому і рівному польоті
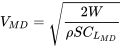
Як ми вже знаємо, швидкість мінімального опору можна знайти для умов рівня моря (еквівалентна швидкості рівня моря) і з цього легко знайти мінімальну швидкість опору на висоті.
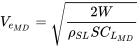
Слід також зазначити, що коли відомі коефіцієнти підйому і опору для мінімального опору і відома вага літака, сам мінімальний опір можна знайти з
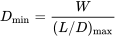
Прийнято вважати, що зв'язок між перетягуванням і підйомом - це те, що ми знайшли раніше, так званий параболічний опір полярний. Для параболічного опору полярного
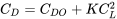
легко взяти похідну щодо коефіцієнта підйому і встановити її рівною нулю для визначення умов мінімального відношення коефіцієнта опору до коефіцієнта підйому, що було умовою мінімального опору.
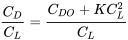
Отже,
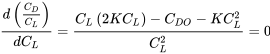
Це дає
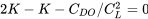
або
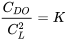
і
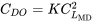
Вище наведена умова, необхідна для мінімального опору з параболічним опором полярним.
Тепер повертаємося до полярного перетягування
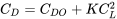
і для мінімального перетягування ми можемо написати
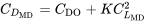
який, з вищесказаним, дає
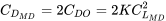
або
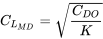
Виходячи з цього, ми можемо знайти значення максимального співвідношення ліфт-перетягування за базовими параметрами перетягування.
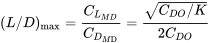
А швидкість, з якою це відбувається при прямому і рівному польоті, дорівнює
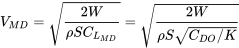
Таким чином, ми можемо записати мінімальну швидкість перетягування як
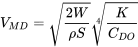
або еквівалентну мінімальну швидкість перетягування на рівні моря
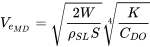
4.7 Огляд: Мінімальні умови перетягування для параболічного опору
На даний момент ми знаємо багато про мінімальні умови опору для літака з параболічним опором полярним у прямому та рівному польоті. Наступні рівняння можуть бути корисними для вирішення багатьох різних задач продуктивності, які будуть розглянуті пізніше в цьому тексті. Буде кілька умов польоту, які будуть оптимізовані при польоті в мінімальних умовах опору. Тому пропонується, щоб студент написав наступні рівняння на окремій сторінці в її або його класі замітки для зручності довідки.
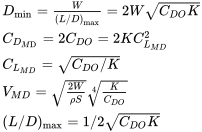
ПРИКЛАД 4.1
Літак, який важить 3000 фунтів, має площу крила 175 квадратних футів і співвідношення сторін сім з коефіцієнтом аеродинамічної ефективності крила (е) 0,95. Якщо базовий коефіцієнт опору, C DO, дорівнює 0,028, знайдіть мінімальний опір на рівні моря і на висоті 10 000 футів, максимальне відношення підйому до перетягування та значення коефіцієнта підйому та опору для мінімального опору. Також знайдіть швидкості для мінімального опору у прямому та рівному польоті як на рівні моря, так і на 10000 футів. Нам потрібно спочатку знайти термін K в рівнянні перетягування.
К = 1/(π ар) = 0,048
Тепер ми можемо знайти
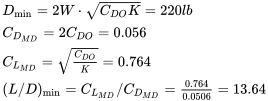
Ми можемо перевірити це за допомогою
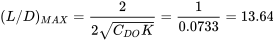
Швидкість мінімального опору є першою з них, яка залежить від висоти.
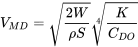
На рівні моря
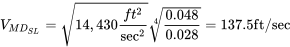
Щоб знайти швидкість для мінімального опору на 10000 футів, ми можемо перерахувати, використовуючи щільність на цій висоті, або ми можемо використовувати
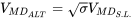
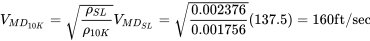
Передбачається, що в цей момент студент використовувати рівняння перетягування
і зробити графіки опору проти швидкості як для рівня моря, так і для умов висоти 10000 футів, будуючи значення опору з кроком 20 кадрів в секунду. Графіки підтверджуватимуть наведені вище значення мінімальної швидкості перетягування та мінімального опору.
4.8 Політ при мінімальному опорі
Одне питання, яке слід задати в цей момент, але, як правило, не відповідає в тексті на продуктивність літака є «Просто, як чорт візьми пілот робить цей літак літати в мінімальних умовах опору в будь-якому випадку?»
Відповідь, досить просто, полягає в тому, щоб літати на рівні моря еквівалентної швидкості для мінімальних умов опору. Пілот встановлює або «обрізає» літак літати на постійній висоті (прямо і рівно) на вказаній швидкості польоту (еквівалентна швидкість на рівні моря) для мінімального опору, як зазначено в посібнику з експлуатації літака. Все, що потрібно зробити пілоту, це тримати швидкість і висоту постійними.
4.9 Перетягніть стисливий потік
Для цілей вступного курсу з виконання літаків ми обмежилися обговоренням більш низької швидкості літаків; тобто літаки, що працюють в нестисливому потоці. Як обговорювалося раніше, аналітично, це обмежить нас розглядом швидкості польоту Маха 0,3 або менше (менше 300 кадрів в секунду на рівні моря), однак фізичні реалії початку опору зростання через ефекти стисливості дозволяють нам розширити наше використання нестисливої теорії до чисел Маха навколо 0,6 до 0,7. Це діапазон числа Маха, де надзвуковий потік над такими місцями, як верхня поверхня крила, досяг величини, що ударні хвилі можуть виникати під час уповільнення потоку, що призводить до втрат енергії через шок і опору піднімається через поділ потоку, викликаного ударом, над поверхнею крила. Цей підйом перетягування обговорювався в главі 3.
Оскільки швидкість піднімається до регіону, де слід враховувати ефекти стисненості, ми повинні враховувати швидкість звуку а та співвідношення питомих теплот повітря, гамма.
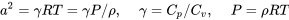
Гамма для повітря при нормальних більш низьких атмосферних температурах має значення 1,4.
Починаючи знову з відношення для параболічного опору полярного, ми можемо помножити і розділити на швидкість звуку, щоб переписати відношення через число Маха.
де
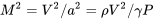
або
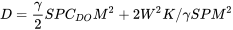
Отримане вище рівняння дуже схоже за формою на початкове полярне відношення перетягування і може бути використано подібним чином. Наприклад, щоб знайти число Маха для мінімального перетягування у прямому та рівному польоті, ми візьмемо похідну щодо числа Маха і встановимо результат рівним нулю. Ускладнення полягає в тому, що деякі терміни, які ми вважали постійними в нестисливих умовах, таких як K та CDO, тепер можуть бути функціями числа Маха і повинні бути так оцінені.
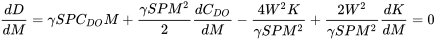
Часто рівняння вище потрібно вирішувати іттеративно.
4.10 Відгук
До цього моменту ми розглянули опір літака, заснованого насамперед на простій моделі, що використовує параболічне зображення опору в нестисливому потоці. Ми також обмежили наш аналіз прямим і рівним польотом, де підйом дорівнює вазі, а тяга дорівнює опору.
Літак може літати прямо і рівно з широким діапазоном швидкостей, за умови достатньої потужності або тяги, щоб зрівняти або подолати опір на цих швидкостях. Учень повинен розуміти фізичні аспекти цього польоту.
Ми дивилися на швидкість для прямого і рівного польоту при мінімальних умовах опору. Можна, звичайно, завжди круїз з такою швидкістю, і це може, насправді, бути дуже економічним способом літати (ми розглянемо це пізніше в обговоренні дальності та витривалості). Однак, оскільки «час - гроші», можуть бути підстави круїзувати на більш високих швидкостях. Це також може бути просто веселіше літати швидше. Політ з більшою, ніж мінімальною швидкістю перетягування, вимагатиме меншого кута атаки для отримання необхідного підйому (до рівної ваги), а верхня межа швидкості буде визначатися максимальною тягою або потужністю, доступною від двигуна.
Круїз з нижчою за мінімальну швидкість опору може бути бажаним при польоті підступах до посадки або при польоті в утриманні моделей або при польоті інших місій спеціального призначення. Для цього буде потрібно більший, ніж мінімальний кут атаки і використання більшої тяги або сили для подолання отриманого збільшення опору. Нижня межа швидкості може бути результатом опору, що досягає величини потужності або тяги, доступної від двигуна; однак, як правило, це буде результатом кута атаки, що досягає кута затримки. Отже, швидкість стійла зазвичай являє собою нижню межу прямої та рівної круїзної швидкості.
Потрібно пам'ятати, що все попереднє грунтується на припущенні прямого і рівного польоту. Якщо літак летить прямо і рівно з заданою швидкістю і додається потужність або тяга, літак спочатку як прискорюється, так і підніметься, поки не буде досягнуто нової рівноваги рівноваги рівноваги рівноваги на більшій висоті. Пілот може контролювати це додавання енергії, змінюючи ставлення літака (кут атаки), щоб направити додану енергію в бажану комбінацію збільшення швидкості та/або збільшення висоти. Якщо потужність двигуна зменшується, зазвичай можна очікувати зменшення висоти та/або швидкості, залежно від входу пілотного управління.
Тепер ми повинні додати коефіцієнт потужності двигуна, або тяги або потужності, до нашого розгляду продуктивності. Це нормально, щоб посилатися на вихід реактивного двигуна як тягу, а гвинтовий двигун як потужність. Ми спочатку розглянемо більш простий з двох випадків, тягу.
4.11 Тяга
Ми говорили, що для літака в прямому і рівному польоті тяга повинна дорівнювати опору. Якщо тяга двигуна літака перевищує опору для прямого та рівного польоту з заданою швидкістю, літак або підніметься, або прискорюється, або зробить обидва. Він також може бути використаний для здійснення поворотів або інших маневрів. Перетягування, що зустрічається у прямому та рівному польоті, тому можна назвати тягою, необхідною (для прямого та рівного польоту). Тяга, фактично вироблена двигуном, буде називатися наявною тягою.
Хоча ми можемо говорити про вихід будь-якого авіаційного двигуна з точки зору тяги, прийнято посилатися на тягу реактивних двигунів і потужність опорних двигунів. Пропелер, звичайно, виробляє тягу так само, як і потік від реактивного двигуна; однак, для двигуна, що живлять гвинт (або поршень або турбіна), вихід самого двигуна є потужність на вал. Таким чином, говорячи про таку рушійну установку, більшість посилань стосуються її потужності. Говорячи про сам гвинт, може використовуватися термінологія тяги.
Одиниці, що використовуються для обговорення тяги, - це Ньютони в системі СІ та фунти в англійській системі. Оскільки англійські одиниці фунтів все ще майже повсюдно використовуються, говорячи про тягу, вони зазвичай будуть використовуватися тут.
Тяга є функцією багатьох змінних, включаючи ефективність у різних частині двигуна, налаштування дросельної заслінки, висоту, число Маха та швидкість. Повне вивчення тяги двигуна буде залишено до більш пізнього курсу руху. Для наших цілей досить буде дуже простих моделей тяги з припущеннями, що тяга змінюється в залежності від щільності (висоти) і установки дросельної заслінки і, можливо, швидкості. Ми вже знайшли один такий зв'язок у другій главі з рівнянням імпульсу. Часто ми спростимо речі ще далі і припустимо, що тяга інваріантна зі швидкістю для простого реактивного двигуна.
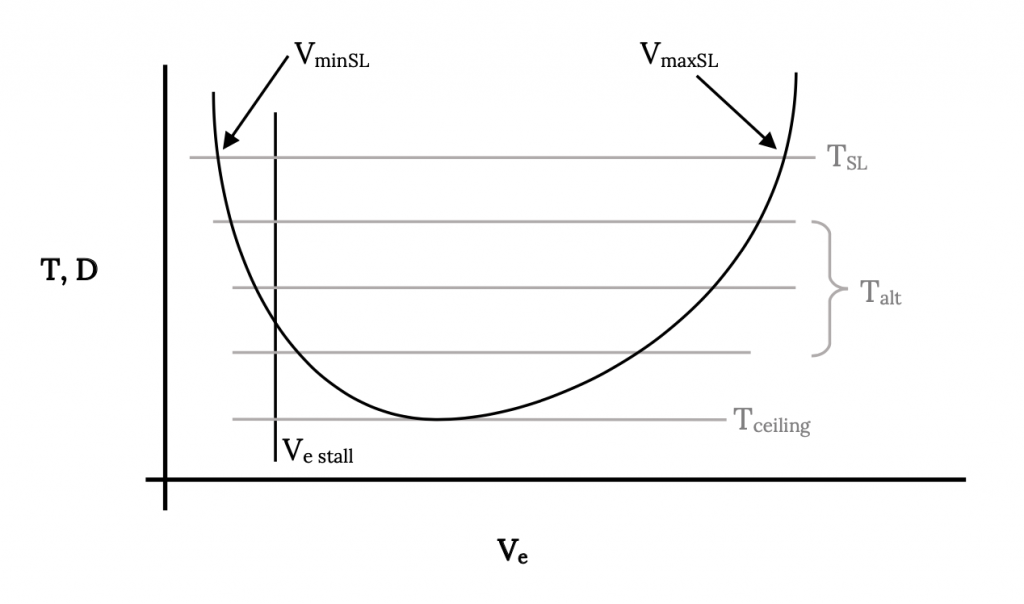
Якщо ми знаємо варіацію тяги зі швидкістю та висотою для даного літака, ми можемо додати криві тяги двигуна до кривих опору для прямого та рівного польоту для цього літака, як показано нижче. Зазвичай ми припускаємо, що оскільки нас цікавлять межі продуктивності для літака, нас цікавить лише випадок 100% налаштування дросельної заслінки. Очевидно, що інші настройки дросельної заслінки дадуть тяги в будь-якій точці нижче 100% кривих для тяги.
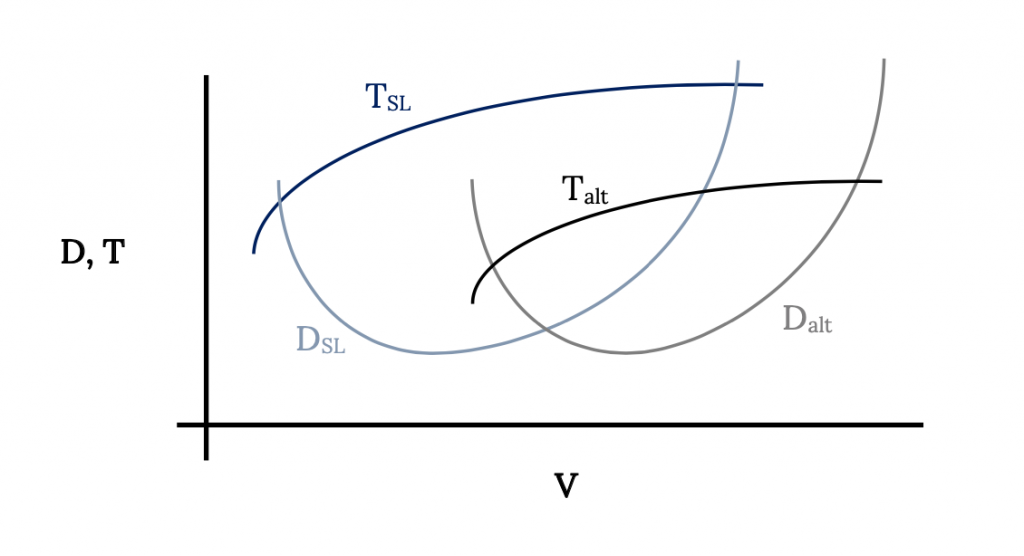
На малюнку вище слід зазначити, що, хоча термінологія використовується тяга і тяга, може бути більш значущим називати ці криві тяги наявної і тяги, необхідної при зверненні до потужності двигуна і опору літака відповідно.
4.12 Мінімальна і максимальна швидкість
Перетину кривих тяги і тяги на малюнку вище очевидно представляють мінімальну і максимальну швидкість польоту при прямому і рівному польоті. Вище максимальної швидкості є недостатня тяга, доступна від двигуна для подолання опору (потрібна тяга) літака на цих швидкостях. Те ж саме справедливо і нижче перетину нижньої швидкості двох кривих.
Справжнє нижнє обмеження швидкості для літака зазвичай накладається стійлом, а не перетином кривих тяги та перетягування. Швидкість зупинки може бути додана до графіку, як показано нижче:
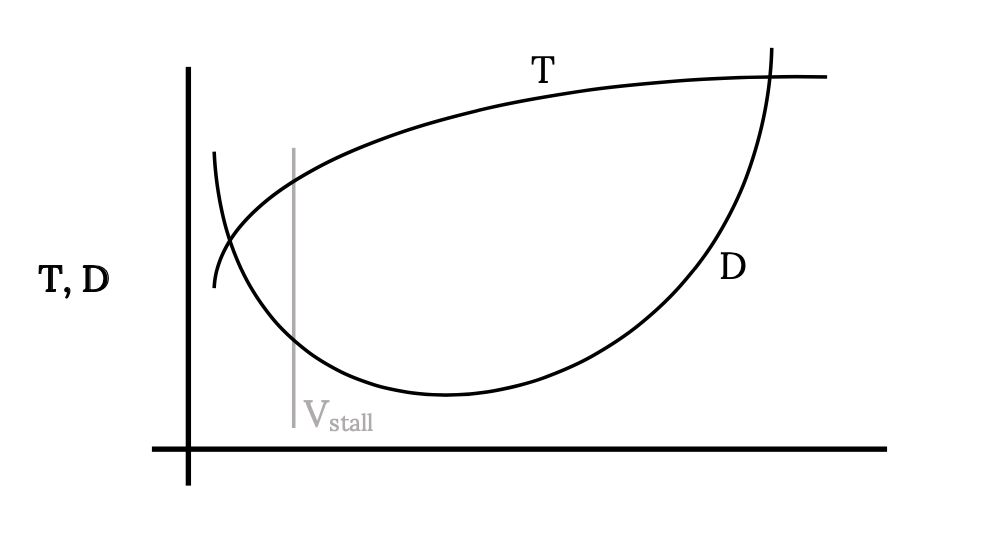
Область між наявною тягою та необхідними кривими перетягування або тяги можна назвати конвертом польоту. Літак може літати прямо і рівно з будь-якою швидкістю між цими верхніми і нижніми точками перетину швидкості. Між цими обмеженнями швидкості є надлишкова тяга, яка може бути використана для польоту, крім прямого та рівного польоту. Цю зайву тягу можна використовувати для підйому або повороту або маневру іншими способами. Деякі з цих маневрів ми розглянемо в наступному розділі. Поки ми обмежимо наше розслідування сферою прямого та рівного польоту.
Зверніть увагу, що на більшій висоті зменшення наявної тяги зменшило «конверт польоту», наблизивши верхні та нижні обмеження швидкості та зменшивши надлишкову тягу між кривими. Оскільки тяга постійно зменшується зі збільшенням висоти, конверт польоту продовжуватиме скорочуватися, поки верхня та нижня швидкості не стануть рівними, а дві криві просто торкнуться. Це можна побачити більш чітко на малюнку нижче, де всі дані побудовані з точки зору еквівалентної швидкості рівня моря. У наведеному прикладі тяга, наявна на h 6, повністю падає нижче необхідної кривої опору або тяги. Це означає, що літак не може літати прямо і рівно на цій висоті. Ця висота, як кажуть, вище «стелі» для літака. На деякій висоті між h 5 і h 6 футів буде доступна крива тяги, яка буде просто торкнутися кривої перетягування. Ця висота буде висотою стелі літака, висотою, на якій літак може літати лише з однією швидкістю. Ми будемо мати більше сказати про визначення стелі в наступному розділі.
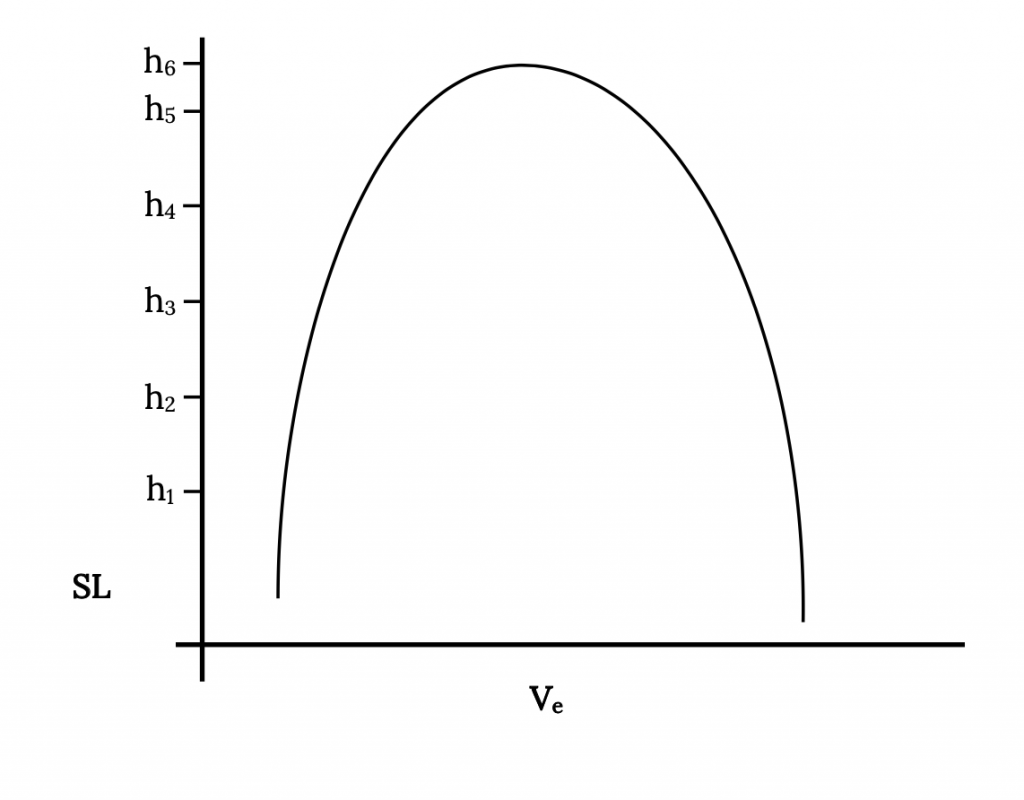
Інший спосіб подивитися на ці ж межі швидкості та висоти - це побудувати перехрестя тяги та перетягнути криві на наведеній вище фігурі проти висоти, як показано нижче. Це показує іншу версію оболонки польоту з точки зору висоти та швидкості. Цей тип сюжету більш значущий для пілота та інженера льотних випробувань, оскільки швидкість і висота - це два параметри, показані на стандартних приладах літальних апаратів, а тяги немає.
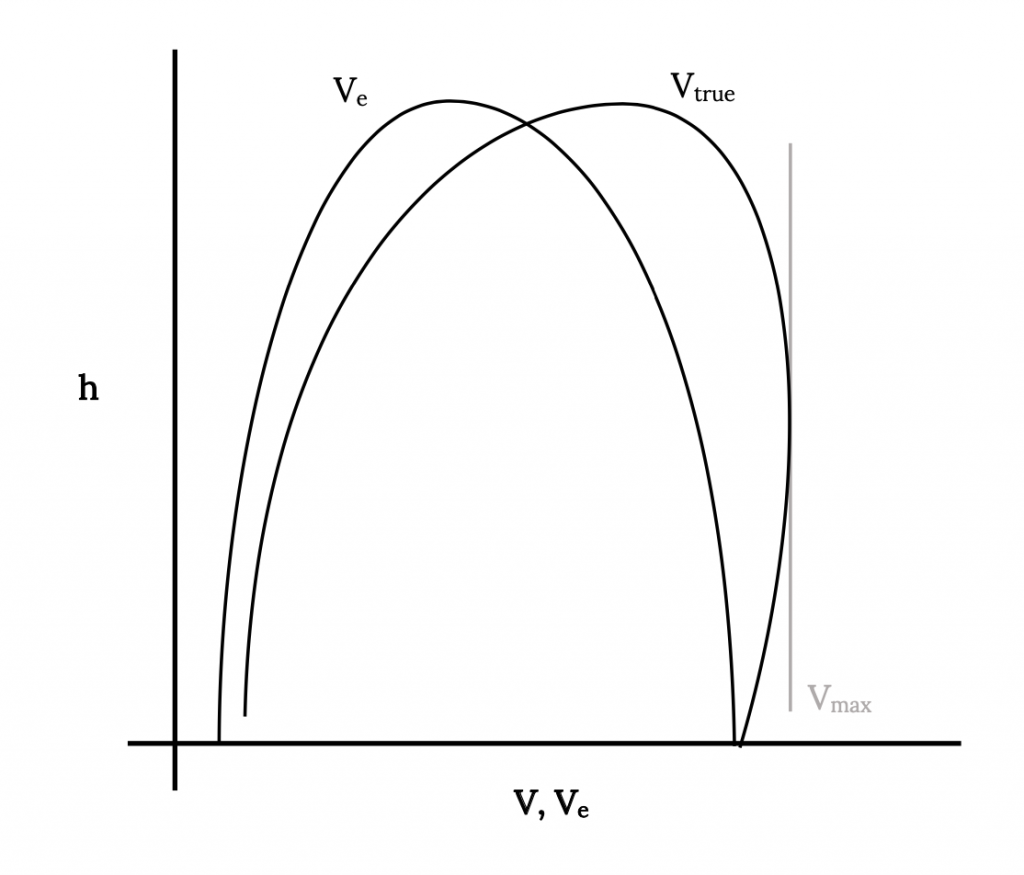
Також може бути доцільним додати до малюнка вище графік тих же даних, використовуючи фактичну швидкість польоту, а не вказану або еквівалентну швидкості повітря на рівні моря. Це можна зробити досить просто, використовуючи квадратний корінь співвідношення щільності (рівень моря до висоти), як обговорювалося раніше, щоб перетворити еквівалентні швидкості на фактичні швидкості. Це показано на графіку нижче. Зверніть увагу, що на рівні моря V = Ve а також буде деяка висота, де є максимальна істинна швидкість польоту.
4.13 Особливий випадок постійної тяги
Дуже проста модель часто використовується для тяги від реактивного двигуна. Зроблено припущення, що тяга постійна на заданій висоті. Ми будемо використовувати це припущення як нашу стандартну модель для всіх реактивних літаків, якщо інше не зазначено в прикладах або проблемах. Пізніше ми обговоримо моделі для варіації тяги з висотою.
Наведена вище модель (постійна тяга на висоті), очевидно, дає можливість знайти досить просте аналітичне рішення для перетинів наявної тяги і кривих опору (потрібна тяга). Допустимо тягу рівною константі
Т = Т 0
Тому в прямому і рівному польоті, де тяга дорівнює перетягуванню, ми можемо написати
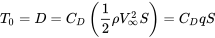
де q - це загальноприйнята абревіатура для динамічного тиску.
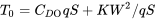
або
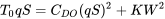
і перестановка як квадратне рівняння
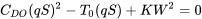
Розв'язування наведеного вище рівняння дає
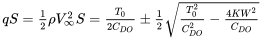
або
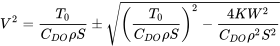
У перерахунку на рівень моря еквівалентна швидкості
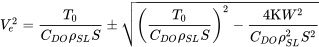
Ці рішення, звичайно, дворазово оцінюються. Більш висока швидкість - це максимальна пряма і рівна швидкість польоту на розглянутій висоті, а нижчим рішенням є номінальна мінімальна пряма і рівна швидкість польоту (швидкість стійла, ймовірно, буде більшою швидкістю, що представляє справжню мінімальну швидкість польоту).
Існують, звичайно, і інші способи вирішення для перетину кривих тяги і перетягування. Іноді зручно вирішувати рівняння коефіцієнтів підйому на мінімальній і максимальній швидкостях. Щоб налаштувати таке рішення, спочатку повернемося до базових рівнянь прямого і рівневого польоту T = T 0 = D і L = W.
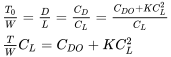
або
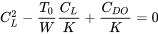
рішення для CL
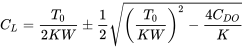
Таке рішення дасть два значення коефіцієнта підйому. Більша з двох значень представляє мінімальну швидкість польоту для прямого та рівного польоту, тоді як менша C L - для максимальної швидкості польоту. Швидкість відповідності знаходить з співвідношення
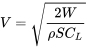
4.14 Огляд для Постійна тяга
На малюнку нижче графічно показаний розглянутий вище випадок. З розв'язку тяги дорівнює опору ми отримуємо два значення або коефіцієнта підйому, або швидкості, одне для максимальної прямої та рівної швидкості польоту на обраній висоті, а інше для мінімальної швидкості польоту. Швидкість стійла, ймовірно, перевищить мінімальну пряму і рівень швидкості польоту знайдені з тяги дорівнює перетягнути рішення, що робить його справжньою мінімальною швидкістю польоту.
Зі збільшенням висоти T 0 зазвичай зменшується, а V MIN і V MAX рухатимуться разом, поки на висоті стелі вони не зливаються, щоб стати єдиною точкою.
Зазвичай передбачається, що тяга реактивного двигуна буде змінюватися в залежності від висоти прямо пропорційно зміні щільності. Це припущення підтверджується рівняннями тяги для реактивного двигуна, оскільки вони походять від рівнянь імпульсу, представлених у другій главі цього тексту. Тому ми можемо написати:
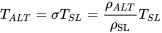
ПРИКЛАД 4.2
Раніше в цьому розділі ми розглянули літак 3000 фунтів з площею крила 175 квадратних футів, співвідношення сторін сім і C DO 0,028 з е = 0,95. Скажімо, літак оснащений невеликим реактивним двигуном, який має постійну тягу на рівні моря 400 фунтів. Знайдіть максимальну та мінімальну пряму та рівну швидкість польоту для цього літака на рівні моря та на відстані 10000 футів, припускаючи, що наявна тяга змінюється пропорційно щільності.
Якщо, як було запропоновано раніше, студент, побудував криві перетягування для цього літака, графічне рішення просте. Потрібно лише додати пряму лінію, що представляє 400 фунтів до ділянки рівня моря, і перетину цієї лінії з кривою перетягування рівня моря дають відповідь. Те ж саме можна зробити з даними висоти 10 000 футів, використовуючи постійну тягу, зменшену пропорційно щільності.
Враховуючи стандартну щільність атмосфери 0,001756 сл/фут 3, тяга на 10000 футів буде в 0,739 рази більше тяги рівня моря або 296 фунтів. Використовуючи два наявні значення тяги, ми можемо вирішити для обмежень швидкості на рівні моря і на l0,000 футів.
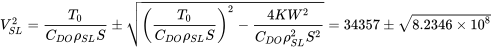
= 63053 або 5661
V SL = 251 фут/сек (макс)
або = 75 футів/сек (хв)
Таким чином, рівняння дає максимальну і мінімальну пряму і рівну швидкість польоту як 251 і 75 футів в секунду відповідно.
Передбачається, що студент робити подібні розрахунки для випадку висоти 10000 футів. Зауважте, що не можна просто взяти рішення швидкості рівня моря вище і перетворити їх на швидкості на висоті, використовуючи квадратний корінь коефіцієнта густини. Рівняння повинні бути вирішені знову, використовуючи нову тягу на висоті. Студент також повинен порівняти результати аналітичного рішення з графічними результатами.
Як уже згадувалося раніше, швидкість стійла зазвичай є фактичною мінімальною швидкістю польоту. Якщо максимальний коефіцієнт підйому має значення 1,2, знайдіть швидкості стійла на рівні моря і додайте їх до своїх графіків.
4.15 Продуктивність з точки зору потужності
Потужність двигуна всіх повітряних суден, що працюють на гвинтах, виражається в плані потужності. Потужність - це дійсно енергія в одиницю часу. Хоча сам вихід гвинта може бути виражений як тяга при бажанні, звичайно також висловлювати його з точки зору потужності.
Хоча на перший погляд може здатися, що потужність і тяга дуже різні параметри, вони пов'язані дуже просто через швидкість. Потужність тяги множиться на швидкість. Одиницями для потужності є ньютон-метри в секунду або ват в системі СІ і кінські сили в англійській системі. Як і раніше, ми будемо використовувати в першу чергу англійську систему. Причина досить очевидна. Автор кидає виклик будь-кому, щоб знайти будь-якого пілота, механіка або навіть будь-якого водія автомобіля в будь-якій точці світу, який може заявити рейтинг потужності для свого двигуна у ватах! Ватти призначені для лампочок: кінські сили - для двигунів!
Власне, наші рівняння призведуть до англійської системи силових одиниць фут-фунтів в секунду. Конверсія є
один HP = 550 фут-фунтів/секунду.
Ми будемо говорити про два типи потужності; потужність, доступну та необхідну потужність. Необхідна потужність - це потужність, необхідна для подолання опору літака
П реак = Д х В
Доступна потужність дорівнює тязі, помноженої на швидкість.
Р ав = Т х В
Слід зазначити, що ми можемо почати з потужності і знайти тягу, діливши на швидкість, або ми можемо помножити тягу на швидкість, щоб знайти потужність. Немає підстав не говорити про тягу пропелерної рушійної установки або про потужність реактивного двигуна. Використання потужності для пропелерних систем і тяги для струменів просто дотримується конвенції, а також визнає, що для струменя тяга відносно постійна зі швидкістю, а для опори потужність відносно інваріантна зі швидкістю.
Потужність доступна - це потужність, яку можна отримати від гвинта. Визнаючи, що між двигуном та гвинтом є втрати, ми розрізнимо наявну потужність та кінську силу вала. Вал кінської сили - це потужність, що передається через кривошип або приводний вал до гребного гвинта від двигуна. Двигун може бути поршневим або турбінним або навіть електричним або паровим. Гребний гвинт перетворює цю потужність вала (Ps) в пропульсивну потужність з певним пропульсивним ККД, η p.
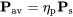
Ефективність руху - це функція швидкості гвинта, швидкості польоту, конструкції гвинта та інших факторів.
Очевидно, що як доступна потужність, так і необхідна потужність є функціями швидкості, як через термін швидкості у співвідношенні, так і від зміни як опору, так і тяги зі швидкістю. Для ідеального реактивного двигуна, який ми припускаємо, що мають постійну тягу, зміна потужності доступна просто лінійне збільшення зі швидкістю.
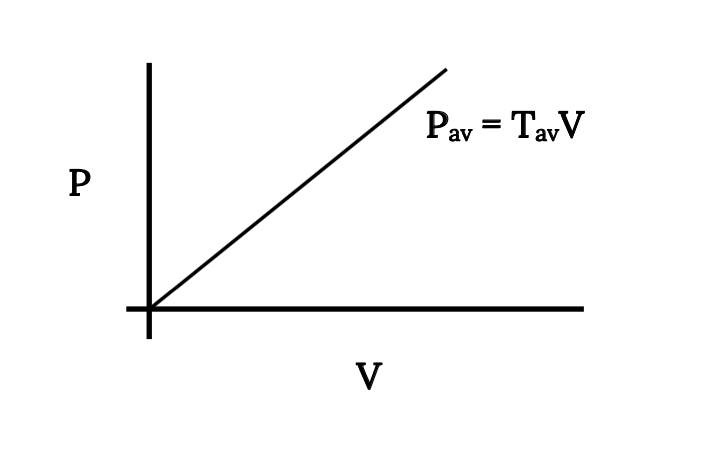
Цікаво, що якщо ми працюємо з струменем, де тяга постійна по відношенню до швидкості, рівняння вище дають нульову потужність при нульовій швидкості. Це не інтуїтивно зрозуміло, але, тим не менш, вірно і матиме цікаві наслідки, коли ми пізніше вивчимо темпи підйому.
Іншим наслідком цього співвідношення між тягою та потужністю є те, що якщо потужність приймається постійною щодо швидкості (як ми будемо робити для опорних літаків) тяга стає нескінченною, оскільки швидкість наближається до нуля. Це означає, що Cessna 152, коли стоїть на місці з двигуном працює, має нескінченно більше тяги, ніж Boeing 747 з двигунами, що працюють повний вибух. Він також має більшу потужність! Яке його поштовх для приватного пілота!
Використовуючи концепцію потужності для вивчення продуктивності літака, ми зробимо те ж саме, що ми робили за допомогою тяги. Ми будемо говорити про перетин необхідної потужності і потужності доступних кривих, що визначають максимальну і мінімальну швидкості. Ми знайдемо швидкість для мінімальної необхідної потужності. Ми розглянемо варіацію цих з висотою. Графіки, які ми будуємо, будуть виглядати так нижче.
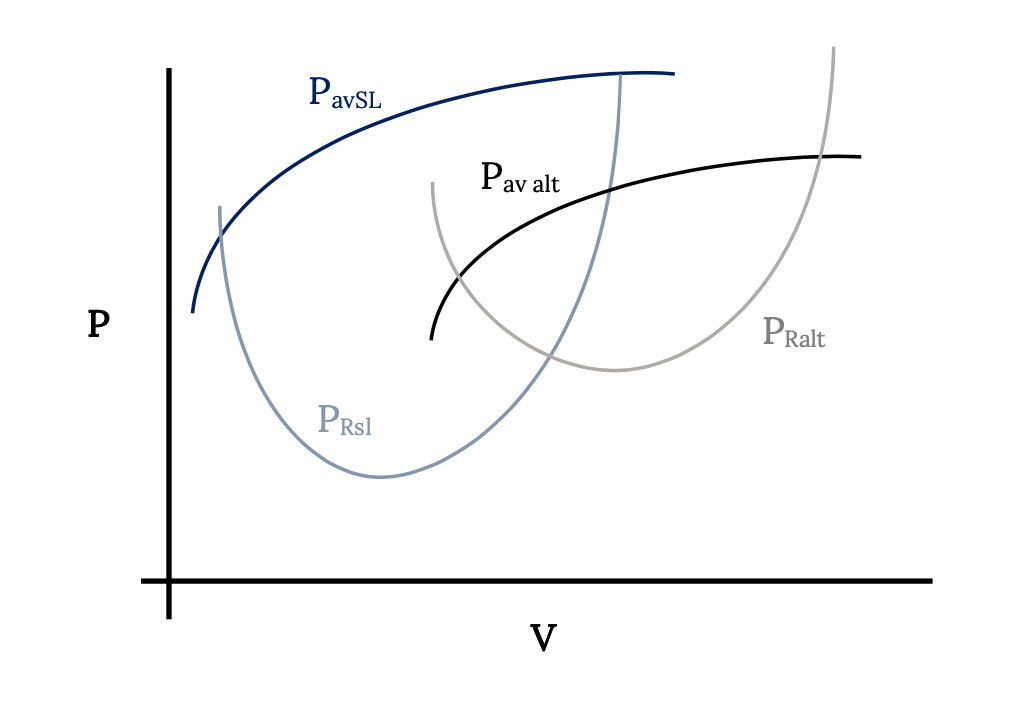
Хоча максимальна і мінімальна пряма і рівна швидкість польоту, яку ми визначаємо за кривими потужності, будуть ідентичні тим, що знайдені з даних тяги, будуть деякі відмінності. Одну відмінність можна відзначити з наведеного вище малюнка. На відміну від мінімального опору, який був однаковою величиною на кожній висоті, мінімальна потужність буде різною на кожній висоті. Це означає, що буде складніше згорнути дані на всіх висотах в єдину криву.
4.16 Необхідна потужність
Потужність необхідної ділянки буде виглядати дуже схожою на ту, яку бачили раніше для необхідної тяги (перетягнути). Це просто перетягування, помножене на швидкість. Якщо ми продовжуємо припускати параболічний опір полярний з постійними значеннями CDO та K, ми маємо наступне співвідношення для необхідної потужності:
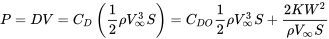
Ми можемо побудувати це для заданих значень C DO, K, W і S (для даного літака) для різних висот, як показано в наступному прикладі.
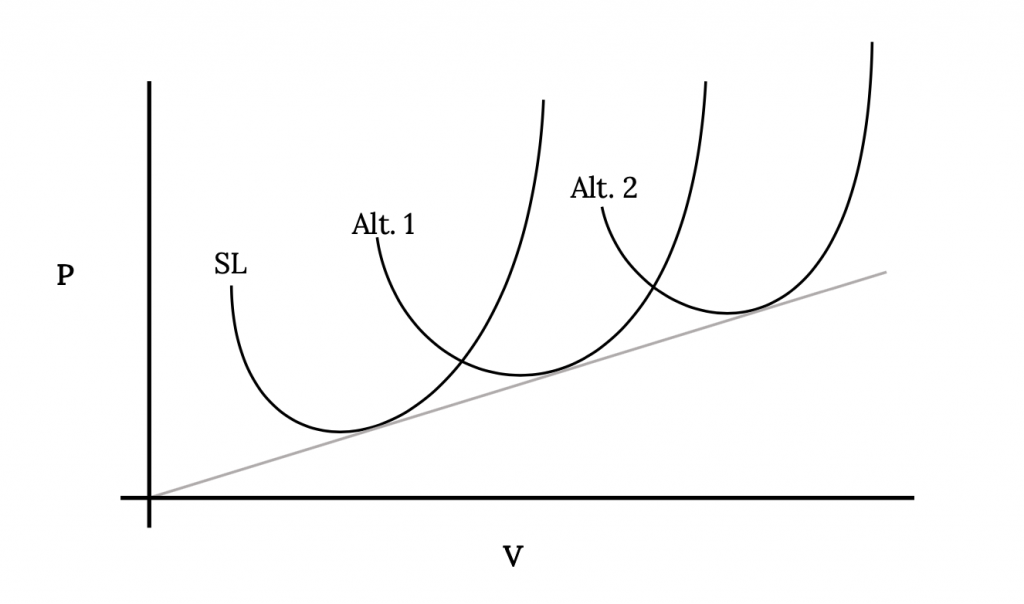
Відзначимо, що мінімальні значення потужності не будуть однаковими на кожній висоті. Нагадуючи, що мінімальні значення опору були однаковими на всіх висотах і що необхідна потужність - це швидкість перетягування разів, логічно, що мінімальне значення потужності зростає лінійно зі швидкістю. Ми повинні мати можливість провести пряму лінію від початку через мінімальну потужність необхідних точок на кожній висоті.
Мінімальна потужність, необхідна при прямому та рівному польоті, звичайно, може бути взята з ділянок, подібних до наведеного вище. Ми також хотіли б визначити значення коефіцієнта підйому та опору, які призводять до мінімальної потужності, необхідної так само, як ми це робили для мінімального опору.
Спочатку можна припустити, що мінімальна потужність для даного літака відбувається в тих же умовах, що і для мінімального опору. Це, звичайно, невірно через додану залежність потужності від швидкості. Ми можемо почати розуміти параметри, які впливають на мінімально необхідну потужність, знову повернувшись до наших простих рівнянь балансу сили для прямого і рівного польоту:
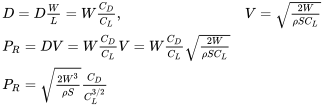
Таким чином, для даного літака (вага і площа крила) і висоти (щільність) мінімально необхідна потужність для прямого і рівного польоту виникає, коли коефіцієнт опору, поділений на коефіцієнт підйому до потужності в дві третини, є мінімальним.
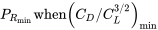
Припускаючи параболічний опір полярний, ми можемо написати рівняння для наведеного вище співвідношення коефіцієнтів і взяти його похідну по відношенню до коефіцієнта підйому (так як C L лінійний з кутом атаки, це те ж саме, що шукати максимум в діапазоні кута атаки) і встановити його рівним нулю знайти максимум.
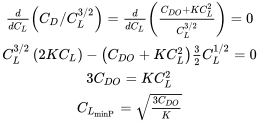
Зауважте, що
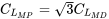
Коефіцієнт підйому для мінімальної необхідної потужності вище (1,732 рази), ніж для мінімальних умов опору.
Знаючи коефіцієнт підйому для мінімально необхідної потужності легко знайти швидкість, з якою це буде відбуватися.
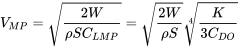
Зверніть увагу, що швидкість для мінімальної необхідної потужності нижча, ніж для мінімального опору.
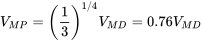
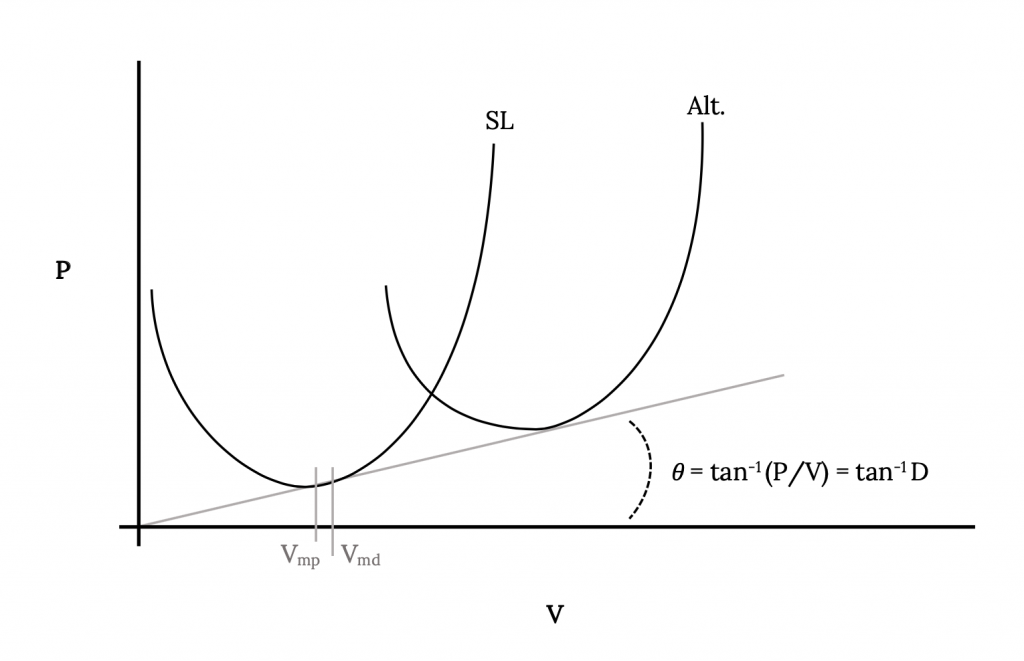
Мінімальна необхідна потужність та мінімальні швидкості опору можна знайти графічно з необхідної потужності ділянки. Мінімальна потужність, очевидно, знаходиться в нижній частині кривої. Розуміючи, що перетягування - це сила, розділена на швидкість і що лінія, проведена від початку до будь-якої точки кривої потужності, знаходиться під кутом до осі швидкості, дотичною якої є сила, розділена на швидкість, тоді лінія, яка стосується кривої з найменшим кутом, повинна торкнутися її при мінімальному стані опору. З цього ми можемо графічно визначити потужність і швидкість при мінімальному опорі, а потім розділити перший на останній, щоб отримати мінімальний опір. Зауважте, що цей графічний метод працює навіть для випадків непараболічного перетягування. Оскільки ми знаємо, що всі висоти дають однаковий мінімальний опір, всі криві потужності, необхідні для різних висот, будуть дотичними до цієї ж лінії, а точка дотику є мінімальною точкою опору.
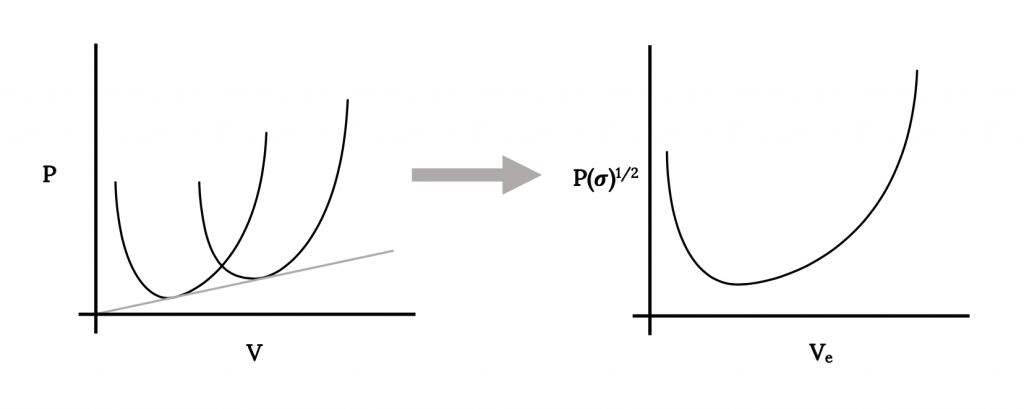
Ще один пункт, який слід враховувати при розгляді графічного зображення необхідної потужності, - це умова, необхідна для згортання даних для всіх висот до однієї кривої. У разі необхідної тяги або перетягування це було досягнуто шляхом простого побудови опору з точки зору еквівалентної швидкості на рівні моря. Це не спрацює в цьому випадку, оскільки крива потужності, необхідної для кожної висоти, має різний мінімум. Побудова всіх даних з точки зору Ve стискає криві щодо швидкості, але не щодо потужності. Результатом буде такий сюжет:
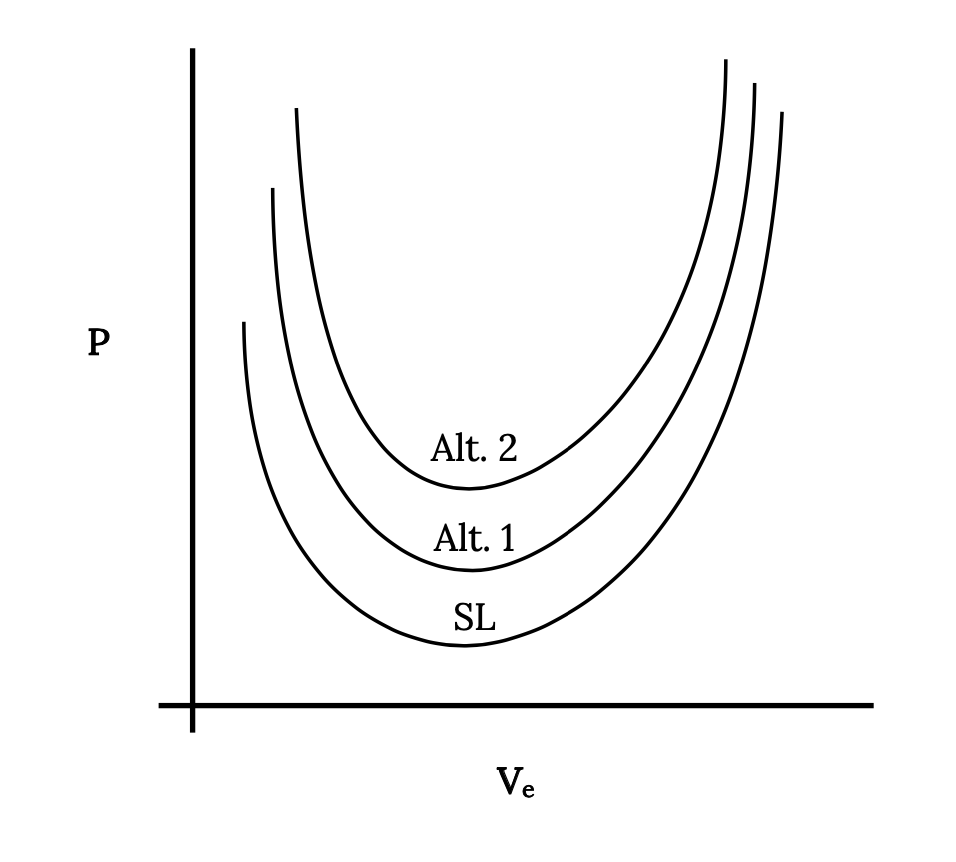
Знаючи, що необхідна потужність - це швидкість перетягування, ми можемо пов'язати потужність, необхідну на рівні моря, з потужністю на будь-якій висоті.
або
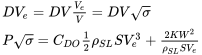
Результатом є те, що для того, щоб згорнути всі необхідні потужності дані до однієї кривої, ми повинні побудувати потужність, помножену на квадратний корінь сигми проти еквівалентної швидкості рівня моря. Таким чином, це буде нашою конвенцією у побудові даних про потужність.
4.17 Відгуків
У попередньому ми знайшли наступні рівняння для визначення мінімальної потужності необхідних умов:
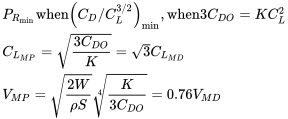
Ми також можемо написати
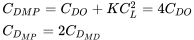
Таким чином, коефіцієнт опору для мінімальної потужності необхідних умов в два рази більше, ніж для мінімального опору. Ми також можемо написати
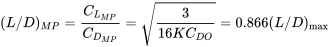
Оскільки мінімальна потужність необхідні умови є важливими і будуть використані пізніше для пошуку інших параметрів продуктивності, пропонується, щоб студент написав вищезазначені відносини на спеціальній сторінці в своїх примітках для зручності довідки.
Пізніше ми розглянемо повний погляд на справу з наявною потужністю. Якщо ми знаємо доступну потужність, ми можемо, звичайно, написати рівняння з необхідною потужністю, прирівненою до наявної потужності, і вирішити максимальну та мінімальну пряму та рівну швидкість польоту так само, як ми це робили з рівняннями тяги. Рівняння потужності, однак, не такі прості, як рівняння тяги через їх залежність від куба швидкості. Часто найкращим рішенням є іттеративне.
Якщо потужність, наявна від двигуна, є постійною (як це зазвичай передбачається для опорного двигуна), співвідношення, що прирівнює наявну потужність та необхідну потужність, є
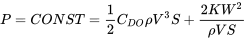
Для реактивного двигуна, де тяга моделюється як константа, рівняння зводиться до того, що використовувалося в попередньому розділі на розрахунках продуктивності на основі тяги.
ПРИКЛАД 4.3
Для того ж літака 3000 фунтів, який використовувався в попередніх прикладах, обчислити швидкість для мінімальної потужності.
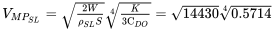
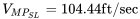
- Пропонується, щоб студент склав ділянки потужності, необхідної для прямого і рівного польоту на рівні моря і на висоті 10000 футів і графічно перевірити вищевказані розрахункові значення.
- Також пропонується, щоб з цих сюжетів студент знаходив швидкості для мінімального перетягування і порівняв їх з тими, що були знайдені раніше.
4.18 Резюме
У цій главі розглянуто кілька елементів виконання в прямому і рівному польоті. Запропоновано просту модель зміни опору зі швидкістю (параболічний опір полярний), яка була використана для розробки рівнянь для розрахунків умов мінімального опору польоту та пошуку максимальної та мінімальної швидкостей польоту на різних висотах. Також було наголошено на графічних методах, і слід ще раз зазначити, що ці графічні методи працюватимуть незалежно від використовуваної моделі перетягування.
Настійно рекомендується, щоб студент потрапив у звичку ескізувати графік тяги та/або кривих потужності проти швидкості як допоміжний засіб візуалізації для кожної проблеми, навіть якщо рішення, яке використовується, є повністю аналітичним. Такі ескізи можуть стати цінним інструментом у розвитку фізичного відчуття проблеми та її вирішення.
Домашнє завдання 4
1. Використовуйте теорему імпульсу, щоб знайти тягу для реактивного двигуна, де відомі наступні умови:
| швидкість на вході | 300 кадрів в секунду |
| щільність вхідного потоку | 0,0023 сл/фут ^ 3 |
| площа вхідного отвору | 4 футів ^ 2 |
| швидкість вихідного потоку | 1800 кадрів в секунду |
| щільність вихідного потоку | невідомий |
| зона виходу | 2 футів ^ 2 |
| витрата палива | 5 фунтів_м/сек |
Припустимо стійкий потік і що тиск на вході і виході є атмосферними.
2. Ми виявили, що тяга від гвинта може бути описана рівнянням T = T 0 — aV 2. Виходячи з цього рівняння, опишіть, як би ви створили простий експеримент аеродинамічної труби для визначення значень для T 0 і a для моделі двигуна літака. Припустімо, що у вас є доступ до аеродинамічної труби, піто-статичної трубки, манометра U-трубки та тензодатчика, який буде вимірювати тягу. Намалюйте ескіз вашого експерименту.
Посилання
Малюнок 4.1: Родинний сірий (2021). «Статичний баланс сили в прямому і рівному польоті». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.1_20210804
Малюнок 4.2: Родинний сірий (2021). «Різні типи стійла». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.2_20210804
Малюнок 4.3: Родинний сірий (2021). «Частина перетягування збільшується з квадратом швидкості.» CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.3_20210804
Малюнок 4.4: Родинний сірий (2021). «Частина перетягування зменшується зі швидкістю в квадраті.» CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.4_20210804
Малюнок 4.5: Родинний сірий (2021). «Загальна зміна перетягування зі швидкістю». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.5_20210804
Малюнок 4.6: Родинний сірий (2021). «Вплив висоти на зміну перетягування». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Отримано з https://archive.org/details/4.6_20210804
Малюнок 4.7: Родинний сірий (2021). «Еквівалентна (вказана) швидкість перетягування проти рівня моря». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.7_20210804
Малюнок 4.8: Родинний сірий (2021). «Графічний метод визначення мінімальних умов перетягування». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.8_20210805
Малюнок 4.9: Родинний сірий (2021). «Варіація тяги та перетягування зі швидкістю». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/4.9_20210805
Малюнок 4.10: Родинний сірий (2021). «Мінімальна і максимальна швидкість для прямого та рівного польоту». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.10_20210805
Малюнок 4.11: Родинний сірий (2021). «Варіація тяги з висотою проти еквівалентної швидкості рівня моря». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.11_20210805
Малюнок 4.12: Родинний сірий (2021). «Прямий та рівний конверт швидкості польоту з висотою». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.12_20210805
Малюнок 4.13: Родинний сірий (2021). «Справжня максимальна швидкість польоту проти висоти». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.13_20210805
Малюнок 4.14: Родинний сірий (2021). «Графічне рішення для постійної тяги на кожній висоті». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.14_20210805
Малюнок 4.15: Родинний сірий (2021). «Доступна потужність змінюється лінійно зі швидкістю». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.15_20210805
Малюнок 4.16: Родинний сірий (2021). «Необхідна потужність та доступна варіація з висотою». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.16_20210805
Малюнок 4.17: Родинний сірий (2021). «Потужність необхідна варіація з висотою». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.17_20210805
Малюнок 4.18: Родинний сірий (2021). «Графічне визначення мінімального опору та мінімальних швидкостей потужності». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.18_20210805
Малюнок 4.19: Родинний сірий (2021). «Ділянка необхідної потужності проти еквівалентної швидкості на рівні моря». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.19_20210805
Малюнок 4.20: Родинний сірий (2021). «Стиснення енергетичних даних до єдиної кривої». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/4.20_20210805
<! — pb_fixme —><! — pb_fixme —>
