1: Вступ до аеродинаміки

Last updated

Oct 25, 2022
Save as PDF
- Вступ
- 2: Двигун

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Глава 1. Вступ до аеродинаміки

1.1 Аеродинаміка

Аеродинаміка - це, мабуть, перший предмет, який спадає на думку, коли більшість людей думають про авіаційну або аерокосмічну техніку. Аеродинаміка - це, по суті, застосування класичних теорій «механіки рідини» до зовнішніх потоків або потоків навколо тіл, і основне застосування, яке спадає на думку більшості аероінженерів, - це обтікання крил.

Крило є найважливішою частиною літака, тому що без нього не було б ніякого ліфта і не літак. Більшість людей мають деяке уявлення про те, як працює крило; тобто, змушуючи потік над верхньою частиною крила йти швидше, ніж потік над дном, ми отримуємо менший тиск на верхній, ніж на нижній, і, як наслідок, отримуємо підйом. Аероінженер повинен знати щось більше, ніж це. Аероінженер повинен знати, як сформувати крило, щоб отримати оптимальну комбінацію моменту підйому та перетягування та пітчингу для певної місії літака. Крім того, йому потрібно зрозуміти, як аеродинаміка транспортного засобу взаємодіє з іншими аспектами його дизайну та продуктивності. Також було б непогано, якби сили на крило не перевищували межу навантаження конструкції крила.

Якщо хтось дивиться на достатню кількість літаків, минуле і сьогодення, він або вона знайде широкий спектр форм крил. Деякі літаки мають короткі, в'юнкі крила (малий розмах крил), а інші мають довгі вузькі крила. Деякі крила змітаються, а інші прямі. Крила можуть мати непарні форми на кінчиках або навіть кріплення та розширення, такі як крила. Всі ці форми пов'язані з призначенням і конструкцією літака.

Для того, щоб подивитися, чому крила мають форму, ми повинні почати з розгляду термінів, які використовуються для визначення форми крила.

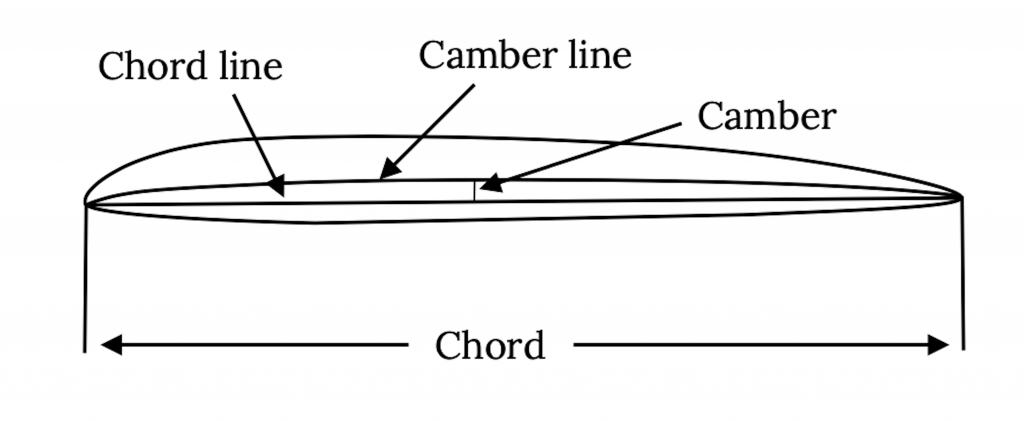
Аерофольг показано прямою лінією, що з'єднує провідний і кінцевий краї, позначені лінією хорди. Довжина аеролиста позначається як хорда. Лінія розвалу - це середня площина між верхньою та нижньою поверхнями аеропрофілю, при цьому відстань між лінією розвалу та горизонтальною лінією хорди позначається як розвал. — Малюнок 1.1: Термінологія аерокрила

Двомірний зріз крила, вирізаного паралельно центральній лінії фюзеляжу літака або кузова, називається секцією аеропрофілю. Пряма лінія від переднього краю перерізу аеропрофілю до його заднього краю називається лінією хорди. Довжина лінії акорду іменується як акорд. Лінія, проведена на півдорозі між верхньою та нижньою поверхнями секції аеропрофілю, називається лінією розвалу. Максимальна відстань між лінією розвалу та лінією хорди називається розгином аеропрофілю і зазвичай перераховується як відсоток хорди. Ми побачимо, що кількість розвалу аеропрофілю та розташування точки максимального розвалу є важливими цифрами у визначенні форми аеропрофілю та прогнозуванні його продуктивності. Для більшості аеродинамічних профілів максимальний розвал знаходиться на порядку від нуля до п'яти відсотків, а розташування точки максимального розвалу становить від 25% до 50% хорди від передньої кромки аеропрофілю.

При погляді зверху літака форма крила або плоскаформа визначається іншими термінами.

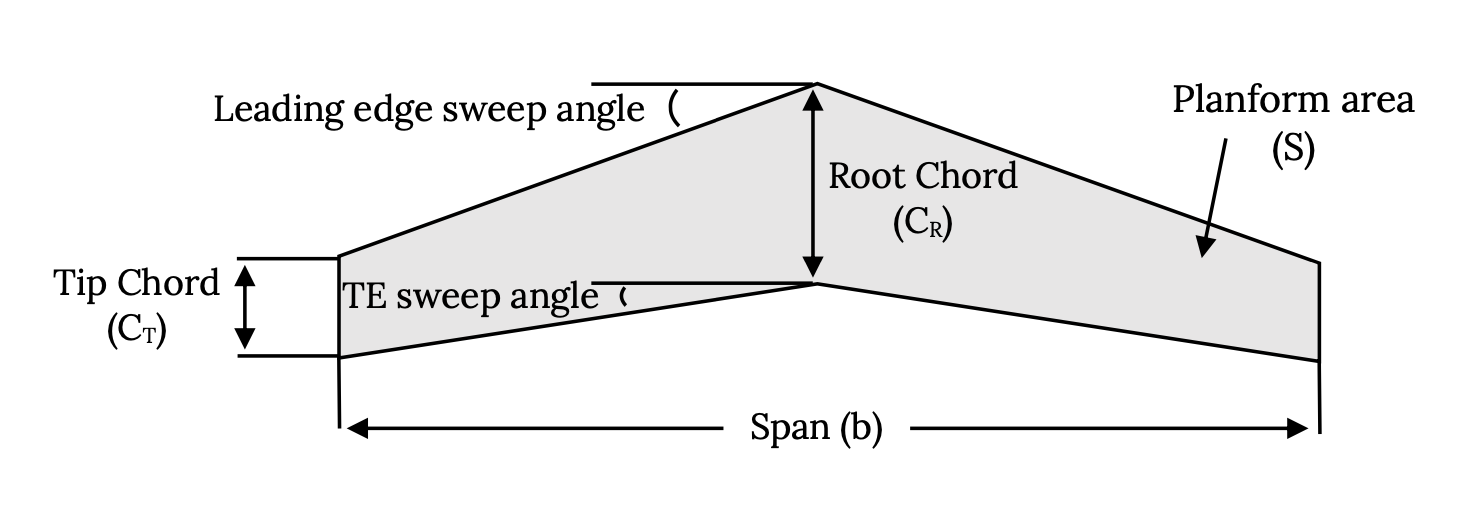
Прометане крило показано з заданою плоскою площею капелюшка S. Центр області має кореневу хорду, шапку C sub cap R, яка звужується до кінчика хорди, капелюшок C sub cap T. Область має проліт b, що позначає ширину від кінчика крила до кінчика крила. Передній край нахилений вниз від горизонталі кутом розгортки переднього краю, а задній край нахилений вниз від горизонталі кутом розгортки заднього краю. — Малюнок 1.2: Термінологія форми крила

Зверніть увагу, що плоска площа не є фактичною площею поверхні крила, а є «проектованою областю» або площею тіні крила. Також зауважте, що деякі з використовуваних абревіатур не є інтуїтивними; проліт, відстань від кінчика крила до кінчика крила (включаючи будь-яку ширину фюзеляжу) позначається b, а площинна площа задається символом «S» а не «А». Кути розгортки зазвичай задаються символом лямбда (λ).

Ще одне визначення, яке засноване на плананіформи крила, - це Aspect Ratio (AR).

АР = б ² /с.

Співвідношення сторін - це також проміжок, розділений на «середній» або середній акорд. Пізніше ми виявимо, що співвідношення сторін є мірою ефективності крила при дальньому польоті.

Форми форми крила можуть значно відрізнятися від одного типу літака до іншого. Винищувачі, як правило, мають низьке співвідношення сторін або короткі, стійкі крила, в той час як транспортні літаки великої дальності мають більш високі форми пропорцій крила, а вітрильники мають ще більш високі прольоти крил. Деякі крила змітаються, а інші ні. Деякі крила мають трикутну або «дельту» планаформи. Якщо хтось подивиться на останні 100 років дизайну крила, він побачить майже нескінченну різноманітність форм. Деякі форми походять від аеродинамічної оптимізації, а інші формуються для структурної вигоди. Деякі формуються так, як вони є для скритності, інші - для маневреності в пілотажному польоті, а інші просто для задоволення бажання їх дизайнера для гарного вигляду літака.

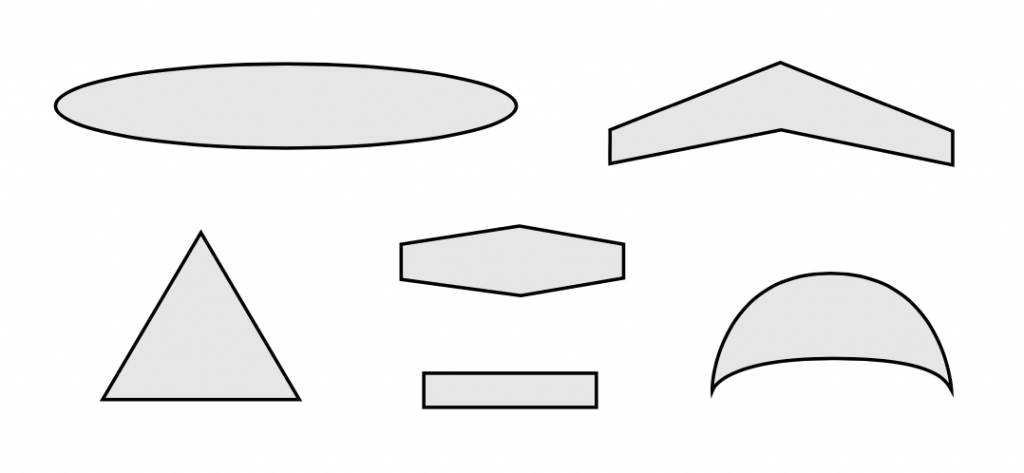
Прямокутне крило, представлене стандартним прямокутником, незмітається крило звуження від кореневої хорди до більш вузького кінчика хорди, стрілоподібне крило звуження від кореневої хорди до більш вузького кінчика хорди, дельта-крило, представлене у вигляді рівноцельного трикутника, еліптичне крило показано стандартним еліпсом, який ширше вона висока, форма півкола, при цьому горизонтальне дно замінено еліптичною нижньою лінією, схожою на товстий півмісяць. — Малюнок 1.3: Деякі форми форми крила

Загалом, крила з високим співвідношенням сторін бажані для літаків великої дальності, тоді як крила з меншим співвідношенням сторін дозволяють більш швидко реагувати на крени, коли маневреність є вимогою. Підмітання крила або вперед, або на кормі зменшить його опір, оскільки швидкість літака наближається до швидкості звуку, але також зменшить його ефективність на менших швидкостях. Дельта крила являють собою спосіб отримати поєднання високої розгортки і великої площі. Звуження крила, щоб надати йому нижчу хорду на кінчиках крила, як правило, дає дещо кращу продуктивність, ніж неконічне крило, а нелінійна конусність, яка дає «параболічну» планформу, теоретично дасть найкращу продуктивність.

У наступному матеріалі ми детальніше розглянемо деякі речі, згадані вище, та їх наслідки, пов'язані з льотною здатністю літака.

Перш ніж ми детальніше розглянемо аеродинаміку крила, ми спочатку розглянемо атмосферу, в якій повинен працювати літак, і розглянемо кілька основних взаємозв'язків, з якими ми стикаємося в «роблячи» аеродинаміку.

1.2 Повітря, наше середовище польоту

Літаки працюють у повітрі, газі, що складається з азоту, кисню та кількох інших складових. Поведінка повітря, тобто те, як його властивості, такі як температура, тиск і щільність, відносяться один до одного, можна описати рівнянням ідеального або ідеального газу стану:

$P = ρRT$

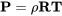
де P - барометричний або гідростатичний тиск, ρ - щільність, а T - температура. R - газова константа для повітря. У цьому рівнянні температура і тиск повинні бути вказані в абсолютних значеннях; іншими словами, температура повинна бути в Кельвіні або Ренкіні, а не за Цельсієм (за Цельсієм) або Фаренгейтом. Звичайно, всі одиниці повинні відповідати тим, що використовуються в газовій константі:

$Швидкість повітря = 1716.16 футів 2/сек 2r = 287,05 н−м/кгК$

1.3 Одиниці

Це підводить нас до теми одиниць. Важливо, щоб усі одиниці в ідеальному рівнянні газу були сумісні; тобто всі англійські одиниці або всі одиниці СІ, і щоб ми були обережні при вирішенні, наприклад, тиску, щоб переконатися, що одиниці тиску виходять як слід (фунти на квадратний фут в англійській системі або Паскаль в SI). На жаль, багато хто з нас не мають поняття про те, як працювати з одиницями.

У наукових колах США популярно намагатися переконати всіх, що американці є єдиними людьми у світі, які використовують «англійські» одиниці та єдині люди у світі, які не знають, як правильно використовувати одиниці СІ. Ніщо не може бути далі від істини. Ніхто в світі насправді не використовує одиниці СІ правильно в повсякденному житті. Наприклад, решта світу зазвичай використовує Кілограм як одиницю ваги, коли це фактично одиниця маси. Вони купують продукцію в продуктовому магазині в Кілограмах, а не ньютонах. Вам також буде важко знайти когось у світі, навіть у Франції, хто знає, що Паскаль - це одиниця тиску. Ньютони і Паскалі просто не використовуються в багатьох місцях поза підручниками. В Англії відстані на автомагістралі все ще даються в милі, а швидкість дається в миль/год, навіть коли люди вимірюють коротші відстані в метрах (або метрах), і уряд все ще намагається змусити людей перестати зважувати овочі в фунтах. В Англії є багато людей, які до сих пір віддають свою вагу в «камені».

Як аерокосмічні інженери, ми виявимо, що, незважаючи на те, що говорять багато наших підручників, більшість робіт у галузі виконується в англійській системі, а не SI, а деякі з них навіть не робляться у відповідних англійських одиницях. Швидкість літака вимірюється в милі на годину або в вузлах, а відстані часто вказуються в морських милі. Тиск дається пілотам в дюймах ртутного стовпа або в мілібарах. Тиск всередині реактивних і ракетних двигунів зазвичай вимірюється в фунтах на квадратний дюйм (psi). Висоти літака найчастіше цитуються в футах. Потужність двигуна дається в кінських силах і тяга в фунтах. Ми повинні вміти працювати в реальному світі, а також у політкоректному світі середньої школи чи коледжу фізики чи хімії або навіть інженерного тексту.

Слід зазначити, що те, що ми в Америці називаємо «англійською» системою одиниць, люди в Англії називають «імперськими» одиницями. Це може стати дійсно заплутаним, оскільки «імперські» ліквідні заходи відрізняються від «американських» рідинних заходів. «Імперський» галон трохи більший за американський галон, а «пінта» пива в Британії не має такого ж розміру, як «пінта» пива в США

Отже, існує безліч можливих систем одиниць, що використовуються в нашому світі. До них відносяться система СІ, англійська система на основі фунтів маси, англійська система, заснована на «слимаку», cgs-метрична система та інші. Ми можемо обговорити все це з точки зору дуже знайомого рівняння, старого доброго Ісаака Ньютона F = ма. Закон Ньютона пов'язує одиниці, а також фізичні властивості, і ми можемо використовувати його для розгляду декількох загальних систем одиниць.

Сила = маса х прискорення

1 Ньютон = 1 кг х 1 метр/сек ²

1 фунт сили = 1 фунт маси х 32.17 фут/сек ²

1 дин = 1 грам х 1 см/сек ²

1 фунт сили = 1 слимак х 1 фут/сек ²

Перше і останнє з перерахованого вище - це системи, з якими нам потрібно бути досконально знайомими; перша, тому що це «ідеальна» система, згідно з більшістю в науковому світі, і остання тому, що це напівофіційна система світу аерокосмічної техніки.

У використанні будь-якої системи агрегату є три основні вимоги:

Завжди записуйте одиниці з будь-яким числом, яке має одиниці.
Завжди працюйте через одиниці в рівняннях в той же час, коли ви розробляєте числа.
Завжди зменшуйте кінцеві одиниці до найпростішої форми та переконайтеся, що вони є відповідними одиницями для цього числа.

Після наведених вище пропозицій усуне близько половини неправильних відповідей, знайдених на більшості студентських домашніх завдань та тестових робіт.

При виконанні інженерних завдань слід проводити через одиниці, як описано вище, і переконатися, що одиниці мають сенс для відповіді і що величина відповіді є розумною. Хороші студенти роблять це постійно, а бідні залишають все на волю випадку.

Перша частина цього проста. Якщо одиниці у відповіді не мають сенсу, наприклад, якщо швидкість для літака розрахована на 345 футів на фунт або якщо ми обчислюємо вагу 1500 кілограмів в секунду, повинно бути легко визнати, що щось не так. Фундаментальна помилка була зроблена при дотриманні проблеми з одиницями, і це потрібно виправити.

Складніше завдання - розпізнати, коли величина відповіді неправильна; тобто не «в правильному бальному парку». Якщо нам кажуть, що швидкість автомобіля становить 92 метрів/сек. або 125 футів/сек. чи є у нас якесь «відчуття», чи є вони розумними чи ні? Це машина перевищує швидкість чи ні? Більшість з нас не мають поняття, не роблячи деяких швидких розрахунків (це 205 миль/год і 85 миль/год відповідно). Хто-небудь з нас знає свою вагу в Ньютоні? Що таке розумне барометричний тиск в атмосфері в будь-якій системі агрегату?

Отже, наше друге завдання, пов'язане з одиницею, полягає в тому, щоб розвинути деяку оцінку «нормального» діапазону величин для речей, які ми хочемо обчислити в обраній нами системі одиниць. Який розумний діапазон для коефіцієнта підйому крила або коефіцієнта опору? Чи розумно для автомобілів мати в 10 разів більший коефіцієнт опору літаків?

Маючи на увазі ці застереження, давайте повернемося назад і подивимося на наше «робоче середовище», стандартну атмосферу.

1.4 Стандартна атмосфера

Ми сказали, що ми починаємо з ідеального газового рівняння стану, P = RT. Ми також скористаємося гідростатичним рівнянням, ще одним зв'язком, який ви бачили раніше в хімії та фізиці:

$ΔP = −ρGΔH$

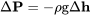
Це говорить нам про те, як змінюється тиск з висотою в стовпі рідини. Це говорить нам про те, як змінюється тиск, коли ми рухаємося вгору або вниз через атмосферу.

Ці два рівняння, рівняння стану ідеального газу та гідростатичне рівняння, мають три змінні; тиск, щільність та температура. Для вирішення цих властивостей в будь-якій точці атмосфери потрібно мати ще одне рівняння, одне з яких включає температуру. Це вимагатиме нашого першого припущення. Ми повинні мати певні стосунки, які можуть сказати нам, як температура повинна змінюватися залежно від висоти в атмосфері.

Багаторічні вимірювання та спостереження показали, що загалом нижню частину атмосфери, де літають більшість літаків, можна змоделювати у двох сегментах, Тропосфері та Стратосфері. Виявлено, що температура в тропосфері падає досить лінійно зі збільшенням висоти. Це лінійне зниження температури триває приблизно до 36 000 футів (близько 11 000 метрів). Вище цієї висоти температура тримається постійною до висот понад 100 000 футів. Ця область постійної температури є нижньою частиною стратосфери. Тропосфера і стратосфера - це місце, де працюють літаки, тому нам потрібно детально розглянути їх.

1.5 Тропосфера

Моделюємо лінійне падіння температури з висотою в тропосфері простим рівнянням:

T _alt = T _рівень _моря — Lh

де «L» називається «швидкістю лапсу». З більш ніж ста років вимірювань було встановлено, що нормальна середня частота затримки становить:

Л = 3,56 ^о Р/1000 футів = 6,5 ^о К/1000 метрів.

Цьому часто вчать пілотів у дивній суміші одиниць як 1.98 градусів за Цельсієм на тисячу футів!

Інше, що нам потрібно, - це значення температури рівня моря. Наша модель, також заснована на середніх за роки вимірювання, використовує наступні значення рівня моря для тиску, щільності та температури.

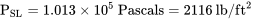
$PSL = 1.013×105 Паскаль = 2116 фунтів/фут 2$

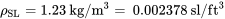
$ρ сл = 1,23 кг/м3 = 0,002378 сл/фут 3$

Т _СЛ = 288 ^о К = 520 ^о Р

Отже, для знаходження температури в будь-якій точці тропосфери використовуємо:

Т (^о Р) = 520 - 3,56 (ч),

де h - висота в тисячах футів, або

Т (^о К) = 288 - 6,5 (ч)

де h - висота в тисячах метрів.

На цьому етапі ми повинні підкреслити, що ця температурна модель для Тропосфери є лише моделлю, але це модель, яку всі в авіаційному та аерокосмічному співтоваристві погодилися прийняти та використовувати. Шанс коли-небудь поїхати на берег моря і виміряти температуру 59 ^o F тонкий, і навіть якщо ми виявимо, що температура вона неодмінно зміниться протягом декількох хвилин. Так само, якби ми відправили термометр вгору на повітряній кулі в будь-який день, шанс знайти «швидкість затримки», рівну тій, яка визначена як «стандарт», є тонкою, і під час проходження погодного фронту ми можемо навіть виявити, що температура збільшується, а не падає, коли ми рухаємось на більш високі висоти. Проте, ми будемо працювати з цією моделлю і, можливо, пізніше навчимося вносити корективи для нестандартних днів.

Тепер, якщо ми готові прийняти модель вище для зміни температури в Тропосфері, все, що нам потрібно зробити, це знайти відносини, щоб розповісти, як змінюються інші властивості, тиск і щільність з висотою в Тропосфері. Почнемо з диференціальної форми гідростатичного рівняння і об'єднаємо його з рівнянням Perfect Gas для усунення члена щільності.

$ДП=−ρ ГДГ, Р = ρ рт$

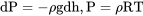
або,

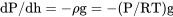
$ДП/ДГ = −ρG = − (P/RT) г$

який переставляється, щоб дати

ДП/р = — (г/рт) дх.

Тепер підставляємо в співвідношенні швидкості проміжку для температури, щоб отримати

ДП/р = {g/ [R (Т _СЛ -Lh)]} дх.

Тепер це зв'язок лише з однією змінною (P) зліва та лише однією (h) праворуч. Він може бути інтегрований, щоб дати

$Палт/PSL = [Талт/TSL] г/LR$

Аналогічним чином ми можемо отримати зв'язок, щоб знайти щільність на будь-якій висоті в тропосфері.

$ρ алт/ρ сл = [тал/ТСл] (G−LR) /LR$

Отже, тепер у нас є рівняння, щоб знайти тиск, щільність і температуру на будь-якій висоті в тропосфері. При використанні цих рівнянь слід дотримуватися обережності з одиницями. Всі температури повинні бути в абсолютних значеннях (Кельвін або Ренкін замість Цельсія або Фаренгейта). Показники в рівняннях співвідношення тиску та щільності повинні бути безодиничними. Експоненти не можуть мати одиниць!

Ми можемо використовувати ці рівняння до вершини Тропосфери, тобто до 11 000 метрів або 36 100 футів у висоту. Над цією висотою знаходиться Стратосфера, де температура моделюється як постійна приблизно до 100 000 футів.

1.6 Стратосфера

Ми можемо використовувати результат рівняння швидкості проміжку температури на висоті 11 000 метрів, щоб знайти температуру в цій частині Стратосфери.

Т _{стратосфера} = 216,5 ^о К = 389,99 ^о R = постійна

Рівняння визначення тиску і щільності в постійній температурній частині стратосфери відрізняються від рівнянь в тропосфері, оскільки температура постійна. І, оскільки температура постійна, і тиск, і щільність змінюються однаково.

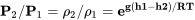
$Р2/Р1 = ρ2/ρ1 = наприклад (h1−h2) /РТ$

Термін праворуч у рівнянні - «e» або 2.718, оцінений відповідно до показаної потужності, де h ₁ - 11,000 метрів або 36,100 футів (залежно від використовуваної одиничної системи), а h ₂ - висота, на якій слід розрахувати тиск або щільність. T - температура в стратосфері.

Використовуючи наведені вище рівняння, ми можемо знайти тиск, температуру або щільність в будь-якому місці літака може літати. Цю інформацію прийнято табулювати в стандартну таблицю атмосфери. Більшість таких таблиць також включають швидкість звуку і в'язкість повітря, обидві з яких є функціями температури. Таблиці як в SI, так і в англійській одиницях наведені нижче.

Таблиця 1.1: Стандартна атмосфера в одиницях СІ

ч (км)	Т (градуси С)	а (м/ сек)	Px10^ (-4) (Н/м ^ 2) (паскалі)	P (кг/м ^ 3)	u x10 ^ 5 (кг/м сек)
0	15	340	10.132	1.226	1.78
1	8.5	336	8.987	1.112	1.749
2	2	332	7,948	1.007	1.717
3	-4.5	329	7.01	0.909	1.684
4	-11	325	6.163	0.82	1,652
5	-17,5	320	5.4	0,737	1.619
6	-24	316	4.717	0.66	1.586
7	-30.5	312	4.104	0,589	1.552
8	-37	308	3.58	0.526	1.517
9	-43.5	304	3.073	0,467	1.482
10	-50	299	2.642	0,413	1.447
11	-56.5	295	2.261	0,364	1.418
12	-56.5	295	1.932	0,311	1.418
13	-56.5	295	1.65	0,265	1.418
14	-56.5	295	1.409	0,227	1.418
15	-56.5	295	1.203	0,194	1.418
16	-56.5	295	1.027	0.163	1.418
17	-56.5	295	0,785	0.141	1.418
18	-56.5	295	0,749	0,121	1.418
19	-56.5	295	0,64	0.103	1.418
20	-56.5	295	0.546	0,088	1.418
30	-56.5	295	0,117	0.019	1.418
45	40	355	0,017	0,002	1.912
60	70.8	372	0,003	0.00039	2.047
75	-10	325	0.0006	0,00008	1,667

Таблиця 1.2: Стандартна атмосфера в англійських одиницях

ч (фути)	Т (градуси F)	a (фут/сек)	р (фунт/фут ^ 2)	р (слимаки/фут ^ 3)	u х 10 ^ 7 (сл/фут-сек)
0	59	1117	2116.2	0,002378	3.719
1 000	57.44	1113	2040.9	0,00231	3.69
2 000	51.87	1109	1967.7	0,002242	3.679
3 000	48.31	ll05	1896.7	0,002177	3.659
4 000	44.74	ll02	1827.7	0.002112	3.639
5 000	41.18	1098	1760,8	0.002049	3.618
6 000	37.62	1094	1696	0.001988	3.598
7 000	34.05	1090	1633	0,001928	3.577
8 000	30.49	1086	1571.9	0,001869	3.57
9 000	26.92	1082	1512.9	0.001812	3.536
10 000	23.36	1078	1455.4	0,001756	3.515
л,000	19.8	1074	1399.8	0,001702	3.495
12 000	16.23	1070	1345,9	0,001649	3.474
13 000	12.67	1066	1293.7	0,001597	3.453
14 000	9.1	1062	1243.2	0,001546	3.432
15 000	5.54	1058	1194.3	0,001497	3.411
16 000	1.98	1054	1147	0,001448	3.39
17 000	-1.59	1050	1101.1	0.001401	3.369
18 000	-5.15	1046	1056.9	0,001355	3.347
19 000	-8.72	1041	1014	0,001311	3.326
20 000	-12.28	1037	972.6	0.001267	3.305
21 000	-15.84	1033	932.5	0,001225	3.283
22 000	-19.41	1029	893.8	0,001183	3.262
23 000	-22.97	1025	856.4	0,001143	3.24
24 000	-26.54	1021	820.3	0,001104	3.218
25 000	-30.1	1017	785.3	0,001066	3.196
26 000	-33.66	1012	751.7	0,001029	3.174
27 000	-37.23	1008	719.2	0.000993	3.153
28 000	-40.79	1004	687.9	0.000957	3.13
29 000	-44.36	999	657.6	0,000923	3.108
30 000	-47.92	995	628.5	0,00089	3.086
31 000	-51.48	991	600,4	0.000858	3.064
32 000	-55.05	987	573.3	0.000826	3.041
33 000	-58.61	982	547,3	0.000796	3.019
34 000	-62.18	978	522.2	0.000766	2.97
35 000	-65.74	973	498	0.000737	2.974
40 000	-67.6	971	391.8	0.0005857	2.961
45 000	-67.6	971	308	0.0004605	2.961
50 000	-67.6	971	242.2	0.0003622	2.961

Таблиця 1.2: Стандартна атмосфера в англійських одиницях (con't)

ч (фути)	Т (градуси F)	a (фут/сек)	р (фунт/фут ^ 2)	р (слимаки/фут ^ 3)	u х 10 ^ 7 (сл/фут-сек)
60 000	-67.6	971	150.9	0.000224	2.961
70 000	-67.6	971	93.5	0.0001389	2.961
80 000	-67.6	971	58	0.0000861	2.961
90 000	-67.6	971	36	0,0000535	2.961
100 000	-67.6	971	22.4	0,0000331	2.961
150 000	113,5	1174	3.003	0.00000305	4.032
200 000	159.4	1220	0.6645	0.00000062	4.277
250 000	-8.2	1042	0.1139	0,00000015	3.333

Погляд на ці таблиці покаже пару термінів, які ми не обговорювали. Це і швидкість звуку «а», і в'язкість «μ». Швидкість звуку є функцією температури і зменшується при зниженні температури в Тропосфері. В'язкість також є функцією температури.

Швидкість звуку - це міра «стисливості» рідини. Вода досить нестислива, але повітря може бути стиснутий так, як це може бути в системі поршня/циліндра. Швидкість звуку по суті є мірою того, наскільки швидко звук або хвиля стиснення можуть рухатися через рідину. Ми часто говоримо про швидкості високошвидкісних літаків з точки зору числа Маха, де число Маха - це залежність між швидкістю польоту і швидкістю звуку. Коли ми наближаємося до швидкості звуку (Mach One), повітря стає більш стисливим, і стає більш значущим писати багато рівнянь, які описують потік з точки зору числа Маха, а не з точки зору швидкості.

В'язкість - це міра ступеня, до якої молекули рідини натикаються один в одного і переносять сили на мікроскопічному рівні. Це стає мірою «тертя» всередині рідини і є важливим терміном при погляді на опір тертя, опір через сили зсуву, які виникають, коли рідина (повітря в нашому випадку) рухається по поверхні крила або тіла в потоці.

У цих таблицях слід зазначити дві речі про в'язкість. По-перше, одиниці виглядають як би дивно. По-друге, колона в'язкості очолюється μ X 10 ^х. Одиниці належні для в'язкості в SI та англійській системах відповідно; однак, якщо ви поговорите з хіміком або фізиком про в'язкість, вони, ймовірно, цитуватимуть числа з одиницями «врівноваженості». Число 10 ^x у заголовку стовпця означає, що число, показане у стовпці, було помножено на 10 ^x, щоб дати йому показане значення. Це, для більшості з нас, не інтуїтивно. Це означає, що в англійській одиничній версії таблиці Standard Atmosphere в'язкість на рівні моря має значення 3,719 разів десять до мінус 7.

Так що тепер ми можемо знайти властивості повітря на будь-якій висоті в нашій моделі або «стандартній» атмосфері. Однак це лише модель, і було б рідко знайти день, коли атмосфера насправді відповідає нашій моделі. Наскільки це корисно?

Насправді ця модель досить хороша, коли мова йде про зміну тиску в атмосфері, оскільки вона заснована на гідростатичному рівнянні, яке є фізично правильним. З іншого боку, тиск на рівні моря змінюється день у день із змінами погоди, оскільки проблемна область потрапляє під різні системи високого або низького тиску, які часто відзначаються на погодних картах. Температура являє собою найбільшу можливість для зміни між моделлю і реальною атмосферою, адже скільки днів на рік температура на пляжі 59 ^o F (520 ^o R)? Щільність, звичайно, є функцією тиску і температури, тому її «правильність» залежить від правильності P і T.

На перший погляд, здається, що Стандартна атмосфера - це дещо фантазія. З іншого боку, це дає нам досить гарне уявлення про те, як ці властивості повітря повинні нормально змінюватися з висотою. І, можливо, ми можемо внести виправлення до відповідей, знайдених при використанні цієї моделі, виправляючи фактичний тиск і температуру на рівні моря, якщо це необхідно. Крім того, ми могли б визначити інші «стандартні» атмосфери, якщо ми дивимося на умови польоту, де умови виключно відрізняються від цієї моделі. Це робиться для того, щоб надати моделі атмосфери «Арктичного мінімуму» і «Тропічного максимуму».

Зрештою, ми робимо всі показники літаків та аеродинамічні розрахунки на основі нормальної стандартної атмосфери, і всі льотні випробування проводяться в стандартних умовах атмосферного тиску для визначення висот. Стандартна атмосфера - наша модель і виявляється, що ця модель служить нам добре.

Один із способів використання цієї моделі - визначити нашу висоту в польоті.

1.7 Вимірювання висоти

Пілот літака повинен знати його висоту, і є кілька способів вимірювання висоти літака. Радар може бути використаний для вимірювання відстані літака над землею. Супутникові сигнали Global Positioning System можуть визначати положення літака, включаючи його висоту, в тривимірному просторі. Ці та деякі інші можливі методи визначення висоти залежать від роботи однієї або декількох електричних систем, і хоча ми можемо захотіти мати такий прилад на нашому літаку, нам також потрібно мати «висотомір», який не залежить від акумуляторів або генераторів для його роботи. Далі висота, яку потрібно знати пілоту, - це висота над рівнем моря. Очевидним рішенням є використання наших знань про те, що тиск змінюється досить надійно з висотою.

Якщо ми знаємо, як тиск змінюється в залежності від висоти, то ми можемо виміряти цей тиск і визначити висоту над контрольною точкою рівня моря. Іншими словами, якщо ми виміряємо тиск як 836 фунтів на квадратний фут, ми можемо заглянути в стандартну таблицю атмосфери і виявити, що ми повинні бути на висоті 23,000 футів. Отже, все, що нам потрібно зробити, це побудувати простий механічний барометр і відкалібрувати його циферблат так, щоб він читав в одиницях висоти, а не тиску. Зі зменшенням виміряного тиску зазначена висота збільшується відповідно до стандартної моделі атмосфери. Це, по суті, як «прості» висотометри, такі як ті, які іноді використовуються в автомобілі або велосипеди або навіть «ультралегкі» літаки. Барометр вимірює тиск повітря і на якомусь типі циферблата або шкали замість одиниць тиску вказуються еквівалентні висоти.

Однак «простий» висотомір може бути недостатньо точним для більшості польотів через зміни атмосферного тиску зі змінами погодної системи. Простий висотомір базуватиме свої показання на припущенні, що тиск на рівні моря становить 2116 psf. Якщо, однак, ми знаходимося в зоні «високого» тиску, висотомір літака, що сидить на рівні моря, відчував би більший за стандартний тиск і вказував на висоту трохи нижче рівня моря. І навпаки, поблизу атмосферної системи низького тиску висотомір буде зчитувати висоту вище фактичного значення. Якщо ця помилка була лише кілька футів, це може не мати значення, але насправді це може призвести до помилок у кілька сотень футів у показаннях висоти. Це може призвести до катастрофи в погану погоду, коли пілоту доводиться покладатися на висотомір, щоб переконатися, що літак очищає гірські вершини або наближається до злітно-посадкової смуги на потрібній висоті. Значить, всі літаки сьогодні використовують «чутливі» висотометри, які дозволяють пілоту налаштовувати прилад на зміни тиску через атмосферних погодних умов.

Чутливий висотомір, показаний на наступному малюнку, має ручку, яку можна повернути для регулювання показань приладу при нестандартних тисках рівня моря. Це може бути використано двома різними способами в польоті. Коли літак сидить на землі в аеропорту, пілот може просто відрегулювати ручку, поки висотомір не зчитує відому висоту аеропорту. У польоті пілот може прослуховувати оновлення звітів про погоду з сусідніх аеропортів, звіти, які будуть включати поточний рівень моря еквівалентний барометричний тиск, і повертати ручку, поки цифри в невеликому вікні на обличчі висотоміра не погодяться з заявленим тиском. Ці показання зазвичай даються в одиницях міліметрів ртутного стовпа, де 29,92 - це стандарт рівня моря. Регулювання показань у вікні до більш високого тиску призведе до зменшення показань висотоміра, а регулювання його нижче збільшить індикацію висоти. При правильному і своєчасному використанні цього регулювання хороший висотомір повинен бути точним в межах близько 50 футів.

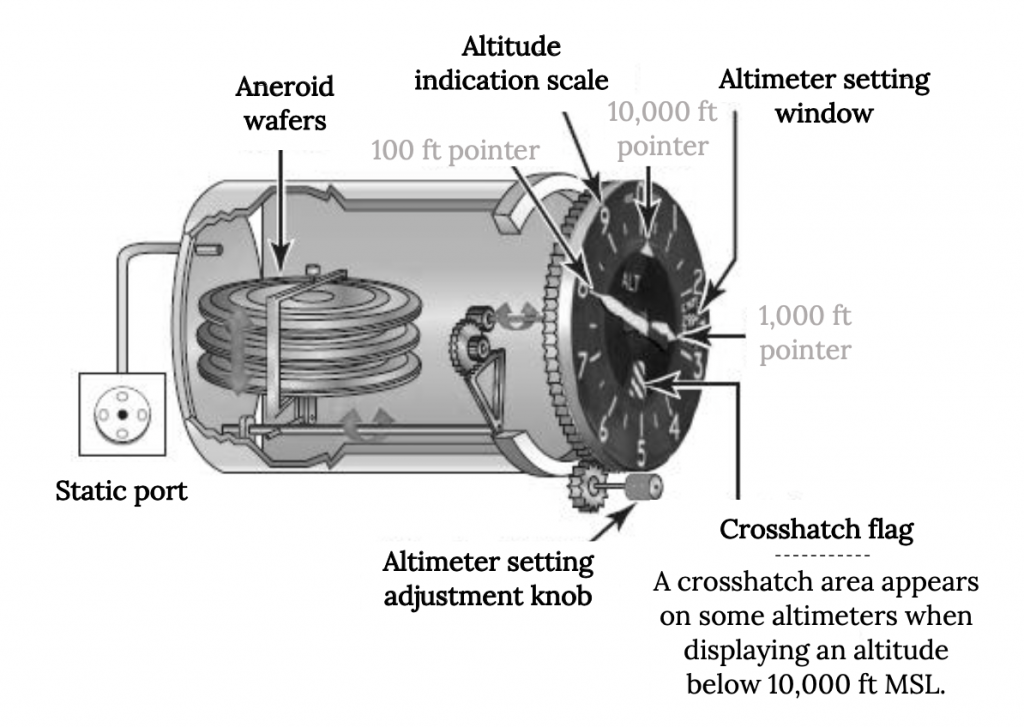
Повітря зі статичного порту надходить в камеру висотоміра, при цьому тиск призводить до того, що серія вертикальних анероїдних пластин розширюється або скорочується відповідно. Зсув пластини призводить до обертання горизонтального вала, який з'єднаний з сектором. Це призводить до того, що серія передач обертається для обертання центрального вала, з'єднаного з покажчиками в центрі альтімітера. На обличчі висотоміра невеликий білий трикутник позначає вказівник на 10 тисяч футів, тоді як коротка рука вказує на вказівник на 1 тисячу футів, а довша рука - вказівник на 100 футів. Цифри відображаються від 0 вгорі за годинниковою стрілкою навколо обличчя до 9 як шкала індикації висоти. Невеликий прапор перехрестя з'являється під точкою підключення покажчиків у центрі, щоб вказати висоти нижче 10 тисяч футів ковпачка M S L. Маленька ручка виставляється під висотоміром для його регулювання. — Малюнок 1.4: Типовий механічний чутливий висотомір

Слід зазначити, що ми також могли б використовувати щільність для визначення нашої висоти, і, насправді, це може виявитися більш значущим з точки зору зміни продуктивності літака на різних висотах польоту, оскільки тяга двигуна і потужність, як відомо, є функціями щільності та аеродинамічного підйому та опору. є також функціями щільності. Однак для «вимірювання» щільності буде потрібно вимірювання як тиску, так і температури. Це може призвести до більшої помилки у використанні стандартної атмосфери для визначення висоти, ніж використання лише тиску, оскільки коливання температури набагато більше схильні до нестандартної поведінки, ніж тиск. З іншого боку, ми іноді вважаємо цінним обчислити нашу «висоту щільності», дивлячись на здатність літака злітати на заданій відстані землі.

Якщо ми знаходимося в аеропорту, який знаходиться на висоті, скажімо, 4000 футів, а температура вище, ніж 44.74 ^o F, передбачена стандартною атмосферою (як це, ймовірно, було б влітку), ми виявимо, що літак поводиться так, ніби він знаходиться на більшій висоті і займе більшу відстань. щоб стати повітряно-крапельним, ніж це повинно на 4000 футів. Пілоти використовують або круговий калькулятор типу правила ковзання, або спеціальний електронний калькулятор, щоб взяти виміряну реальну температуру та поєднати її з висотою тиску, щоб знайти «висоту щільності», і це може бути використано для оцінки додаткової відстані зльоту, необхідної відносно стандартних умов.

Деякі можуть задатися питанням, чому ми не можемо просто використовувати температуру, щоб знайти нашу висоту. Зрештою, чи не було одним з наших основних припущень, що в Тропосфері температура падала лінійно з висотою? Чи не було б дуже легко засунути термометр у вікно і порівняти його читання зі стандартною діаграмою атмосфери, щоб знайти нашу висоту?

Звичайно, як тільки ми знаходимося над Тропосферою, це не принесе користі, оскільки температура стає постійною на висоті тисячі футів, але чому б це не працювати в Тропосфері?

Думка вправа

Подумайте і обговоріть, чому використання температури для пошуку висоти не є гарною ідеєю.
Чому тиск - найкраща властивість вимірювати, щоб знайти нашу висоту?
Можливо, використання щільності для пошуку висоти було б кращою ідеєю, оскільки щільність безпосередньо впливає на продуктивність польоту. Подумайте про одну причину, чому у нас немає висотометрів, які вимірюють щільність повітря.

1.8 Рівняння Бернуллі

Ви, безсумнівно, були знайомі з відносинами під назвою Рівняння Бернуллі або Принцип Бернуллі десь у попередньому курсі фізики чи хімії. Це принцип, який пов'язує тиск зі швидкістю в будь-якій рідині, по суті показуючи, що зі збільшенням швидкості рідини її тиск зменшується і навпаки. Цей принцип може приймати кілька різних математичних форм в залежності від рідини і її швидкості. Для нестисливої рідини, такої як вода або для повітря нижче приблизно 75% швидкості звуку це співвідношення набуває такого вигляду:

Р + ½ ρ В ² = П ₀

(гідро) статичний тиск+динамічний тиск = загальний тиск

[внутрішня енергія+кінетична енергія = загальна енергія]

Цей зв'язок може розглядатися або як міра балансу сил тиску в потоці, або як енергетичний баланс (перший закон термодинаміки), коли немає змін потенційної енергії або теплопередачі.

Рівняння Бернуллі говорить, що вздовж будь-якого безперервного шляху («обтічної лінії») у потоці загальний тиск, P ₀, (або загальна енергія) зберігається (постійна) і є сумою статичного тиску та динамічного тиску в потоці. Статичний тиск і динамічний тиск можуть як змінюватися, але вони повинні змінюватися таким чином, щоб їх сума була постійною; тобто в міру прискорення потоку тиск зменшується.

* A ПРИПУЩЕННЯ: Дуже важливо, щоб ми знали і розуміли припущення, які обмежують використання цієї форми рівняння Бернуллі. Рівняння може бути отримане або з першого закону термодинаміки (енергозбереження), або з балансу сил у рідині через те, що відоме як рівняння Ейлера. При отриманні форми рівняння вище робляться деякі припущення для того, щоб зробити деякі математики простішими. Вони включають такі речі, як припущення, що щільність є постійною, що робить її постійною на етапі інтеграції у виведенні та полегшує інтеграцію. Також передбачається, що маса зберігається, здавалося б, логічне припущення, але таке, яке має певні наслідки у використанні рівняння. Також передбачається, що потік «стійкий», тобто швидкість в будь-якій точці потоку не змінюється з часом. Інший спосіб сказати це полягає в тому, що швидкість може змінюватися залежно від положення в потоці (це насправді те, про що рівняння), але не може змінюватися з часом.

Припущення про постійну щільність, яку ми зазвичай називаємо припущенням нестисливого потоку, означає, що ми повинні дотримуватися обмеження швидкості. Коли повітря прискорюється і швидкість наближається до швидкості звуку, його щільність змінюється; тобто стає стисливою. Отже, коли наші швидкості потоку наближаються до швидкості звуку, припущення про нестисливе потоку порушується, і ми більше не можемо використовувати цю форму рівняння Бернуллі. Коли це стає проблемою?

Деякі підручники з механіки рідини використовують математичне співвідношення рядів, щоб подивитися на взаємозв'язок між швидкістю або числом Маха (число Маха, швидкість, розділена на швидкість звуку, дійсно кращий показник стисливості, ніж швидкість поодинці), і вони використовують це, щоб показати, що припущення нестисливого потоку є не діє вище числа Маха приблизно в 0,3 або 0,3 рази більше швидкості звуку. Це хороша математика, але не така хороша фізика. Важливим є не те, як працює математика, а те, як взаємозв'язок між двома тисками в рівнянні Бернуллі змінюється зі збільшенням швидкості або числа Маха. Ми розглянемо це в наступному прикладі, щоб показати, що ми насправді досить безпечні у використанні нестисливої форми рівняння Бернуллі до приблизно 75% швидкості звуку.

Іншими важливими припущеннями в цій формі рівняння Бернуллі є припущення стійкого потоку та збереження маси. Стійкий потік означає майже те, що він звучить; рівняння здатне враховувати лише зміни швидкості та тиску з положенням у полі потоку. Передбачалося, що потік точно такий же в будь-який час.

Припущення про збереження маси дійсно стосується розгляду того, що називається «обтічними лініями» у потоці. Їх можна розглядати на базовому рівні як шляхи потоку або магістралі, які слідують або окреслюють рух потоку. Збереження маси означає, що в будь-якій точці уздовж цих шляхів або між будь-якими двома обтічними потоками масовий потік між обтічними лініями (на шляху) такий же, як і в будь-якій іншій точці між тими ж двома обтічними лініями (або по тому ж шляху).

Кінцевим результатом цього припущення збереження маси є те, що рівняння Бернуллі гарантовано тримається вірним лише уздовж обтічної лінії або шляху в потоці. Однак ми можемо розширити використання співвідношення до будь-якої точки потоку, якщо весь потік вздовж усіх обтічних ліній (або шляхів) у певній контрольній точці вище за течією (при «∞») має однакову загальну енергію або загальний тиск.

Отже, ми можемо використовувати рівняння Бернуллі, щоб пояснити, як крило може виробляти підйом. Якщо потік над верхньою частиною крила швидше, ніж над нижнім, тиск на верхній буде менше, ніж на нижній і результуюча різниця тисків буде виробляти підйом. Вивчення аеродинаміки дійсно все про прогнозування таких змін швидкості і тиску навколо різних форм крил і тіл. Аеродинаміки пишуть рівняння, щоб описати спосіб зміни швидкості повітря навколо заданих форм, а потім поєднують їх з рівнянням Бернуллі, щоб знайти отримані тиск і сили.

Давайте подивимося на використання рівняння Бернуллі для наведеного нижче випадку крила, що рухається по повітрю на 100 метрів/сек. на висоті 1 км.

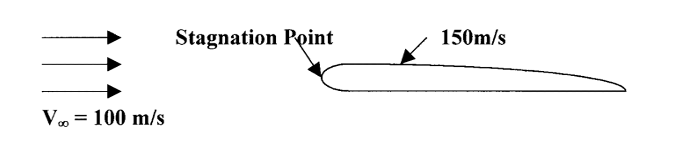
Повітря наближається до аеропрофілю з горизонтальною кришкою швидкості V sub нескінченності 100 метрів в секунду. Сама пряма точка аеропрофілю - точка застою, а швидкість в точці однієї третини шляху через верхню поверхню становить 150 метрів в секунду. — Малюнок 1.5: Приклад рівняння Бернуллі

Ми хочемо знайти тиск на передньому краї крила, де потік приходить в спокій (точка застою) і в точці над крилом, де швидкість прискорилася до 150 м/с.

По-перше, зверніть увагу, що корпус крила, що рухається по повітрю, був зображений як одне з нерухомого крила з повітрям, що рухається повз нього з потрібною швидкістю. Це стандартна процедура в робочих задачах аеродинаміки, і можна показати, що відповіді, які можна знайти за допомогою цього методу, є правильними. По суті, оскільки процес використання рівняння Бернуллі є одним із поглядів на збереження енергії, не має значення, чи ми аналізуємо рух (кінетичну енергію), що бере участь як рух тіла чи рух рідини.

Тепер давайте подумаємо над проблемою, представленою вище. Ми знаємо щось про потік у трьох точках:

Ну і перед крилом у нас є те, що називається «вільний потік» або непорушений, рівномірний потік. Ми позначаємо властивості в цьому потоці з індексом нескінченності [∞]. Ми можемо записати рівняння Бернуллі тут як:

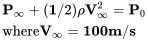
$Р+ (1/2) ρv₂ 2 = p0 де V∞ = 100 м/с$

Зверніть увагу, що саме в цей момент «вільний потік», де весь потік рівномірний і має однакову сумарну енергію. Якщо в цей момент потік не був рівномірним, можливо, тому, що він знаходився поблизу землі і швидкість збільшується з відстанню від землі, ми не могли припустити, що кожна «обтічна лінія» має різне значення загального тиску (енергії).

У передній частині крила у нас буде точка, де потік прийде відпочивати. Ми називаємо цю точку «точкою стагнації», якщо можна припустити, що потік сповільнився і зупинився без істотних втрат. Тут швидкість потоку дорівнювала б нулю. Ми можемо записати рівняння Бернуллі тут як:

P _{стагнація} + 0 = P ₀

У цей момент потік прискорився до 150 м/с, і ми можемо записати рівняння Бернуллі як:

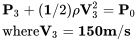
$Р3+ (1/2) ρ В32 = Р 0 де V3 = 150 м/с$

Тепер ми знаємо, що оскільки потік над крилом безперервний (маса зберігається), загальний тиск (P ₀ ) однаковий у всіх трьох точках, і саме це ми використовуємо для пошуку відсутньої інформації. Для цього ми повинні зрозуміти, який із цих тисків (якщо такий є) відомий нам як атмосферний гідростатичний тиск, і зрозуміти, що ми можемо припустити, що щільність постійна до тих пір, поки ми безпечно нижче швидкості звуку.

Спочатку ми знаємо, що тиск в атмосфері таке, що в стандартній таблиці атмосфери для висоти 1 км або 89870 Паскалей і що щільність на цій висоті становить 1,112 кг/м ³. Дивлячись на проблему, найбільш логічним місцем для застосування стандартних атмосферних умов є місце «вільного потоку», оскільки саме тут існує непорушений потік. Звідси

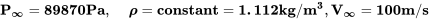
$P∞ = 89870Па, ρ = постійна = 1,112 кг/м3, V∞ = 100 м/с$

І, використовуючи їх у рівнянні Бернуллі у вільному місці потоку, ми обчислюємо загальний тиск.

Р ₀ = 95430 Па

Тепер, коли ми знайшли загальний тиск, ми можемо використовувати його в будь-якому іншому місці потоку, щоб знайти інші невідомі властивості.

У місці застою

Р _{стагнація} = Р ₀ = 95430 Па

У точці, де швидкість становить 150 м/с, ми можемо переставити рівняння Бернуллі, щоб знайти

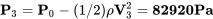
$Р3 = П0− (1/2) ρ В32 = 82920Па$

Як перевірку ми повинні підтвердити, що статичний тиск (P ₃) в цій точці менше, ніж статичний тиск вільного потоку (P), оскільки швидкість тут вища, а також підтвердити, що статичний тиск скрізь у потоці нижче, ніж тиск застою.

Тепер давайте розглянемо кроки в роботі будь-якої задачі з рівнянням Бернуллі. Спочатку ми повинні намалювати потік і записати все, що ми знаємо, в різних точках цього потоку. По-друге, ми повинні написати рівняння Бернуллі в кожній точці потоку, де ми або знаємо інформацію, або хочемо щось знати. По-третє, ми повинні ретельно оцінити, який тиск, якщо такий є, можна отримати зі стандартної таблиці атмосфери. По-четверте, ми повинні подивитися на всі ці точки потоку і побачити, яка точка дає нам достатньо інформації для вирішення загального тиску (P ₀). Нарешті, ми використовуємо це значення P ₀ у рівнянні Бернуллі в інших точках потоку, щоб знайти інші відсутні члени. Спроба пропустити будь-який з перерахованих вище кроків може призвести до помилок для більшості з нас.

Однією з найпоширеніших проблем, які виникають у людей при роботі з рівнянням Бернуллі в такій задачі, як наведена вище, є припустити, що точка застою є місцем для початку вирішення проблеми. Вони дивляться на три точки в потоці і припускають, що точка застою повинна бути тим місцем, де все відомо. Зрештою, хіба швидкість в точці стагнації не дорівнює нулю? Чи не означає це, що статичний тиск і загальний тиск тут однакові? І який ще висновок можна зробити, ніж припустити, що цей тиск повинен бути тоді атмосферним?

Ну, відповідь на перші два питання - «так», але третє «так» не слідує. Що відомо в точці стагнації, це те, що термін статичного тиску в рівнянні тепер є статичним тиском у точці стагнації і тому називається тиском стагнації. А, так як швидкість дорівнює нулю, тиск застою дорівнює загальному тиску в потоці. Жодне з цих тисків, однак, не є атмосферним тиском.

Чому тиск в місці застою не тиск в атмосфері? Ну, ось де наша заміна рухомого потоку і нерухомого крила для рухомого крила в нерухомій рідини закінчується викликаючи нам деяку плутанину. Насправді ця точка застою - це місце, де крило стикається лоб з повітрям, через яке воно мчить . Тиск тут, тиск застою, повинен дорівнювати тиску в атмосфері плюс тиск, викликаний зіткненням крила і рідини; тобто воно повинно бути вище атмосферного.

Наш підхід до моделювання потоку крила, що рухається через нерухому атмосферу як рухомий потік навколо нерухомого крила, полегшує роботу з рівнянням Бернуллі загалом; однак, ми повинні мати на увазі, що це заміщаюча модель і змінити наш спосіб перегляду на неї належним чином. У цій моделі гідростатичний тиск - це не той тиск, де повітря «статичний», це, скоріше, тиск, де потік «непорушений». Це в умовах «вільного потоку», точці вище за течією тіла (крило, в даному випадку), де потік ще не відчув присутності крила. Саме тут існує непорушена атмосфера. Між цією точкою та самим крилом потік повинен змінювати напрямок та швидкість, коли він рухається навколо тіла, тому ніде більше в полі потоку тиск не буде таким же, як у непорушеній атмосфері.

1.9 Вимірювання швидкості повітря

Тепер, коли ми знаємо щось про рівняння Бернуллі, ми можемо подивитися на інше використання зв'язку - вимірювання швидкості повітря. Переставляючи рівняння, ми можемо записати:

$V= [2 (Р0−П) /ρ] 1/2$

Отже, якщо ми знаємо загальний і статичний тиск у точці та щільність в цій точці, ми можемо легко знайти швидкість в цій точці. Все, що нам потрібно, це якийсь спосіб виміряти або іншим чином знайти ці величини.

Ми можемо знайти загальний тиск (P ₀), просто вставивши якусь відкриту трубку в потік, щоб вона була спрямована на зустрічний потік, а потім підключений до манометра якогось роду.

Загальний тиск вимірюється, коли повітря, що рухається на ковпачку V sub нескінченності, рухається безпосередньо через вирівняну трубку піто в закритий датчик на кінці. — Малюнок 1.6: Труба Піто вимірює загальний тиск

Статичний тиск можна знайти аналогічним чином, але потік повинен йти паралельно отворам у трубці або поверхні.

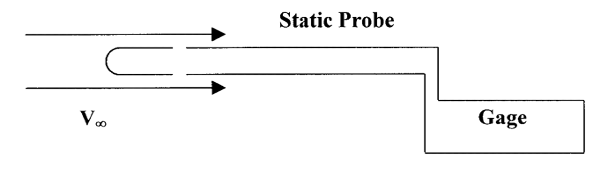
Статичний тиск вимірюється, коли повітря, що рухається на ковпачку V sub нескінченності, рухається повз отвору з боків статичного зонда, коли потім перетворюється нормально до потоку в датчик в кінці. — Малюнок 1.7: Статична трубка вимірює статичний тиск

На літаку ми зазвичай монтуємо трубку p itot десь на крилі або носі літака, де вона, як правило, вказуватиме на непорушений потік і не буде за гвинтом. Зчитування статичного тиску на літаку зазвичай приймається через отвір, розміщений у певній точці на боці літака, де потік матиме такий же статичний тиск, як потік вільного потоку замість використання окремого статичного зонда. Цей момент зазвичай визначається при льотних випробуваннях. Зазвичай є статичний порт по обидва боки площини, з'єднаний з однією трубкою через з'єднання «Т». Статичний порт виглядає як невелика кругла пластина з отвором в її центрі. Однією з завдань, необхідних пілоту в його або її передпольотному огляді літака, є переконатися, що як трубка Піто, так і статичні порти вільні від перешкод, особливо важливе завдання навесні року, коли комахи люблять повзати в невеликі отвори і будувати гнізда.

В аеродинамічній трубі та в інших експериментальних додатках ми часто використовуємо єдиний прилад для вимірювання як загального, так і статичного тиску. Цей прилад називається p itot-статичною трубкою, і це всього лише комбінація двох зондів, показаних вище.

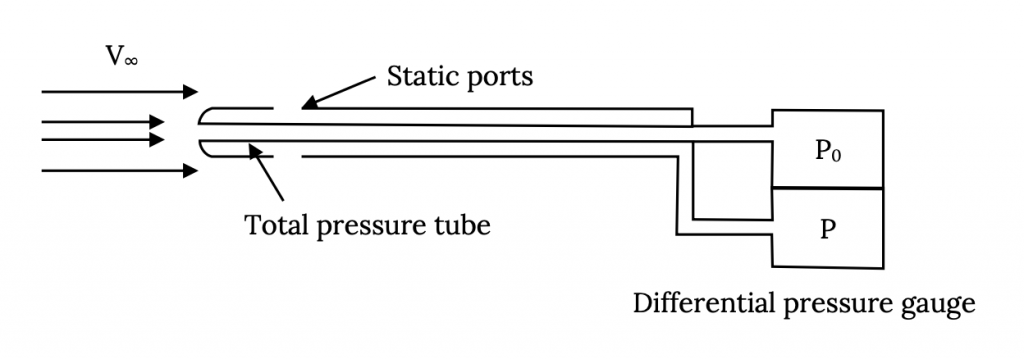
Піто-статичний зонд поєднує в собі попередні дві конфігурації, з одним отвором в центрі, вирівняним з потоком для загального тиску, і парою портів на зовнішній стороні закритої трубки, що оточують трубку загального тиску, щоб повітря протікало повз і вимірював тиск навколишнього середовища. Загальний тиск маркується як вузол ковпачка P, тоді як тиск навколишнього середовища маркується як ковпачок P, причому дві відповідні камери позначаються як датчик перепаду тиску. — Малюнок 1.8: Статичний зонд Піто

Як у лабораторному випадку, так і в корпусі літака це різниця в двох тисках, P ₀ - P, яку ми хочемо знати, і це можна виміряти за допомогою декількох різних типів пристроїв, починаючи від рідкого манометра «U-трубки» до складного електронного датчика. У літаку, де ми не хочемо, щоб наші знання швидкості повітря залежали від джерела електроенергії і де рідинний манометр був би громіздким, різниця тиску вимірюється механічним пристроєм, який називається анероїдним барометром.

Але давайте повернемося назад і подивимося на рівняння, яке використовується для пошуку швидкості і подивимося, чи це викликає якісь проблеми.

$V= [2 (Р0−П) /ρ] 1/2$

Це показує, що нам також потрібно знати щільність, якщо ми хочемо знайти швидкість. У лабораторії ми знаходимо щільність досить легко, вимірюючи барометричний тиск та температуру та обчислюючи щільність, використовуючи Закон ідеального газу,

$P = ρRT$

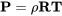
або,

$ρ = п/рт$

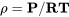
і, використовуючи це, ми можемо знайти точну або «справжню» швидкість повітря.

У літаку ми хочемо простоти та надійності, і хоча ми могли б попросити пілота чи якогось льотного комп'ютера виміряти тиск і температуру, потім обчислити щільність, а потім покласти її в рівняння Бернуллі для обчислення швидкості повітря, це здається трохи обтяжливим і, звичайно, використання комп'ютерів або калькуляторів може залежати від електрики. Отже, ми зазвичай не маємо приладу на літаку, який відображає справжню швидкість повітря; натомість ми вибираємо просто виміряти різницю в двох вищезазначених тисках за допомогою механічного інструменту, а потім калібрувати цей інструмент, щоб відобразити те, що ми називаємо вказаним irspeed, вимірювання швидкості, засноване на припущенні щільності рівня моря.

$Від = [2 (P0−P) /ρSL] 1/2$

Інша назва зазначеної швидкості - це «рівень моря еквівалент іршвидкості», швидкість, яка існувала б для виміряної різниці статичного та загального тиску, якщо літак знаходився на рівні моря.

Справжні і зазначені повітряні швидкості безпосередньо пов'язані квадратним коренем співвідношення рівня моря і справжніх щільностей.

$Vtrue=Вінд [ρSL/ρAlt] 1/2$

Потім індикатор швидкості повітря на літаку вимірює зазначену швидкість повітря, а не справжню швидкість польоту. Це герметичний прилад зі статичним тиском, що йде до ємності приладу, і загальним тиском, підключеним до анероїдного барометра всередині контейнера. Коли різниця в цих двох тисках змінюється, індикаторні голки на обличчі приладу рухаються по циферблату, відзначеному не для діапазону тисків, а для діапазону швидкостей. Кожен такий прилад ретельно калібрується, щоб забезпечити точне вимірювання зазначеної швидкості повітря.

Повітряне повітря потрапляє в трубку Піто, а потім відводиться через з'єднання піто у вертикальну діафрагму. Тиск повітря призводить до зміщення діафрагми в камері, тиск якої визначається з'єднаною з нею статичної повітряної магістраллю. Зсув діафрагми змушує центральний вал обертатися, а підключений важіль змушує сектор обертатися, а також. Потім це повертає шестерню ручної роботи, яка з'єднана з центром руки циферблата повітряної швидкості і повертає його, щоб дати пілоту вказівку на їх швидкість польоту. — Малюнок 1.9: Індикатор швидкості повітря

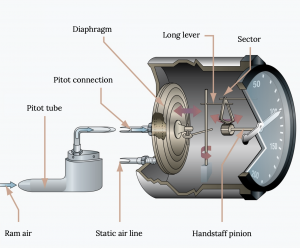
Отже, так само, як ми виявили, що висотомір на літаку вимірює неправильну висоту, якщо ми не зможемо її правильно відрегулювати, індикатор швидкості повітря не вимірює реальну швидкість повітря. Це проблема для нас?

Виявляється, що, що стосується продуктивності літака; тобто його здатність злітати на певну відстань, підніматися з певною швидкістю і т.д., насправді залежить від зазначеної швидкості польоту, а не від справжньої швидкості польоту. Так, ми хочемо знати справжню швидкість польоту, щоб знати, наскільки швидко ми дійсно їдемо і для відповідних цілей планування польоту, але наскільки знати швидкість, з якою слід обертатися при зльоті, найкращу швидкість, з якою підніматися або ковзати, і так далі, нам краще використовувати зазначену швидкість польоту.

Зазначена швидкість польоту, оскільки щільність вважається завжди умовами рівня моря, насправді є функцією лише різниці загального та статичного тисків, P ₀ - P, який ми знаємо з рівняння Бернуллі дорівнює:

$p0−p = 1/2 ρv2 = 1/2 ρl вінд 2 = 1/2 ρ алтв²2$

і ми збираємося виявити, що терміни праворуч, динамічний тиск, є дуже важливим терміном в обліку сил на тіло в рідині. Іншими словами, поведінка літака в польоті набагато більше залежить від динамічного тиску, ніж від однієї лише швидкості польоту.

Приклад: Давайте подивимося на різницю між істинною та вказаною швидкістю повітря, щоб отримати деяке уявлення про те, наскільки велика ця різниця може бути. Давайте виберемо висоту 15,000 футів і подивимося, якими будуть два значення швидкості повітря, якщо піто-статична система піддається різниці тиску 300 фунтів на квадратний фут (PSF). Щільність в стандартній атмосфері для 15000 футів становить 0,001497 сл/фут ³, тоді як на рівні моря 0,002378 сл/фут ³.

$Вітер = [2 (P0−P) /ρSL] 1/2 = 502 футів/сек$

$Vtrue=Вінд [ρSL/ρAlt] 1/2 = 633 футів/сек.$

Таким чином, різниця в цих двох показаннях може бути значною, але це нормально. Використовуємо зазначену швидкість польоту для польоту літака і використовуємо справжню швидкість польоту при знаходженні часу для поїздки. Зауважте, що при роботі з задачами рівняння Бернуллі, наприклад, при знаходженні варіацій тиску та швидкості навколо крила, ви завжди хочете використовувати справжню швидкість повітря та реальні тиски та щільність на висоті.

Нарешті, перебуваючи на тему швидкості польоту, слід зазначити, що, хоча ми часто обчислюємо швидкість літака або крила в одиницях футів/сек. або метрів/сек., Більшість показників швидкості повітря покаже швидкість повітря в одиницях або милі на годину або вузли. Вузол - це досить давня одиниця швидкості, яку використовували протягом століть моряки і колись виміряні, синхронізуючи вузлувату мотузку, як вона була опущена над бортом корабля в тече море.

Вузол - це морська миля на годину, а морська миля - це встановлена частка окружності землі. У відношенні до більш звичним англійським одиницям:

1 вузол (kt) = 1.15 миль/год

1 морська миля (нм) = 1,15 «статутних» миль (миль).

Це звичайна практика в усіх куточках світу, щоб наші політкоректні системи одиниць бути повністю ігноровані і робити все планування польоту і польоту з використанням одиниць вузлів і морських миль для швидкості і відстані.

1.10 Рівняння Бернуллі для стисливого потоку

Форма рівняння Бернуллі, яку ми використовували, призначена для нестисливого потоку, як було зазначено кілька разів. Що робити, якщо потік не є нестисливим?

Якби рівняння Бернуллі було виведено без припущення про постійну щільність повітря, воно вийшло б в іншій формі і було б залежністю між тисками та числом Маха. Відносини також мали б інший параметр у ньому, термін, який називається гамма (γ). Гамма - це просто число для даного газу, і число залежить від кількості атомів в молекулі газу, будь то одноатомний або двоатомний і т.д. повітря дійсно є сумішшю газів, але, загалом, він вважається двоатомним газом. Його значення гамма дорівнює 1,4.

[Інша назва гамма - це «співвідношення питомих нагрівань» або питома теплоємність при постійному тиску, розділена на питому теплоємність при постійній щільності. Ці питомі нагрівання є мірою способу передачі тепла в газі при певних обмеженнях (постійний тиск або щільність), і це, в свою чергу, залежить від молекулярного складу газу. У деяких інших областях, наприклад, термодинаміки, для цього співвідношення використовується буква «k» замість γ.]

Коли потік повинен вважатися стисливим, це співвідношення між тиском і швидкістю або число Маха набуває вигляду нижче:

(Р ₀ /Р) = {1 + [(γ-1) /2] М ²} ^[(γ-1)/(γ) ^]

Якщо використовувати як це рівняння, так і нестисливу форму рівняння Бернуллі для вирішення загального тиску для заданих швидкостей від нуля до 1000 футів/сек., використовуючи умови рівня моря і швидкість звуку на рівні моря знайти число Маха, пов'язане з кожною швидкістю, а потім порівняти стисливе і нестисливі значення загального тиску (P ₀) ви знайдете трохи більше 2% різниці при 700 футів/сек. і 5% при 900 футів/сек. Іншими словами, використання нестисливого рівняння Бернуллі для пошуку співвідношень тиску та швидкості є досить розумним до швидкості близько 75% швидкості звуку!

1.11 Сили в рідині

Вище було відзначено, що поведінка літака в польоті залежить від динамічного тиску, а не від швидкості або швидкості поодинці. Іншими словами, це певна комбінація щільності та швидкості, а не лише щільності чи швидкості, яка важлива для того, як літає літак чи ракета. Питання, яке можна задати, полягає в тому, чи існують інші комбінації властивостей рідини, які також мають великий вплив на аеродинамічні сили.

Ми вже розглянули одне з таких, число Маха, поєднання швидкості і швидкості звуку. Чому число Маха - «унікальна» комбінація властивостей? Чи є інші, які так само важливі?

Існує досить простий спосіб ми можемо поглянути на те, як такі комбінації параметрів потоку рідини групуються разом, щоб впливати на сили та моменти на тіло в цьому потоці. У більш складних текстах це виявляється через процес, відомий як «мірний аналіз», і в книгах, де автор мав більше намірів продемонструвати свою математичну доблесть, ніж у навчанні розумінню фізичної реальності, процес використовує те, що називається «Теорема Бакінгем-Пі». Тут ми якраз задовольнимося описом найпростішого процесу.

Якщо ми подивимось на властивості рідини та інших місць, які викликають сили на тіло, як літак у польоті, ми можемо легко назвати кілька речей, таких як щільність, тиск, розмір тіла, гравітація, «липкість» або «в'язкість» рідини тощо. Як виявляється, ми могли б досить легко сказати, що більшість сил на літаку або ракеті в польоті певним чином функції наступних речей:

$F = F (ρ, V, л, μ, Р, г, а)$

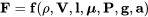
де,

ρ = щільність

V = швидкість

l = представницька довжина або розмір тіла

μ = в'язкість

Р = тиск

g = гравітація (вага)

a = швидкість звуку

В'язкість слід враховувати, щоб враховувати тертя між потоком і тілом, а швидкість звуку включена, тому що десь ми чули, що є такі речі, як велике опір збільшується зі швидкістю поблизу швидкості звуку.

Ми дійсно не знаємо на даний момент, наскільки загальним бути в розгляді цих термінів. Наприклад, ми вже знаємо з рівняння Бернуллі, що важлива швидкість у квадраті, а не просто швидкість, принаймні в деяких випадках. І ми могли б очікувати, що замість довжини це довжина в квадраті (площа), яка важлива у виробництві сил, оскільки ми знаємо, що сили надходять від тиску, що діє на область. Отже, давайте будемо повністю загальними і скажемо наступне:

$F = F (ρ А, ВБ, ЛК, мкД, Ге, ПГ, Аг)$

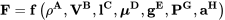
Наш простий аналіз не прагне знайти точні зв'язки або числа, а лише правильні функціональні залежності або комбінацію параметрів. Аналіз насправді просто питання балансування одиниць з двох сторін рівняння. Ліворуч у нас є одиниці сили (фунти або ньютони), де ми знаємо, що один фунт дорівнює одному слимаку раз один фут/сек. ² або що один Ньютон - кілограм-метр в секунду ². Таким чином, комбінація всіх одиниць, властивих всім термінам на правій стороні рівняння, також повинна вийти в цих точно таких же одиничних комбінаціях, як знайдено на лівій стороні рівняння. Іншими словами, коли всі одиниці враховуються на правій стороні рівняння, вони повинні поєднуватися, щоб мати одиниці сили;

(сл) ¹ (фут) ¹ (сек) ^-2 або (маса) ¹ (довжина) ¹ (час) ^-2.

Отже, у цій грі розмірного аналізу процедура полягає в заміні кожного фізичного члена з обох сторін рівняння на власні одиниці. Тоді ми можемо просто скласти всі експоненти з обох сторін і написати рівняння, що стосуються одиниці потужності. Наприклад, зліва у нас є одиниці маси (слимаки або кг) до першої потужності. Праворуч є кілька термінів, які також мають одиниці маси в них, і їх експоненти повинні складатися, щоб відповідати тій, що зліва.

сл ¹ = (сл ^А) (сл ^Д) (сл ^Г)

або оскільки експоненти додають:

1 = А + Д + Г

Ми можемо зробити ту ж математику для інших одиниць довжини та часу та отримати ще два співвідношення між показниками:

1 = -3А + Б + С — Д + Е — Г + Ч

-2 = -Б — Д — 2Е — 2Г — Ч

Ці три рівняння одиничних показників потім можуть бути вирішені через три з «невідомих», A, B і C.

А = 1 — Д — Г

Б = 2 — Д — 2Е — 2Г — Ч

С = 2 — Д + Е

Отже, де ми мали щільність до потужності А, або одиниць (sl/ft ³) ^A, ми тепер маємо:

(сл/фут ³) ^А = (сл) (сл) ^-D (сл) ^-Г (фут) ^-3 (фут) ^3D (фут) ^3G.

Ми робимо це з кожним терміном праворуч від функціонального співвідношення, а потім переставляємо терміни, групуючи всі терміни з однаковою буквеною експонентою і розглядаючи отримані групи. Ми отримаємо:

$F = F [(ρV2Площа) (ρVдовжина/μ) −D (довжина/v2) E (P/ρv2) G (V/A) −H]$

Отже, про що це нам говорить? Це говорить нам про те, що саме групування параметрів потоку та тіла праворуч важливі замість окремих параметрів у визначенні того, як тіло поводиться в потоці. Давайте розберемо кожен з них.

Перший термін праворуч є єдиним, який не має невизначеного показника. Рівняння по суті говорить, що однією з фізичних величин, яка впливає на вироблення сил на тіло в рідині, є це поєднання щільності, швидкості в квадраті та деякої площі (довжина в квадраті).

Якщо сила є функцією цієї комбінації термінів, це так само легко функція цієї групи, розділена на два; тобто

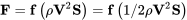
$F = F (ρv2s) = ф (1/2ρv2s)$

Зверніть увагу, що ми використовували букву «S» для області. Це може здатися дивним вибором, оскільки в інших галузях прийнято використовувати S для відстані; однак, в аеродинаміці прийнято використовувати S для «представницької області». Дійсно використовувана площа - це, як випливає з її назви, один представник аеродинаміки кузова. На літаку домінуючою областю для підйому та перетягування є крило, а S стає «плоскою областю» крила. На ракеті лобова область зазвичай використовується для S, як це стосується автомобілів та багатьох інших об'єктів.

Друге, що ми відзначаємо, це те, що термін праворуч зараз динамічний тиск разів на представницьку область. Тож ми переконалися, що динамічний тиск дійсно дуже важливий для впливу на продуктивність транспортного засобу в рідині.

Якщо ми подивимося на цю угруповання термінів:

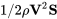
$1/2 ρV2S$

відзначимо, що він має одиниці сили (тиск разів на площу). Це означає, що всі одиниці на правій стороні нашого рівняння знаходяться в цьому одному члені. Інші комбінації параметрів в правій частині нашого рівняння повинні бути безодиничними. Це відразу очевидно в одному випадку, V/a, де і чисельник, і знаменник є швидкостями, і це можна перевірити у всіх інших, дивлячись на їх одиниці. Ми повинні визнати V/a як число Маха!

Тепер перепишемо рівняння:

$F/ [1/2ρV2s] = f [(ρVдовжина/μ) −D (довжина/v2) E (P/ρv2) G (V/A) −H]$

Це говорить про те, що безодиничне поєднання термінів зліва - це якось функція чотирьох комбінацій термінів праворуч. Що це за терміни і яку роль вони відіграють у виробництві сил на організм в рідині?

1.12 Коефіцієнти сили

Спочатку давайте подивимося на термін зліва. Цей неодиничний термін говорить нам про правильний спосіб «нерозмірності» сили рідини. Замість того, щоб говорити про ліфт, ми будемо говорити про безодиничний коефіцієнт підйому, C _L:

$КЛ = Л/ [1/2ρV2S]$

Ми також поговоримо про немірному коефіцієнті опору, C _D:

$CD = Д/ [1/2ρv2s]$

Ми використовуємо ці безодиничні «коефіцієнти» замість самих сил з двох причин. По-перше, вони приємні, тому що вони безроздільні, і нам не потрібно турбуватися про те, в якій системі ми працюємо. Якщо крило має коефіцієнт підйому, скажімо, 1,5, він буде дорівнює 1,5 або в англійській системі, або в SI, або в будь-якій іншій системі. По-друге, наш аналіз одиниць, цей бізнес «мірного аналізу», сказав нам, що більш доцільно для розуміння того, що відбувається з тілом у потоці, щоб подивитися на коефіцієнт підйому та коефіцієнт опору, ніж дивитися просто на підйомник і перетягування.

1.13 «Параметри подібності»

Тепер, як щодо умов праворуч? Наш аналіз говорить нам, що ці групування параметрів відіграють важливу роль у способі вироблення коефіцієнтів сили в рідині. Давайте розглянемо спочатку найпростіший, V/a.

V/a, на даний момент, повинен бути звичним для нас терміном. Це відношення швидкості тіла в рідині до швидкості звуку в рідині і називається воно числом Маха.

М = В/а.

Якщо ми летимо зі швидкістю звуку, ми знаходимося на «Mach One», де V = a, але що таке магія в Маху 1? У цьому має бути щось важливе, тому що ще в середині минулого століття аеродинаміки робили велику справу про порушення звукового бар'єру; тобто, йти швидше, ніж Мах 1. Щоб побачити, що суєта була і продовжує бути все про давайте подивимося на те, що відбувається на крилі, коли воно наближається до швидкості звуку.

Коли повітря рухається над крилом, воно розганяється до швидкості вище, ніж швидкість «вільного потоку». Іншими словами, при швидкості, дещо меншій, ніж швидкість звуку, швидкість зверху крила, можливо, досягала швидкостей, більших за швидкість звуку. Таке розгін до надзвукової швидкості не викликає ніяких проблем. Це уповільнення потоку знову, що проблематично. Надзвуковий потік не любить сповільнюватися і часто при цьому робить це зовсім раптово, через «ударну хвилю». Ударна хвиля - це раптове уповільнення потоку від надзвукової до дозвукової швидкості з супутнім підвищенням тиску (згадайте рівняння Бернуллі). Ця різка зміна тиску може легко спричинити відрив або відокремлення потоку над крилом, що призводить до великого пробудження за крилом та супутнього високого опору.

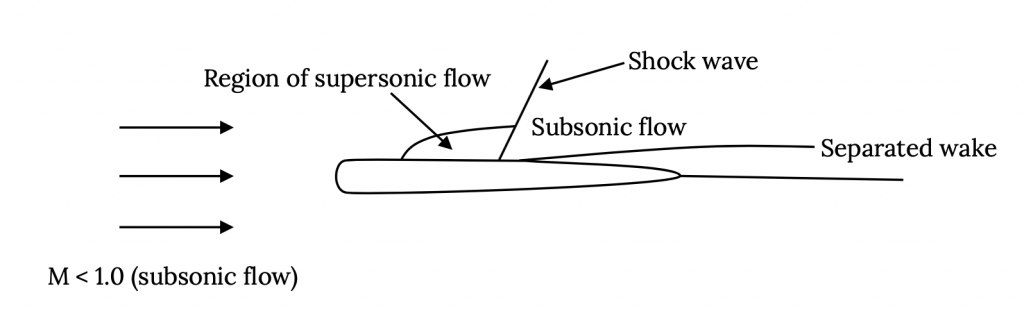
Оскільки дозвуковий потік, з числом Маха менше 1, наближається до аеропрофілю горизонтально, еліптична область надзвукового потоку утворюється на верхній поверхні перед зупинкою під кутовою ударною хвилею приблизно на півдорозі вниз по верхній поверхні аеропрофілю. Потік за межами ударної хвилі є дозвуковим, і починає відокремлюватися від аеропрофілю, утворюючи відокремлений прокид, який росте, коли він рухається далі вниз по аерофользі і повз заднього краю. — Малюнок 1.10: Формування ударної хвилі в «трансонічному» потоці

Таким чином, при деякій високій, але дозвукової швидкості (число Маха) надзвуковий потік над крилом розвинувся в тій мірі, в якій утворюється шок, і опір збільшується через відокремлене пробудження і втрати через шок. Точка, де це починає відбуватися, називається критичним числом Маха, M _crit . M _crit буде різним для кожного аерокрила та форми крила. Результатом всього цього є поведінка коефіцієнта опору щось на зразок того, що показано на графіку нижче:

Сюжет показує коефіцієнт опору ковпачок C sub cap D як функція числа Маха cap M. Cap C sub cap D є відносно постійним до досягнення критичного числа Маха, кришка M sub crit. Після ковпачка M sub crit, Cap C sub cap D зростає експоненціально перед вирівнюванням при ковпачку M рівному 1. Потім він трохи падає, утворюючи форму півкола навколо ковпачка M рівну 1, перед вирівнюванням і починає повільно збільшуватися, оскільки ковпачок М ще більше збільшується. — Малюнок 1.11: Збільшення коефіцієнта опору поблизу Mach One

Насправді теорія дозвукового стисливого потоку говорить про те, що підйом опору, який починається з критичного числа Маха, піднімається асимптотично на Маху 1; отже, міф про «звуковий бар'єр». На жаль, багато людей, особливо теоретики, здавалося, вважали, що реальність повинна відповідати їх теорії, а не навпаки, і думали, що коефіцієнт опору насправді став нескінченним на Маху 1. Вони мали свої переконання посилені, коли деякі високопотужні винищувачі у Другій світовій війні мали структурні та інші збої, коли вони наближалися до швидкості звуку в зануреннях. Коли ударна хвиля викликала поділ потоку, вона змінила спосіб підйому та опору вироблялися крилом, іноді призводячи до структурного руйнування на крилах та хвостових поверхнях, які не були призначені для цих розподілів сил. Це поділ потоку також може зробити контрольні поверхні на хвості та крилах марними або навіть призвести до їх «зворотного» ефективності. Пілот залишився з літаком, який, якщо він залишався разом конструктивно, часто ставало неможливим для управління, що призвело до аварії. Іноді, якщо літак тримається разом, і пілот міг зберегти свідомість, число Маха літака зменшиться достатньо, оскільки він досяг меншої висоти (швидкість звуку є функцією температури і вище на меншій висоті), і проблема зникне, дозволяючи пілоту жити, щоб сказати розповідь.

У будь-якому випадку, експериментатори прийшли на допомогу, зазначивши, що кулі протягом багатьох років пішли швидше, ніж швидкість звуку («ви ніколи не почуєте постріл, який вбиває вас») і спроектувавши літак у формі кулі, Bell X-1, з достатньою тягою, щоб отримати його до і повз Маха 1.

Дзвін мав прямі крила, які звужуються, коли вони вийшли з фюзеляжу літака. Сам фюзеляж підійшов до точки в носі, з витягнутим стрижнем, прикріпленим до самого носа. Потім фюзеляж підтримував циліндричну форму перед звуженням, коли він наближався до вихідного отвору двигуна, з вертикальними та горизонтальними хвостами, встановленими трохи вище виходу двигуна. — Малюнок 1.12: Дзвін X-1

Після того, як літак насправді надзвуковий, насправді є два поштовхи на крилі, один на передньому краї, де потік раптово сповільнюється від надзвукової швидкості вільного потоку до дозвукової, коли він досягає точки застою, і один ззаду, де надзвуковий потік над крилом знову сповільнюється. В результаті «звуковий бум» чути з літака на надзвукових швидкостях дійсно дві послідовні стріли замість одного удару.

Тому важливо, щоб ми були в курсі числа Маха потоку, тому що сили, такі як перетягування, можуть різко змінюватися, коли число Маха змінюється. Ми, звичайно, не хочемо намагатися передбачити сили на надзвуковому літаку за результатами випробувань на дозвукових швидкостях або навпаки. З іншого боку, поки все, що ми розглядаємо, відбувається нижче критичного числа Маха, нам може не потрібно турбуватися про ці «ефекти стисливості». Загалом, нижче M _crit можна вважати потік «нестисливим» і припустити, що щільність є постійною. Вище M _crit ми не можемо цього зробити, і ми повинні використовувати стислу форму рівнянь, як рівняння Бернуллі.

Виходячи з вищесказаного, одне ім'я, яке ми часто даємо числу Маха, є «параметром подібності». Параметри подібності - це речі, які ми повинні перевірити, переконавшись, що наші експериментальні вимірювання та розрахунки належним чином враховують такі речі, як підйом опору, який починається з M _crit. Ми не хочемо намагатися передбачити ефекти стисливого потоку, використовуючи нестисливі рівняння або результати випробувань або навпаки.

Інші три терміни в нашому силовому відношенні також є параметрами подібності. Давайте подивимося на перший термін з правого боку цих відносин. Ця угруповання термінів відома як число Рейнольдса. Число Рейнольдса можна побачити в різних текстах, скорочених по-різному [Re, Rn, R, Re _x тощо] залежно від конвенції в галузі використання та від її застосування. Тут ми будемо використовувати Re.

$Re= [ρVI] /μ$

Число Рейнольдса - це дійсно співвідношення сил інерції та в'язких сил у рідині і є дуже реальним чином мірою здатності потоку слідувати за поверхнею, не відокремлюючи.

Число Рейнольдса також є показником поведінки потоку в тонкій області поруч з тілом у потоці, де домінують в'язкі сили, визначаючи, чи добре поводиться цей потік (ламінарний) або випадково брудний (турбулентний). Ця тонка область називається прикордонним шаром.

Інерційні сили - це ті сили, які змушують тіло або молекулу в потоці продовжувати рухатися з постійною швидкістю і напрямком. В'язкі сили є результатом зіткнень між молекулами в потоці, які змушують потік, принаймні в мікроскопічному масштабі, змінювати напрямок. Поєднання цих сил, як відображено в Числі Рейнольдса, може призвести потік, щоб бути гладким і впорядкованим і легко відірватися від поверхні або бути випадковим і турбулентним і, швидше за все, слідувати кривизні тіла. Вони також регулюють величину тертя або в'язкого опору між тілом і потоком.

Загалом, ламінарний прикордонний шар, який виникає при нижчих числах Рейнольдса, призводить до низького опору тертя (тертя шкіри), але не дуже добре протистоїть поділу і може сприяти великому «пробудженню» . Турбулентний прикордонний шар, який виникає при вищих числах Рейнольдса, має більш високий опір тертя, але чинить опір поділу потоку краще, що призводить до зниження «пробудження» опору. Так чого ми хочемо? Це все залежить від форми тіла і відносних величин неспання і опору тертя.

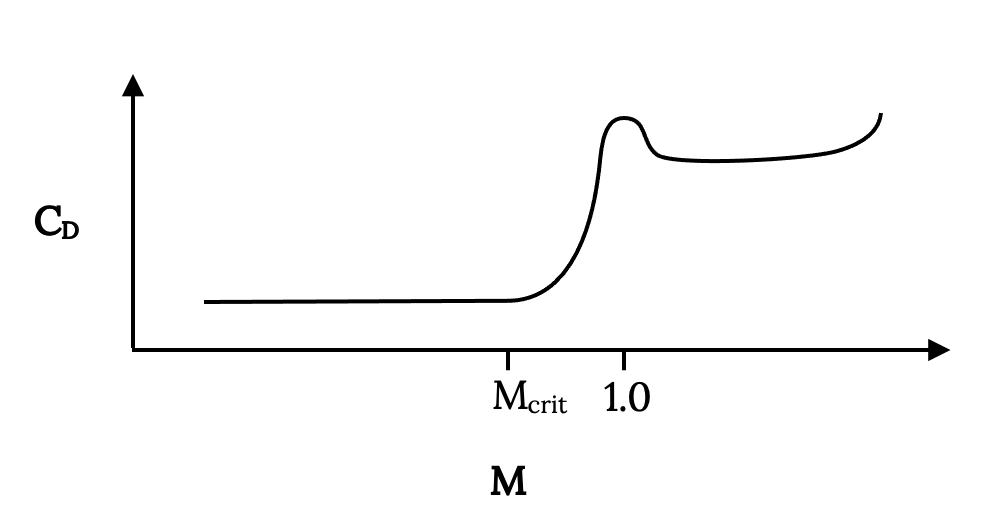
Класичним випадком для вивчення є потік навколо кругового циліндра або, у трьох вимірах, над сферою.

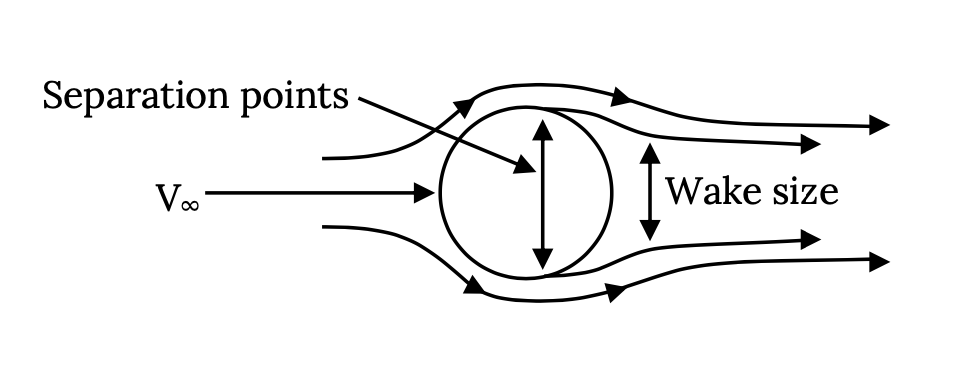
Потік наближається до циліндра з ковпачком V sub нескінченності. Потік змушує рухатися навколо циліндра, відокремлюючись від поверхні циліндра в точках поділу з кожного боку безпосередньо за найширшою точкою кліндера. Поділ трохи стискається, коли він віддаляється від циліндра, при цьому відстань між відокремленими обтіками позначається як розмір пробудження. — Малюнок 1.13: Обтікання кругового циліндра

Потік над круглим циліндром або сферою, як правило, слідує за його поверхнею приблизно на півдорозі навколо тіла, а потім відривається або відокремлюється, залишаючи «прокидання» «мертвого» повітря. Це пробудження викликає велику тягу. Ця хвиля схожа на те, що спостерігається при їзді під дощем за автомобілями і особливо великими вантажівками. На вантажівці точка, де потік розділяється, знаходиться приблизно в задніх кутах кузова причепа або задньої двері. На автомобілі це часто менш чітко визначено з поділом, що відбувається десь між верхньою частиною заднього скла та задньою частиною транспортного засобу. На аеродинамічно добре спроектованому автомобілі точка поділу буде прямо в куті задньої палуби або на «спойлері», якщо автомобіль має такий. Маленьке пробудження дає менший опір, ніж великий поминки.

На круговому циліндрі або сфері точка поділу значною мірою залежатиме від числа Рейнольдса потоку. При більш низьких значеннях Re потік поруч з поверхнею тіла в «прикордонному шарі» має тенденцію бути «ламінарним», потік, який не дуже добре протистоїть відриву від поверхні або відокремлення. Нижня Re зазвичай призводить до відокремлення дещо до того, як потік досягне точки півдорозі (90 градусів) навколо форми, що дає великий прокидання та високий «опір пробудження». При вищому Re потік у прикордонному шарі має тенденцію бути турбулентним і здатний протистояти поділу, що призводить до поділу в якийсь момент за межі точки півдорозі та меншого перетягування пробудження та пробудження.

Оскільки опір пробудження є переважною формою опору на формі, як сфера або круговий циліндр, набагато більша за величиною, ніж опір тертя, точка поділу потоку є домінуючим фактором у визначенні значення коефіцієнта опору тіла.

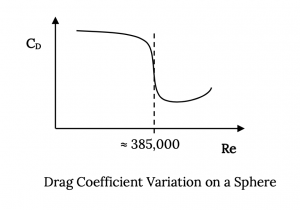
Коефіцієнт опору ковпачок C sub cap D показаний як функція числа Рейнольдса, ковпачок R e Cap C sub cap D повільно зменшується у міру збільшення числа Рейнольдса, але зменшується асимптотично, коли число Рейнольдса наближається до 385 тис. Cap C sub cap D потім продовжує зменшуватися після проходження 385 тисяч, але рівні незабаром після цього і починає збільшуватися, оскільки число Рейнольдса ще більше збільшується. — Малюнок 1.14: Варіація коефіцієнта опору з числом Рейнольдса для сфери

У наведеному вище графіку число Рейнольдса базується на діаметрі сфери, а коефіцієнт опору падає від значення приблизно 1.2 до приблизно 0,3, оскільки «критичне» число Рейнольдса передається при значенні близько 385,000. Це величезне зниження коефіцієнта опору і ілюструє, наскільки потужний вплив Re може мати на потік і результуючі сили на тіло.

Зверніть увагу, що потік навколо циліндра або сфери може впасти в частині високого опору вищевказаної кривої через кілька речей, оскільки Re залежить від щільності, швидкості, репрезентативної довжини та в'язкості. Щільність і в'язкість - це властивості атмосфери, які в тропосфері зменшуються з висотою. Основними речами, що впливають на Re та поведінку потоку на будь-якій заданій висоті, будуть швидкість потоку та «характерна довжина» або розмір тіла. Низька швидкість потоку та/або невеликий розмір призведе до низького Re і, отже, до високого коефіцієнта опору. Маленький провід (круглий циліндр) матиме набагато більший коефіцієнт опору, ніж великий циліндр при заданій швидкості.

Звичайно, коефіцієнт опору не є перетягуванням. Перетягування також залежить від проектованої площі тіла, щільності повітря і квадрата швидкості:

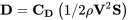
$Д = КД (1/2ρV2s)$

Отже, загалом не можна констатувати, що мала сфера матиме більше опору, ніж велика, оскільки перетягування залежатиме від швидкості в квадраті та площі, а також від значення коефіцієнта опору. З іншого боку, багато поширених об'єктів сферичної форми кидають виклик нашій інтуїції у своїй поведінці перетягування через це явище. Куля для боулінгу, розміщена в аеродинамічній трубі, буде демонструвати виражене зменшення опору, оскільки швидкість тунелю збільшується, а число Рейнольдса близько 385,000 передається. Сфера розміром м'яч для гольфу або бейсбол буде на суб-критичного числа Рейнольдса навіть на швидкості набагато більше 100 миль/год. Це причина, ми покриваємо м'ячі для гольфу з «ямочками» і бейсбольні глечики, як потерти бейсбольні м'ячі, перш ніж кидати їх. Наявність шорсткої поверхні може зробити потік прикордонного шару турбулентним навіть при числах Рейнольдса, де потік зазвичай буде ламінарним.

Поведінка C _D, показана на графіку вище, призначена для гладкої сфери або кругового циліндра. Та ж форма з шорсткою поверхнею зазнає «переходу» від поведінки високого коефіцієнта опору до нижчих значень C _D при значно нижчих числах Рейнольдса. Шорстка поверхня створює власну турбулентність у прикордонному шарі, яка впливає на поділ потоку приблизно так само, як і «природна» турбулентність, що виникає внаслідок сил у потоці, що визначають значення Re. Ранні гравці в гольф, граючи з гладкою м'ячі для гольфу, ймовірно, з'ясував, що, як тільки їх м'яч мав кілька потертостей або порізів, Він насправді поїхав далі. Вони, ймовірно, тоді почали експериментувати з візерунками пазів, вирізаними на поверхні кульок. Це призвело до ямочки візерунки ми бачимо сьогодні, які ефективно знизити опір м'яч для гольфу (це не все добре, так як ті ж ямочки зробити гольфіст 's гачок або скибочку гірше). Шви на бейсбол мають той же ефект, і бейсбольні глечики знайшли у своїх власних дещо ненаукові експерименти, що подальше натирання обкладинки нового м'яча може змусити його йти швидше так само, як плювання на нього може змусити його робити інші дивні речі.

Сфера або циліндр, як уже згадувалося раніше, є класичною формою, де є великі ефекти Re на перетягування. Інші форми, особливо «обтічні» або низькі форми перетягування, такі як аерозолі та крила, не будуть демонструвати таких драматичних залежностей від перетягування Re, але ефект все ще існує і його потрібно враховувати.

Як і число Маха, Re вважається параметром «подібність», тобто ми хочемо знати, що відбувається з такими речами, як коефіцієнт підйому та опору на тілі, ми повинні знати його число Рейнольдса і знати, на якій стороні будь-якого «критичного Re» ми можемо бути на. Потік над крилом може бути досить різним при докритичних значеннях Re, ніж при більш високих значеннях, насамперед з точки зору місця поділу потоку, затримки, а також за величиною опору тертя, що залежить від ступеня ламінарного та турбулентного потоку на поверхні крила.

Отже, виконуючи розрахунки та випробування аеродинамічної труби, ми повинні дивитися на величину Re та її наслідки. При цьому ми можемо потрапити в деякі реальні труднощі, коли ми тестуємо масштабні моделі в аеродинамічній трубі. Якщо ми, наприклад, протестуємо одну десяту масштабну модель літака в аеродинамічній трубі, наш «характерний вимір» в числі Рейнольдса буде 1/10 від повної шкали. Отже, якщо ми хочемо, щоб зіставити тест Re з повною площиною масштабу, один з інших термінів повинен бути змінений в десять разів. Зміна швидкості на порядок до десяти разів повної швидкості масштабу, очевидно, змусить нас зіткнутися з іншим параметром подібності, числом Маха, так що це не принесе користі. Ми повинні змінити щось інше або «обдурити», використовуючи штучну шорсткість, щоб створити турбулентний прикордонний шар, коли значення числа Рейнольдса дійсно занадто низьке для турбулентного прикордонного шару.

Один з найбільших проривів у повітроплаванні стався в 1920-х роках, коли Національний консультативний комітет з аеронавтики (NACA) на Ленглі Філд, VA побудував те, що вони назвали «аеродинамічною трубою змінної щільності». Це був випробувальний комплекс, де щільність повітря може бути збільшена в 20 разів, що дозволило випробувати моделі масштабу 1/20 в повному масштабі Reynolds Numbers. VDWT, нині Національний історичний пам'ятник, був дозвуковою аеродинамічною трубою, побудованою всередині яйцеподібної сталевої оболонки під тиском. Досить складний для свого часу тунель був під тиском до 20 атмосфер після установки моделі крила. Тунель експлуатувався, і тестова модель була переміщена через діапазон випробувальних кутів атаки операторами, які спостерігали за своїми випробуваннями через герметичні вікна, що нагадували корабельні ілюмінатори. Крила моделі, кожне з п'ятидюймовим акордом і тридцятидюймовим прольотом, були оброблені з дуже жорсткими допусками на основі розмірів, розроблених вченими та інженерами NACA. Вперше світ повітроплавання мав надійні, повномасштабні аеродинамічні вимірювання крил з широким діапазоном форм аеронавтики.

Сьогодні в аеродинамічній трубі тестування ми зазвичай «обманюємо» на номер Рейнольдса, використовуючи «смуги поїздки», невеликий наждачний папір, як лінії, розміщені біля передніх країв крил і фюзеляжів, щоб змусити потік переходити від ламінарного до турбулентного потоку в місцях, розрахованих до випробувань. Хоча аеродинамічна труба змінної щільності була давно звільнена, ми все ще маємо унікальну здатність на тому, що зараз є родовищем НАСА-Ленглі з Національним трансзвуковим об'єктом, аеродинамічною трубою, в якій робочим газом є азот при температурах дуже близько його точки ліквідації. Оскільки щільність, в'язкість і швидкість звуку змінюються з температурою, в NTF можна одночасно імітувати повномасштабні числа Рейнольдса та Маха. Хоча тестування не є простим при цих низьких температурах, належним чином запускати дослідження в NTF можуть дати аеродинамічні дані, які не можуть бути отримані іншим способом.

Завершуючи це обговорення числа Рейнольдса, слід зазначити, що «характерна довжина» в Re може приймати кілька різних значень залежно від умовності, і що значення Re, при якому відбувається перехід від ламінарного до турбулентного потоку, також може змінюватися залежно від застосування. Як показано раніше, ми базуємо число Рейнольдса для круглого циліндра або сфери на його діаметрі. Перехід Re трохи менше 400 000. Однак, якби ми були механічними або будівельними інженерами, які працюють з потоками по трубах, ми б використовували діаметр труби як наш розмір, і ми виявили б, що перехід відбувається при Re близько 5000, приблизно на два порядки відрізняються від переходу на сферу. Ми повинні усвідомлювати цей інший погляд на важливі величини Re, коли розмовляємо з нашими друзями в інших сферах про потоки.

Коли ми говоримо про значення числа Рейнольдса на крилі або літаку, характерним виміром використовується середня або середня хорда крила, середня відстань від ведучого крила до заднього краю. Коли ми робимо детальні розрахунки щодо поведінки потоку в прикордонному шарі, ми будемо використовувати ще один вимір, відстань від точки застою над поверхнею тіла до точки, де ми робимо розрахунки.

Добре, ми знайшли наше щось про важливість числа Маха і числа Рейнольдса, як щодо інших двох груп параметрів у рівнянні залежності сили ми мали раніше?

Існували ще два терміни, gl/v ², і P /ρ V. Перший з них - це співвідношення гравітаційних та інерційних сил і стосується сил, які виникають внаслідок того, що тіло знаходиться близько до «інтерфейсу», такого як земля або поверхня океану. Цей термін зазвичай перевернутий, а його квадратний корінь відомий як число Фруда.

Число Фрунда = V/[gl] ^1/2,

де довжина в рівнянні - відстань між тілом і інтерфейсом рідини; тобто висота літака над злітно-посадковою смугою або глибина підводного човна під поверхнею. Якщо ця відстань не менше приблизно в два рази більше діаметра підводного човна або хорди крила, номер Фруда, як правило, можна ігнорувати; але в цьому діапазоні це може допомогти врахувати збільшення опору або підйому, які можуть виникнути, коли тіло знаходиться поблизу поверхні.

Останній термін, число Ейлера, P/ρ V, насправді не важливий у повітрі, але використовується при пошуку ймовірності кавітаційних ефектів на тіло у воді. Коли тиск у воді знижується до точки пари води при заданій температурі, вода закипить, навіть якщо температура нижче звичайної температури кипіння. Коли потік прискорюється навколо гвинта або корпусу судна тиск може стати досить низьким локально, щоб кип'ятити воду, і це кипіння або кавітація може спричинити серйозне збільшення опору, шуму, втрати тяги гвинта та пошкодження самої поверхні. Термін, який використовується для вивчення цього, є модифікацією тієї, яка знайдена в нашому аналізі, трохи переписана, щоб врахувати важливість тиску пари.

$Кількість кавітації (σ) = [P−Pv] /ρv2$

Відзначимо, що знаменник - це звична угруповання параметрів, в два рази перевищує динамічний тиск.

1.14 Аеродинамічні коефіцієнти та їх аеродинамічні коефіцієнти

На початку цього тексту ми розглянули термінологію, яка використовується для визначення форми аеропрофілю, такі речі, як акорд, розвал і товщина, а також такі речі, як проліт, акорд, розгортка та співвідношення сторін, які визначають форму повного крила. У розділі вище ми виявили, що найкращий спосіб говорити про сили, що діють на аерофользі (2-D) або крило (3-D), - це з точки зору нерозмірних коефіцієнтів. Давайте ще раз поглянемо на ці коефіцієнти та те, як вони визначаються як у двох, так і в трьох вимірах, і подивимося на те, як вони змінюються як функція крила або кута атаки на потік.

Кілька сторінок назад ми визначили коефіцієнти підйому і перетягування для крила. Вони повторюються нижче і розширюються для визначення коефіцієнта моменту качки:

$CL=L/ [1/2ρV2s] = Коефіцієнт підйому$

$CD=D/ [1/2ρv2s] = коефіцієнт опору$

$СМ = М/ [1/2ρV2Sc] = Коефіцієнт моменту$

Зауважте ще раз, що область «S» - це площа «planform» крила, «проектовану» область, яку можна побачити, дивлячись вниз на крило, а не на фактичну площу поверхні. Коефіцієнт моменту має дещо інший знаменник, який включає середню або середню хорду разом з плоскою площею для того, щоб зробити коефіцієнт безодиничним, оскільки момент качки має одиниці сили часу відстані. Трохи пізніше ми розглянемо даний момент більш детально і подивимося, яку опорну точку (точки) слід використовувати при вимірюванні або обчисленні цього моменту.

Наведені вище коефіцієнти мають тривимірну форму і такі, як ми б їх визначили для повного крила. Якщо ми просто дивимося на ділянку аеропрофілю, двовимірний зріз крила, площа в знаменнику просто стала б хордою.

$CL=L/ [1/2ρV2C] = 2-D коефіцієнт підйому$

$CD=D/ [1/2ρv2c] = 2-D коефіцієнт опору$

$СМ = М/ [1/2ρV2C2] = коефіцієнт 2-D моменту$

Було б корисно знати щось про типові діапазони цих коефіцієнтів у двох або трьох вимірах, тому ми матимемо деяке уявлення про те, наскільки дійсними можуть бути наші розрахунки.

-2.0 < C _L < +2,0 для звичайного крила або аерокрила без закрилків

-3 .0 < C _L < +3 .0 для крила або аерокрила з заслінками

0,005 < C _D < 0,025 для крила або аерокрила (більше для цілого літака)

-0.1 < C _M < 0.0 для крила або аерокрила при вимірюванні c/4

Слід також зазначити, що момент качки визначається як позитивний, коли він «ніс вгору». Залежно від напрямку аерокрила або крила всередині системи осі це може суперечити математичному звичаю. Насправді, більшість текстів зазвичай розглядають проблеми аеродинаміки так, ніби швидкість вільного потоку йде зліва в позитивному напрямку x, а крило або аеродинаміка звернені вліво в негативному напрямку x. У такому зображенні позитивний момент качки буде за годинниковою стрілкою, хоча звичайне математичне лікування присвоїло б цьому негативний знак.

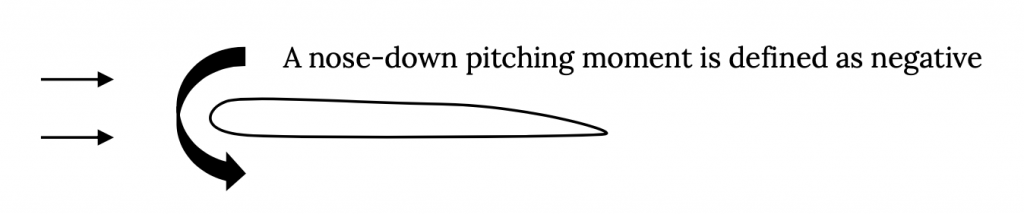
Коли горизонтальний потік повітря призведе до моменту проти годинникової стрілки, що піднімає передню кромку вниз, що визначається як негативний момент качки носом вниз. — Малюнок 1.15: Визначення знака качки моменту

1.15 Кут атаки

Нам також потрібно визначити спосіб співвіднесення орієнтації крила з потоком; i, е., кут атаки крила або аерокрила, α. При цьому ми можемо подивитися на визначення напрямку підйому і перетягування.

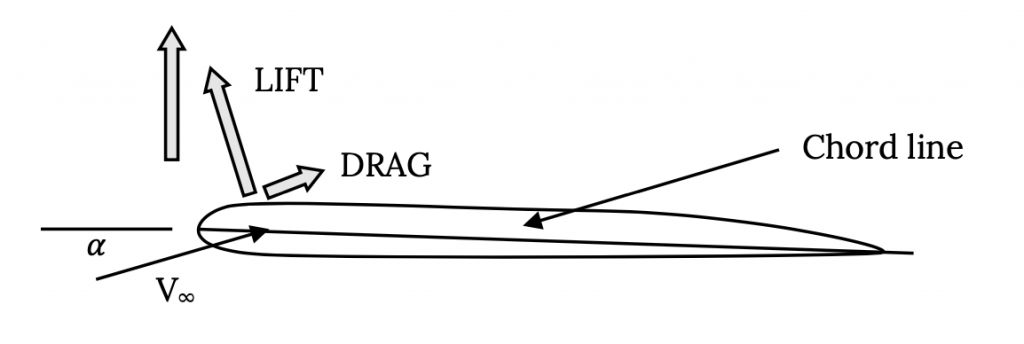
Коли повітря, що протікає з ковпачком швидкості V sub нескінченності, наближається до аеропрофілю з кута альфа нижче лінії хорди, від підсумовування вектора Lift, нормаль до напрямку повітряного потоку, а вектор перетягування вирівнюється з напрямком повітряного потоку. — Рисунок 1.16: Взаємозв'язок між підйомом, перетягуванням та швидкістю вільного потоку

Зверніть увагу, що кут атаки, α, визначається як кут між хордою крила або аерофольга і вектором швидкості вільного потоку, а не між швидкістю і горизонталлю. Також зверніть увагу, що Lift and Drag визначаються як перпендикулярно і паралельно відповідно вектору швидкості вільного потоку, а не «вгору і назад» або перпендикулярно і паралельно хорді. Ці визначення часто вимагають обережності, оскільки вони не завжди інтуїтивно зрозумілі. У багатьох ситуаціях сила, яку ми визначаємо як підйом, матиме «вперед» компонент до нього вздовж лінії хорди крила. Це, по суті, причина того, що лопаті ротора вертольота та гірокоптера можуть обертатися без потужності в тому, що відоме як режим «автообертання», даючи підйом з непрацюючим ротором.

З огляду на ці визначення, давайте подивимося, як коефіцієнт підйому і опору зазвичай змінюються з кутом атаки.

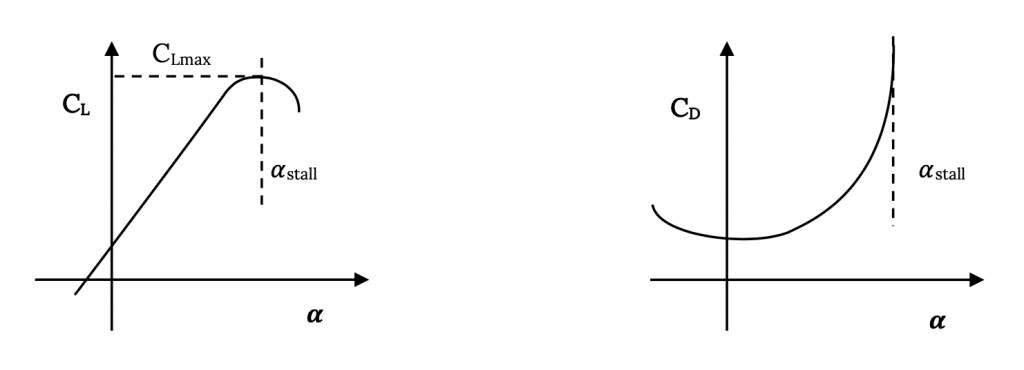
а) Коефіцієнт підйому cap C sub cap L показаний як функція кута атаки, альфа. Cap C sub cap L є лінійним, поки він не наближається до альфа-суб стійла, де його нахил зменшується до досягнення пікової кришки C sub cap L max на альфа-суб стійло. Cap C sub cap L потім швидко зменшується. b) Коефіцієнт перетягування ковпачка C sub cap D відображається як функція кута атаки, альфа. Cap C sub cap D слідує за розширеною параболічною кривою, з її мінімальним майже альфа дорівнює 0, і зростає, оскільки він асимптотично наближається до альфа-суб стійла. — Малюнок 1.17: Ділянки коефіцієнта підйому та опору проти α, що показують стійло

Давайте розглянемо кілька речей в наведених вище сюжетах:

1. Коефіцієнт підйому змінюється лінійно з кутом атаки, поки крило не наближається до стійла. Стійло починається, коли потік починає відриватися або відокремлюватися від верхньої поверхні крила і може швидко або поступово прогресувати по поверхні.
2. Коли коефіцієнт підйому більше не збільшується з кутом атаки, в середині прогресії стійла, ми маємо C _Lmax найбільше значення коефіцієнта підйому, яке ми можемо отримати для конкретного аеродрому або крила при заданому числі Рейнольдса. Значення C _Lmax буде, в цілому, збільшуватися зі збільшенням Re.
3. Коефіцієнт підйому не відображається як нуль за значенням при нульовому куті атаки. На «симетричному» аеродромі; тобто на одному без розвалу, підйом буде дорівнює нулю під нульовим кутом атаки. На вигнутому аеродромі ліфт буде нульовим при деякому негативному куті атаки, який ми називаємо «нульовим кутом підйому атаки», α L0.
4. Перетягування швидко збільшується в стійлі.

Ми повинні вивчити цю ідею стійла далі, тому що тут щось здається неправильним. Наведений вище сюжет показує, що стійло - це те, де ми маємо максимальний коефіцієнт підйому. Як це може бути правдою, коли нам завжди говорили, що стійло - це де літак втрачає ліфт?

Наша дилема тут випливає зі значень двох різних термінів, коефіцієнта підйому та підйому. Давайте розглянемо взаємозв'язок між підйомним і підйомним коефіцієнтом.

Ліфт = CL [1/2 ρ V2S]

Щоб мати підйом, ми повинні мати дві речі, хороший коефіцієнт підйому та швидкість, необхідну для перетворення цього коефіцієнта підйому на підйом. Так в чому ж тут проблема? Проблема полягає в перетягуванні.

Коли літак досягає C _Lmax, він має найвищу можливу підйомну здатність або коефіцієнт підйому. Але дивлячись на інший сюжет, коефіцієнт опору, ми бачимо, що він також має швидко зростаючий коефіцієнт опору. Отриманий опір спричиняє зниження швидкості, і оскільки швидкість знаходиться в квадраті у співвідношенні вище, вона має набагато більш потужний вплив на підйом, ніж коефіцієнт підйому. Підйом зменшується, коли швидкість падає, і, дійсно, незважаючи на те, що у нас дуже високий коефіцієнт підйому, ми не можемо зробити достатньо підйому, щоб подолати вагу літака. І, як ми бачимо з сюжету зліва, якщо ми пройдемо повз стійла кута атаки, ми також отримаємо зниження коефіцієнта підйому.

Як зазначалося вище аж до зупинки, показано, що коефіцієнт підйому лінійно змінюється з кутом атаки і стає нульовим при нульовому куті підйому атаки _L0. З огляду на це, ми можемо написати просте рівняння для значення C _L.

$CL= (ДКл/Dα) [α−αL0]$

Теорія покаже, і експеримент перевірить, що для перерізу аерокрила (двомірний зріз крила) цей _{нахил, dC L/d} α , дорівнює 2 π, де кути атаки виражається в радіанах. Так теоретично для перерізу аеропрофілю це рівняння стає:

$Cl=2π [α−αL0]$

Для тривимірного крила нахил кривої може бути меншим, і як теорія, так і експеримент можуть бути використані для визначення цього 3-D нахилу.

Отже, як форма перерізу аеропрофілю впливає на цей зв'язок? По-перше, форма лінії розвалу визначить значення нульового кута підйому атаки. У більш пізньому курсі аеродинаміки ми знайдемо, що існують способи обчислити _L0 від форми лінії розвалу аеропрофілю.

Складніше і може бути навіть неможливо розрахувати значення C _Lmax і кут атаки для стійла. Це функції товщини аеропрофілю та форми його поверхні, а також таких речей, як число Рейнольдса. Ми повинні подивитися на ефекти тертя та теорію прикордонного шару, щоб навіть почати успішно боротися з областю стійла. Наша єдина альтернатива - використовувати тестування аеродинамічної труби. І це те, що люди з Національного консультативного комітету з аеронавтики (NACA), про який згадувалося раніше, зробили у своїй аеродинамічній трубі змінної щільності.

1.16 Аеродроми NACA

У 1920-х роках вчені та інженери NACA поставили перед собою намір вперше систематично вивчити, як такі речі, як форма лінії розвалу та розподіл товщини, впливали на поведінку аеродромів. Вони почали свої пошуки, вирішивши, як визначити форму аеропрофілю, використовуючи лише три цифри та чотири цифри. Вони подивилися на найкращі форми аеропрофілю свого часу і знайшли хороший спосіб змінити товщину аеропрофілю від його переднього краю до заднього краю і написали рівняння для цього розподілу, яке дозволило визначити все з точки зору одного, двозначного числа. Потім вони написали два рівняння для лінії розвалу аерокрила, одне для передньої частини крила до точки максимального розвалу, а інше для кормової частини крила за максимальним розташуванням розвалу. Ці два рівняння залежали від двох однозначних чисел, одне давало розташування максимальної точки розвалу в десятих частках хорди, а інше давало максимальну відстань між лініями розвалу і хорди в сотих частках хорди. Потім вони використовували ці чотири цифри для ідентифікації отриманого аерофольгу.

Наприклад, аеропрофіль NACA 2412 - це аеропрофіль, де кожне з чисел означає щось про форму:

2 - Максимальна відстань між лініями акорду та розвалу становить 2% від акорду.

4 - Розташування точки максимального розвалу знаходиться на 40% хорди.

12 — Максимальна товщина аерокрила становить 12% хорди.

Ці чотири цифри (три числа) потім можуть бути використані з відповідними рівняннями для малювання форми аеропрофілю.

Використовуючи цей метод, NACA міг систематично дивитися на ефекти тільки величини максимального розвалу, тестуючи ряд форм, таких як 1412, 2412, 3412 і т.д., або вони могли тримати максимальний розвал стійко і дивитися на ефект розміщення максимального розвалу (2212, 2312, 2412, 2512 і т.д.), або виправити форму лінії розвалу і подивіться на ефект зміни товщини (0006, 0009, 0012, 0015, 0021 і т.д.). Зверніть увагу, що цей останній набір аеропрофілів є симетричними; тобто нульовий розвал. І це саме те, що було зроблено з випробуваннями на сотнях аеродромів. У аеродинамічній трубі змінної щільності було протестовано широкий спектр аеродинамічних профілів та побудовані результати. Зразки сюжетів представлені в додатку А.

Перший набір, Цифри A-1 (A&B), призначений для секції аеропрофілю NACA 0012. Зверніть увагу, що це симетричний перетин аеропрофілю (перший нуль вказує на відсутність розвалу і при цьому друге число безглузде) і має 12% товщини. Спочатку ми бачимо, що на кожному з двох графіків є кілька графіків і що для кожної ділянки існує кілька визначень вертикальної осі. На графіку ліворуч горизонтальна вісь - це кут атаки, заданий у градусах, а первинна вертикальна вісь - секція або двовимірний коефіцієнт підйому. Існує також вторинна вертикальна вісь для коефіцієнта качінгового моменту (з моментом, виміряним щодо c/4, чверть хорди).

Існує багато інформації, наведеної на ділянці А. Перше, що ми відзначаємо, це те, що існує два набори кривих коефіцієнта підйому, і кожен з них, здається, має пару різних ділянок області стійла. Зверніть увагу, що лінійна частина однієї множини цих кривих проходить через вісь графіка, показуючи, що коефіцієнт підйому дорівнює нулю під кутом атаки нуль. Ці криві призначені для базового аеропрофілю 0012, який є симетричним аерофолистом і не матиме горища під нульовим кутом атаки.

Є, як зазначалося вище, принаймні дві різні ділянки області стійла для цього симетричного аеропрофілю. Щоб зрозуміти це, нам потрібно подивитися на інформацію про вставку числа Рейнольдса (на цих ділянках відзначається просто «R»). У цій вставці показано чотири різних символів. Символ «алмаз» позначав дані для крила, випробуваного при числі Рейнольдса 9 х 10 ⁶, квадрата для Re = 6 х 10 ⁶, а окружності для Re = 3 х 10 ⁶. Інший символ, трикутник, призначений для аеропрофілю, випробуваного з «стандартною шорсткістю» або шорсткою поверхнею при Re = 6 х 10 ⁶. Зазвичай, чим вище значення числа Рейнольдса, тим вище значення максимального коефіцієнта підйому, але в цьому конкретному випадку спостерігається лише незначне збільшення, коли C _Lmax рухається вгору приблизно від 1,5 до 1,6, оскільки число Рейнольдса на гладкому аеродромі збільшується від 3 до 6 х 10 ⁶. За гладкою поверхнею стійло завжди відбувається під кутом атаки 16 градусів. Відзначимо також, що аерофольг також глухне під кутом атаки мінус 16 градусів, перевіряючи його симетричну поведінку. Шорстка поверхня викликає набагато більш раннє затримання і більш низьке значення C _Lmax.

Отже, який інший набір «кривих підйому», які зміщені вгору і вліво на цій ділянці? Це дані для аеропрофілю 0012 з заднім краєм заслінки. Інша інформація про вставку на сюжеті говорить нам, що це розщеплений клапоть з акордом 20% аерофольги і він відхилений на 60 градусів. Зверніть увагу, що базовий аеродром малюється в масштабі на правій ділянці, а стулка і його прогин відзначаються пунктирними лініями на кресленні.

Ці дані показують, що для цієї конкретної заслінки крива підйому зсувається вліво таким чином, що вона має нульовий підйом при мінус 12 градусах, іншими словами α _LO, нульовий кут підйому атаки, становить мінус 12 градусів для закритого аерокрила. Криві показують, що відхилення заслінки збільшився C _Lmax приблизно з 1,6 до приблизно 2,4, збільшення на 50%. C _Lmax для шорсткої поверхні аеродрому пішов від 1,0 до 1,9.

Тепер на цій ділянці є дві інші криві. Вони є кривими для коефіцієнта качального моменту близько чверті хорди, з відхиленням щитка і без нього. Спочатку зауважте, що шкала зліва від ділянки відрізняється для коефіцієнта моменту, ніж для коефіцієнта підйому. Не варто плутати ці дві шкали. Далі зверніть увагу, що верхня з цих двох кривих призначена для крила без закрилків і що вона має значення нуля в діапазоні кута атаки, де крива підйому лінійна. Це означає, що момент пітчингу дорівнює нулю на чверті хорди для цього аеропрофілю. Це справедливо для всіх симетричних аеродромів. Визначаємо місце, де момент качки дорівнює нулю як центр тиску (іноді його називають центром підйому) і визначаємо місце, де коефіцієнт качкового моменту постійний зі зміною кута атаки як аеродинамічний центр. Ми розглянемо ці далі трохи пізніше. Для симетричного аеропрофілю центр тиску та аеродинамічний центр знаходяться на c/4.

Тепер давайте подивимося на сюжет Б для аеропрофілю 0012. Цей графік відображає результати випробувань на коефіцієнт опору та коефіцієнт моменту та відображає їх у порівнянні з коефіцієнтом підйому, а не кутом атаки. Отже, щоб знайти коефіцієнт опору під певним кутом атаки, потрібно спочатку знайти значення C _L під цим кутом атаки, а потім використовувати його, щоб знайти C _D.

Знову на цій ділянці є різні набори даних для різних значень числа Рейнольдса і шорсткості. Зверніть увагу, що C _D є найменшим під нульовим кутом атаки для цього симетричного аеропрофілю, як і слід було очікувати, і що при збільшенні кута атаки C _D збільшується. Крива моменту на цій ділянці призначена для коефіцієнта моменту в аеродинамічному центрі, а не для c/4, як на графіку зліва. Однак, як зазначалося вище, для симетричного аеродинамічного центру аеродинамічний центр знаходиться на чверті хорди, тому вони тут однакові.

Наступний сюжет в додатку А, малюнок A-2 (A&B), показує аналогічні дані для аеропрофілю NACA 2412. Як і аеропрофіль 0012, ця форма має 12% товщини, але тепер вона має невеликий (один відсоток) розвал з максимальним розгином, розташованим на 40% хорди. Таким чином, ми можемо порівняти ці ділянки з першими, щоб побачити ефект доданого розвалу. Дивлячись на все ті ж речі, згадані вище, ми бачимо, що аеропрофіль тепер має позитивний коефіцієнт підйому (0,15) під нульовим кутом атаки і що нульовий кут підйому атаки тепер мінус один градус. C _Lmax все ще близько 1.6 для нерозкльошеного крила, але з відхиленням клапана він трохи збільшився від симетричного корпусу. Коефіцієнт моменту пітчингу більше не дорівнює нулю при c/4, але він все ще постійний, тепер при значенні близько - 0,025; тобто трохи носом вниз момент качки. Оскільки момент качки на c/4 все ще постійний, ця точка все ще є аеродинамічним центром, але вона вже не є центром тиску. Мінімальний коефіцієнт опору приблизно такий же, як і для симетричного крила, і він все ще мінімальний під приблизно нульовим кутом атаки, але це вже не при нульовому коефіцієнті підйому.

Ми можемо побачити результат подальшого збільшення розвалу до двох відсотків на ділянках для аеропрофілю NACA 2412. Немає даних про прогин щитка, включених в ці ділянки. У цьому сюжеті ми бачимо, що момент качки продовжує збільшуватися негативно (носом вниз), оскільки розвал збільшується, і що мінімальний коефіцієнт опору також почав збільшуватися. Нульовий кут підйому атаки і підйом під нульовим кутом атаки, як видно, продовжують збільшуватися в величині, оскільки розвал додається, як теорія припускає.

Наступні графіки, Рисунок A-3 (A&B), для NACA 2415 показують дуже незначні зміни в поведінці аеропрофілю зі збільшеною товщиною від 12% до 15%, але для секції NACA 2421 ми бачимо, що додана товщина призводить до більш раннього стійла, зменшився C _Lmax, підвищений коефіцієнт опору, а в нелінійному моменті варіація коефіцієнта з кутом атаки близько чверті хорди. Це може припустити нам, що 21% товщина трохи занадто товста.

Дані (рис. A-4 (A&B) для аеропрофілю NACA 4412 продовжують ілюструвати тенденції, розглянуті вище, дивлячись на ефект додавання більшої кількості розвалу.

Останні два набори сюжетів, Малюнки А-5 та А-6, призначені для різного дизайну аеропрофілю NACA 6-серії, форму, яку ми обговоримо спочатку, перш ніж дивитися далі на графіки.

NACA випробував широкий спектр форм аеропрофілю в своїх чотиризначних дослідженнях серії. Однак існували деякі обмеження для варіацій форми, які можна було отримати за допомогою чотиризначного позначення. Вони не могли, наприклад, подивитися на аеропрофіль з максимальним розгином на 25% акорду, лише 20% або 30%. Отже, вони продовжували розробляти 5-значну серію аеродинамічного профілю. Пізніше вони розглянули серію аерофольги, призначену для оптимізації використання ламінарного та турбулентного потоку в прикордонному шарі для мінімізації опору, і розробили аеродинамічні панелі 6-ї серії. Давайте розглянемо обидва з них.

5-значний ряд NACA використовував той самий розподіл товщини, що і чотиризначний ряд, але дозволив більше гнучкості у визначенні положення максимального розвалу. Він також намагався пов'язати кількість розвалу і першу цифру в позначенні аеропрофілю з «конструкцією C _L». Конструкція C _L - це коефіцієнт підйому, який розглядається як оптимальний для цілей продуктивності даного літака. Транспорт на великі відстані може мати розрахунковий коефіцієнт підйому близько 0,3, тоді як винищувач може мати більш високу конструкцію C _L. Приклад 5-значного аерокрила NACA наведено нижче з поясненням системи нумерації:

НАКА 23021

2 — максимальний розвал приблизно 0,02, а конструкція C _L дорівнює 2 х 0,15 = 3,0

30 - положення максимального розвалу (0.30/2) разів хорда або 0.15c

21 - максимальна товщина становить 0,21c

NACA 6-серія (зверніть увагу, що це просто називається «шість» серія, а не шестизначний ряд, хоча більшість номерів позначення мають шість цифр) була розроблена в 1930-х роках в спробі спроектувати серію форм аеродрому, який оптимізував області ламінарного і турбулентного потоку в прикордонний шар на крилі. Як ми вже обговорювали раніше, ламінарний потік у прикордонному шарі є низьким потоком тертя, і це добре; однак ламінарний потік поганий при опорі поділу потоку, а поділ призводить до високого опору та низького підйому. Турбулентний прикордонний шар набагато краще протистоїть поділу потоку, ніж ламінарний, але має більший опір тертя.

Поділ потоку набагато більш імовірно, коли потік сповільнюється (де тиск збільшується, відомий як «несприятливий» градієнт тиску, оскільки ймовірно поділ). Потік над аерофольгом зазвичай прискорюється над передньою частиною форми до точки її мінімального тиску, який зазвичай знаходиться приблизно в точці максимальної товщини. Тут безпечно мати ламінарний потік, оскільки потік навряд чи намагатиметься відокремитися. Якщо ми хочемо більше ламінарного потоку і, отже, більшої частини аерокрила з низьким опору тертя, ми можемо перемістити максимальну точку товщини більше до задньої частини аеродрому. Ідея полягає в тому, щоб отримати якомога більшу площу ламінарного потоку, а потім дозволити прикордонному шару перейти до турбулентного потоку, перш ніж товщина почне зменшуватися, тому турбулентний прикордонний шар буде чинити опір поділу. Це призводить до аеродинамічного профілю з меншим радіусом передньої кромки, ніж старі конструкції, і з максимальною товщиною далі назад.

Дві такі форми 6-серій намальовані як частина своїх графіків даних NACA у Додатку А, аеропрофілі NACA 65 ₁ -212 та 65 ₁ -412. Одна річ, яка відразу очевидна при порівнянні цих двох графіків даних з даними NACA 4-значного аеропрофілю - це «відро» в центрі кривих коефіцієнта опору на графіках правої руки. Це так зване «відро для перетягування» характерно для аерозолів 6-ї серії. Всі ці аерокрилі мають область кута атаки або коефіцієнта підйому, над яким опір значно нижче, ніж при інших кутах атаки. Це діапазон кута атаки, де ламінарний потік може існувати на значній частині передньої частини аеропрофілю, що дає зменшення опору тертя.

Система нумерації аеродинаміків серії 6 розроблена, щоб допомогти дизайнеру/аеродинаміку вибрати найкращий аеродинамічний профіль для роботи, розповівши, де знаходиться центр «ковша для перетягування», і розповівши ступінь (ширину) цього ковша для перетягування. Іншими словами, якщо дизайнер хоче, щоб крило з секцією аеропрофілю, яке дає проектний коефіцієнт підйому 0,2 він або вона хоче, щоб центр ковша перетягування був на C _L 0,2, тому літак зможе виконувати свою проектну місію при мінімально можливих умовах опору. Значить, одне з чисел в позначенні 6-ї серії говорить C _L для центру ковша перетягування. Давайте подивимося на одне з цих позначень аеропрофілю і подивимося, що означають цифри.

НАКА 65 ₁ -212

6 — це лише позначення «серії»

5 - мінімальне місце тиску при нульовому підйомі знаходиться на 50% хорди

1 - це індекс, який може відображатися або не відображатися в позначенні серії 6. Це означає, що ширина «ковша перетягування» поширюється на діапазон C _L 0,1 вище і нижче конструкції C _L

2 — конструкція C _L дорівнює 0,2

12 — як завжди, максимальна товщина яка% хорди

Тепер, якщо ми знову подивимося на дані для вищевказаного аеродрому, ми бачимо, що ковш перетягування дійсно по центру з коефіцієнтом підйому близько 0,2 і ковш поширюється принаймні C _L діапазон 0,1 по обидва боки від його центру. Аналогічно, якщо ми подивимось на ділянки для NACA 65 ₁ -412, ми виявимо, що ковш перетягування знаходиться далі вправо і по центру приблизно C _L 0,4.

Більш детальне порівняння цих 6-серійних аеродинамічних даних з даними 4-значних серій покаже, що не все краще. Аерозолі серії 6 часто затримуються трохи раніше через їх менші радіуси передньої кромки і, отже, мають трохи нижчі значення C _Lmax, ніж їх попередні аналоги. Також їх коефіцієнти опору поза діапазоном опорного ковша можуть бути вищими, ніж звичайні аерозолі. Як і в усьому, в реальному житті поліпшення в одній сфері часто супроводжуються штрафними санкціями в інших. Тим не менш, аерозолі 6-ї серії мають відмінні конструкції і до сих пір використовуються на багатьох літаках.

1.17 Момент пітчингу

Перш ніж ми подивимося далі на розвиток аеродинамічного профілю, ми повинні трохи відступити і подивитися далі на дві речі, згадані раніше, аеродинамічний центр і центр тиску. Це два важливих моменти на аеродромі, які залежать від поведінки моменту качки. Момент повинен бути посиланий на точку, і це трапляється, дуже значущі моменти, про які можна посилатися на момент качки на аеродромі або крилі.

Момент на аеродромі пов'язаний в першу чергу з тим, як здійснюється підйом по фігурі. Перетягування також сприяє моменту, але набагато меншою мірою. На дозвукових швидкостях підйом на більшості аерозолів вище на передній частині форми, ніж на задній і може виглядати приблизно так:

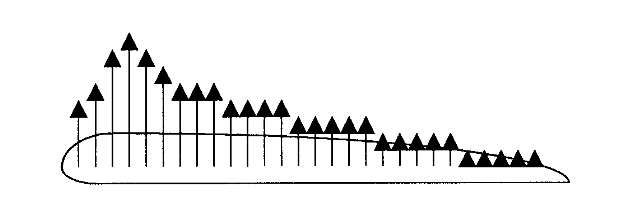
Вертикальні стрілки вздовж профілю аеропрофілю представляють розподіл тиску. Початковий пік утворюється поблизу розташування чверті хорди, після чого тиск знижується до нуля на задньому краї. — Малюнок 1.18: Тип розподілу тиску

Якщо ми вирішимо поговорити про момент пітчингу про передній край аеропрофілю, момент завжди буде носом вниз або проти годинникової стрілки. Якщо ми підсумуємо моменти в якийсь момент приблизно на півдорозі назад вздовж хорди момент буде носом вгору або за годинниковою стрілкою, оскільки сили підйому ліворуч більше, ніж ті, що знаходяться праворуч. Очевидно, що між переднім краєм аеропрофілю та його центром є якась точка , де моменти будуть дорівнювати нулю. Це був би центр тиску. Це може бути цікаво і корисно знати, де це місце, оскільки це, здається, є природною точкою балансу або роду. Єдина проблема полягає в тому, що ця позиція може переміщатися, коли аеродром змінює кут атаки. Наприклад, при більш високому куті атаки ще більше підйомника може бути вироблено біля передньої частини аеропрофілю, а центр тиску буде рухатися ближче до носа аерофольги.

Як виявляється, згідно з аеродинамічною теорією, яку ви вивчите в більш пізньому курсі, є ще один момент, який представляє ще більший інтерес, аеродинамічний центр. Це точка, де коефіцієнт моменту (не сам момент) постійний в широкому діапазоні кута атаки. Основна аеродинамічна теорія скаже нам, що це приблизно на чверті хорди аеропрофілю в дозвуковому потоці. Це було розглянуто для аеродромів, дані яких наведені в Додатку А.

Теорія також покаже, і експеримент перевірить, що для симетричного аеропрофілю, такого як форма NACA 0012 в додатку А, аеродинамічний центр і центр тиску знаходяться в одному місці. Іншими словами, для симетричних аеродинамічних профілів в аеродинамічному центрі момент качки не тільки постійний, але і дорівнює нулю. Це робить аеродинамічний центр дуже зручним місцем для розміщення основних елементів конструкції або використання в якості точки балансу для контрольних поверхонь.

1.18 Розвал і заслінки, а також політ на зниженій швидкості

Ми бачили в даних Додатка А, що зі збільшенням розвалу крила його аеродинамічні показники змінюються. Дивлячись на дані для аеропрофілів NACA 0012, 1412 і 2412, ми побачили, що як розвал (позначений першим терміном в NACA чотиризначної системи нумерації) збільшується крива підйому вліво, даючи більший коефіцієнт підйому при нульовому куті атаки, все більш негативний кут атаки для нульового підйому. коефіцієнт, і повільно зростаюче значення максимального коефіцієнта підйому. Це супроводжується незначним збільшенням коефіцієнта опору та негативним збільшенням коефіцієнта качінгового моменту в аеродинамічному центрі при збільшенні розвалу. У пізніших курсах аеродинаміки ви дізнаєтеся, як передбачити ці зміни, які є результатом модифікації форми лінії розвалу аеродинаміки. Зараз очевидно, однак, що збільшення розвалу може дати більш високі коефіцієнти підйому, і як дизайнер літака, так і пілот, можливо, побажають скористатися цим. Одним з видів польоту, де це стає дуже корисним, є політ на низькій швидкості, особливо при зльоті та посадці.

Для польоту підйомник літака повинен дорівнювати його вазі.

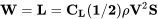
$Ш = Л = СЛ (1/2) ρV2S$

Цей зв'язок говорить про те, що підйом походить від чотирьох речей, коефіцієнта підйому, щільності, швидкості та площі форми крила. Ми нічого не можемо зробити з щільністю, вона поставляється з висотою, і хоча є способи змінити площу крила під час польоту літака, вони часто недоцільні. Зауважимо, що швидкість є потужним фактором, оскільки вона знаходиться в квадраті.

Рівняння вище по суті говорить нам, що якщо ми хочемо літати з меншою швидкістю з заданим крилом і висотою, ми повинні збільшити коефіцієнт підйому. Ми можемо зробити це певною мірою, оскільки збільшуємо кут атаки від нульового кута підйому атаки до кута для стійла, але стійло визначає нашу межу.

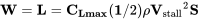
$Ш = L = Кл Макс (1/2) ρ V Сталь 2S$

Ми, звичайно, не хочемо намагатися літати на C _Lmax, тому що ми зупинимося, але швидкість стійла визначає мінімальну межу для нашого можливого діапазону швидкості польоту на заданій висоті. Якщо ми хочемо літати з меншою швидкістю, нам потрібно збільшити значення C _Lmax. Графіки в Додатку А показують нам, що це можна зробити за допомогою стулок. На сюжеті для аеродрому NACA 1412 ми бачимо, що відхиляючи розщеплену заслінку довжиною 20% хорди аеропрофілю до кута 60 градусів, ми можемо збільшити максимальний коефіцієнт підйому з 1,6 до 2,5, зміна, яка б знизила нашу швидкість стійла на 20 відсотків. Це означає, що ми можемо літати на 20% меншій швидкості.

Це потужний ефект, але він не безкоштовний. Супроводжується великим збільшенням коефіцієнта опору і величезною зміною моменту качки. Це може означати необхідність більшого горизонтального стабілізатора або канарди, щоб протистояти зміні тону, і нам потрібно буде мати справу з перетягуванням.

У перші дні польоту реальної потреби в заслінках не було. Літаки літали на швидкостях дуже повільно за сьогоднішніми мірками, і їх стійлові швидкості часто були дуже низькими через великі площі крил. Але як дослідження показали, як зменшити опір літака і кращі двигуни давали все більше потужності і тяги не стільки площі крила потрібно було круїз на результаті більш високих швидкостей. Літак дизайнери виявили, що зробити літак круїз на більш ніж 200 миль/год і все ще приземлитися на щось на зразок 60 миль/год або менше було проблемою. Швидкість посадки важлива, оскільки вона безпосередньо пов'язана з гальмівним шляхом і необхідною довжиною злітно-посадкової смуги. Більш висока швидкість посадки також може збільшити ризик аварій на посадці.

Більшість літаків круїтимуть з коефіцієнтом підйому приблизно від 0,2 до 0,3, а кращі дозвукові аеродроми матимуть C _Lmax не вище 1,8. Ці два фактори визначають проблему високошвидкісного круїзу і низької швидкості посадки.

У 1933 році компанія «Боїнг» вивела авіалайнер Boeing 247, ґрунтовно сучасний для свого часу літак, який скористався перевагами всього накопиченого прогресу в проектуванні двигунів і планера. Його крейсерська швидкість становила 188 миль/год на висоті 8000 футів. 247 важив 13,650 фунтів і мав площу крила 836 футів ². Швидкий розрахунок його коефіцієнта круїзного ліфта дає C _L = 0,23, розумне значення. У той час існуючі злітно-посадкові смуги вимагали швидкості посадки близько 60 миль/год, а розрахунок коефіцієнта підйому 247 на рівні моря на рівні 60 миль/год дає 1.77, майже майже максимум для звичайного крила.

Компанія Douglas Aircraft Company (нині входить до складу Boeing) вирішила побудувати більший і комфортний авіалайнер і вийшла з DC-1, прототипом літака та виробничою моделлю DC-2. DC-2 важив на 36% більше, ніж 247 на 18,560 фунтів і мав трохи вищу площу крила 939 футів ², але він круїздив приблизно на тій же швидкості та висоті, що і його конкурент. Круїз C _L для DC-2 виходить приблизно на 0,27, вище, ніж 247 через його значно більшої ваги. Таке більш високе «завантаження крила» дало пасажирам DC-2 більш комфортну їзду, ніж 247.

Для посадки DC-2 зі швидкістю 60 миль/год потрібно C _L близько 2,15, занадто високий для нормального крила. Рішення полягало в тому, щоб додати заслінки, даючи додатковий розвал і більш високий C _Lmax, коли це необхідно для посадки та зльоту. Це дозволило більшому, більш зручному DC-2 літати так само швидко, як 247 і все ще приземлятися і злітати у всіх комерційних аеропортах свого дня. DC-2 та його ще більший та комфортніший брат, DC-3, продовжували революцію в авіаційній галузі.

Слід зазначити, що великі відхилення заслінки використовуються при посадці, де доданий опір може бути фактично вигідним, а менші прогини використовуються при зльоті, де менший опір і швидке прискорення є обов'язковими.

Boeing 247 показано рулювання на злітно-посадковій смузі з його подвійними гвинтовими двигунами, встановленими на передній частині крил біля фюзеляжу. Показаний літак United Air Lines, з показаними 5 пасажирськими вікнами, кожен з яких має прямокутну форму, але із закругленими кутами, а не гострими кутами. Крім того, крила мають велику площу поверхні разом із закругленим вертикальним хвостом в задній частині літака. — Малюнок 1.19: Боїнг 247

DC-2 схожий на раніше показаний Boeing 247, з точки зору розміщення двигуна і великої площі крила. Однак DC-2 має 7 пасажирських вікон із закругленими кутами, поряд з менш закругленою вертикальною хвостовою частиною, дві третини з яких є частиною відхиляється керма. Цей літак показаний в процесі посадки на аеродромі. — Малюнок 1.20: Дуглас DC-2

Існує безліч видів стулок. Є як передній край, так і задній край закрилки і масив варіацій на обох. Аеродинамічна теорія говорить нам, що збільшення розвалу є найбільш ефективним, коли це робиться поблизу заднього краю аеропрофілю, отже, задній край заслінки є основним типом заслінки, що використовується на крилах. Прогин практично будь-якого типу заднього краю заслінки від простої плоскої пластини до складної, багатоелементної системи заслінки змістить «криву підйому» вліво і збільшить C _Lmax. Деякі закрилки заднього краю мають прорізи та кілька елементів, які допомагають контролювати потік над заслінками та запобігають поділу, щоб дати ще більший коефіцієнт підйому, і часто ці заслінки розгортаються таким чином, щоб тимчасово додати додаткову площу крила.

Передні крайові клапани мало роблять для переміщення кривої підйому вліво, але можуть зробити багато, щоб дозволити аеродрому перейти до більш високого кута атаки перед зупинкою, контролюючи потік над «носом» аеропрофілю та затримуючи поділ. Передні крайові стулки часто використовуються при зльоті і посадці в поєднанні з задніми краями заслінки. Кілька літаків були розроблені з передніми краями закрилків або прорізів, закріплених постійно в крилі, щоб дати їм нижчі швидкості стійла.

Ефекти як переднього, так і заднього краю закрилків показані на наступному малюнку.

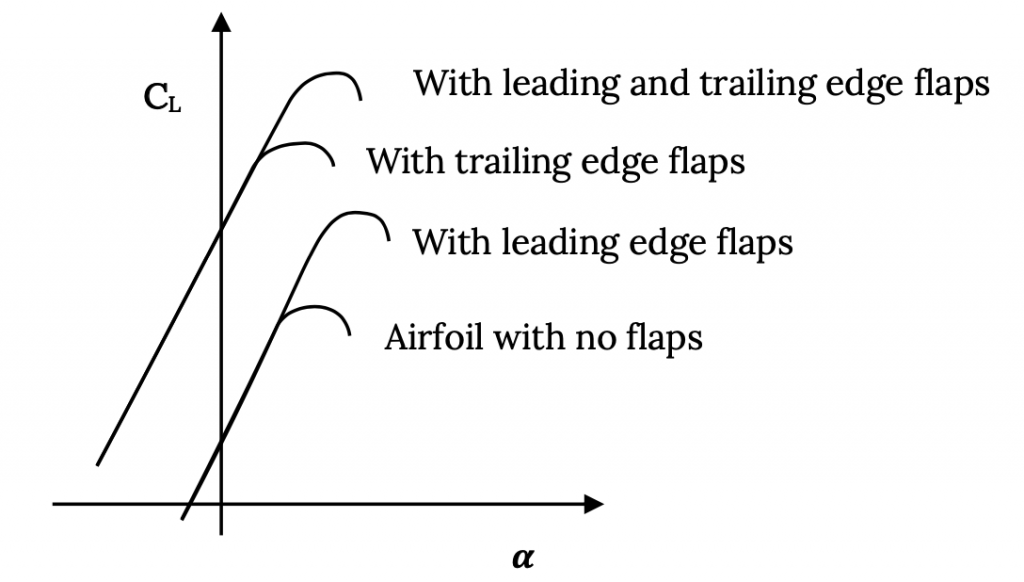
Чотири криві показані для cap C sub cap L як функція альфа, подібно до малюнка 1.18 а. аерокрил без закрилків має найнижчий пік, при додаванні лише передніх крайових клаптів подовжує лінію далі і збільшує максимальну кришку C sub cap L. Додавання лише закрилків заднього краю зміщує лінію вертикально на графіку до більш високого y-перехоплення та max cap C sub cap L, з додаванням додаткових кіл переднього краю також продовжить цю лінію, ще більше збільшуючи максимальну кришку C sub cap L. — Малюнок 1.21: Типові ефекти головного і заднього краю клаптя

Наступна таблиця перелічує типові величини коефіцієнта підйому з та без як передніх, так і задніх кромок для аеропрофілю «Clark Y». Airfoil Clark Y - це відома форма аеродрому, що не є NACA, розроблена Вірджиніусом Кларком. Кларк служив у тій же комісії, що і багато засновників NACA, комісія, яка доручена вивчати європейські секції аеродрому після Першої світової війни, і, використовуючи більшу частину тієї ж інформації, яку NACA використовував для розробки своїх оригінальних 4-значних аеродромів, Кларк розробив Clark Y та інші аеродроми як частина його докторські дослідження в MIT. У Clark Y Вірджиніус Кларк розробив форму аеродрому з плоским дном, що полегшило його виготовлення, і завдяки цьому та своїм чудовим аеродинамічним характеристикам він широко використовувався для всього, від крил літака до лопатей гвинта.

Профіль аеропрофілю Clark Y показано на графіку з відсотковою хордою на вертикальній осі та логарифмічною віссю відсоткової хорди на горизонтальній осі. Аерофольг починається приблизно з 5 відсотків хорди, зростаючи у формі краплі до максимальної товщини приблизно від 12 до 13 відсотків хорди на довжині 30 відсотків уздовж хорди. Потім він повільно зменшується до нуля на задньому краю. — Малюнок 1.22: Форма аерофольги Clark Y

Таблиця 1.3: Передній край і задній край клаптя і слот ефекти на аерофользі Clark Y

Конфігурація	C Sub Lmax	альфа-суб стійло
Базовий аерозоль Clark Y	1.29	15
з 30% звичайним клапаном при 45°	1,95	12
з «фіксованим» прорізом і без клапана	1.77	24
з прорізом і звичайним клапаном	2.18	19
з 40% заслінкою Фаулера при 40°	3.09	14
з розгорнутим гніздом і клапаном Фаулера	3.36	16

Підводячи підсумок, задня кромка може мати значний «ефект розвалу»; тобто може зміщувати «криву підйому» вліво, збільшуючи нульовий кут підйому атаки і значення C _Lmax. Він також може бути розгорнутий таким чином, щоб тимчасово збільшити площу крила. Клапан переднього краю або слот, ймовірно, не вироблятиме «ефект розвалу» (якщо це робить, це, ймовірно, буде «негативним», трохи зміщуючи «криву підйому» вправо), але допоможе затримати стійло до більш високого кута атаки, незалежно від того, використовується на крилі з закрилками або без них.

1.19 Транзвукові та надзвукові аерокрила та крила

Раніше ми розглядали, як потік може прискорюватися до надзвукових швидкостей над аеродромом або крилом, коли швидкість вільного потоку наближається до швидкості звуку, і як при числах Маха, вищих за деяке «критичне число Маха», уповільнення цього надзвукового потоку назад до дозвукових швидкостей може призвести до раптового потоку. поділ і збільшення перетягування. Існує два способи зменшити цей опір. Один - підмітаючи крило, а інший - розробляючи спеціальну секцію аеропрофілю.

1.20 Розгортка крила

Перший спосіб, знайдений для успішного зменшення опору, що відбувається в режимі трансонічного польоту, - це підмітання крила. Теорія та експеримент показали, що як початок, так і величина збільшення опору були функціями «нормальної складової» вільного потоку числа Маха, M∞. Іншими словами, якщо крило розгорнуто 45 ⁰, нормальною складовою вільного потоку числа Маха є M∞ косинус θ або 0,707.

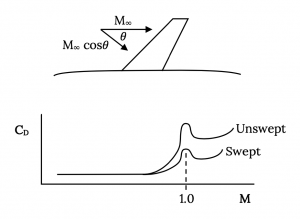
Для крила, розгорнутого назад кутом тета, повітря наближається до числа Маха cap M sub нескінченності. Однак, завдяки розгортці, частина, нормальна до переднього краю крила, є лише ковпачком M sub нескінченності разів косинус тета. Завдяки зниженій швидкості повітря в нормі до крила, результуючий пік коефіцієнта опору ковпачка C sub cap D при ковпачку M sub нескінченності, рівному 1, зменшується. Cap C sub cap D є постійним для низьких чисел Маха, але, як він збільшується, ковпачок C sub cap D збільшується раніше і швидше, ніж змітаються конструкції крила, причому обидва мають округлі піки на ковпачку M sub нескінченності рівну 1, які трохи падають, коли він рухається за межі 1, перш ніж обидва починають знову збільшуватися. — Малюнок 1.23: Загальні наслідки розгортки крила на трансзвуковий підйом опору

Як і майже у всьому, ця перевага розгортки коштує. Підмітання крила також зменшує його коефіцієнт підйому під заданим кутом атаки (зменшує нахил кривої підйому), а вигнутий потік над самим крилом може призвести до передчасного затримання біля кінчиків крила та явища, відомого як «крок вгору»

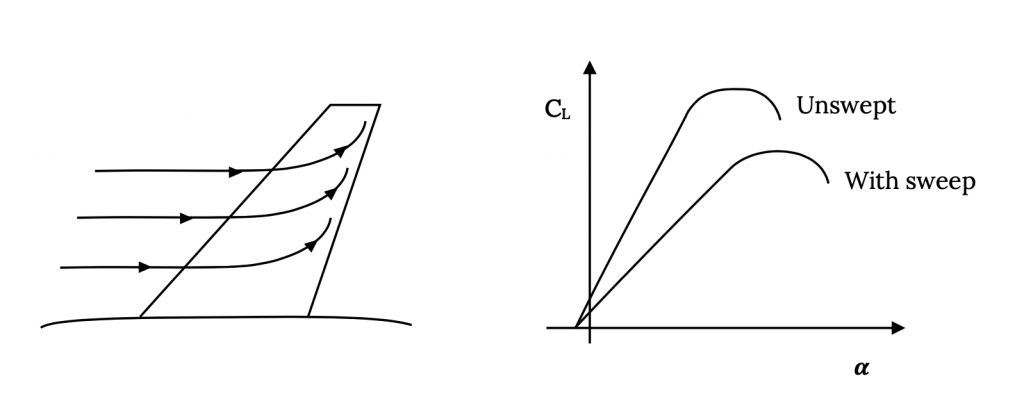
а) Коли повітряний потік наближається до розгорнутого крила, він повернутий до кінчика крила, а не тече прямо через крило. б) Підмітання крила призводить до ліфт-кривої, щоб мати зменшений нахил і ковпачок C sub cap L max, але вище альфа-суб стійло. — Малюнок 1.24: Інші ефекти розгортки крила

Хоча більшість прометаних крил розташовані під кутом до задньої частини літака або змітаються назад, теоретично не має значення, чи крило змітається вперед або в кормі. Кілька ранніх конструкцій крила були намальовані з передніми стріловими крилами, що дозволило лонжерону крила або конструкції проходити через фюзеляж кормової частини кабіни і представляло менше внутрішніх проблем з дизайном, але незабаром було виявлено, що дійсно проблема з вперед підмітали крила. Ця проблема була викликана тим же типом криволінійного потоку, який спричинив стійло наконечника на кормових крилах, за винятком того, що результатом на передньому підмітому крилі був додатковий підйом на кінчиках крила, який, як правило, скручував крила до їх точки розриву на досить низьких швидкостях. Було мало сенсу підмітати крило для зниження трансонічного опору, коли крило зламається задовго до досягнення таких швидкостей, а додаткова вага, необхідна для посилення крила, щоб запобігти невдачі, зробили літаки занадто важкими. Ця проблема була остаточно вирішена в 1970-х роках із застосуванням композитних конструкцій на основі тканини, які могли бути розроблені таким чином, що крило зміцнювалося, коли намагалося скрутити. Експериментальний літак X-29 успішно довів, що прометані вперед крила дійсно можуть бути використані в трансзвукових потоках.

1.21 Надкритичні аеродроми

Інший метод, який використовується для зменшення трансонічного опору підйому на крилі, був розроблений Річардом Уіткомбом в дослідницькому центрі НАСА-Ленглі в 1960-х роках Доктор Віткомб істотно змінив звичайний розділ аеродрому, щоб зробити три речі. Він збільшив «округлість» передньої кромки аеропрофілю, щоб дати більш поступове прискорення потоку до швидкості нижче, ніж звичайні форми аеропрофілю, тому, коли надзвуковий потік призвів до поверхні, він був слабкішим. Він зменшив розвал крила в середній області хорди, щоб вирівняти верхню поверхню і дозволити довшу область цього слабшого надзвукового потоку, перш ніж дозволити йому сповільнитися, даючи менше поділу та опору. Нарешті, щоб компенсувати ліфт, який був втрачений, проектуючи для більш повільного потоку верхньої поверхні, Whitcomb розробив його аерофольгу зі значним «кормовим розвал» на його нижній поверхні, зазначивши, що розвал має дуже потужний ефект акуратний задній край аеропрофілю. Результатом став аеропрофіль, дещо схожий на той, що нижче, який давав чудові аеродинамічні показники зі зменшеним трансонічним підйомом опору. Цей тип аерокрила називається аерофольгом Whitcomb або «надкритичним» аерофольгом.

Надкритичний аеропрофіль має подібну закруглену передню кромку до стандартного аерофольгу, але залишається відносно постійною товщиною за межами розташування чверті хорди, поки не досягне приблизно двох третин своєї довжини. У цей момент верхня поверхня трохи повертається вниз, але нижня поверхня повертається вгору, щоб зменшити товщину, потім назад вниз, щоб отримати гострий задній край з точкою вниз. — Малюнок 1.25: Надкритична форма аеропрофілю

Як виявилося, цей аерозоль був відмінною конструкцією для всіх діапазонів польоту, єдиним його недоліком є тенденція до великого моменту качки за рахунок кормового нижнього розвалу. Наступні конструкції зменшили цю проблему і варіанти цієї конструкції використовуються практично на кожному типі літаків сьогодні.

Під час обговорення Річарда Віткомба та трансонічного потоку слід також згадати його дизайн фюзеляжу «коксової пляшки». На початку 1950-х років, коли реактивні винищувачі наближалися до Маха 1 в можливості, трансонічне опір підйом всього літака продовжував бути проблемою в «порушенні так званого звукового бар'єру». Convair і ВПС сподівалися, що новий, високо прометаний, дельта-крило винищувач призначений F-102 зможе регулярно літати на надзвукових швидкостях; однак два прототипи літаків не змогли досягти Маха 1. Уіткомб зрозумів, що зі швидкістю звуку повітря не може бути стиснутий далі і потребує деякого місця, щоб піти, або він просто виштовхне назовні з площини, витісняючи інший потік повітря і викликаючи опір. Він запропонував переробити фюзеляж F-102 зі зменшеним перетином поблизу крила, щоб дозволити цьому надзвуковому повітрю місце йти, не відштовхуючи зовнішні потоки. Фюзеляж «оси-талія» або «кокс-пляшка» був результатом, і дизайн, який раніше не міг досягти швидкості звуку, досяг 1.22 Маха під час першого польоту.

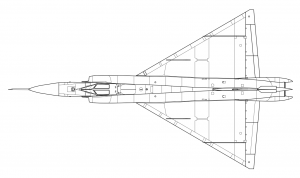
Вид зверху F-102 показує звуження фюзеляжу на дельта крила розширюються до задньої частини літака. — Малюнок 1.26a: Конвейр Ф-102 «Дельта кинджал»

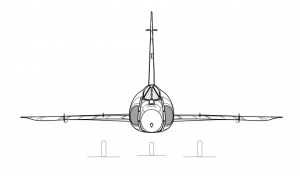
Вид спереду показує дельта-крила лише трохи звужені від кореня до кінчика і, здається, вирівняні з центром фюзеляжу. — Малюнок 1.26b: Конвейр F-102 «Дельта кинджал»

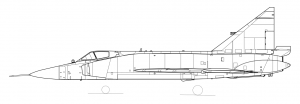
Вид збоку показує крила на лінії з кінчиком носа літака, і strentch від коротких шляхів позаду кабіни, приблизно до однієї третини довжини хвоста. — Малюнок 1.26c: Конвейр Ф-102 «Дельта кинджал»

1.22 Тривимірна аеродинаміка

Більшість речей, обговорюваних в попередніх розділах, були двовимірним явищем, таким як дизайн секції аеродинамічного профілю, ефекти розвалу і т.д. розгортка крила була винятком. Але є багато інших варіацій плану крилаформи і форми, які будуть впливати на аеродинамічні показники крила. Почнемо з погляду на Співвідношення сторін.

Крило, яке виробляє підйом, повинно мати менший тиск на його верхню поверхню, ніж на нижню поверхню. На кінчиках крила нічого не заважає повітрю з нижньої поверхні намагатися обійти кінчик крила до верхньої поверхні, де нижній тиск діє як вакуум. Результатом є деяка втрата підйому біля кінчика крила. Ідеальне крило матиме такий же підйом від кінчика крила до кінчика крила, але справжнє крило не робить.

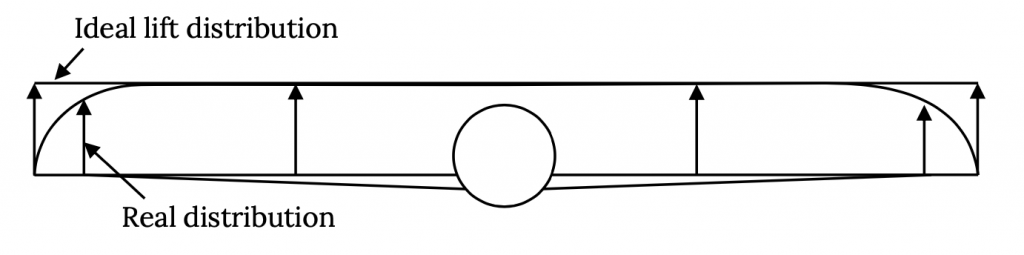
Ідеальний розподіл підйому виглядає як постійний підйом від кінчика крила до кінчика крила. Реальний розподіл є еліптичним, при цьому навантаження швидко зростає від нуля на кінчиках до тієї ж постійної величини, що і ідеальний розподіл, коли він рухається всередину до фюзеляжу. — Рисунок 1.27: Ідеальний (2-D) та реальний (3-D) розподіл підйому на крилі

Ця втрата підйому відчувається на деякій відстані вборту кінчиків крила. Питання в тому, на який відсоток площі крила це впливає, і це буде залежати від співвідношення сторін крила, AR.

Співвідношення сторін - це міра розмаху крила, розділена на його «середню» або середню хорду. Він також може бути виражений через квадрат прольоту і площиніформу площі.

АР = б ² /с = б/с _{середнє}

де b = розмах крила, S = плоска площа, c = хорда

Щоб зрозуміти, чому співвідношення сторін є важливим, ми можемо подивитися на дві різні форми плану крила однієї площі, але різні пропорції.

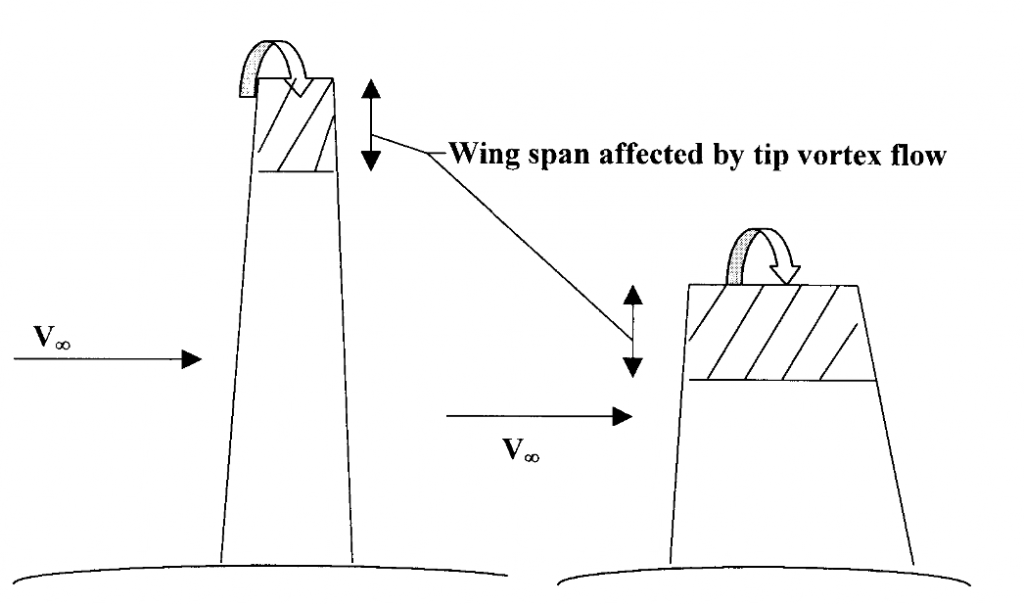
а) Крило з більш високим співвідношенням сторін через довгу і вузьку форму має лише невелику частину своєї зовнішньої області, ураженої вихорами кінчика крила. б) Крило з нижнім співвідношенням сторін, завдяки короткому широкому крилу, має більшу частину своєї площі, уражену вихорами кінчика крила. — Малюнок 1.28: Високе крило AR зліва має меншу площу, на яку впливає обтік навколо кінчика, і, таким чином, менші втрати підйому, ніж нижнє крило AR праворуч.

Цей потік навколо кінчика крила призводить до двох інших проблем, вироблення опору, що називається індукованим перетягуванням, і створення закрученого потоку, схожого на торнадо, який називається вихровим наконечником крила за кінчиком крила, який може становити небезпеку для наступних літаків.

Задні вихори (один вихор з кожного кінчика крила) можуть тривати на милі позаду літака, і «сила» вихорів буде залежати від ваги генеруючого літака. Наступний літак, особливо невеликий, може виявитися раптово перевернутим догори дном (або гірше), якщо він зіткнеться з одним із цих вихорів. Це особливо небезпечно поблизу землі і є однією з причин необхідного часу поділу між посадкою і зльотом літаків в аеропортах.

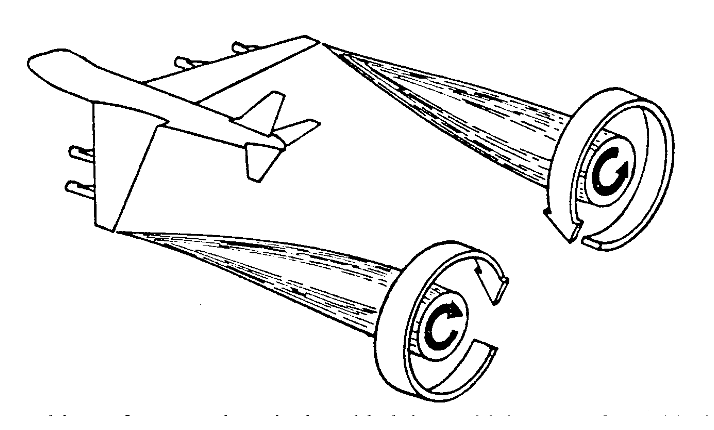
Кожен кінчик крила проливає вихор, який обертається до фюзеляжу. При погляді з літака: за годинниковою стрілкою від лівого крила та проти годинникової стрілки від правого крила. — Малюнок 1.29: Задні вихори

3-D проблема, що викликає занепокоєння тут, - це доданий опір, який походить від цього потоку навколо кінчиків крила та зменшеного підйому. Через цей потік коефіцієнт підйому на 3-D крилі буде нижчим при заданому куті атаки, ніж 2-D секція аеропрофілю тієї ж форми. Аеродинамічна теорія може бути використана для обчислення 3-D ефекту як функції плоскої форми крила, і цей ефект можна охарактеризувати як ефект співвідношення сторін. Кажуть, що 2-D секція аеропрофілю має нескінченне співвідношення сторін, а для теорії 2-D випадку дає нахил для «кривої підйому» (DCL/Dα) 2π. Для 3-D випадку, коли співвідношення сторін кінцеве, нахил кривої підйому буде виявлено, що зменшується зі зменшенням співвідношення сторін.

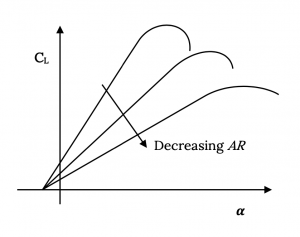
Коли ковпачок А ковпачок R зменшується, нахил кривої підйому зменшується, а поворот на ковпачку C sub cap L max згладжується. — Малюнок 1.30: «нахил» кривої підйому зменшується у міру зменшення AR

Доданий опір в 3-D походить від того ж явища, що викликає підйом. Ми визначаємо життя як силу, перпендикулярну швидкості вільного потоку. Індукований опір - це сила, яка перпендикулярна швидкості «вниз», викликаної потоком навколо кінчика крила. Ця швидкість змиву невелика порівняно з потоком вільного потоку, а індукований опір відповідно невеликий, але це все ще сила, яку нам потрібно зрозуміти та мати справу.

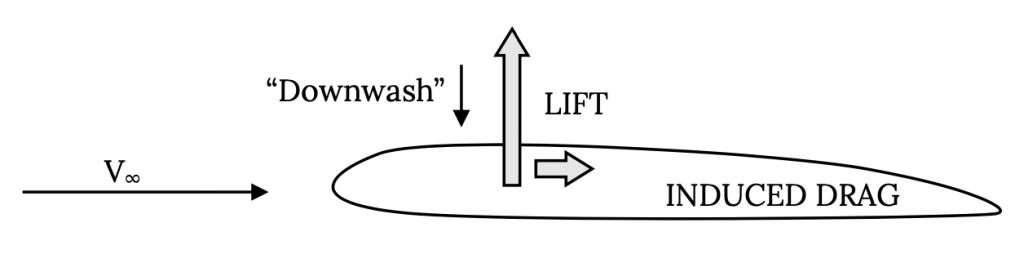
Коли повітря наближається до аеропрофілю горизонтально при швидкості ковпачка V sub нескінченності, вертикальна сила підйому протистоїть набагато менша сила від кінчика крила, відома як вниз. Індукована сила опору паралельна напрямку швидкості. — Малюнок 1.31: Зниження та індуковане опір

Теорія покаже індукований коефіцієнт опору C _Di бути:

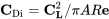
$CDI = CL2/πє$

З цього видно, що у міру збільшення AR індукований опір зменшується і що в 2-D випадку, коли теоретичне співвідношення сторін є нескінченністю, коефіцієнт індукованого опору дорівнює нулю. Але, як щодо іншого члена в рівнянні, е?

Він називається «коефіцієнтом ефективності Освальда». Значення e буде десь між нулем і одиницею, причому один з них є найкращим або «мінімальним індукованим перетягуванням» випадку. Теорія покаже, що е є функцією способу підйому діє вздовж прольоту крила, який є функцією декількох речей, включаючи форму форми крила, розгортки крила, скручування крила, конусність, різні секції аеродинамічного профілю, що використовуються по всьому прольоту і т.д. вивчення цієї теорії покаже, що найкращий випадок, коли e = 1.0 виникає, коли підйом розподіляється по розмаху крила еліптичним способом. Цей мінімальний індукований випадок перетягування часто називають еліптичним корпусом розподілу ліфта.

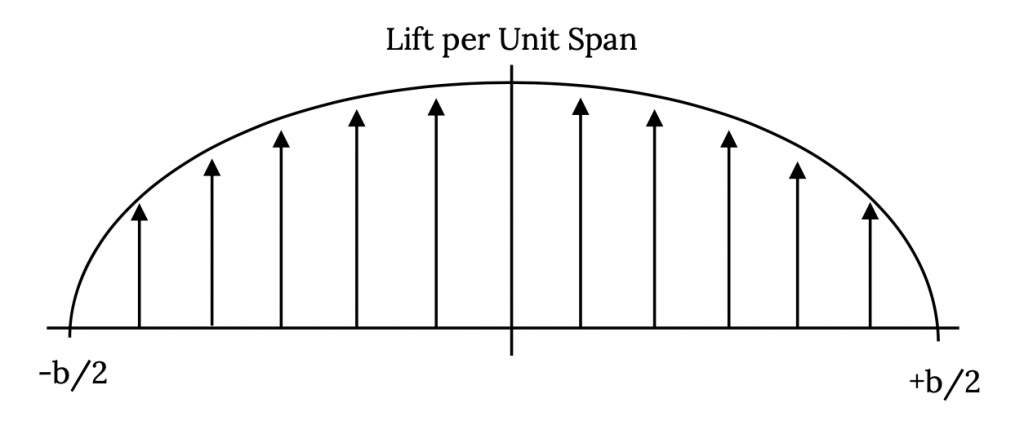
Показано ідеально еліптичний розподіл підйому, який з'являється у вигляді верхньої половини еліпса з 0 на кожному кінчику крила і максимумом, що відбувається посередині. — Малюнок 1.32: Розподіл еліптичного підйому

Існує багато способів отримати еліптичний розподіл ліфта. Найпростішим для візуалізації є те, що там, де форма площини крила має форму еліпса, тобто там, де хорда крила змінюється еліптично уздовж його прольоту. У 1940-х роках багато винищувачів Другої світової війни були побудовані з еліптичними планформами, щоб спробувати мінімізувати індукований опір. Найвідомішим з них став британський літак Spitfire.

Британський Spitfire показаний знизу з великими еліптичними крилами та хвостом, зображеними на видному місці. Розмах крил вказаний як 36 футів 10 дюймів, або 11,23 метрів, а максимальна вага зльоту навантаження вказана як 5784 фунти, або 2624 кілограми. — Малюнок 1.33: Британський літак «Spitfire»

Можна отримати еліптичний або майже еліптичний розподіл ліфта іншими способами з правильною комбінацією конусності крила, скручування, і розгортки або шляхом зміни секції аерокрила використовується, коли ви виходите з прольоту. Деякі з цих комбінацій можуть дати значення індукованого коефіцієнта опору при мінімальному або близькому до мінімуму, мінімізуючи труднощі побудови крила. У деяких випадках складна плананаформа потрібна з інших причин, таких як «скритність» або мінімізація радіолокаційної віддачі літака. B-2, «стелс» бомбардувальник, незважаючи на його «пила-зуб» у формі крила, має майже еліптичний розподіл підйому.

Часто скручування є частиною цієї схеми, оскільки вона також може знадобитися для контролю в стійлі. Оскільки контрольні поверхні, що використовуються для контролю рулону, елерони, знаходяться поблизу кінчиків крила, які ми хочемо спроектувати крило, щоб підвісна частина крила не затихне, коли внутрішня секція починає зупинятися. З цієї причини частина крила біля кінчика часто скручується, щоб надати йому менший кут атаки, ніж решта крила. Деякі літаки використовують різні секції аеропрофілю біля кінчика, ніж на решті крила з цієї причини.

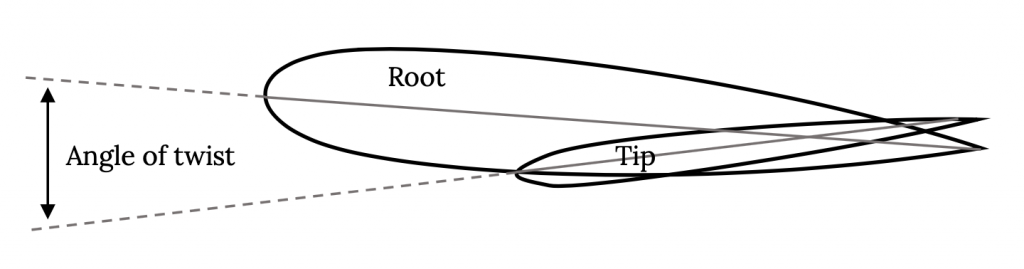
Показано, що наконечник аеродинамічних сил має кут атаки нижче, ніж корінь, за рахунок скручування від аеродинамічних сил. Різниця між кутом кінчика та кутом кореня визначається як кут закручування. — Малюнок 1.34: Часто крила скручуються, щоб утримати область кінчика від зупинки, коли внутрішнє крило ларьків, а також забезпечити низький розподіл підйому опору по прольоту.

Слід підкреслити, що хоча еліптичний розподіл підйомників є ідеальним аеродинамічно, є й інші фактори, які необхідно враховувати при проектуванні крила. Наприклад, інший розподіл підйомника цілком може бути оптимальним для міцності конструкції або для контролю чуйності. Британський Spitfire був дуже ефективним літаком аеродинамічно через його еліптичної форми крила, але пілоти виявили, що вони не можуть котити винищувач так швидко, як їхні німецькі опоненти в повітряних боях. В результаті прекрасне крило Spitfire було «обрізане» у пізніших версіях, щоб забезпечити більшу швидкість рулону, оскільки в реальному світі повітряної війни маневреність виявилася важливішою, ніж аеродинамічна ефективність та опір.

Слід також підкреслити, що індукований опір - це лише частина перетягування. Цей «перетяг через підйом» не залежить від інших джерел опору, таких як тертя між повітрям та «шкірою» або поверхнею літака або «опору тиску», що походить від нормальної зміни тиску навколо повітряного профілю. Ці інші типи опору повинні бути розраховані з аеродинамічної теорії та теорії «граничного шару», предметів двох курсів пізніше в навчальній програмі.

Домашнє завдання 1

1. Напишіть калькулятор або комп'ютерну програму, щоб знайти стандартні умови атмосфери (тиск, температура і щільність) для будь-якої висоти в тропосфері і стратосфері як в SI, так і в англійській одиницях. Увімкніть список програми та роздруківку для умов кожні 1,000 метрів (одиниці СІ) та кожні 1000 футів (англійські одиниці) до 100 000 футів або 30000 метрів.

2. Бак для стисненого повітря оснащений вікном діаметром 150 мм. U-трубний манометр, що використовує ртуть як робочу рідину, з'єднаний між резервуаром та атмосферою і зчитує 1,80 метра. Яка загальна навантаження діє на болти, що кріплять вікно? Відносна щільність ртуті - 13,6.

3. У певний день рівень моря тиск і температура складають 101 500 Н/м ² і 25°C відповідно. Встановлено, що температура падає лінійно з висотою до -55° C на 11300 метрів і бути постійною вище цієї висоти.

4. Літак без помилок приладу і з висотоміром, відкаліброваним відповідно до специфікацій ISA, має показання висотоміра 5000 метрів. Яка реальна висота літака? Яку висоту показував би висотомір, коли літак приземляється на рівні моря?

Посилання

Таблиці 1.1 та 1.2: Національний консультативний комітет з повітроплавання (1953). НАКА-ТР-1135 і НАКА ТН 1428. Отримано з https://ntrs.nasa.gov/citations/19930091059

Малюнок 1.1: Родинний сірий (2021). «Термінологія аерокрила». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.1_20210804

Малюнок 1.2: Родинний сірий (2021). «Термінологія планформи крила». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.2_20210804

Малюнок 1.3: Родинний сірий (2021). «Деякі форми форми крила». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.3_20210804

Малюнок 1.4: Родинний сірий (2021). «Типовий механічний чутливий висотомір». КУБ.СМ ЗА 3,0. Адаптовано з Вікідоту (2009). «Малюнок 4: Механізм». CC BY-SA 3.0. Оригінал: http://aviationknowledge.wikidot.com/aviation:sensitive-altimeters. Адаптовано: https://archive.org/details/1.4_20210804

Малюнок 1.5: Джеймс Федорович Марчман (2004). «Приклад рівняння Бернуллі». CC ПО 4.0.

Малюнок 1.6: Джеймс Федорович Марчман (2004). «Трубка Піто вимірює загальний тиск». CC ПО 4.0.

Малюнок 1.7: Джеймс Федорович Марчман (2004). «Статична трубка вимірює статичний тиск». CC ПО 4.0.

Малюнок 1.8: Родинний сірий (2021). «Пілот-статичний зонд». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно з https://archive.org/details/1.8-updated

Малюнок 1.9: Родинний сірий (2021). «Індикатор швидкості повітря». CC ПО 4.0. Адаптовано з Пілотного посібника з авіаційних знань Федерального авіаційного управління. Публічне надбання. Оригінал доступний з https://www.faa.gov/regulations_policies/handbooks_manuals/aviation/phak/media/10_phak_ch8.pdf. Адаптовано доступно з: https://archive.org/details/1.9_20210804

Малюнок 1.10: Родинний сірий (2021). «Формування ударної хвилі в «трансонічному» потоці.» CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.10_20210804

Малюнок 1.11: Родинний сірий (2021). «Збільшення коефіцієнта опору біля першого Маха». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.11_20210804

Малюнок 1.12: НАСА (1947). «Дзвін Х-1 46-062 (в польоті)». Публічне надбання. Доступно з https://commons.wikimedia.org/wiki/File:Bell_X-1_46-062_(in_flight).jpg

Малюнок 1.13: Родинний сірий (2021). «Обтікати круговий циліндр». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.13_20210804

Малюнок 1.14: Родинний сірий (2021). «Варіація коефіцієнта опору з числом Рейнольдса для сфери». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.14_20210804

Малюнок 1.15: Родинний сірий (2021). «Визначення знака моменту пітчингу». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.15_20210804

Малюнок 1.16: Родинний сірий (2021). «Взаємозв'язок між підйомом, перетягуванням та швидкістю вільного потоку». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.16_20210804

Малюнок 1.17: Родинний сірий (2021). «Ділянки коефіцієнта підйому та опору проти альфи, показуючи стійло (а)». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.17_20210804

Малюнок 1.18: Джеймс Федорович Марчман (2004). «Тип розподілу тиску». CC ПО 4.0.

Малюнок 1.19: Архіви SDASM (2013). «Боїнг 247». Вікісховище. Доступно з https://www.flickr.com/photos/sdasmarchives/11343397173/

Малюнок 1.20: Бйорн Стрей (2009). «Дуглас DC-2 (PH-AJU) в польоті в аеропорту Бремен Flugtag (3519224016)». CC BY-SA 2.0. Доступно з https://commons.wikimedia.org/wiki/File:Douglas_DC-2_(PH-AJU)_in_flight_at_the_Bremen_Airport_Flugtag_(3519224016).jpg

Малюнок 1.21: Родинний сірий (2021). «Типові ефекти головного і заднього краю клапоть». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.21_20210804

Малюнок 1.22: Джеймс Федорович Марчман (2004). «Форма аерофольги Clark Y». CC ПО 4.0.

Малюнок 1.23: Родинний сірий (2021). «Загальні наслідки розгортки крила на трансзвуковий підйом опору». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.23_20210804

Малюнок 1.24: Родинний сірий (2021). «Інші ефекти розгортки крила (а)». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.24_20210804

Малюнок 1.25: Родинний сірий (2021). «Надкритична форма аеропрофілю». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.25_20210804

Малюнок 1.26: Каболди (2012). «Конвейр Ф-102 Дельта Кинджал». CC BY-SA 3.0. Доступно з https://commons.wikimedia.org/wiki/File:Convair_F-102_Delta_Dagger.svg

Малюнок 1.27: Родинний сірий (2021). «Ідеальний (2-D) та реальний (3-D) розподіл підйому на крилі». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.27_20210804

Малюнок 1.28: Джеймс Федорович Марчман (2004). «Високе крило AR зліва має меншу площу, на яку впливає потік навколо кінчика, і, таким чином, менші втрати підйому, ніж нижнє крило AR праворуч. (а)». CC ПО 4.0.

Малюнок 1.29: Джеймс Федорович Марчман (2004). «Кінцеві вихори». CC ПО 4.0.

Малюнок 1.30: Родинний сірий (2021). ««Нахил» кривої підйому зменшується у міру зменшення AR». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.30_20210804

Малюнок 1.31: Родинний сірий (2021). «Зниз і індукований опір». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.31_20210804

Малюнок 1.32: Родинний сірий (2021). «Еліптичний розподіл ліфтів». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.32_20210804

Малюнок 1.33: Родинний сірий (2021). «Британський літак «Spitfire». CC BY-SA 2.0. Адаптовано з фотографії Сокола (2019). «Обтічник живота Spitfire». CC BY-SA 2.0. Оригінал доступний з https://www.flickr.com/photos/falcon_33/48712711406/in/photostream/. Адаптований доступний з https://archive.org/details/1.33_20210804

Малюнок 1.34: Родинний сірий (2021). «Часто крила скручуються, щоб утримати область кінчика від зупинки, коли внутрішнє крило ларьків, а також забезпечити низький розподіл підйому опору по прольоту». CC ПО 4.0. Адаптовано з Джеймса Федоровича Марчмана (2004). CC ПО 4.0. Доступно за адресою https://archive.org/details/1.34_20210804

<! — pb_fixme —><! — pb_fixme —>