Skip to main content
LibreTexts - Ukrayinska

5.7: Контрольний список глав

  1. Last updated
  2. Save as PDF
  • Page ID
    79274

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Тепер ви повинні мати можливість:

    1. Розпізнати скінченну систему як частину космічного перекладу інваріантної нескінченної системи;
    2. Знайти нормальні режими скінченної системи як лінійні комбінації нормальних режимів космічного перекладу інваріантної нескінченної системи, узгодженої з фізикою меж, шляхом накладення граничних умов;
    3. Охарактеризуйте нормальні режими інваріантної системи просторового перекладу в терміні кутового хвильового числа\(k\);
    4. Знайти дисперсійне відношення, яке пов'язує кутову частоту\(\omega\), до числа кутових хвиль\(k\);
    5. Розв'язувати задачі примусових коливань за допомогою граничних умов;
    6. Проаналізуйте інваріантні системи космічного перекладу зв'язаних\(LC\) ланцюгів.

    Проблеми

    5.1. Розглянемо малі поздовжні коливання системи, наведені нижче:

    clipboard_e9a25279507dab24a62d972e41a14895a.png

    На малюнку вище кожен боб має масу\(m\), кожен маятник має довжину\(\ell\), кожна пружина має постійну пружину\(\kappa\), а рівноважний поділ між бобами є\(a\).

    1. Знайти\(M^{-1}K\) матрицю для цієї системи в основі, в якій зміщення блоків від рівноваги вимірюються вправо і розташовані в вектор очевидним чином,\ [X (t) =\ left (\ begin {array} {l}
      x_ {1} (t)\\
      x_ {2} (t)\\
      x_ {3} (t)\\
      x_ {4} (t)
      \ end {масив}\ справа).\]
    2. Класифікуйте як TRUE або FALSE кожне з наступних питань щодо нормальних режимів цієї системи. Якщо можливо, поясніть свої відповіді якісно, тобто словами, а не шляхом підключення до формули, і обговоріть загальність ваших результатів.
      1. У звичайному режимі з найменшою частотою все блоки рухаються в одному напрямку, коли вони взагалі рухаються.
      2. У звичайному режимі з другою найнижчою частотою 1-й і 2-й блоки мають однакове зміщення.
      3. У звичайному режимі з найбільшою частотою сусідні блоки рухаються в протилежних напрямках, коли вони взагалі рухаються.
    3. Знайдіть кутові частоти кожного з нормальних режимів. Підказка: Ви можете використовувати співвідношення дисперсії для зв'язаних маятників,\[\omega^{2}=2 B-2 C \cos k a\]

    де\[B=\frac{g}{2 \ell}+\frac{\kappa}{m}, \quad C=\frac{\kappa}{m} .\]

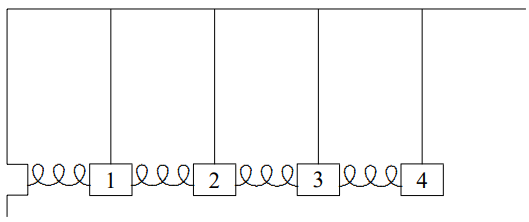
    5.2.

    clipboard_e89d3d32a981332605cb08261f797964b.png

    У наведеній вище системі всі блоки мають масу m і вони обмежені переміщатися тільки по горизонталі. Довгі пружини з шістьма петлями мають постійну пружину\(K\). Більш короткі пружини, з трьома петлями, мають постійну пружину\(2K\). Найкоротші пружини, з двома петлями, мають постійну пружину\(3K\). Як ви побачите в розділі 7, це те, що ми очікуємо, якщо пружини всі зроблені з одного матеріалу (див. Малюнок\( 7.1\)). Знайдіть нормальні режими роботи системи і відповідні частоти. Переконайтеся, що ви виправдовуєте будь-які припущення, які ви робите щодо звичайних режимів. Підказка: Спробуйте знайти нескінченну систему з інваріантністю перекладу простору, яка містить це таким чином, що ви можете поставити фізику стін як граничну умову. Ще одна підказка: Це працює просто, лише якщо три петлеві пружини мають рівно вдвічі більшу постійну пружини довгих пружин. Ваша відповідь повинна пояснити, чому.

    5.3. У бісерної нитки, показаної нижче, інтервал між сусідніми намистинами дорівнює\(a\), а відстань від торцевих намистин до стін -\(a / 2\). Всі намистини мають масу\(m\) і обмежені рухатися тільки вертикально, в площині паперу.

    clipboard_e9205720537722eafbf7b8c55cf5dc9b1.png

    Покажіть, що фізика лівої стіни може бути включена, перейшовши до нескінченної системи і вимагаючи граничної умови\(A_{0} = -A_{1}\).

    1. Легко. Знайдіть аналогічну граничну умову для правої стінки.
    2. Знайдіть нормальні режими і відповідні частоти.

    5.4. Розглянемо наступну схему:

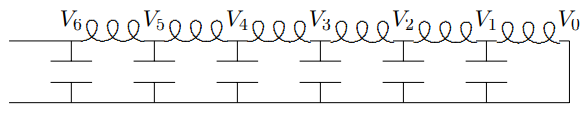
    clipboard_e0dd5eab05e0daecf6285648e663eac6e.png

    Всі конденсатори мають однакову ємність\(C \approx 0.00667 \mu F\), і всі індуктори мають однакову індуктивність,\(L \approx 150 \mu H\) і немає опору. Центральний провід заземлений. Ця схема є електричним аналогом інваріантних систем космічного перекладу зв'язаних механічних осциляторів, про які ми говорили в цьому розділі.

    Коли ви подаєте гармонічно коливальний сигнал від генератора сигналів через коаксіальний кабель до\(V_{6}\), різні коливальні напруги будуть індуковані вздовж лінії. Тобто, якщо\[V_{6}(t)=V \cos \omega t ,\]

    то\(V_{j}(t)\) має вигляд\[V_{j}(t)=A_{j} \cos \omega t+B_{j} \sin \omega t .\]

    Знайти\(A_{j}\) і\(B_{j}\).