Loading [MathJax]/jax/element/mml/optable/GreekAndCoptic.js
Skip to main content
LibreTexts - Ukrayinska

15.3: Періодичний рух

  2. Last updated
    Oct 27, 2022
  3. Save as PDF

  • Boundless
  • Boundless

навчальні цілі

  • Практика перетворення між частотою і періодом

Період і періодичність

Звичайна фізична термінологія руху, що повторюється знову і знову, - це періодичний рух, а час, необхідний для одного повторення, називається періодом, часто виражається у вигляді букви Т. (Символ Р не використовується через можливу плутанину з імпульсом.) Одне повне повторення руху називається циклом. Частота визначається як кількість циклів за одиницю часу. Частота зазвичай позначається латинською літерою f або грецької буквою ν (nu). Зверніть увагу, що період і частота є взаємними один одному.

зображення

Синусоїдальні хвилі різних частот: синусоїдальні хвилі різних частот; нижні хвилі мають вищі частоти, ніж ті, що наведені вище. Горизонтальна вісь представляє час.

f=1T

Наприклад, якщо серце новонародженої дитини б'ється з частотою 120 разів на хвилину, його період (інтервал між ударами) становить півсекунди. Якщо ви калібруєте свою інтуїцію так, що очікуєте, що великі частоти будуть поєднані з короткими періодами, і навпаки, ви можете уникнути деяких незручних помилок на іспитах з фізики.

Одиниці

зображення

Колеса локомотива: Колеса локомотива обертаються з частотою f циклів в секунду, що також можна описати як ω радіани в секунду. Механічні зв'язки дозволяють лінійної вібрації поршнів парового двигуна, на частоті f, приводити в рух колеса.

В одиницях СІ одиницею частоти є герц (Гц), названий на честь німецького фізика Генріха Герца: 1 Гц вказує на те, що подія повторюється раз в секунду. Традиційною одиницею виміру, що використовується з обертовими механічними пристроями, є обороти в хвилину, скорочено RPM. 60 об/хв дорівнює одному герцу (тобто одному обороту в секунду, або періоду в одну секунду). Одиниця СІ за період - друга.

Кутова частота

Часто періодичний рух найкраще виражається через кутову частоту, представлену грецькою буквою ω (омега). Кутова частота відноситься до кутового зміщення в одиницю часу (наприклад, при обертанні) або швидкості зміни фази синусоїдальної форми хвилі (наприклад, в коливаннях і хвиль), або як швидкість зміни аргументу синусоїдальної функції.

\mathrm{y(t)= \sin (θ(t))= \sin (ωt)= \sin (2πft)}

\mathrm{ω=2πf}

Кутова частота часто представлена в одиницях радіанів в секунду (нагадаємо, є 2π радіани по колу).

Період меси на весні

Період маси m на пружині пружини постійної k можна обчислити як\mathrm{T=2π \sqrt{\frac{m}{k}}}.

навчальні цілі

  • Визначити параметри, необхідні для розрахунку періоду і частоти коливальної маси на кінець ідеальної пружини

Розуміння відновлювальної сили

Перший закон Ньютона передбачає, що об'єкт, що коливається вперед і назад, відчуває сили. Без сили об'єкт рухався по прямій лінії з постійною швидкістю, а не коливатися. Важливо розуміти, як сила на об'єкт залежить від положення об'єкта. Якщо предмет вібрує вправо і вліво, то він повинен мати ліву силу на ньому, коли він знаходиться з правого боку, і праву силу, коли він знаходиться з лівого боку. В одному вимірі ми можемо представляти напрямок сили, використовуючи позитивний або негативний знак, і оскільки сила змінюється від позитивної до негативної, в середині повинна бути точка, де сила дорівнює нулю. Це точка рівноваги, де об'єкт залишався б у спокої, якби його відпустили в спокої. Загальною умовою є визначення походження нашої системи координат так, що х дорівнює нулю при рівновазі.

зображення

Коливальна лінійка: При зміщенні з положення вертикальної рівноваги ця пластикова лінійка коливається вперед і назад через відновлювальну силу, протилежну зміщенню. Коли лінійка знаходиться зліва, є сила вправо, і навпаки.

Розглянемо, наприклад, вищипування пластикової лінійки, зображеної на першому малюнку. Деформація лінійки створює силу в зворотному напрямку, відому як відновлювальна сила. Після звільнення відновлювальна сила змушує лінійку рухатися назад до свого стабільного положення рівноваги, де чиста сила на ній дорівнює нулю. Однак до того моменту, як лінійка туди потрапляє, вона набирає обертів і продовжує рухатися вправо, виробляючи протилежну деформацію. Потім він змушений вліво, назад через рівновагу, і процес повторюється до тих пір, поки дисипативні сили (наприклад, тертя) не послаблять рух. Ці сили видаляють механічну енергію з системи, поступово зменшуючи рух, поки лінійка не прийде в спокій.

зображення

Відновлення сили, імпульсу та рівноваги: (а) Пластикова лінійка була звільнена, і відновлююча сила повертає лінійку в положення рівноваги. (b) Чиста сила дорівнює нулю в положенні рівноваги, але лінійка має імпульс і продовжує рухатися вправо. (c) Відновлююча сила знаходиться в зворотному напрямку. Він зупиняє лінійку і знову переміщує її до рівноваги. (г) Тепер лінійка має імпульс ліворуч. (е) При відсутності демпфування (викликаного силами тертя) лінійка досягає вихідного положення. Звідти рух повториться.

Закон Гука

Найпростіші коливання виникають, коли відновлююча сила прямо пропорційна зміщенню. Назва, яка була дана цій залежності між силою і зміщенням, - закон Гука:

\mathrm{F=kx}

Тут F - відновлювальна сила, х - зміщення від рівноваги або деформації, а k - константа, пов'язана з труднощами деформування системи (часто називають постійною пружини або постійною сили). Пам'ятайте, що знак мінус вказує на те, що відновлює зусилля знаходиться в напрямку, протилежному зміщенню. Константа сили k пов'язана з жорсткістю (або жорсткістю) системи - чим більша сила постійна, тим більша сила відновлення, і тим жорсткіша система. Одиниці k - ньютони на метр (Н/м). Наприклад, k безпосередньо пов'язаний з модулем Юнга, коли ми розтягуємо рядок. Типовим фізичним лабораторним вправою є вимірювання відновлювальних сил, створених пружинами, визначення, чи дотримуються вони закону Гука, і обчислити їх силові константи, якщо вони це роблять.

Маса на пружині

Поширеним прикладом заперечення, що коливається назад і вперед відповідно до відновлювальної сили, прямо пропорційної зміщенню від рівноваги (тобто, слідуючи Закону Гука), є випадок маси на кінці ідеальної пружини, де «ідеал» означає, що ніякі брудні реальні змінні не заважають уявний результат.

Рух маси на пружині можна охарактеризувати як Простий гармонічний рух (SHM), назва коливального руху для системи, де чиста сила може бути описана законом Гука. Тепер ми можемо визначити, як розрахувати період і частоту коливається маси на кінець ідеальної пружини. Період Т можна обчислити, знаючи тільки масу, м, і постійну сили, k:

\mathrm{T=2π\sqrt{\frac{m}{k}}}

При роботі з\mathrm{f=\frac{1}{T}} частотою задаються:

\mathrm{f=\frac{1}{2π} \sqrt{\frac{k}{m}}}

Ми можемо зрозуміти залежність цих рівнянь від m і k інтуїтивно. Якщо збільшити масу на коливальній пружинній системі з заданим k, збільшена маса забезпечить більшу інерцію, викликаючи зменшення прискорення за рахунок відновлювальної сили F (нагадаємо Другий закон Ньютона:\mathrm{F=ma}). Це дозволить подовжити період коливань і зменшити частоту. На відміну від цього, збільшення постійної сили k збільшить відновлювальну силу відповідно до Закону Гука, в свою чергу, спричиняючи збільшення прискорення в кожній точці переміщення. Це скорочує термін і збільшує частоту. Максимальний зміщення від рівноваги відомий як амплітуда X.

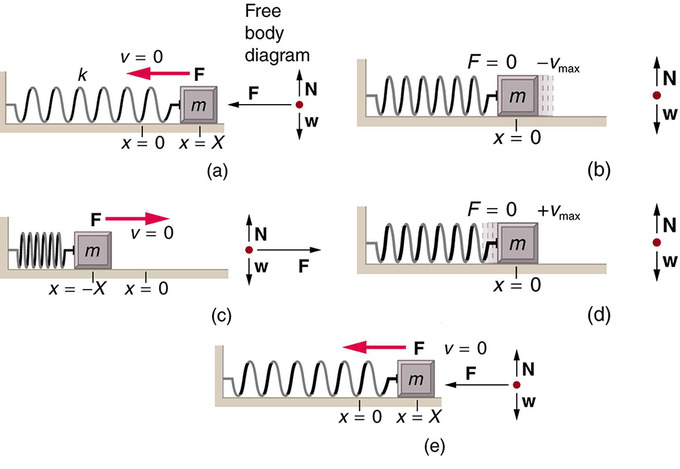
зображення

Рух маси на ідеальній пружині: Об'єкт, прикріплений до пружини, що ковзає по поверхні без тертя, є нескладним простим гармонічним осцилятором. При зміщенні з рівноваги об'єкт виконує простий гармонічний рух, який має амплітуду X і період T Максимальна швидкість об'єкта відбувається при проходженні через рівновагу. Чим жорсткіше пружина, тим менше період Т. Чим більше маса предмета, тим більше період Т. (а) Маса досягла свого найбільшого зміщення X вправо і тепер відновлювальна сила вліво знаходиться на максимальній величині. (b) Відновлювальна сила перемістила масу назад до точки рівноваги і тепер дорівнює нулю, але швидкість вліво знаходиться на максимумі. (c) Імпульс маси переніс її до максимального зміщення вправо. Відновлююча сила тепер праворуч, рівна за величиною і протилежна за напрямком порівняно з (а). (d) Точка рівноваги знову досягається, цього разу з імпульсом вправо. (е) Цикл повторюється.

Простий гармонійний рух

Простий гармонійний рух - це тип періодичного руху, де відновлювальна сила прямо пропорційна зміщенню.

навчальні цілі

  • Пов'язати відновлювальну силу і зміщення під час простого гармонічного руху

Простий гармонійний рух

Простий гармонічний рух - це тип періодичного руху, де відновлювальна сила прямо пропорційна зміщенню (тобто вона слідує закону Гука). Він може служити математичною моделлю різноманітних рухів, таких як коливання пружини. Крім того, інші явища можуть бути наближені простим гармонійним рухом, таким як рух простого маятника, або молекулярна вібрація.

Простий гармонійний рух: Короткий вступ до простого гармонічного руху для студентів фізики на основі обчислень.

Простий гармонічний рух характеризується рухом маси на пружині, коли вона піддається лінійній пружній відновлювальній силі, заданої Законом Гука. Система, яка слідує простим гармонійним рухом, відома як простий гармонійний генератор.

Динаміка простих гармонічних коливань

Для одновимірного простого гармонічного руху рівняння руху (яке є лінійним звичайним диференціальним рівнянням другого порядку з постійними коефіцієнтами) можна отримати за допомогою другого закону Ньютона і закону Гука.

\mathrm{F_{net}=m\dfrac{d^2x}{dt^2}=−kx,}

де m - маса тіла, що коливається, x - його зміщення з положення рівноваги, а k - постійна пружини. Тому:

\mathrm{\dfrac{d^2x}{dt^2}=−(\dfrac{k}{m})x.}

Вирішуючи диференціальне рівняння вище, отримано рішення, яке є синусоїдальною функцією.

\mathrm{x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)=A \cos (ωt−φ),}

де

\mathrm{ω=\sqrt{\dfrac{k}{m}},}

\mathrm{A=\sqrt{c_1^2+c_2^2},}

\mathrm{\tan φ=(\dfrac{c_2}{c_1}).}

У розчині c 1 і c 2 - це дві константи, що визначаються початковими умовами, а початок встановлюється в положення рівноваги. Кожна з цих констант несе фізичний сенс руху: A - амплітуда (максимальне зміщення з положення рівноваги),\mathrm{ω = 2πf} - кутова частота, а φ - фаза.

Ми можемо використовувати диференціальне числення і знайти швидкість і прискорення як функцію часу:

\mathrm{v(t)=\dfrac{dx}{dt}=−Aω \sin (ωt−φ)}

\mathrm{a(t)=\dfrac{d^2x}{dt^2}=−Aω^2 \cos (ωt−φ).}

Прискорення також може виражатися у вигляді функції переміщення:

\mathrm{a(t)=−ω^2x.}

Тоді з тих пір\mathrm{ω = 2πf},

\mathrm{f=\dfrac{1}{2π}\sqrt{\dfrac{k}{m}}.}

Нагадуючи, що\mathrm{T=\frac{1}{f}},

\mathrm{T=2π \sqrt{\dfrac{m}{k}}.}

Використовуючи Другий закон Ньютона, Закон Гука та деяке диференціальне числення, ми змогли вивести період і частоту маси, що коливається на пружині, з якою ми зіткнулися в останньому розділі! Відзначимо, що період і частота повністю не залежать від амплітуди.

На малюнку нижче показано простий гармонічний рух об'єкта на пружині та представлені графіки x (t), v (t) та a (t) проти часу. Ви повинні навчитися створювати розумові зв'язки між вищезазначеними рівняннями, різними положеннями об'єкта на пружині в мультфільмі та пов'язаними позиціями на графіках x (t), v (t) та a (t).

зображення

Візуалізація простого гармонічного руху: графіки x (t), v (t) та a (t) проти t для руху об'єкта на пружині. Чиста сила на об'єкті може бути описана законом Гука, і тому об'єкт піддається простому гармонійному руху. Зверніть увагу, що початкове положення має вертикальне зміщення при максимальному значенні X; v спочатку дорівнює нулю, а потім негативному, коли об'єкт рухається вниз; і початкове прискорення негативне, назад до положення рівноваги і стає нулем у цій точці.

Простий гармонійний рух і рівномірний круговий рух

Просте гармонійне рух виробляється проекцією рівномірного кругового руху на одну з осей в площині xy.

навчальні цілі

  • Опишіть зв'язок між простим гармонічним рухом і рівномірним круговим рухом

Рівномірний круговий рух

Рівномірний круговий рух описує рух тіла, що проходить по круговому шляху з постійною швидкістю. Відстань тіла від центру кола залишається постійним у всі часи. Хоча швидкість тіла постійна, його швидкість не є постійною: швидкість (векторна величина) залежить як від швидкості тіла, так і від напрямку руху. Оскільки тіло постійно змінює напрямок, коли воно рухається по колу, швидкість також змінюється. Ця різна швидкість вказує на наявність прискорення, званого доцентровим прискоренням. Доцентрове прискорення має постійну величину і спрямоване в усі часи до центру кола. Це прискорення, в свою чергу, виробляється доцентровою силою - силою постійної величини і спрямованою до центру.

Швидкість

Наведений вище малюнок ілюструє вектори швидкості і прискорення для рівномірного руху в чотирьох різних точках орбіти. Оскільки швидкість v дотична до кругового шляху, жодна дві швидкості не вказують в одному напрямку. Хоча об'єкт має постійну швидкість, напрямок його завжди змінюється. Ця зміна швидкості обумовлена прискоренням, а, величина якого (як і швидкість) утримується постійною, але напрямок якого також завжди змінюється. Прискорення вказує радіально всередину (доцентрово) і перпендикулярно швидкості. Це прискорення відоме як доцентрове прискорення.

зображення

Рівномірний круговий рух (у чотирьох різних точках орбіти): швидкість v і прискорення a в рівномірному круговому русі з кутовою швидкістю ω; швидкість постійна, але швидкість завжди дотична до орбіти; прискорення має постійну величину, але завжди вказує на центр обертання

Зсув навколо кругової траєкторії часто задається через кут θ. Цей кут являє собою кут між прямою лінією, проведеною від центру кола до початкового положення об'єктів на краю, і прямою лінією, проведеною від кінцевого положення об'єктів від краю до центру кола. Див. Наочне зображення кута, де точка p почалася на осі x- і перемістилася в поточне положення. Кут θ описує, як далеко він перемістився.

зображення

Проекція рівномірного кругового руху: точка P, що рухається по круговому шляху з постійною кутовою швидкістю ω, зазнає рівномірного кругового руху. Його проекція на вісь х піддається простому гармонійному руху. Також показана швидкість цієї точки навколо кола v−max та її проекція, яка є v. Зверніть увагу, що ці швидкості утворюють подібний трикутник до трикутника зміщення.

Для шляху навколо кола радіусом r, коли кут θ (вимірюється в радіанах) змітається, відстань, пройдена по краю кола, дорівнює s = rθ. Ви можете довести це самостійно, пам'ятаючи, що окружність кола є\mathrm{2 \pi r}, тому, якщо об'єкт подорожував по всьому колу (одній окружності), він пройшов кут\mathrm{2 \pi} радіанів і пройшов відстань\mathrm{2 \pi r}. Тому швидкість пересування по орбіті становить:

\mathrm{v=r\dfrac{dθ}{dt}=rω,}

де кутова швидкість обертання дорівнює ω. (Зауважте, що\mathrm{ω = \frac{v}{r}}.) Таким чином, v - константа, а вектор швидкості v також обертається з постійною величиною v, з тією ж кутовою швидкістю ω.

Прискорення

Прискорення при рівномірному круговому русі завжди спрямоване всередину і задається:

\mathrm{a=v\dfrac{dθ}{dt}=vω=\dfrac{v^2}{r}.}

Це прискорення діє на зміну напрямку v, але не швидкості.

Простий гармонійний рух від рівномірного кругового руху

Існує простий спосіб зробити простий гармонічний рух за допомогою рівномірного кругового руху. На малюнку нижче демонструється один із способів використання цього методу. Куля кріпиться до рівномірно обертається вертикального поворотного столу, а його тінь проектується на підлогу, як показано на малюнку. Тінь піддається простому гармонійному руху.

зображення

Тінь кулі, що переживає простий гармонійний рух: Тінь кулі, що обертається з постійною кутовою швидкістю ω на поворотному столі, йде вперед і назад у точному простому гармонійному русі.

На наступному малюнку показана основна залежність між рівномірним круговим рухом і простим гармонійним рухом. Точка Р рухається по колу з постійною кутовою швидкістю ω. Точка Р аналогічна кулі на поворотній платці на малюнку вище. Проекція положення Р на нерухому вісь піддається простому гармонійному руху і аналогічна тіні об'єкта. У певний момент часу, прийнятий на малюнку, проекція має положення x і рухається вліво зі швидкістю v. Швидкість точки Р навколо кола дорівнює |v max |. Проекція |v max | на вісь x - це швидкість v простого гармонічного руху вздовж осі x.

Щоб побачити, що проекція зазнає простий гармонійний рух, зверніть увагу, що її положення x задається:

\mathrm{x=X \cos θ,}

де θ = ωt, ω - постійна кутова швидкість, а X - радіус кругового шляху. Таким чином,

\mathrm{x=X \cos ωt.}

Кутова швидкість ω знаходиться в радіанах за одиницю часу; в цьому випадку 2π радіани - це час для одного обороту T. Тобто,\mathrm{ω=\frac{2π}{T}}. Підставивши це вираз на ω, ми бачимо, що позиція x задається:

\mathrm{x(t)= \cos (\dfrac{2πt}{T})=\cos (2πft).}

Примітка: Це рівняння має виглядати знайомим з нашого попереднього обговорення простого гармонічного руху.

Простий маятник

Простий маятник діє як гармонійний осцилятор з періодом, залежним тільки від L і g для досить малих амплітуд.

навчальні цілі

  • Визначте параметри, що впливають на період простого маятника

Простий маятник

Маятник - це вага, підвішений на шарнірі, щоб він міг вільно розгойдуватися. Коли маятник зміщується вбік від положення рівноваги спокою, він піддається відновлювальній силі; після того, як він досягне найвищої точки в своєму розгойдуванні, гравітація прискорить його назад до положення рівноваги. При звільненні відновлювальна сила в поєднанні з масою маятника змушує його коливатися навколо положення рівноваги, розгойдуючись вперед-назад.

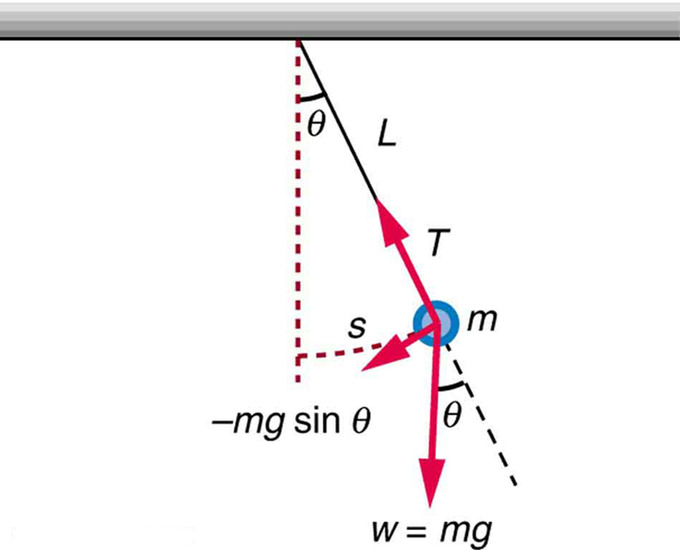
зображення

Простий маятник: Простий маятник має боб малого діаметра і струну, яка має дуже малу масу, але досить міцна, щоб не розтягнутися помітно. Лінійне зміщення від рівноваги - s, довжина дуги. Також показані сили на боб, які призводять до чистої сили −mgsinθ до положення рівноваги - тобто відновлювальної сили.

Для невеликих переміщень маятник є простим гармонічним осцилятором. Простий маятник визначається як предмет, який має невелику масу, також відомий як маятниковий боб, який підвішений на дроті або нитці незначної маси, як показано на ілюструючому малюнку. Досліджуючи простий маятник трохи далі, ми можемо виявити умови, за яких він виконує простий гармонійний рух, і ми можемо вивести цікавий вираз для його періоду.

Маятники: Короткий вступ до маятників (як ідеальних, так і фізичних) для студентів фізики на основі обчислень з точки зору простого гармонічного руху.

Почнемо з визначення зміщення, щоб бути довжиною дуги s. З малюнка бачимо, що чиста сила на бобі дотична до дуги і дорівнює − mg sin θ. (Вага mg має компоненти mg cos θ уздовж струни і mg sin θ дотичною до дуги.) Напруга в струні точно скасовує компонент mg cos θ паралельно струні. Це залишає чисту відновлювальну силу, яка тягне маятник назад до положення рівноваги при θ = 0.

Тепер, якщо ми можемо показати, що відновлювальна сила прямо пропорційна зміщенню, то у нас є простий гармонічний генератор. Намагаючись визначити, чи є у нас простий гармонічний генератор, слід зазначити, що для малих кутів (менше приблизно 15º), sin θ ≈ θ (sin θ і θ відрізняються приблизно на 1% або менше під меншими кутами). Таким чином, для кутів менше приблизно 15º відновлююча сила F дорівнює

\mathrm{F≈−mgθ.}

Зсув s прямо пропорційно θ. Коли θ виражається в радіанах, довжина дуги в колі пов'язана з її радіусом (L в даному випадку):

S = Lθ = Lθ

щоб

\mathrm{θ=sL.}

Тоді для малих кутів вираз для відновлювальної сили є:

\mathrm{F≈\dfrac{mgL}{s}.}

Цей вислів має форму закону Гука:

\mathrm{F≈−kx}

де константа сили задана k = mg/ L, а зміщення задається x = s. Для кутів менше приблизно 15º відновлювальна сила прямо пропорційна зміщенню, а простий маятник є простим гармонічним осцилятором.

Використовуючи це рівняння, ми можемо знайти період маятника для амплітуд менше приблизно 15º. Для простого маятника:

\mathrm{T=2π\sqrt{\dfrac{m}{k}}=2π\sqrt{\dfrac{m}{\dfrac{mg}{L}}}.}

Таким чином,

\mathrm{T=2π\sqrt{\dfrac{L}{g}}}

або період простого маятника. Такий результат цікавий своєю простотою. Єдине, що впливає на період простого маятника - це його довжина і прискорення за рахунок сили тяжіння. Період повністю не залежить від інших факторів, таких як маса. Навіть прості маятникові годинники можуть бути тонко відрегульовані та точні. Відзначимо залежність Т від г. Якщо довжина маятника точно відома, його насправді можна використовувати для вимірювання прискорення за рахунок сили тяжіння. Якщо θ менше приблизно 15º, період T для маятника майже не залежить від амплітуди, як у простих гармонічних осциляторів. При цьому рух маятника в залежності від часу можна змоделювати як:

\mathrm{θ(t)=θ_o \cos (\dfrac{2πt}{T})}

Для амплітуд, більших за 15º, період поступово збільшується з амплітудою, тому він довший, ніж дано простим рівнянням для T вище. Наприклад, при амплітуді θ 0 = 23° вона на 1% більше. Період збільшується асимптотично (до нескінченності), коли θ 0 наближається до 180°, оскільки значення θ 0 = 180° є нестійкою точкою рівноваги для маятника.

Фізичний маятник

Період фізичного маятника залежить від моменту його інерції щодо точки повороту та відстані від центру мас.

навчальні цілі

  • Визначте параметри, що впливають на період фізичного маятника

Фізичний маятник

Нагадаємо, що простий маятник складається з маси, підвішеної до безмасової струни або стрижня на нефрикційному шарнірі. В такому випадку ми можемо знехтувати будь-яким ефектом від самої струни або стрижня. На відміну від цього, фізичний маятник (іноді його називають складовим маятником) може бути підвішений стрижнем, який не є безмасовим або, більш загалом, може бути довільної форми, жорстке тіло, що гойдається за допомогою шарніра (див.). При цьому період маятника залежить від моменту його інерції навколо точки повороту.

Маятники - Фізичний маятник: Короткий вступ до маятників (як ідеальних, так і фізичних) для студентів фізики на основі обчислень з точки зору простого гармонічного руху.

зображення

Фізичний маятник: приклад, що показує, як сили діють через центр маси. Ми можемо обчислити період цього маятника, визначивши момент інерції об'єкта навколо точки повороту.

Гравітація діє через центр мас твердого тіла. Значить, довжина маятника, використовуваного в рівняннях, дорівнює лінійному відстані між шарніром і центром мас (h).

Рівняння крутного моменту дає:

\mathrm{τ=Iα,}

де α - кутове прискорення, τ - крутний момент, а I - момент інерції.

Крутний момент генерується самопливом так:

\mathrm{τ=mgh \sin θ,}

де h - відстань від центру мас до точки повороту і θ - кут від вертикалі.

Отже, під малокутовим наближенням sin\ theta\ prox\ theta,

\mathrm{α≈−\dfrac{mghθ}{I}.}

Це тієї ж форми, що і звичайний простий маятник, і це дає період:

\mathrm{T=2π\sqrt{\dfrac{I}{mgh}}.}

І частота:

\mathrm{f=\dfrac{1]{T}=\dfrac{1}{2π}\sqrt{\dfrac{mgh}{I}}.}

У разі, якщо нам відомий момент інерції жорсткого тіла, ми можемо оцінити вищевказаний вираз періоду для фізичного маятника. Для ілюстрації розглянемо рівномірний жорсткий стрижень, відкинутий від рами, як показано на малюнку (див.). Зрозуміло, що центр мас знаходиться на відстані L/2 від точки підвісу:

зображення

Рівномірний жорсткий стрижень: Жорсткий стрижень з рівномірним розподілом маси висить з точки повороту. Це ще один приклад фізичного маятника.

\mathrm{h=\dfrac{L}{2}.}

Момент інерції жорсткого стрижня про його центр дорівнює:

\mathrm{I_c=\dfrac{mL^2}{12}.}

Однак нам потрібно оцінити момент інерції щодо точки повороту, а не центру мас, тому застосуємо теорему паралельної осі:

\mathrm{I_o=I_c+mh^2=\dfrac{mL^2}{12}+m(\dfrac{L}{2})^2=\dfrac{mL^2}{3}.}

Включивши цей результат в рівняння для періоду, ми маємо:

\mathrm{T=2π\sqrt{\dfrac{I}{mgh}}=2π\sqrt{\dfrac{2mL^2}{3mgL}}=2π\sqrt{\dfrac{2L}{3g}}.}

Важливо відзначити про це відношення, що період все ще не залежить від маси жорсткого тіла. Однак він не є незалежним від масового розподілу жорсткого тіла. Зміна форми, розміру або розподілу маси змінить момент інерції. Це, в свою чергу, змінить період.

Як і у випадку з простим маятником, фізичний маятник можна використовувати для вимірювання g.

Енергія в простому гармонічному осциляторі

Загальна енергія в простому гармонічному осциляторі - це постійна сума потенційної та кінетичної енергій.

навчальні цілі

  • Поясніть, чому загальна енергія гармонічного генератора постійна

Енергія в простому гармонічному осциляторі

Для вивчення енергії простого гармонічного осцилятора спочатку розглянемо всі форми енергії, які він може мати. Нагадаємо, що потенційна енергія (ПЕ), що зберігається навесні, що слідує Закону Гука, є:

\mathrm{PE=\dfrac{1}{2}kx^2,}

де ПЕ - потенційна енергія, k - постійна пружини, а x - величина зміщення або деформації. Оскільки простий гармонічний генератор не має дисипативних сил, іншою важливою формою енергії є кінетична енергія (KE). Збереження енергії для цих двох форм - це:

\mathrm{KE+PE=constant,}

які можуть бути записані як:

\mathrm{\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2=constant.}

Це твердження збереження енергії справедливо для всіх простих гармонійних осциляторів, в тому числі і тих, де гравітаційна сила грає певну роль. Наприклад, для простого маятника замінимо швидкість на v = Lω, постійну пружини з k = mg/L, а термін зміщення на x = Lθ. Таким чином:

\mathrm{\dfrac{1}{2}mL^2ω^2+\dfrac{1}{2}mgLθ^2=constant.}

У разі незгасаного, простого гармонійного руху енергія коливається взад-вперед між кінетичним і потенційним, повністю переходячи від одного до іншого, коли система коливається. Отже, для простого прикладу об'єкта на поверхні без тертя, прикріпленої до пружини, як показано знову (див.), рух починається з усієї енергії, що зберігається навесні. Коли об'єкт починає рухатися, пружна потенційна енергія перетворюється в кінетичну енергію, стаючи цілком кінетичною енергією в положенні рівноваги. Потім він перетворюється назад в пружну потенційну енергію пружиною, швидкість стає нульовою, коли кінетична енергія повністю перетворюється, і так далі. Ця концепція забезпечує додаткове розуміння тут і в пізніших додатках простого гармонічного руху, таких як ланцюги змінного струму.

зображення

Енергія в простому гармонічному осциляторі: Перетворення енергії в простому гармонічному русі ілюстровано для об'єкта, прикріпленого до пружини на поверхні без тертя. (а) Маса досягла максимального зміщення від рівноваги. Вся енергія є потенційною енергією. (b) Коли маса проходить через точку рівноваги з максимальною швидкістю, вся енергія в системі знаходиться в кінетичній енергії. (в) Ще раз вся енергія знаходиться в потенційній формі, що зберігається при стисненні пружини (в першій панелі енергія зберігалася в продовженні пружини). (d) Проходячи через рівновагу знову вся енергія є кінетичною. (е) Маса завершила цілий цикл.

Принцип збереження енергії може бути використаний для отримання виразу для швидкості v. Якщо ми розпочнемо наш простий гармонічний рух з нульовою швидкістю та максимальним зміщенням (x = X), то загальна енергія дорівнює:

\mathrm{E=\dfrac{1}{2}kX^2.}

Ця загальна енергія є постійною і зміщується взад-вперед між кінетичною енергією та потенційною енергією, в більшості випадків ділиться кожним. Збереження енергії для цієї системи у вигляді рівняння, таким чином:

\mathrm{\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2=\dfrac{1}{2}kX^2.}

Розв'язування цього рівняння для v дає:

\mathrm{v=±\sqrt{\dfrac{k}{m}(X^2−x^2).}}

Маніпулювання цим виразом алгебраїчно дає:

\mathrm{v=±\sqrt{\dfrac{k}{m}}X\sqrt{1−\dfrac{x^2}{X^2}},}

і так:

\mathrm{v=±v_{max}\sqrt{1−\dfrac{x^2}{X^2}},}

де:

\mathrm{v_{max}=\sqrt{\dfrac{k}{m}}X.}

З цього виразу ми бачимо, що швидкість максимальна (v max) при x =0. Зверніть увагу, що максимальна швидкість залежить від трьох факторів. Вона прямо пропорційна амплітуді. Як неважко здогадатися, чим більше максимальне переміщення, тим більше максимальна швидкість. Це також більше для жорсткіших систем, оскільки вони надають більшу силу для того ж переміщення. Це спостереження видно у виразі для v max; воно пропорційно квадратному кореню постійної сили k. Нарешті, максимальна швидкість менше для об'єктів, що мають більші маси, тому що максимальна швидкість обернено пропорційна квадратному кореню m. При заданій силі предмети, що мають великі маси, прискорюються повільніше.

Подібний розрахунок для простого маятника дає аналогічний результат, а саме:

\mathrm{ω_{max}=\sqrt{\dfrac{g}{L}}θ_{max}.}

Досвід роботи з простим гармонічним осцилятором: відома маса підвішується з пружини відомої постійної пружини і дозволяє коливатися. Вимірюється час одного коливання (періоду). Ця величина порівнюється з прогнозованою величиною, виходячи з маси і постійної пружини.

Синусоїдальна природа простого гармонічного руху

Розв'язки рівнянь руху простих гармонічних осциляторів завжди синусоїдальні, тобто синуси і косинуси.

навчальні цілі

  • Огляд факторів, що відповідають за синусоїдальну поведінку рівномірного кругового руху

Синусоїдальна природа простого гармонічного руху

Чому синусоїди так поширені?

Якби система маси -на-пружині, розглянута в попередніх розділах, повинна була бути побудована, а її рух вимірювався точно, її графік x - t був би майже ідеальною синусоїдальною формою, як показано на. Його називають «синусоїдальною» або «синусоїдальною», навіть якщо це косинус, або синус або косинус, зміщений на якусь довільну горизонтальну величину. Можливо, не дивно, що це похитування такого загального роду, але чому це конкретна математично ідеальна форма? Чому це не пилкоподібна форма, як у (2); або якась інша форма, як у (3)? Примітно, що величезна кількість, очевидно, не пов'язаних між собою вібраційних систем, демонструють однакову математичну особливість. Камертон, відтягнутий в одну сторону і відпущений саджанець, автомобіль підстрибує на своїх амортизаторах, всі ці системи будуть проявляти синусоїдальний рух за однієї умови: амплітуда руху повинна бути невеликою.

зображення

Синусоїдальні та несинусоїдальні коливання: Тільки верхній графік є синусоїдальним. Інші змінюються з постійною амплітудою та періодом, але не описують простий гармонійний рух.

Закон Гука та генерація синусоїди

Ключ до розуміння того, як об'єкт вібрує, - це знати, як сила на об'єкт залежить від положення об'єкта. Якщо система дотримується Закону Гука, відновлювальна сила пропорційна зміщенню. Як торкалося в попередніх розділах, існує диференціальне рівняння другого порядку, яке стосується прискорення та переміщення.

\mathrm{F_{net}=m\dfrac{d^2x}{dt^2}=−kx.}

Коли це загальне рівняння вирішується для положення, швидкості і прискорення як функції часу:

  • \mathrm{x(t)=A \cos (ωt−φ)}
  • \mathrm{v(t)=\frac{dx}{dt}=−Aω \sin (ωt−φ)}
  • \mathrm{a(t)=\frac{d^2x}{dt^2}=−Aω^2 \cos (ωt−φ)}

Це все синусоїдальні розчини. Розглянемо масу на пружині, яка має маленьку ручку всередині біжить через рухому смужку паперу, коли вона відскакує, записуючи її рухи.

зображення

Маса на пружині, що виробляє синусоїду: Вертикальне положення об'єкта, що підстрибує на пружині, записується на смузі рухомого паперу, залишаючи синусоїду.

Наведені вище рівняння можуть бути переписані у формі, застосовній до змінних для маси на пружинній системі на малюнку.

  • \mathrm{x(t)=X \cos (\frac{2πt}{T})}
  • \mathrm{v(t)=−v_{max} \sin (\frac{2πt}{T})}
  • \mathrm{a(t)=−\frac{kX}{m} \cos (\frac{2πt}{T})}

Нагадаємо, що проекцію рівномірного кругового руху можна описати з точки зору простого гармонічного осцилятора. Рівномірний круговий рух, отже, також синусоїдальний, як ви можете бачити з.

зображення

Синусоїдальна природа рівномірного кругового руху: Положення проекції рівномірного кругового руху виконує простий гармонічний рух, як вказує цей хвилеподібний графік x проти t.

Миттєва енергія простого гармонічного руху

Рівняння, що обговорюються для складових загальної енергії простих гармонічних осциляторів, можуть бути об'єднані з синусоїдальними розв'язками для x (t), v (t) та a (t) для моделювання змін кінетичної та потенційної енергії в простому гармонічному русі.

Кінетична енергія K системи в момент t дорівнює:

\mathrm{K(t)=\dfrac{1}{2}mv^2(t)=\dfrac{1}{2}mω^2A^2 \sin ^2 (ωt−φ)=\dfrac{1}{2}kA^2 \sin ^2 (ωt−φ).}

Потенційна енергія U дорівнює:

\mathrm{U(t)=\dfrac{1}{2}kx^2(t)==\dfrac{1}{2}kA^2 \cos ^2(ωt−φ).}

Підсумовуючи K (t) і U (t) виробляється загальна механічна енергія, помічена раніше:

\mathrm{E=K+U=\dfrac{1}{2}kA^2.}

Ключові моменти

  • Рух, який повторюється регулярно, називається періодичним рухом. Одне повне повторення руху називається циклом. Тривалість кожного циклу - це період.
  • Частота відноситься до кількості циклів, виконаних за проміжок часу. Він є зворотним періодом і може бути обчислений за допомогою рівняння F = 1/t.
  • Деякий рух найкраще характеризується кутовою частотою (ω). Кутова частота відноситься до кутового зміщення в одиницю часу і розраховується з частоти з рівнянням\mathrm{ω=2πf}.
  • Якщо предмет вібрує вправо і вліво, то він повинен мати ліву силу на ньому, коли він знаходиться з правого боку, і праву силу, коли він знаходиться з лівого боку.
  • Відновлююча сила змушує коливальний об'єкт рухатися назад до свого стійкого положення рівноваги, де чиста сила на ньому дорівнює нулю.
  • Найпростіші коливання виникають, коли відновлююча сила прямо пропорційна зміщенню. При цьому силу можна обчислити як\mathrm{F=-kx}, де F - відновлювальна сила, k - постійна сили, а x - зміщення.
  • Рух маси на пружині можна охарактеризувати як Простий гармонічний рух (SHM): коливальний рух, що слідує закону Гука.
  • Період маси на пружині задається рівнянням\mathrm{T=2π\sqrt{\frac{m}{k}}}
  • Простий гармонічний рух часто моделюється на прикладі маси на пружині, де відновлювальна сила підпорядковується закону Гука і прямо пропорційна зміщенню об'єкта з його положення рівноваги.
  • Будь-яка система, яка підпорядковується простому гармонійному руху, відома як простий гармонійний генератор.
  • Рівняння руху, що описує простий гармонічний рух, можна отримати, об'єднавши Другий закон Ньютона і Закон Гука в лінійне звичайне диференціальне рівняння другого порядку:\mathrm{F_{net}=m\frac{d^2x}{dt^2}=−kx.}
  • Рівномірний круговий рух описує рух об'єкта, що рухається по круговому шляху з постійною швидкістю. Одновимірну проекцію цього руху можна охарактеризувати як простий гармонійний рух.
  • При рівномірному круговому русі вектор швидкості v завжди дотичний до кругового шляху і постійний за величиною. Прискорення постійне за величиною і вказує на центр кругового шляху, перпендикулярно вектору швидкості в кожну мить.
  • Якщо об'єкт рухається з кутовою швидкістю ω навколо кола радіуса r з центром у початку площини x-y, то його рух по кожній координаті є простим гармонічним рухом з амплітудою r і кутовою частотою ω.
  • Простий маятник визначається як об'єкт, який має невелику масу, також відомий як маятниковий боб, який підвішений на дроті або нитці незначної маси.
  • При зміщенні маятник буде коливатися навколо своєї точки рівноваги завдяки імпульсу в рівновазі з відновлювальною силою тяжіння.
  • Коли коливання (амплітуди) невеликі, менше приблизно 15º, маятник діє як простий гармонічний генератор з періодом\mathrm{T=2π\sqrt{\frac{L}{g}}}, де L - довжина струни, а g - прискорення за рахунок сили тяжіння.
  • Фізичний маятник - це узагальнений випадок простого маятника. Він складається з будь-якого твердого тіла, яке коливається навколо точки повороту.
  • Для малих амплітуд період фізичного маятника залежить тільки від моменту інерції тіла навколо точки повороту і відстані від стрижня до центру маси тіла. Він розраховується як:\mathrm{T=2π\sqrt{\frac{I}{mgh}}}.
  • Період ще не залежить від загальної маси жорсткого тіла. Однак він не є незалежним від масового розподілу жорсткого тіла. Зміна форми, розміру або розподілу маси змінить момент інерції і, отже, період.
  • Сума кінетичної і потенційної енергій в простому гармонічному осциляторі є постійною, т. Е\mathrm{KE+PE=constant}. Енергія коливається взад-вперед між кінетичним і потенційним, повністю переходячи від одного до іншого, коли система коливається.
  • У пружинній системі рівняння збереження записується так:\mathrm{\frac{1}{2}mv^2+\frac{1}{2}kx^2=constant=\frac{1}{2}kX^2}, де X - максимальне зміщення.
  • Максимальна швидкість залежить від трьох факторів: амплітуди, коефіцієнта жорсткості і маси:\mathrm{v_{max}=\sqrt{\frac{k}{m}}X}.
  • Для простих гармонічних осциляторів рівняння руху завжди є диференціальним рівнянням другого порядку, яке пов'язує прискорення та зміщення. Відповідними змінними є x, зміщення та k, постійна пружини.
  • Вирішення диференціального рівняння вище завжди дає рішення, які мають синусоїдальну природу. Наприклад,\mathrm{x(t), v(t), a(t), K(t),} і\mathrm{U(t)} всі мають синусоїдальні рішення для простого гармонійного руху.
  • Рівномірний круговий рух також є синусоїдальним, оскільки проекція цього руху поводиться як простий гармонічний генератор.

Ключові умови

  • період: Тривалість одного циклу в повторюваному заході.
  • Кутова частота: Кутове переміщення в одиницю часу.
  • частота: Частота числа разів n періодичного явища виникає за час t, в якому воно відбувається: f = n/t.
  • Відновлювальна сила: Змінна сила, яка породжує рівновагу у фізичній системі. Якщо система порушена від рівноваги, відновлювальна сила буде прагнути повернути систему до рівноваги. Відновлююча сила є функцією тільки положення маси або частки. Він завжди спрямований назад до положення рівноваги системи
  • амплітуда: Максимальне абсолютне значення деякої величини, яка змінюється.
  • простий гармонічний генератор: Пристрій, який реалізує закон Гука, такий як маса, яка прикріплена до пружини, а інший кінець пружини з'єднаний з жорсткою опорою, наприклад, стіною.
  • осцилятор: шаблон, який повертається до початкового стану, в тій же орієнтації та положенні, після кінцевої кількості поколінь.
  • доцентрове прискорення: Прискорення, яке змушує тіло слідувати вигнутому шляху: воно завжди перпендикулярно швидкості тіла і спрямоване до центру кривизни шляху.
  • рівномірний круговий рух: рух по круговому шляху з постійною швидкістю.
  • простий маятник: гіпотетичний маятник, що складається з ваги, підвішеної невагомою струною.
  • фізичний маятник: Маятник, де стрижень або струна не є безмасовим, і може мати розширений розмір; тобто довільної форми, жорстке тіло, що гойдається за допомогою шарніра. При цьому період маятника залежить від моменту його інерції навколо точки повороту.
  • розподіл маси: описує просторовий розподіл та визначає центр маси в об'єкті.
  • пружна потенційна енергія: Енергія, що зберігається в деформованому об'єкті, такому як пружина.
  • дисипативні сили: сили, які викликають втрату енергії в системі, що зазнає руху.
  • синусоїдальний: У формі хвилі, особливо тієї, амплітуда якої змінюється пропорційно синусу якоїсь змінної (наприклад, часу).

ЛІЦЕНЗІЇ ТА АВТОРСТВА

CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ