2.5: Статика

Коли множинні сили діють на тіло, (векторна) сума цих сил дає чисту силу, яка є силою, яку ми підставляємо у другому законі руху Ньютона, щоб отримати рівняння руху тіла. Якщо всі сили підсумувати до нуля, прискорення не буде, і тіло зберігає будь-яку швидкість, яку було раніше. Статика - це вивчення об'єктів, які в даний час не рухаються і не відчувають чистої сили, і, таким чином, залишаються нерухомими. Можна очікувати, що це дослідження легше, ніж динамічний випадок, коли тіла відчувають чисту силу, але це залежить лише від контексту. Уявіть, наприклад, банку, наповнену мармуром: вони не рухаються, але сили, що діють на кульки, звичайно не нульові, а також не рівномірно розподілені.

Навіть якщо немає чистої сили, немає гарантії, що об'єкт не буде проявляти руху: якщо сили розподілені нерівномірно по витягнутому об'єкту, він може почати обертатися. Обертання завжди відбуваються навколо нерухомої точки, відомої як стрижень. Тільки сила, яка має компонент, перпендикулярний лінії, що з'єднує його точку дії з шарніром (рукою), може змусити об'єкт обертатися. Відповідне кутове прискорення через силу залежить як від величини цієї перпендикулярної складової, так і від довжини руки, і відоме як момент сили або крутний момент\(\tau\). Величина крутного моменту, таким чином\(Fr sin\theta\),\(F\) задається, де величина сили, r довжина руки, і\(\theta\) кут між силою і рукою. Якщо записати плече як вектор r, що вказує від стрижня до точки, де діє сила, то виявимо, що величина крутного моменту дорівнює перехресному добутку\(r\) і\(F\):

\[\boldsymbol{\tau}=\boldsymbol{r} \times \boldsymbol{F}\]

Напрямок обертання можна знайти правилом правої руки від напрямку крутного моменту: якщо великий палець правої руки вказує уздовж напрямку\(\tau\), то напрямок, в якому ваші пальці криві, буде напрямок, в якому обертається об'єкт за рахунок дії відповідної сили \(F\).

Ротації ми детально вивчимо в главі 5. Наразі нас цікавить випадок, що немає руху, ні лінійного, ні обертального, а це означає, що сили і крутні моменти, що діють на наш об'єкт, повинні задовольняти умові стійкості: щоб витягнутий об'єкт був нерухомим, як сума сил, так і сума діючих на нього крутних моментів повинні дорівнювати нулю.

Приклад\(\PageIndex{1}\): Suspended Sign

Знак маси М висить підвішений на стрижні масою m і довжиною\(L\) симетрично і таким чином, щоб центри мас знака і стрижня красиво вирівнювалися (рис.\(\PageIndex{1a}\)). Один кінець стрижня закріплений безпосередньо на стіні, а інший підтримується дротом з незначною масою, яка прикріплена до тієї ж стіни на відстані h над якорем.

Малюнок\(\PageIndex{1}\): Підвішений знак (приклад розрахунку в статиці). (a) Налаштування проблеми. (б) Діаграма вільного тіла.

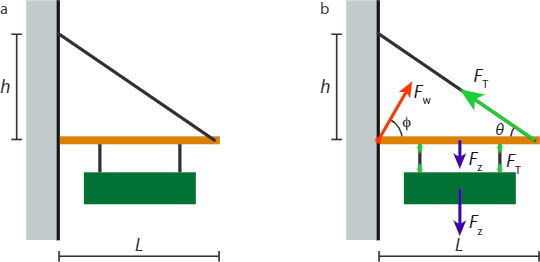
1. Якщо максимальний натяг, який може підтримувати провід, дорівнює Т, знайдіть мінімальне значення h.
2. Для того випадку, якщо натяг в дроті дорівнює максимальному натягу, знайдіть силу (величину і напрямок), що чиниться якорем на стрижень.

Рішення

(а) Спочатку малюємо діаграму вільного тіла, рис\(\PageIndex{1b}\). Силовий баланс на знаку говорить нам про те, що напруга в двох нижніх проводах підсумовується гравітаційній силі на знаку. Стрижень нерухомий, тому ми знаємо, що сума крутних моментів на ньому повинна зникнути. Щоб отримати крутний момент, нам спочатку потрібен шарнір; підбираємо точку, де стрижень закріплений на стіні. Потім у нас є три сили, що сприяють крутний момент за годинниковою стрілкою, і одна сприяє крутний момент проти годинникової стрілки Нам не сказали точно, де дроти прикріплені до стрижня, але нам кажуть, що конфігурація симетрична і що центр маси знака вирівнюється з тим, що стрижень. Нехай перший провід буде на відстані\(\alpha L\) від стіни, а другий - відстані\((1-\alpha)L\). Загальний (за годинниковою стрілкою) крутний момент, обумовлений гравітаційною силою на знак і стрижень, потім задається:

\[\tau_{\mathrm{Z}}=\frac{1}{2} m g L+\frac{1}{2} M g \alpha L+\frac{1}{2} M g(1-\alpha) L=\frac{1}{2}(m+M) g L. \nonumber\]

Крутний момент проти годинникової стрілки виходить від натягу в дроті, і задається

\[\frac{1}{2} m g L+\frac{1}{2} M g \alpha L+\frac{1}{2} M g(1-\alpha) L=\frac{1}{2}(m+M) g L. \nonumber\]

Прирівнювання двох крутних моментів дозволяє нам вирішити для має функцію\(F_T\), як просили, яка дає:

\[h^{2}=\left(\frac{1}{2} \frac{(m+M) g}{F_{\mathrm{T}}}\right)^{2}\left(h^{2}+L^{2}\right) \quad \rightarrow \quad h=\frac{(m+M) g L}{\sqrt{4 F_{\mathrm{T}}^{2}-(m+M)^{2} g^{2}}}\]

Знаходимо мінімальне значення h підставивши\(F_T=T_{max}\).

(б) Оскільки стрижень нерухомий, всі зусилля на ньому повинні скасовуватися. У горизонтальному напрямку маємо горизонтальну складову натягу, зліва,\(T_{max}\cos \theta\) яка повинна дорівнювати горизонтальній складовій сили, що чиниться стіною,\(F_w cos \phi\). У вертикальному напрямку маємо гравітаційну силу і дві сили від проводів, на яких знак висить в напрямку вниз, і вертикальну складову натягу в дроті у напрямку вгору, сума яких повинна дорівнювати вертикальної складової сили, що чиниться стіною (яка може вказувати або вгору, або вниз). Таким чином, ми маємо

\[\begin{align*} F_{\mathrm{w}} \cos \phi &=T_{\max } \cos \theta \\[4pt] F_{\mathrm{w}} \sin \phi &=(m+M) g+T_{\max } \sin \theta \end{align*}\]

де\(\tan \theta={h \over L}\) і\(h\) дається у відповіді на (а). Ми знаходимо, що

\[\begin{align*} F_{\mathrm{w}}^{2} &=T_{\mathrm{max}}^{2}+2(m+M) g T_{\max } \sin \theta+(m+M)^{2} g^{2} \\[4pt] \tan \phi &=\frac{T_{\max } \cos \theta}{(m+M) g+T_{\max } \sin \theta} \end{align*}\]

Зверніть увагу, що наведені вище вирази дають повну відповідь (величину і напрямок). Ми могли б усунути\(h\) і\(\theta\), але це буде просто алгебра, що призводить до більш складних виразів, і не дуже корисно в себе.Якщо нас попросили обчислити висоту або силу для будь-яких конкретних значень M, m і L, ми могли б отримати відповіді легко підставивши числа в наведені тут вирази.