3.4: Багатовимірне обчислення

Що таке розділ про багатовимірне обчислення робити в книзі фізики... зокрема книга фізики, яка передбачає, що ви вже знаєте багатовимірне обчислення? Відповідь полягає в тому, що ви пройшли через свій багатовимірний курс обчислення, вивчаючи одну тему за іншою, і є деякі тонкі теми, які ви висвітлювали на початку курсу, які дійсно не могли бути належним чином зрозумілі, поки ви не охопили інші теми, які прийшли пізніше в курсі. (Це не вина вашого вчителя в багатоваріантному обчисленні, тому що пізніші теми взагалі не могли бути зрозумілі без впливу на більш ранні теми.) Цей розділ повертається назад і досліджує п'ять тонких точок з багатовимірного обчислення, щоб переконатися, що вони не сполучають вас, коли вони застосовуються до термодинаміки.

3.4.1 Що таке часткова похідна?

З огляду на функцію f (x, y, z), яке значення f /y? Багато хто відповість, що

$$\frac{\partial f}{\partial y} \text { is the change of } f \text { with } y \text { while everything else is held constant. }$$

Ця відповідь НЕПРАВИЛЬНА! Якщо f змінюється, то f ² зміни, а sin (f) змінюється і так далі, тому не може бути, що «все інше» тримається постійним. Правильна відповідь полягає в тому, що

$$\frac{\partial f}{\partial y} \text { is the change of } f \text { with } y \text { while all other variables are held constant. }$$

Таким чином, важливо чітко розуміти, які величини є змінними, а які є функціями. Зазвичай це не важко в контексті математики: функціями є f, g та h, тоді як змінні - x, y та z. Але в контексті фізики ми використовуємо символи, такі як E, V, p, T і N які припускають величини, які вони представляють, і легко змішати функції та змінні.

Ілюстрація з геометрії робить цей момент дуже добре. Розглянемо набір всіх правильних кругових циліндрів. Кожен циліндр може бути однозначно заданий змінними r, радіусом і h, висотою. Якщо ви знаєте r і h для циліндра, ви можете легко обчислити будь-яку цікаву кількість - наприклад, площа верхньої частини, T (r, h), площа сторони S (r, h) та об'єм V (r, h) - як показано в лівій частині таблиці нижче. Але це не єдиний спосіб однозначно вказати кожен циліндр. Наприклад, якщо ви знаєте висоту і бічну площу циліндра, ви можете легко обчислити радіус і, отже, знайти нашу попередню специфікацію. Дійсно, специфікація через змінні S і h так само хороша, як і через змінні r і h, як показано в правій частині таблиці нижче. [Є багато інших можливих специфікацій (наприклад, r і S, або T і V), але цих двох наборів буде достатньо, щоб зробити нашу точку зору.]

Опис циліндра

$\begin{array}{cl}{\textbf{ variables: }} & {\textbf{ variables: }} \\ {\text { radius } r} & {\text { side area } S} \\ {\text { height } h} & {\text { height } h} \\ {\textbf{ functions: }} & {\textbf{ functions: }} \\ {\text { top area } T(r, h)=\pi r^{2}} & {\text { radius } r(S, h)=S / 2 \pi h} \\ {\text { side area } S(r, h)=2 \pi r h} & {\text { top area } T(S, h)=S^{2} / 4 \pi h^{2}} \\ {\text { volume } V(r, h)=\pi r^{2} h} & {\text { volume } V(S, h)=S^{2} / 4 \pi h}\end{array}$

Все це досить просто і буденно. Але тепер ми задаємо ще одне питання, що стосується геометрії циліндрів, а саме «Як змінюється обсяг з висотою?» В останньому рядку таблиці представлені дві формули для обсягу, тому прийняття відповідної похідної дає нам або

$$\frac{\partial V}{\partial h}=\pi r^{2}=T \quad \text { or } \quad \frac{\partial V}{\partial h}=-S^{2} / 4 \pi h^{2}=-T.$$

Що? V /h дорівнює T або − T? Це не може бути рівним обом! Проблема з рівнянням (3.11) полягає в тому, що ми недбало ставилися до вказівки змінних. Два вирази для обсягу,

$$V(r, h)=\pi r^{2} h \quad \text { and } \quad V(S, h)=S^{2} / 4 \pi h,$$

насправді дві абсолютно різні функції, з абсолютно різними змінними, тому слід очікувати абсолютно різних похідних. Якщо збільшити висоту h зберігаючи радіус r фіксованим, то цифра зліва внизу дає зрозуміти, що обсяг збільшується. Але якщо ми збільшимо висоту і збережемо бічну область S фіксованою, радіус доведеться зменшити, як показано праворуч нижче. Зміна праворуч додає гучності у верхній частині циліндра, але віднімає від обсягу з усіх боків. Було б найбільш примітно, якби дві зміни обсягу були рівними, і, як показали наші похідні, вони не є.

Математик сказав би, що ми потрапили в біду в рівнянні (3.11), тому що ми дали дві різні функції однакове ім'я. Фізик відповів би, що вони обидва представляють обсяг, тому вони заслуговують на одне і те ж ім'я. Замість того, щоб потрапити в аргумент, найкраще виписати змінні всіх функцій явно, таким чином переписуючи (3.11) як

$$\frac{\partial V(r, h)}{\partial h}=\pi r^{2}=T(r, h) \quad \text { or } \quad \frac{\partial V(S, h)}{\partial h}=-S^{2} / 4 \pi h^{2}=-T(S, h).$$

(Фізики часто нехтують виписуванням повного списку змінних, що економить деякий час і трохи чорнила, але яке запрошує помилку. Р.Х. Прайс і Дж.Д. Романо (Am. Дж. фіз. 66 (1998) 114) викривають ситуацію, в якій фізик опублікував глибоку помилку, яку він зробив, нехтуючи виписувати явний список змінних.)

Виписувати весь список аргументів для кожної функції стає втомливим, тому було розроблено стенографічне позначення. Права дужка пишеться після часткової похідної, а функціональні аргументи, які не диференціюються, перераховуються як індекси цієї дужки. Таким чином, наведені вище похідні пишуться як

$$\frac{\partial V(r, h)}{\partial h}=\frac{\partial V}{\partial h} )_{r} \quad \text { and } \quad \frac{\partial V(S, h)}{\partial h}=\frac{\partial V}{\partial h} )_{S}.$$

Вираз зліва читається «часткова похідна V по відношенню до h, тоді як r тримається постійною».

3.4.2 Перетворення Лежандра

Повернемося до опису циліндрів через змінні r і h. ясно, що однією з функцій, що цікавлять, є обсяг.

$$V (r, h).$$

Погляд на таблицю на сторінці 58 (або думка моменту про геометрію) показує, що сумарний диференціал V як функції r і h дорівнює

$$d V=S(r, h) d r+T(r, h) d h,$$

звідки

$$S(r, h)=\frac{\partial V}{\partial r} )_{h} \quad \text { and } \quad T(r, h)=\frac{\partial V}{\partial h} )_{r}.$$

Таким чином знання функції V (r, h) дає нам бонус.. якщо ми знаємо V (r, h), то ми можемо взяти прості похідні, щоб знайти інші величини, що цікавлять, що стосуються циліндрів, а саме S (r, h) і T (r, h). Через центральне значення V (r, h) його називають «головною функцією», а загальний диференціал (3.16) називається «майстер-рівнянням».

Чи є спосіб знайти аналогічно зручний «майстер-опис» з точки зору змінних S і h? Дійсно є, і воно дається «Лежандровим перетворенням». При перетворенні Лежандра зі змінних r і h в змінні S і h змінюємо фокус нашої уваги з головної функції V (r, h) на функцію

$$\Phi(S, h)=V(r(S, h), h)-S r(S, h).$$

(Вищевказане рівняння виписано в повному обсязі з усіма показаними аргументами. Це частіше розглядається як

$$\Phi=V-S r,$$

хоча ця форма підвищує можливість того, що змінні та функції стануть змішаними.) Загальний диференціал Φ дорівнює

$$d \Phi =d V-S d r-r d S$$

$$=S d r+T d h-S d r-r d S$$

$$=-r d S+T d h$$

Ми знайшли нову головну функцію! Це

$$\Phi(S, h),$$

і нове майстер рівняння

$$d \Phi=-r(S, h) d S+T(S, h) d h,$$

породжуючи негайно

$$r(S, h)=-\frac{\partial \Phi}{\partial S} )_{h} \quad \text { and } \quad T(S, h)=\frac{\partial \Phi}{\partial h} )_{S}.$$

Цей опис має всі характеристики головного опису: як тільки головна функція відома, всі інші цікаві функції можна знайти, взявши прості похідні.

3.4.3 Відносини Максвелла

Припустимо

$$df = A(x, y) dx + B(x, y) dy. (3.26)$$

Тоді

$A(x, y)=\frac{\partial f}{\partial x} )_{y} \quad \text { and } \quad B(x, y)=\frac{\partial f}{\partial y} )_{x}.$

Але тому, що

$\frac{\partial^{2} f(x, y)}{\partial x \partial y}=\frac{\partial^{2} f(x, y)}{\partial y \partial x}$

з цього випливає, що

$$\frac{\partial A}{\partial y} )_{x}=\frac{\partial B}{\partial x} )_{y}.$$

Це називається «відношення Максвелла».

Застосовується до рівняння (3.16), це говорить нам з першого погляду, що

$$\frac{\partial S}{\partial h} )_{r}=\frac{\partial T}{\partial r} )_{h}.$$

Ми знаємо, що ці дві похідні рівні без необхідності знаходити жодну з них! Застосовується до рівняння (3.24), він говорить нам з однаковою легкістю, що

$$\frac{\partial r}{\partial h} )_{S}=-\frac{\partial T}{\partial S} )_{h}.$$

3.4.4 Теорема про неявні функції

Припустимо, f (x, y) є функцією змінних x і y. Що таке

$$\frac{\partial y}{\partial x} )_{f}$$

нахил контуру контуру постійної f?

Почніть з

$$d f=\frac{\partial f}{\partial x} )_{y} d x+\frac{\partial f}{\partial y} )_{x} d y.$$

який тримає для будь-якої диференціальної зміни dx і dy. Але нас не цікавить будь-яка диференціальна зміна: щоб оцінити нахил (3.30), нам потрібна зміна, в якій df = 0 так

$0=\frac{\partial f}{\partial x} )_{y} d x+\frac{\partial f}{\partial y} )_{x} d y \quad \text { with } d x, d y \text { on contour of } f.$

Таким чином

$\frac{d y}{d x}=-\frac{\frac{\partial f}{\partial x} )_{y}}{\frac{\partial f}{\partial y} )_{x}} \quad \text { with } d x, d y \text { on contour of } f$

і, записуючи обмеження «з dx, dy по контуру f» в символи рівняння,

$$\frac{\partial y}{\partial x} )_{f}=-\frac{\frac{\partial f}{\partial x} )_{y}}{\frac{\partial f}{\partial y} )_{x}}.$$

Зверніть увагу, що ви отримаєте неправильну відповідь, якщо «скасуєте невелику кількість f від чисельника та знаменника співвідношення». Це тому, що «мала кількість f з постійною y» відрізняється від «малої кількості f з постійною x». Мені потрібно написати кілька слів і цифру про те, чому.

3.4.5 Правило мультиварки ланцюга

Припустимо, f (x, y) і g (x, y) є двома функціями змінних x і y. Тоді знову у нас є

$$d f=\frac{\partial f}{\partial x} )_{y} d x+\frac{\partial f}{\partial y} )_{x} d y$$

для будь-якої диференціальної зміни dx і dy.

Що робити, якщо нас цікавить не будь-яка зміна, а зміна по контуру постійної g? Зокрема, що робити, якщо нам потрібно знайти зміну f з x під час переміщення по контуру постійної g? Потім просто візьміть точний диференціал вище і застосуйте його до зміни dx, dy по контуру з постійною g. Ділимо на диференціальну величину dx:

$\frac{d f}{d x}=\frac{\partial f}{\partial x} )_{y} \frac{d x}{d x}+\frac{\partial f}{\partial y} )_{x} \frac{d y}{d x}=\frac{\partial f}{\partial x} )_{y}+\frac{\partial f}{\partial y} )_{x} \frac{d y}{d x} \quad \text { with } d x, d y \text { on contour of } g$

Тепер запишіть обмеження «з dx, dy на контурі g» в символи рівняння, щоб знайти

$$\frac{\partial f}{\partial x} )_{g}=\frac{\partial f}{\partial x} )_{y}+\frac{\partial f}{\partial y} )_{x} \frac{\partial y}{\partial x} )_{g},$$

правило мультиварки ланцюга.

Проблеми

3.9 Часткові похідні у просторі

Точку на площині можна вказати або змінними (x, y) або змінними (x ', y'), де

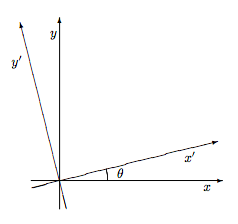
$$\begin{aligned} x^{\prime} &=+\cos (\theta) x+\sin (\theta) y \\ y^{\prime} &=-\sin (\theta) x+\cos (\theta) y \end{aligned}.$$

Якщо f (x, y) є деякою функцією розташування на площині, то пишіть вирази для

$$\frac{\partial f}{\partial x^{\prime}} )_{y^{\prime}}, \quad \frac{\partial f}{\partial y^{\prime}} )_{x^{\prime}}, \quad \text { and } \quad \frac{\partial f}{\partial x} )_{y^{\prime}}$$

в перерахунку на

$$\frac{\partial f}{\partial x} )_{y} \quad \text { and } \quad \frac{\partial f}{\partial y} )_{x}.$$

Інтерпретувати f /x) _y' геометрично як спрямовану похідну. (Тобто f /x) _y' - нахил f, вздовж якої кривої в площині?) Враховуючи це тлумачення, чи має вона очікувані межі як θ → 0 і як θ → π/2?

3.10 Відносини Максвелла для тризмінної системи

Припустимо, Φ (x, y, z) задовольняє

$$d \Phi=A(x, y, z) d x+B(x, y, z) d y+C(x, y, z) d z.$$

Створіть три відносини Максвелла, що стосуються різних перших похідних A (x, y, z), B (x, y, z) та C (x, y, z), і четверте відношення Максвелла, що стосуються різних других похідних цих функцій.

3.11 Модель циліндра з трьома змінними

У «моделі тризмінних циліндрів» циліндри описуються висотою h, радіусом r і щільністю ρ. Головною функцією є маса M (h, r, ρ), а основне рівняння -

$$d M(h, r, \rho)=\rho S(h, r) d r+\rho T(r) d h+V(h, r) d \rho ,$$

де S (h, r) - бічна область, T (r) - верхня область, а V (h, r) - об'єм. Виконати перетворення Лежандра до опису через змінні h, S та ρ за допомогою нової головної функції

$$\Phi(h, S, \rho)=M-\rho S r.$$

а Запишіть нове основне рівняння.

б Запишіть три відносини Максвелла першого порядку і підтвердіть їх правильність за допомогою явних формул, таких як M (h, S, ρ) = ρs ²/(4π h).

c Інтерпретувати Φ (h, S, ρ) фізично.

3.12 Правило мультиварки ланцюга

Придумайте проблему, що проходить через аргумент правила ланцюга розділу 3.8.1 з моделлю циліндра.

3.13 Контури постійної бічної площі

Знайти контури постійної бічної площі підготовки/використовуючи техніку розділу 3.8.3.