3.2: Ентропія

\( \begin{aligned} d E &=T d S-p d V+\mu d N \\ &=d Q+d W_{\mathrm{conf}}+d W_{\mathrm{diss}} \\ & \geq d Q+d W_{\mathrm{conf}} \end{aligned}.\)

проте

\( d W_{\mathrm{conf}}=-p d V+\mu d N\)

тому

\( T d S>d Q\)

де рівність має місце для квазістатичних змін.

Оперативне визначення ентропії полягає в тому, що для квазістатичної зміни

\[d S=\frac{d Q}{T}. \label{3.3}\]

Якщо ми зайдемо в лабораторію з таким визначенням ентропії, експериментатор скаже: «Звичайно, я можу знайти цю величину. У мене є термометри; і у мене є резистори, амперметри та вольтметри, а також процедура їх використання для розрахунку теплового потоку».

За будь-які зміни (можливо квазістатичні, можливо, ні)

\[d S \geq \frac{d Q}{T}.\]

(Зміна ентропії може бути обумовлена теплом, може бути обумовлена дисипативною роботою, може бути пов'язана з поєднанням цих двох.)

Конфігураційна ентропія проти теплової ентропії

Оперативне термодинамічне визначення ентропії, Equation\ ref {3.3}, фактично було виявлено ще до більш фундаментального, концептуального, статистичного визначення (2.7). Через це подвійне визначення деякі люди отримують помилкове уявлення про те, що існує два види ентропії: статистичний вид («конфігураційна ентропія») та операційний вид («теплова ентропія»). Це брехня. Це два різних способи погляду на одне і те ж.

3.2 (I) Ідеальний газ зі змінними S і V.

a. використовувати рівняння (2.32), щоб показати, що для зразка одноатомного ідеального газу з фіксованою кількістю частинок енергетична функція дорівнює

\[E(S, V)=E_{0}\left(\frac{V_{0}}{V}\right)^{2 / 3} e^{S / S_{0}},\]

де E ₀, V ₀ і S ₀ - константи з розмірами енергії, об'єму та ентропії.

б. використовуйте формули

\[ T(S, V)=\frac{\partial E(S, V)}{\partial S} \quad \text { and } \quad p(S, V)=-\frac{\partial E(S, V)}{\partial V}\]

знайти функції температури і тиску для цього зразка.

3.3 (I) Залежність теплоти і роботи від шляху

Припустимо, що зразок ідеального газу, згаданий у попередній задачі, зазнає зміни від початкового стану з об'ємом V ₀ та ентропією S ₀ до кінцевого стану з об'ємом 8 V ₀ та ентропією (1+ 5 ln 2) S ₀. Існує нескінченна кількість квазістатичних шляхів, які виконують цю зміну. Наприклад:

A Спочатку збільште ентропію від S = S ₀ до S = (1 + 5 ln 2) S ₀, зберігаючи обсяг фіксованим при V = V ₀, потім розширити від V = V ₀ до V = 8 V ₀, зберігаючи ентропію фіксованою при S = (1 + 5 ln 2) S ₀.

B Збільшення гучності і ентропії одночасно по шляху

\[ S(V)=S_{0}\left[\frac{5}{3} \ln \left(\frac{V}{V_{0}}\right)+1\right].\]

C Спочатку розгорніть від V = V ₀ до V = 8 V ₀, зберігаючи ентропію фіксованою при S = S ₀, потім збільште ентропію від S = S ₀ до S = (1 + 5 ln 2) S ₀, зберігаючи обсяг фіксованим при V = 8 V ₀.

Кожен шлях має однакову зміну об'єму, ентропії та енергії, але кожен матиме різну теплоту та роботу. (Пам'ятайте, що кожен шлях квазістатичний.)

а. розрахуйте тепло, поглинене зразком, і роботу, виконану над зразком для кожного з цих трьох шляхів.

b. знайти різницю Q + W для кожного з цих трьох шляхів.

с. четвертий шлях від початкового до кінцевого стану передбачає неквазістатичну зміну і поглинання тепла Q = 3 E ₀. Які роботи виконуються за зразком під час цієї зміни?

(При складанні цієї проблеми я вибираю дещо своєрідні початкові та кінцеві стани та сполучні шляхи, щоб наведені вище величини можна було обчислити аналітично. Незважаючи на ці особливості, принцип, проілюстрований проблемою, повинен бути зрозумілим: тепло і робота залежать від шляху, але їх різниця в зміні енергії не має.)

3.4 (I*) Робота в розрізі p і V

Ми досі розглядали роботу та тепло в системі рідини, заданої змінними S, V і N, і часто припускали, що N є постійною. Інший спосіб вказівки такої системи - через змінні p (тиск) і V. Ця задача розглядає квазістатичні процеси, описані як шляхи в площині (p, V).

а. показати, що робота, виконана над системою при зміні квазістатично від початкового стану (V _i, p _i) до кінцевого стану (V _f, p _f) по шляху, показаному на малюнку нижче, є негативом площі під кривою. Яка робота виконується, якщо шлях пройдений в зворотному напрямку?

б Яка робота проводиться в системі за допомогою тієї ж зміни по шляху нижче?

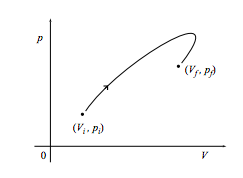
c Нарешті, яка робота виконується над системою, якщо вона повернеться до початкової точки, як у циклі, показаному нижче? Що робити, якщо цикл замість цього виконується проти годинникової стрілки?

3.5 (I) Робота рідини

При квазістатичному, адіабатичному процесі зразок газу розширюється від V _i = 1 м ³ до V _f = 8 м ³, при цьому тиск падає від p _i = 32 Па до p _f = 1 Па. Помічено, що під час цього процесу тиск і обсяг пов'язані

\[p V^{\gamma}=\text { constant },\]

де постійна γ є\( \frac{5}{3}\). Звичайно, це не єдиний процес, що веде від цього конкретного початкового стану до цього конкретного кінцевого стану. Знайдіть загальну роботу, виконану над системою і тепло, поглинене системою в кожному з наступних квазістатичних процесів, всі з яких з'єднують однакові два термодинамічних стану.

а. адіабатичний процес, описаний вище.

б. при постійному тиску газ розширюється від V _i до V _f. (Тепло необхідно додати в систему під час цього розширення, щоб підтримувати тиск постійним.) Потім при постійному обсязі тиск знижується від p _i до p _f. (Тепло повинно бути витягнуто з системи на цьому етапі процесу.)

c Обсяг збільшується і тепло подається з правильною швидкістю, щоб тиск зменшувався лінійно з об'ємом.

d. як і в частині (б.), але з двома кроками, виконаними в протилежному порядку.