6.7: Дифракція Фраунгофера переглянута

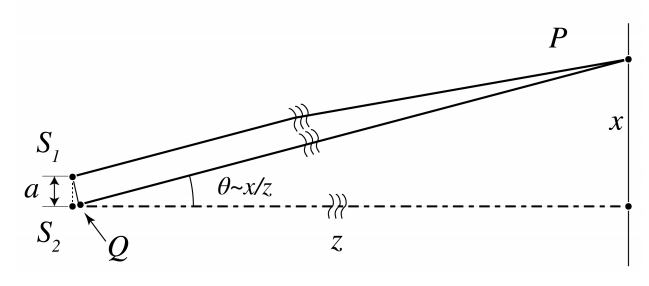
Дифракційні закономірності Фраунгофера можна якісно пояснити, розглядаючи напрямки, в яких відбувається деструктивне і конструктивне втручання. Розглянемо два взаємно когерентних$S_{1}, S_{2}$ точкових джерела на$x$ -осі, як показано на малюнку$\PageIndex{1}$. Ми припускаємо, що ці точкові джерела знаходяться в фазі. На екрані на великій відстані спостерігається$z$ інтерференційна картина. Якщо відстань$z$ екрану дуже велика, сферичні хвильові фронти, випромінювані точковими джерелами, майже плоскі біля екрану. У точці$P$ на екрані на відстані$x$ вище$z$ -осі оптичні відмінності шляху хвиль, випромінюваних двома джерелами, приблизно задаються$S_{2} Q=a \theta$, де$\theta=x / z$ передбачається невеликим. Звідси конструктивні інтерференції виникають для кутів,$\theta$ таких, що$S_{2} Q=m \lambda$ для деякого цілого числа$m$, тобто коли

$$\theta=m \frac{\lambda}{a}, \quad \text { constructive interference. } \nonumber$$

Руйнівні перешкоди виникають, коли різниця довжини шляху задовольняє$S_{2} Q=\lambda / 2+m \lambda$ деяке ціле число$m$, отже, для кутів

$$\theta=(m+1 / 2) \frac{\lambda}{a} \quad \text { destructive interference. } \nonumber$$

Якщо точкові джерела мають однакову міцність, їх поля відмінно скасовуються для цих кутів.

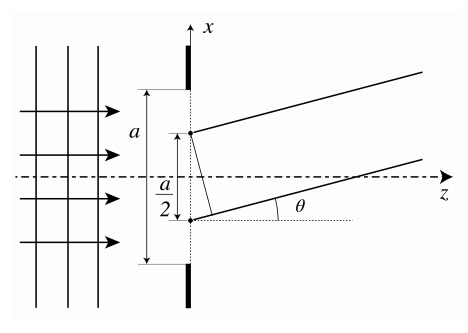
Тепер розглянемо щілину, як показано на малюнку$\PageIndex{2}$, яка освітлена перпендикулярною падаючою площиною хвилею. За принципом Гюйгенса-Френеля поле на екрані, далекому від щілини, - це сума полів точкових джерел в діафрагмі. Оскільки щілина висвітлюється плоскою хвилею при перпендикулярному падінні, всі точкові джерела знаходяться в фазі і мають однакову міцність. Розділіть щілину на дві рівні половини, як показано на малюнку$\PageIndex{2}$. Точкові джерела в щілині можуть бути розташовані на пари, з яких один точковий джерело знаходиться у верхній половині щілини, а інший знаходиться в еквівалентному положенні (на відстані$a / 2$ від іншого точкового джерела) в нижній половині щілини. $\theta$Дозволяти кут, для якого два точкові джерела пари скасовують один одного тобто

$$\theta=(m+1 / 2) \frac{\lambda}{a / 2}=(1+2 m) \frac{\lambda}{a}, \nonumber$$ так як відстань між точковими джерелами є$a / 2$. Переводячи пару точкових джерел через щілини, випливає, що обидві половинки щілини відмінно скасовують один одного для цих кутів.

Малюнок$\PageIndex{1}$: Інтерференція взаємно когерентних точкових джерел. Для$z$ дуже великих точок,$P$ де виникають конструктивні і руйнівні перешкоди, такі, що для деяких цілих$m: S_{2} Q=m \lambda$ і$S_{2} Q=(1 / 2+m) \lambda$, відповідно

Малюнок$\PageIndex{2}$: Діливши щілину на дві щілини розміром$a / 2$ кожна і враховуючи пари точкових джерел, з яких одна знаходиться в одній половині щілини, а інша знаходиться у відповідному положенні в іншій половині, кути, де між цими точковими джерелами виникає руйнівна перешкода призводять до мінімумів у дифракційній схемі. Зверніть увагу, що точкові джерела мають відповідні положення в двох частинях щілини, якщо їх відстань дорівнює$a / 2$.

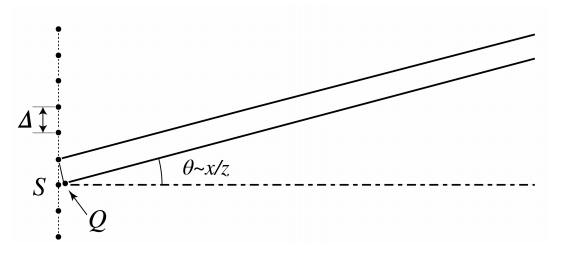
Далі розглянемо дифракційну решітку з періодом$\Delta$. З малюнка випливає,$\PageIndex{3}$ що між сусідніми періодами, а значить, і для всіх періодів будуть конструктивні перешкоди, для кутів, для яких відстань$S Q$ на рис$\PageIndex{3}$ кратна довжині хвилі, тобто для

$$\theta=m \frac{\lambda}{\Delta} \text {, } \nonumber$$ яких відповідає напрямку дифракційні порядки. Для інших кутів фази полів різних періодів сильно відрізняються, і тому поля майже скасовуються під цими кутами.

Це пояснює, що для дифракційної решітки, що складається з багатьох періодів, інтенсивність далекого поля висока тільки в певних напрямках, в залежності від довжини хвилі і періоду дії решітки.

Малюнок$\PageIndex{3}$: Якщо кут$\theta$ такий, що$S Q$ кратний довжині хвилі, конструктивно заважають два суміжних періоду, а значить і всі періоди решітки. Ці кути відповідають порядку дифракції.