6.6: Наближення Френеля та Фраунгофера

Наближення Френеля і Фраунгофера - це два наближення інтеграла Релей-Зоммерфельда (6.13). Наближення базуються на припущенні, що поле поширювалося на досить велику відстань$z$. У наближенні Фраунгофера,$z$ має бути дуже великим, тобто набагато більшим, ніж для наближення Френеля, щоб провести. Якщо говорити по-іншому: у порядку найбільш точної та найменш точної (тобто дійсної лише для великих відстаней поширення), дифракційні інтеграли будуть оцінюватися як:

[Найбільш точний]$\quad$ Рейлі-Зоммерфельд$\rightarrow$ Френель$\rightarrow$ Фраунгофер$\quad$ [Найменш точний].

Малюнок$\PageIndex{1}$: Демонстрація ролей різних просторових частот. Видаляючи високі просторові частоти, залишаються лише широкі риси зображення: ми втрачаємо роздільну здатність. Якщо низькі просторові частоти видаляються, залишаються лише різкі риси (тобто контури) на зображенні.

Рисунок$\PageIndex{2}$: Демонстрація ролі фази просторового перетворення Фур'є. Якщо інформація про амплітуду видаляється, але інформація про фазу зберігається, деякі особливості вихідного зображення все ще впізнаються. Однак, якщо інформація про фазу видаляється, але інформація про амплітуду зберігається, вихідне зображення повністю втрачається.

6.5.1 Наближення Френеля

Для обох наближень ми припускаємо, що$z$ в Eq. (6.3.1) настільки великий, що в знаменнику ми можемо наблизити$r \approx z$ $$\begin{aligned} U(x, y, z) &=\frac{1}{i \lambda} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) \frac{z}{r} \frac{e^{i k r}}{r} \mathrm{~d} x^{\prime} \mathrm{d} y^{\prime} \\ & \approx \frac{1}{i \lambda z} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) e^{i k r} \mathrm{~d} x^{\prime} \mathrm{d} y^{\prime} . \end{aligned} \nonumber$$

Причина, чому ми не можемо застосувати те саме наближення для показника, полягає$r$ в тому, що там$r$ множиться на$k=2 \pi / \lambda$, що дуже велике, тому будь-яка помилка, введена наближенням,$r$ буде значно збільшена на $k$а потім може привести до зовсім іншого значення$\exp (i k r)=\cos (k r)+i \sin (k r)$. Щоб$r$ наблизитися до показника,$\exp (i k r)$ ми повинні бути обережнішими і замість цього застосувати розширення Тейлора. Нагадаємо, що $$\begin{aligned} r &=\sqrt{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}+z^{2}} \\ &=z \sqrt{\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{z^{2}}+1} . \end{aligned} \nonumber$$

Ми знаємо, що за невелику кількість$s$ ми можемо розширити $$\sqrt{s+1}=1+\frac{s}{2}-\frac{s^{2}}{8}+\ldots . \nonumber$$

Оскільки ми припускали, що$z$ великий,$\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{z^{2}}$ є маленьким, тому ми можемо розширити $$\begin{aligned} r &=z \sqrt{\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{z^{2}}+1} \\ & \approx z\left(1+\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{2 z^{2}}\right) \\ &=z+\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{2 z}, \quad \text { Fresnel approximation. } \end{aligned} \nonumber$$

З цим наближенням ми дійдемо до дифракційного інтеграла Френеля, який можна записати в наступних еквівалентних формах: $$\begin{aligned} U(x, y, z) & \approx \frac{e^{i k z}}{i \lambda z} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) e^{\frac{i k}{2 z}\left[\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}\right]} \mathrm{d} x^{\prime} \mathrm{d} y^{\prime} \\ &=\frac{e^{i k z} e^{\frac{i k\left(x^{2}+y^{2}\right)}{2 z}}}{i \lambda z} \iint U_{0}\left(x^{\prime}, y^{\prime}\right) e^{\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}} e^{-i k\left(\frac{x}{z} x^{\prime}+\frac{y}{z} y^{\prime}\right)} \mathrm{d} x^{\prime} \mathrm{d} y^{\prime} \\ &=\frac{e^{i k z} e^{\frac{i k\left(x^{2}+y^{2}\right)}{2 z}}}{i \lambda z} \mathcal{F}\left\{U_{0}\left(x^{\prime}, y^{\prime}\right) e^{\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}}\right\}\left(\frac{x}{\lambda z}, \frac{y}{\lambda z}\right) . \end{aligned} \nonumber$$

Особливо цікавий останній вислів, адже воно показує, що

Інтеграл Френеля - це перетворення Фур'є поля,$U_{0}\left(x^{\prime}, y^{\prime}\right)$ помножене на пропагатор Френеля$\exp \left(\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}\right)$.

Зверніть увагу, що цей пропагатор залежить від відстані розмноження$z$.

Зауваження. За допомогою перетворення$(\(\PageIndex{6}$)\) Фур'є отримують амплітуди плоских хвиль інтеграла Френеля. Виходить, що ці амплітуди рівні$\mathcal{F}\left(U_{0}\right)$ помножені на фазовий коефіцієнт. Цей фазовий фактор є параксіальним наближенням точного фазового фактора$\exp \left(i z k_{z}\right)$, заданого, тобто він містить як показник параболічного наближення$k_{z}$. Тому наближення Френеля ще називають параксиальним наближенням. Фактично, можна показати, що дифракційний інтеграл Френеля є розв'язком параксіального хвильового рівняння і навпаки, що кожен розв'язок параксиального хвильового рівняння може бути записаний як дифракційний інтеграл Френеля.

6.5.2 Наближення Фраунгофера

Для наближення Фраунгофера зробимо ще одне наближення до$r$ в$\exp (i k r)$ $$\begin{aligned} r & \approx z+\frac{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}{2 z} \text { Fresnel approximation } \\ & \approx z+\frac{x^{2}+y^{2}-2 x x^{\prime}-2 y y^{\prime}}{2 z} \text { Fraunhofer approximation. } \end{aligned} \nonumber$$

Отже, ми опустили квадратичні члени$x^{\prime 2}+y^{\prime 2}$, і порівняно з дифракційним інтегралом Френеля, ми просто опускаємо коефіцієнт,$\exp \left(\frac{i k\left(x^{\prime 2}+y^{\prime 2}\right)}{2 z}\right)$ щоб отримати дифракційний інтеграл Фраунгофера: $$U(x, y, z) \approx \frac{e^{i k z} e^{\frac{i k\left(x^{2}+y^{2}\right)}{2 z}}}{i \lambda z} \mathcal{F}\left(U_{0}\right)\left(\frac{x}{\lambda z}, \frac{y}{\lambda z}\right) \nonumber$$

Це призводить до наступного важливого спостереження:

Дальнє поле Фраунгофера$U_{0}\left(x^{\prime}, y^{\prime}\right)$ - це просто його перетворення Фур'є з додатковим квадратичним фазовим коефіцієнтом.

Зверніть увагу, що координати, за якими ми повинні оцінювати$\mathcal{F}\left(U_{0}\right)$ масштаб$1 / z$, і$U(x, y, z)$ загальне поле пропорційне$1 / z$. Це означає, що коли ви вибираєте$z$ більше (тобто ви поширюєте поле далі), поле просто розтікається, не змінюючи своєї форми, а його амплітуда знижується. Зазначено по-різному,$1 / z$ крім фактора перед інтегралом, поле Фраунгофера залежить тільки від кутів$x / z$ amd$y / z$. Тому поле розходиться у міру$z$ збільшення відстані поширення.

Зрештою, для досить великих відстаней поширення, тобто в межі Фраунгофера, світло завжди поширюється, не змінюючи форми розподілу світла.

Зауваження.

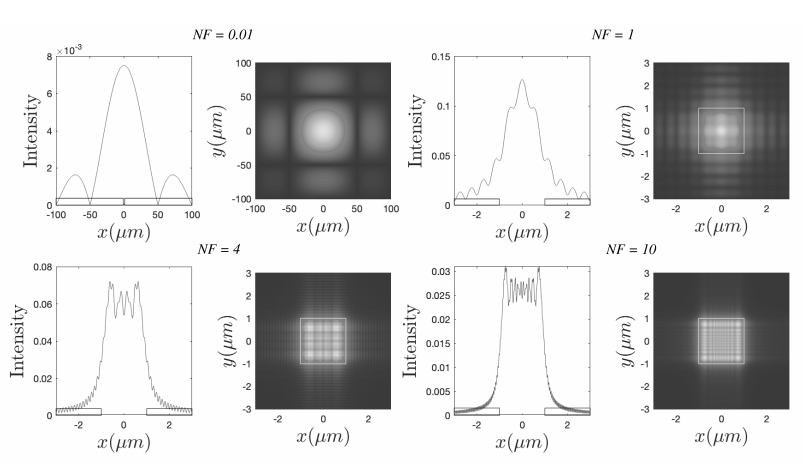
1. Інтеграл Френеля, як і інтеграл Фраунгофера, також перетворення Фур'є, оцінюється в просторових частотах, які залежать від точки спостереження: $$\xi=\frac{x}{\lambda z}, \quad \eta=\frac{y}{\lambda z} . \nonumber$$ Однак, на відміну від інтеграла Фраунгофера, інтеграл Френеля додатково по-іншому залежить від відстані поширення $z$, А саме через експонент пропагатора в цілісному. Це причина того, що інтеграл Френеля не просто залежить від$z$ через співвідношення$x / z$ і,$y / z$ але більш складним чином. Тому інтеграл Френеля дає досить різноманітні візерунки в залежності від величини відстані поширення$z$, як показано на малюнку$\PageIndex{4}$.
2. $f_{a, b}(x, y)=f(x-a, y-b)$Дозволяти функція,$f$ отримана з перекладу. З загальної властивості перетворення Фур'є: $$\mathcal{F}\left(f_{a, b}\right)(\xi, \eta)=e^{-2 \pi i(\xi a+\eta b)} \mathcal{F}(f)(\xi, \eta) . \nonumber$$ Отже, при перекладі поля$U_{0}$ інтенсивність в дальньому полі Фраунгофера не змінюється. На відміну від цього, за рахунок додаткового квадратичного фазового фактора в цілісному інтегралі Френеля інтенсивність поля Френеля в цілому$U_{0}$ змінюється при перекладі.
3. Припустимо,$U_{0}$ що поле відразу за$\mathcal{A}$ діаметром$D$ в непрозорому екрані. Потім можна показати, що точки$(x, y, z)$ спостереження, для яких дифракційні інтеграли Френеля і Фраунгофера є досить точними, задовольняють: $$\begin{aligned} &\frac{z}{\lambda}>\left(\frac{\max _{\left(x^{\prime}, y^{\prime}\right) \in \mathcal{A}} \sqrt{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}}{\lambda}\right)^{4 / 3} \text {, Fresnel } \\ &\frac{z}{\lambda}>\left(\frac{D}{\lambda}\right)^{2} \text {, Fraunhofer } \end{aligned} \nonumber$$ Припустимо, що$D=1 \mathrm{~mm}$ і довжина хвилі - зелене світло:$\lambda=550 \mathrm{~nm}$, то наближення Фраунгофера є точним, якщо$z>2 \mathrm{~m}$. Нерівність ($\PageIndex{6}$) достатня для того, щоб формула Френеля була точною, але це не завжди необхідно. Часто наближення Френеля вже є точним для менших відстаней поширення.
4. Точки спостереження, де можуть бути використані формули Фраунгофера, повинні в будь-якому випадку задовольняти: $$\frac{x}{z}<1, \quad \frac{y}{z}<1 . \nonumber$$ Коли просторова частота$x / z>1$,$k_{x}=\frac{2 \pi x}{z \lambda}>k$ пов'язана з цією точкою, відповідає хвилі, що зникає. Виникаюча хвиля, очевидно, не може сприяти дальньому полю Фраунгофера, оскільки вона експоненціально зменшується з відстанню$z$.
5. У будь-якому вираженні для оптичного поля завжди можна опустити фактори постійної фази, тобто загальної фази, яка не залежить від положення. Якщо хтось цікавиться лише полем у певних площинам$z=$ постійної, то фактор подібний також$\exp (i k z)$ може бути опущений. Крім того, в деяких випадках також опускається залежний від положення фазовий фактор перед дифракційними інтегралами Френеля і Фраунгофера, а саме коли цікавить лише інтенсивність. У вправах зазвичай згадується, що цей фактор може бути опущений: якщо це не заявлено, його слід зберегти у формулах.

Малюнок$\PageIndex{3}$: Демонстрація принципу невизначеності. Чим більш обмеженим$U(x, y)$ є, тим більший розкид$\mathcal{F}(U)\left(\frac{k_{x}}{2 \pi}, \frac{k_{y}}{2 \pi}\right)$.

Рисунок$\PageIndex{4}$: Приклад інтенсивності полів Френеля квадратної діафрагми, показаних у вигляді контурів і в поперечному перерізі для різних відстаней, які збільшуються від нижнього правого до верхнього лівого. Верхній лівий візерунок дорівнює візерунку Фраунгофера. $N_{F}=D^{2} / \lambda z$це число Френеля і$\lambda=600 \mathrm{~nm} .$

6.5.3 Приклади полів Френеля і Фраунгофера

Френеля наближення поля двох точкових джерел.

Розглянемо два точкових джерела в$\mathbf{r}_{s}^{+}=(a / 2,0,0)$ і$\mathbf{r}_{s}^{-}=(-a / 2,0,0)$. Поля кожного з них у точці$\mathbf{r}=(x, y, z)$ задаються значенням (5.6.2) $$U_{\pm}(\mathbf{r})=\frac{e^{i k\left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right|}}{\left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right|} \nonumber$$

Застосовуємо наближення Френеля для великих$z$: $$\begin{aligned} \left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right| &=z \sqrt{1+\frac{(x \mp a / 2)^{2}+y^{2}}{z^{2}}} \\ & \approx z+\frac{(x \mp a / 2)^{2}+y^{2}}{2 z} \\ &=z+\frac{x^{2}+y^{2}+a^{2} / 4}{2 z} \mp \frac{a x}{2 z} . \end{aligned} \nonumber$$

Звідси, $$U_{\pm}(\mathbf{r}) \approx \frac{e^{i k z}}{z} e^{i k \frac{x^{2}+y^{2}}{2 z}} e^{i k \frac{a^{2}}{8 z}} e^{\mp i k \frac{a x}{2 z}}, \nonumber$$ де в знаменнику ми замінили$\left|\mathbf{r}-\mathbf{r}_{s}^{\pm}\right|$ на$z$. Зверніть увагу, що наближення Фраунгофера становить$e^{i k a^{2} /(8 z)} \approx 1$ поки$e^{i k \frac{x^{2}+y^{2}}{2 z}}$ залишається фазовий фактор. Інтенсивність на екрані$z=$ константа загального поля дорівнює $$\begin{aligned} I_{\text {tot }}(\mathbf{r}) &=\left|U_{+}(\mathbf{r})+U_{-}(\mathbf{r})\right|^{2}=\frac{1}{z^{2}}\left|e^{-i k \frac{a x}{2 z}}+e^{i k \frac{a x}{2 z}}\right|^{2} \\ &=\frac{2}{z^{2}}\left[1+\cos \left(2 \pi \frac{a x}{\lambda z}\right)\right] \end{aligned} \nonumber$$

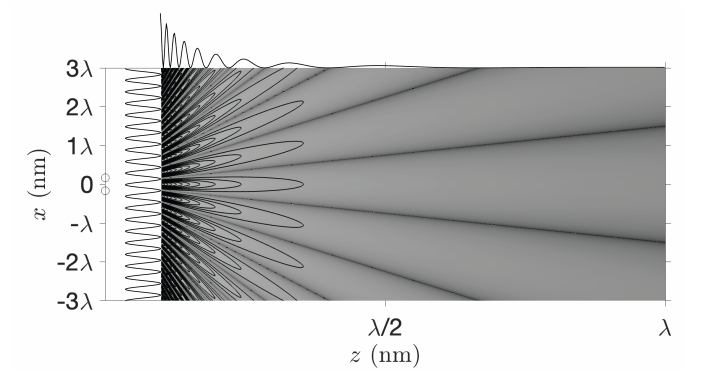
Видно, що інтенсивність є результатом інтерференції двох плоских хвиль:$\exp [\pm i k a x /(\lambda z)]$ і задається функцією косинуса (див. Рис.$\PageIndex{5}$). Зверніть увагу, що для двох точкових джерел картина інтенсивності однакова в наближенні Френеля та Фраунгофера. Однак це особливе для двох точкових джерел: коли розглядається більше двох точкових джерел, візерунки Френеля і Фраунгофера відрізняються. Візерунок інтенсивності не залежить від$y$ і зникає на рядках $$\frac{x}{z}=(2 m+1) \frac{\lambda}{2 a} \nonumber$$ і має максимуми на рядках $$\frac{x}{z}=m \frac{\lambda}{a}, \nonumber$$ для цілих чисел$m$.

Поле Фраунгофера прямокутної діафрагми в екрані.

Нехай екран буде$z=0$ і діафрагма буде дана$-a / 2<x<a / 2,-b / 2<y<b / 2$. Функція передачі$\tau(x, y)$ така: $$\tau(x, y)=1_{[-a / 2, a / 2]}(x) 1_{[-b / 2, b / 2]}(y), \nonumber$$ де $$1_{[-a / 2, a / 2]}(x)=\left\{\begin{array}{l} 1, \text { if }-\frac{a}{2} \leq x \leq \frac{a}{2}, \\ 0, \text { otherwise }, \end{array}\right. \nonumber$$ і аналогічно для$1_{[-b / 2, b / 2]}(y)$. Нехай щілина буде освітлена перпендикулярної падаючої площиною хвилею з одиничною амплітудою. Тоді поле відразу за екраном є: У $$U_{0}(x, y)=\tau(x, y)=1_{[-a / 2, a / 2]}(x) 1_{[-b / 2, b / 2]}(y), \nonumber$$ нас є $$\begin{aligned} \mathcal{F}\left(1_{[-a / 2, a / 2]}\right)(\xi) &=\int_{-a / 2}^{a / 2} e^{-2 \pi i \xi x} \mathrm{~d} x \\ &=\frac{e^{\pi i a \xi}-e^{-\pi i a \xi}}{2 \pi i \xi} \\ &=a \frac{\sin (\pi a \xi)}{\pi a \xi} \\ &=a \operatorname{sinc}(\pi a \xi), \end{aligned} \nonumber$$ де$\operatorname{sinc}(u)=\sin (u) / u$. Отже, $$\mathcal{F}\left(U_{0}\right)\left(\frac{x}{\lambda z}, \frac{y}{\lambda z}\right)=a b \operatorname{sinc}\left(\frac{\pi a x}{\lambda z}\right) \operatorname{sinc}\left(\frac{\pi b y}{\lambda z}\right) . \nonumber$$ дальнє поле Фраунгофера прямокутної діафрагми в площині на великій відстані$z$ виходить шляхом підстановки ($\PageIndex{25}$) в ($\PageIndex{9}$).

Малюнок$\PageIndex{5}$: Схема інтенсивності Фраунгофера з двох когерентних точкових джерел$200 \mathrm{~nm}$ один від одного (кіл), однакової сили для$\lambda=600 \mathrm{~nm}$.

Зауваження.

1. Перший нуль вздовж$x$ -напрямку від центру$x=0$ відбувається для $$x=\pm \frac{\lambda z}{a} . \nonumber$$ Відстань між першими двома нулями вздовж$x$$2 \lambda z / a$ -осі є і, таким чином, більше, коли ширина вздовж$x$ -direction діафрагма менше.
2. Нерівності ($\PageIndex{14}$) означають$a<\lambda$, що коли, шаблон далекого поля не має жодних нулів як функції$x$. Тоді важко або навіть неможливо вивести ширину$a$ з інтенсивності Фраунгофера. Це ілюстрація того, що інформація про розміри менше довжини хвилі не може поширюватися на дальнє поле.
3. Як показано на малюнку$\PageIndex{6}$, дифракційна картина Фраунгофера як функція кута дифракції є найвужчою у напрямку, в якому діафрагма є найширшою.

Малюнок$\PageIndex{6}$: Дифракційна картина Фраунгофера прямокутної діафрагми в непрозорому екрані. В) ширина отвору в$y$ -напрямку вдвічі більше, ніж в$x$ напрямку. В) ширина в$y$ -напрямку в 10 разів більше, ніж в$x$ -напрямку.

Періодичний масив щілин

Тепер ми можемо передбачити, як виглядатиме дифракційна картина серії щілин скінченної ширини. З малюнка Фраунгофера одного прямокутного отвору випливає, що, якщо сторони, паралельні напрямку, дуже довгі, дифракційна картина Фраунгофера як функція кута в цьому напрямку дуже вузька. На малюнку$\PageIndex{6}$ b показана дифракційна картина Фраунгофера прямокутної діафрагми, ширина якої у$y$ напрямку -10 разів більше, ніж у$x$ -напрямку. Потім дифракційна картина сильно концентрується уздовж$x$ -осі. Якщо розглядати лише шаблон Фраунгофера,$y / z=0$ поки ще розглядати його як функцію$x / z$, достатньо обчислити перетворення Фур'є лише щодо$x$. Потім проблема стає задачею дифракції для одновимірної щілини.

Розглянемо тепер масив таких прорізів, у яких довгі сторони паралельні$y$ -осі і відтепер нехтують$y$ -змінною. Припустимо,$W_{\text {slit }}(x)$ це блокова функція, що описує передавальну функцію однієї щілини. Визначаємо гребінь Дірака по $$\mathrm{II}_{\Delta}(x)=\sum_{m=-\infty}^{\infty} \delta(x-m \Delta) . \nonumber$$

Тоді передавальна функція нескінченного ряду щілин з скінченною шириною задається згорткою$\mathrm{II}_{\Delta}(x) * W_{\text {slit }}(x)$. Щоб число прорізів було кінцевим, множимо вираз на іншу блокову функцію$W_{\text {array }}(x)$ і отримуємо $$\tau(x)=\left(\mathrm{II}_{\Delta}(x) * W_{\text {slit }}(x)\right) W_{\text {array }}(x) . \nonumber$$

Дифракційна картина в далекому полі задається перетворенням Фур'є переданого ближнього поля. Якщо падаюче освітлення - це перпендикулярна плоска хвиля з одиничною амплітудою, передається ближнє поле просто$\tau(x)$. Використовуючи той факт, що згортки в реальному просторі відповідають добуткам у просторі Фур'є і навпаки, і використовуючи той факт, що $$\mathcal{F}\left\{\mathrm{W}_{\Delta}(x)\right\}=(1 / \Delta) \mathrm{W}_{1 / \Delta}(\xi), \nonumber$$ див. Додаток (Е.9) і (Е.10), знаходимо $$\mathcal{F}(\tau)=\frac{1}{\Delta}\left[\mathrm{W}_{1 / \Delta} \mathcal{F}\left(W_{\text {slit }}\right)\right] * \mathcal{F}\left(W_{\text {array }}\right). \nonumber$$

Якщо щілина має ширину$a$: $$\begin{aligned} \frac{1}{\Delta} \mathrm{I}_{1 / \Delta} \mathcal{F}\left(W_{\text {slit }}\right)(\xi) &=\frac{a}{\Delta} \sum_{m=-\infty}^{\infty} \delta\left(\xi-\frac{m}{\Delta}\right) \operatorname{sinc}(\pi a \xi) \\ &=\frac{a}{\Delta} \sum_{m=-\infty}^{\infty} \operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right) \delta\left(\xi-\frac{m}{\Delta}\right) . \end{aligned} \nonumber$$

Якщо загальна ширина масиву дорівнює$A$, то $$\mathcal{F}\left(W_{\text {array }}\right)(\xi)=A \operatorname{sinc}(\pi A \xi), \nonumber$$ і робимо висновок, що $$\mathcal{F}(\tau)(\xi)=\frac{a A}{\Delta} \sum_{m=-\infty}^{\infty} \operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right) \operatorname{sinc}\left(\pi A\left(\xi-\frac{m}{\Delta}\right)\right) . \nonumber$$

Поле Фраунгофера масиву щілин (без квадратичного фазового фактора): $$\mathcal{F}(\tau)\left(\frac{x}{\lambda z}\right)=\frac{a A}{\Delta} \sum_{m=-\infty}^{\infty} \operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right) \operatorname{sinc}\left(\pi A\left(\frac{x}{\lambda z}-\frac{m}{\Delta}\right)\right) . \nonumber$$

Для напрямків $$\frac{x}{z}=\theta_{m}=\frac{m \lambda}{\Delta}, \quad m=0, \pm 1, \pm 2, \ldots, \quad \text { diffraction orders } \nonumber$$ поле має локальні максимуми (піки). Ці напрямки називаються дифракційними порядками. Зверніть увагу, що, як пояснювалося вище, слід провести:$x / z<1$ в поле Fraunhofer far, яке встановлює обмеження на кількість дифрагованих ордерів, що відбуваються. Ця межа залежить від періоду і довжини хвилі і визначається: $$|m| \leq \Delta / \lambda . \nonumber$$

Отже, чим більше відношення періоду і довжини хвилі, тим більше порядку дифракції.

Ширина порядку дифракції задається шириною функції ($\PageIndex{31}$), тобто вона задається $$\Delta \theta=\frac{\lambda}{A}, \quad \text { angular width of a diffraction order. } \nonumber$$

Отже, чим більше$A$, тобто чим більше щілин в масиві, тим вужчі піки, в які дифрагується енергія.

Властивість ($\PageIndex{34}$), що кути дифракції порядків залежать від довжини хвилі, використовується для поділу довжин хвиль. Решітчасті спектрометри використовують періодичні структури, такі як цей масив щілин, щоб дуже точно відокремити та виміряти довжини хвиль. Наприклад, для решітки з 1000 періодів можна отримати дозвіл$\Delta \lambda / \lambda=10^{-3}$.

Амплітуди дифрагованих порядків: $$\operatorname{sinc}\left(m \pi \frac{a}{\Delta}\right), \nonumber$$ визначаються шириною щілин. Звідси огинаюча (тобто великі риси) дифракційної картини Фраунгофера визначається дрібномасштабними властивостями масиву, а саме шириною прорізів. Це проілюстровано на малюнку$\PageIndex{7}$. Зауваження. Періодичний ряд щілин є прикладом дифракційної решітки. Решітка - це періодична структура, тобто діелектрична проникність є періодичною функцією положення. Структури можуть бути періодичними в одному, двох і трьох напрямках. Кристал діє як тривимірна решітка, період якої є періодом кристала, тобто кілька Ангстрема. Електромагнітні хвилі довжиною хвилі, рівною одному Ангстрему або менше, називаються рентгенівськими променями. Коли промінь рентгенівських променів висвітлює кристал, детектор у далекому полі вимірює дифракційну картину Фраунгофера, задану інтенсивністю перетворення Фур'є заломленого ближнього поля. Ці дифракційні порядки кристалів для рентгенівських променів, де виявлені фон Лауе і використовуються для вивчення атомної структури кристалів.

Малюнок$\PageIndex{7}$: Ілюстрація дифракційного малюнка серії з чотирьох прорізів.