2.6: Гаусова геометрична оптика
- Page ID
- 78782
Вище ми бачили, що за допомогою лінз або дзеркал, які мають поверхні, що є конічними перерізами, ми можемо ідеально зобразити певну пару точок, але для інших точок зображення взагалі не є ідеальним. Недосконалості викликані променями, які роблять більші кути з оптичною віссю, тобто з віссю симетрії системи. Промені, для яких ці кути невеликі, називаються параксіальними променями. Оскільки для параксиальних променів кути падіння і пропускання на поверхнях лінз невеликі, синуси кутів в законі Снелла замінюються самими кутами:
\[n_{i}θ_{i}=n_{t}θ_{t}. \tag{paraxial space rays space only} \]
Таке наближення значно спрощує розрахунки. Коли розглядаються лише параксіальні промені, можна замінити будь-яку заломлюючу поверхню сферою з тією ж кривизною в її вершині. Для параксиальних променів похибки, викликані заміною загальної поверхні сферою, мають другий порядок і, отже, незначні. Сферичні поверхні не тільки більш прості у виведенні, але вони також набагато простіші у виготовленні. Звідси в оптичній промисловості сферичних поверхонь використовується дуже багато. Щоб зменшити помилки візуалізації, спричинені непараксиальними променями, застосовується дві стратегії:
- додавання більш сферичних поверхонь
- заміна однієї зі сферичних поверхонь (зазвичай останньої перед простором зображення) на несферу.
У гауссовой геометричній оптиці розглядаються лише параксіальні промені та сферичні поверхні. У геометричній оптиці Гаусса кожна точка має ідеальне зображення.
2.5.1 Гаусова візуалізація єдиною сферичною поверхнею
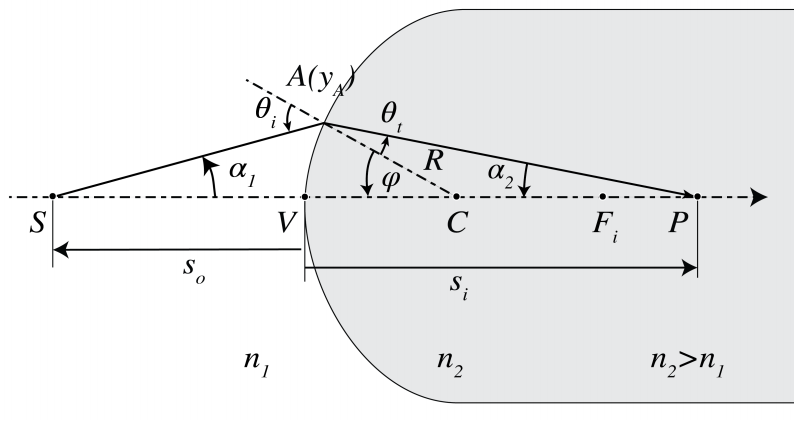
Спочатку ми покажемо, що в межах гаусової оптики єдина сферична поверхня між двома середовищами з показниками заломлення n 1 < n 2 зображає всі точки ідеально (рис.\(\PageIndex{1}\)). Сфера має радіус R і центр C, який знаходиться всередині середовища 2. Розглядаємо точковий об'єкт S зліва від поверхні. Промінь проводимо від S перпендикулярно до поверхні. Точка перетину дорівнює V. Оскільки для цього променя кут падіння з локальною нормаллю на поверхню зникає, промінь продовжується у друге середовище без заломлення і проходить через центр С сфери. Далі малюємо промінь, який потрапляє на сферичну поверхню в деякій точці А і малюємо заломлений промінь в середовищі 2, використовуючи закон Снелла в параксіальній формі (\(\PageIndex{1}\)) (зверніть увагу, що кути падіння і передачі повинні вимірюватися щодо локальної нормалі при А, тобто по відношенню до СА). Ми припустимо, що цей промінь перетинає перший промінь у точці P. Ми покажемо, що в межах наближення гаусової геометричної оптики всі промені з S проходять через P. Крім того, відносно системи координат (y, z) з початком у V, вісь z, що вказує від V до C, а вісь y позитивна вгору як показано на малюнку\(\PageIndex{1}\), ми маємо:
\[-\dfrac{n_{1}}{s_{0}}+\dfrac{n_{2}}{s_{i}}=\dfrac{n_{2}-n_{1}}{R}. \nonumber \]
де s 0 і s i є z- координатами S і P відповідно (отже, s 0 0 < 0 and si > на рис.\(\PageIndex{1}\)).
Доказ.
(Примітка: доказ не є частиною іспиту). Досить показати, що P не залежить від променя, тобто від A. Ми зробимо це, висловивши s i в s o і показавши, що результат не залежить від A. Нехай α 1 і α 2 - кути променів SA і AP з віссю z, як показано на малюнку\(\PageIndex{1}\). Нехай θ i - кут падіння променя SA з локальним нормальним CA на поверхню, а θ t - кут заломлення. Розглядаючи кути в SCA, ми знаходимо
\[θ_{i}=α_{1}+ϕ. \nonumber \]
Аналогічно, з ∆CPA знаходимо
\[θ_{t}=-α_{2}+ϕ. \nonumber \]
Шляхом підміни в параксиальну версію закону Снелла (\(\PageIndex{1}\)), отримуємо
\[n_{1}α_{1}+n_{2}α_{2}=(n_{2}-n_{1})ϕ. \nonumber \]
Нехай y A і z A будуть координатами точки A. Оскільки s o < 0 і s i > 0 ми маємо
\[α_{1}≈tan(α_{1})=\dfrac{y_{A}}{z_{A}-s_{o}},α_{2}≈tan(α_{2})=\dfrac{y_{A}}{s_{i}-z_{A}}. \nonumber \]
Крім того,
\[ϕ≈\sin ϕ≈\dfrac{y_{A}}{R}. \nonumber \]
що мало для параксиальних променів. Отже,
\[z_{A}=R-R\cos ϕ=R-R(1-\dfrac{ϕ^2}{2})=\dfrac{R}{2}ϕ^2≈0, \nonumber \]
тому що це другий порядок у y A і тому нехтується в параксиальному наближенні. Потім, (\(\PageIndex{6}\)стає
\[α_{1}=-\dfrac{y_{A}}{s_{o}},α_{2}=\dfrac{y_{A}}{s_{i}}. \nonumber \]
Підставляючи (\(\PageIndex{9}\)і (\(\PageIndex{7}\)в (\(\PageIndex{5}\)знаходимо − (n 1 /s o) y A + (n 2 /z i) y A = [(n 2 − n 1) /R] y A, або −n 1 /s o +n 2 /z i =( n 2 − n 1) /R, що є еквалайзером. (\(\PageIndex{2}\). Це означає\(s_i\), що і, отже\(P\), не залежить від y A, тобто від обраного променя. Тому P є ідеальним зображенням в межах наближення гаусової геометричної оптики.
При s i → ∞ промінь після заломлення паралельний осі z і отримуємо так → −n 1 R/ (n 2 − n 1). Точка об'єкта, для якої промені в середовищі 2 паралельні осі z, називається першою фокусною точкою або об'єктною фокусною точкою F o, Її z-координата дорівнює:
\[f_{o}=- \dfrac{ n_{1}R }{ n_{2} -n_{1} }. \nonumber \]
Незважаючи на те, що це координата і, отже, має знак, його ще називають передньою фокусною відстанню або фокусною відстанню об'єкта.
Коли s o → −∞, падаючий промінь паралельний осі z в середовищі 1, а відповідна точка зображення F i називається другою фокусною точкою або фокусною точкою зображення. Його z-координата задається:
\[f_{i}=\dfrac{ n_{2}R }{ n_{2} -n_{1} }, \nonumber \]
і його також називають другою фокусною відстанню або фокусною відстанню зображення. З (\(\PageIndex{11}\)) і (\(\PageIndex{10}\)), (\(\PageIndex{2}\)) можна переписати як:
\[- \dfrac{ n_{1}}{ s_{o} }+ \dfrac{ n_{2}}{ s_{i} } = \dfrac{ n_{2}}{ f_{i} } = -\dfrac{ n_{1}}{ f_{o} }. \nonumber \]
Прийнявши конвенцію про знак, перераховану в таблиці\(\PageIndex{1}\) нижче, виявляється, що (\(\PageIndex{2}\)) тримається загалом. Наприклад, коли точка S знаходиться між передньою фокусною точкою і вершиною V так, що f o < s o < 0, промені від S настільки сильно розходяться, що заломлення недостатньо для отримання точки зображення в середовищі 2. Замість цього існує розбіжний пучок променів у середовищі 2, який для спостерігача в середовищі 2, здається, походить з точки P в середовищі 1 з z-координатою si, отже si < 0, у згоді з тим, що P тепер зліва від V. Точка P називається віртуальним зображенням, тому що вона не відповідає фактична концентрація світлової енергії в просторі. Коли s i > 0 існує концентрація світлової енергії в P, яка, отже, називається реальним зображенням.

| кількість | позитивний | негативний |
|---|---|---|
| s o, f o, s i, f i | відповідна точка знаходиться праворуч від вершини | відповідна точка ліворуч від вершини |
| Р | центр кривизни праворуч від вершини | центр кривизни зліва від вершини |
| α (проникливий кут променя) | якщо обертання проти годинникової стрілки над α робить промінь паралельним осі z | якщо обертання за годинниковою стрілкою над α робить промінь паралельним осі z |
| Реф. індекс в навколишньому середовищі дзеркала | перед роздумом | після роздумів |
Якщо\(n_1 > n_2\) або\(R < 0\) (тобто поверхня увігнута, коли видно зліва від вершини), права сторона (\(\PageIndex{2}\)) негативна:
\[\dfrac{n_{2}-n_{1}}{R}<0. \nonumber \]
Світлові промені, що падають зліва, потім заломлюються від осі z і падаючі промені, паралельні осі z, заломлюються таким чином, що вони ніколи не перетинаються вісь z в середовищі 2. Натомість вони, здається, випромінюються точкою в середовищі 1. Як показано на малюнку\(\PageIndex{2}\), друга фокусна точка, таким чином, віртуальна з негативною фокусною відстанню, заданою:
\[f_{i}=\dfrac{n_{2}R}{n_{2}-n_{1}}<0. \nonumber \]
Крім того, f o > 0 і падаючий промінь, який після заломлення паралельний осі z в середовищі 2 здається, що спостерігач у середовищі 1 сходиться до точки в середовищі 2. Отже, перший фокусний пункт також віртуальний: f o > 0. Коли (\(\PageIndex{12}\)) утримує, для всіх точок об'єкта S перед об'єктивом (s o < 0) точка зображення завжди віртуальна. Насправді, si, як дано (\(\PageIndex{2}\)), то завжди негативний.
2.5.2 Променеві вектори та матриці променів
У геометричній оптиці зручно використовувати вектори променів і променеві матриці. У будь-якій площині, перпендикулярній осі z, промінь визначається y-координатою точки перетину променя з площиною і гострим кутом α променя з віссю z. Тут y > 0, коли точка перетину знаходиться над віссю z і y < 0 інакше. Визначаємо вектор променя
\[\dbinom{nα}{y}, \nonumber \]
де n - місцевий показник заломлення. Зручним виявляється визначення з показником заломлення як фактора в першому елементі вектора променя. Гострий кут α має знак згідно з конвенцією в табл\(\PageIndex{1}\).
Вектори променів променя в будь-яких двох площинях z = z 1, z = z 2, з z 2 > z 1 пов'язані так званою матрицею променів:
\[\dbinom{n_{2}α_{2}}{y_{2}}=M\dbinom{n_{1}α_{1}}{y_{1}}. \nonumber \]
де
\[M=\begin{pmatrix} A & B \\ C & D \end{pmatrix}. \nonumber \]
Елементи матриці M залежать від оптичних складових і матеріалів між площинами z = z 1 і z = z 2.
Як приклад розглянемо матрицю променя, яка пов'язує вектор променя в площині безпосередньо перед сферичною поверхнею на малюнку\(\PageIndex{2}\) з відповідним вектором променя в площині безпосередньо за цією поверхнею. Використовуючи (\(\PageIndex{5}\)) і (\(\PageIndex{7}\)) слід
\[n_{1}α_{1}-n_{2}α_{2}=\dfrac{(n_{2}-n_{1})y_{1}}{R}, \nonumber \]
де ми замінили α 2 на −α 2 in (\(\PageIndex{5}\)), тому що згідно зі знаковою конвенцією кут α 2 на малюнку\(\PageIndex{1}\) слід приймати негативним. Тому що крім y 2 = y 1, ми робимо висновок
\[\dbinom{n_{2}α_{2}}{y_{2}}=\dbinom{n_{1}α_{1}-\dfrac{(n_{2}-n_{1})y_{1}}{R}}{y_{1}}=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix}\dbinom{n_{1}α_{1}}{y_{1}},spherical\space surface, \nonumber \]
де
\[P=\dfrac{n_{2}-n_{1}}{R}, \nonumber \]
називається силою поверхні.
Для сферичного дзеркала з радіусом кривизни R ми бачимо, що
\[α_{1}=θ_{i} − ϕ, \nonumber \]
\[α_{2}=-θ_{r} − ϕ, \nonumber \]
де ми беремо знак умовності для кутів до уваги. Тому що θ r = θ i ми знаходимо
\[α_{2}=-α_{1}+2ϕ=-α_{1}+2\dfrac{y_{1}}{R}, \nonumber \]
де ми використовували (\(\PageIndex{7}\)) з y A = y 1. Як зазначено в таблиці\(\PageIndex{1}\), показник заломлення після відображення повинен бути обраний негативним. Це означає, що для променів, які поширюються справа наліво, показник заломлення в векторі променя слід вибирати негативний. Отже,
\[n_{2}α_{2}=-n_{1}α_{2}= n_{1}α_{1} -2n_{1}\dfrac{y_{1}}{R}. \nonumber \]
Тоді
\[\dbinom{n_{2}α_{2}}{y_{2}}=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix}\dbinom{n_{1}α_{1}}{y_{1}},spherical\space reflector, \nonumber \]
де
\[P=\dfrac{2n_{1}}{R} \nonumber \]
це сила дзеркала. Зроблено висновок, що матриця променя для відображення сферичним дзеркалом така ж, як і для заломлення сферичною поверхнею, за умови, що n 2 замінено на −n 1. Коли промінь поширюється справа наліво, показник заломлення всіх середовищ і інтерфейсів, через які промінь поширюється, і при якому він заломлюється, повинен мати негативний показник заломлення. Після того як промінь відбився вдруге, за рахунок чого він знову поширюється зліва направо, всі показники заломлення знову повинні бути позитивними. Таким чином матричний метод може бути застосований до оптичних систем, що складаються як з заломлюючих елементів, таких як лінзи, так і відображають елементів.
Нарешті ми розглянемо випадок, що між двома площинами є однорідний матеріал з показником заломлення n, у цьому випадку α 2 = α 1 і y 2 = y 1 + α 1 (z 2 − z 1), отже
\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{z_{2}-z_{1}}{n} & 1 \end{pmatrix},homogeneous\space space. \nonumber \]
Для двох площин, між якими є ряд оптичних компонентів, можливо розділених областями з однорідним матеріалом (наприклад, повітрям), матрицю променя можна отримати шляхом множення матриць окремих компонентів та однорідних областей. Порядок множення матриць такий, що крайня права матриця відповідає першому компоненту, який зустрічається при поширенні, і так далі.
Слід зазначити, що промені, що розглядаються в наближенні матриці променя, залишаються в одній площині, а саме площині через промінь і вісь z. Ці промені називаються меридіональними променями. Розглядаючи лише меридіональні промені, візуалізація оптичними системами обмежується двома вимірами. Немеридіональні промені називаються косими променями. Перекісні промені не проходять через оптичну вісь і вони не розглядаються в параксіальної теорії.
2.5.3 Матриця об'єктива
Наносимо променеві матриці до лінзи. \(\PageIndex{4}\)На малюнку зображена лінза з двома сферичними поверхнями. Показник заломлення об'єктива дорівнює n l, а показник навколишнього середовища - n m, а відстань між вершинами - d Спочатку ми виведемо матрицю, яка відображає вектор променя в площині безпосередньо перед лінзою до тієї, що в площині негайно. за об'єктивом. Нехай
\[\dbinom{n_{m}α_{1}}{y_{1}}and\dbinom{n_{m}α_{2}}{y_{2}} \nonumber \]
бути двома векторами в двох площинами, які відповідають одному і тому ж променю. Промінь спочатку заломлюється сферичною поверхнею радіусом R 1 і центром C 1. Використовуючи (\(\PageIndex{25}\)) і (\(\PageIndex{20}\)) випливає, що матриця між векторами променів безпосередньо перед і безпосередньо за сферичною поверхнею з радіусом R 1 і центром C 1 задається
\[M_{1}=\begin{pmatrix} 1 & -\dfrac{ n_{l} - n_{m} }{R_{1}} \\ 0 & 1 \end{pmatrix} \nonumber \]
Потім промінь поширюється на відстань d через матеріал, з якого виготовлена лінза. Матриця, яка відображає вектори променів з площини всередині лінзи безпосередньо за лівою сферичною поверхнею на вектор променя в площині безпосередньо перед правою сферичною поверхнею випливає з (\(\PageIndex{27}\)):
\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{d}{n_{l}} & 1 \end{pmatrix}. \nonumber \]
Нарешті, матриця, яка відображає вектори променів від площини в лінзі безпосередньо перед другою сферичною поверхнею до векторів в площині безпосередньо за нею
\[M_{1}=\begin{pmatrix} 1 & -\dfrac{ n_{m} - n_{l} }{R_{2}} \\ 0 & 1 \end{pmatrix}. \nonumber \]
Звідси матриця, яка відображає вектори променів у площині безпосередньо перед лінзою до векторів променів у площині безпосередньо за лінзою, задається матричним добутком:
\[M=M_{3}M_{2}M_{1}=\begin{pmatrix} 1-\dfrac{d}{n_{l}}P_{2} & -P_{1}-P_{2}+\dfrac{d}{n_{l}}P_{1}P_{2} \\ \dfrac{d}{n_{l}} & 1-\dfrac{d}{n_{l}}P_{1} \end{pmatrix},lens, \nonumber \]
де
\[P_{1}=\dfrac{ n_{l} - n_{m} }{R_{1}},P_{2}=\dfrac{ n_{m} - n_{l} }{R_{2}}. \nonumber \]
Кількість
\[P=P_{1}+P_{2}-\dfrac{d}{n_{l}}P_{1}P_{2} \nonumber \]
називається потужність об'єктива. Він має розмір 1/довжину і задається в діоптріях (D), де 1 D = m −1. Харчування може бути позитивним і негативним. Вісь z є віссю симетрії і називається оптичною віссю. Простір ліворуч від об'єктива називається об'єктним простором, а праворуч від об'єктива називається простором зображення.

2.5.4 Фокусування за допомогою тонкої лінзи
Для тонкої лінзи вершини V 1 і V 2 збігаються і d = 0, отже (\(\PageIndex{34}\)) стає
\[M=\begin{pmatrix} 1 & -P \\ 0 & 1 \end{pmatrix},thin\space lens, \nonumber \]
де Р = П 1 + Р 2, причому Р 1 і Р 2 дано (\(\PageIndex{35}\)). Походження системи координат вибирається в загальній вершині V 1 = V 2. Для променя, що виникає в просторі зображення на висоті y 2 і паралельно оптичній осі: α 2 = 0, маємо y 1 = y 2 і
\[n_{m} α _{1}=P_{y}. \nonumber \]
Якщо потужність додатна: P > 0, кут α1 має той же знак, що і y 1, що означає, що промінь у просторі об'єкта перетинав оптичну вісь в точці F o з z-координатою: z = f o задовольняє
\[\dfrac{1}{f_{o}}=\dfrac{α _{1}}{y _{1}} = \dfrac{n_{m}}{P}=\dfrac{n_{l}-n_{m}}{n_{m}}(\dfrac{1}{R_{1}}-\dfrac{1}{R_{2}}). \nonumber \]
Точка Fo називається першою фокусною точкою або об'єктною фокусною точкою.
Аналогічно, розглядаючи промінь в середовищі 1, який паралельний оптичній осі (α 1 = 0) і на висоті y 1, отримуємо n m α 2 = −P y 1 і y 2 = y 1. Отже, коли P > 0, кут α 2 променя має знак протилежний y 2, і тому промінь у просторі зображення згинається назад до оптичної осі, отримуючи другу фокусну точку або фокусну точку зображення F i. Його z-координата f i задовольняє:
\[\dfrac{1}{f_{i}}=-\dfrac{α _{2}}{y _{2}} = -\dfrac{n_{m}}{P}=-\dfrac{1}{f_{o}}. \nonumber \]
Коли потужність P лінзи позитивна, f i = −f o > 0, що означає, що перша і друга фокусні точки знаходяться в об'єкті та просторі зображення відповідно. Лінза з позитивною силою називається збіжною або позитивною.
Лінза з негативною силою називається дивергентною і має f i = −f o < 0. Потім падаючі промені, паралельні оптичній осі, заломлюються від оптичної осі і, здається, виходять з точки перед лінзою з z-координатою f i < 0. Отже, друга фокусна точка не відповідає місцю, де є фактична концентрація інтенсивності світла, а отже, вона віртуальна. Перша фокусна точка - це віртуальна об'єктна точка, тому що тільки для пучка падаючих променів, які сходяться до певної точки за лінзою, негативна заломлення може дати пучок променів, які всі паралельні оптичній осі.
З отриманими результатами для фокусних координат ми можемо переписати матрицю лінзи тонкої лінзи альтернативно як
\[M=\begin{pmatrix} 1 & -\dfrac{n_{m}}{f_{i}} \\ 0 & 1 \end{pmatrix},thin\space lens. \nonumber \]
2.5.5 Зображення за допомогою тонкої лінзи
Розглянемо спочатку загальну матрицю променів (\(\PageIndex{16}\)), (\(\PageIndex{17}\)) між двома площинами z = z 1 і z = z 2 і задаємо наступне питання: які властивості матриці променів такі, що дві площини є зображеннями один одного, або (як це ще називають) є сполученими один одного ? Очевидно, щоб ці площини були зображенням один одного, ми повинні мати, що для кожної точки координати y 1 в площині z = z 1, є точка з координатою y 2 в площині z = z 2 така, що будь-який промінь через (y 1, z 1) (в межах деяких конус променів) буде проходити через точку (y 2, z 2). Отже, для будь-якого кута α 1 (в деякому інтервалі кутів) існує кут α 2 такий, що (\(\PageIndex{16}\)) є дійсним. Це означає, що для будь-якого y 1 існує y 2 такий, що для всіх кутів α 1:
\[y _{2}=Cn_{1}α _{1}+Dy _{1}, \nonumber \]
Для цього потрібно, щоб
\[C = 0, condition\space for\space imaging. \nonumber \]
Співвідношення y 2 і y 1 дає збільшення. Звідси
\[\dfrac{y _{2}}{y _{1}}=D, \nonumber \]
- збільшення зображення (ця величина має знак).
Для визначення зображення точки тонкою лінзою спочатку виведемо матрицю променя між площинами z = z 1 < 0 і z = z 2 > 0 з тонкою лінзою між ними з вершиною на початку. Ця матриця є добутком матриці для поширення від z = z 1 до площини відразу перед лінзою, матриці тонкої лінзи і матриці для поширення від площини відразу за лінзою до площини z = z 2:
\[M=\begin{pmatrix} 1 & 0 \\ \dfrac{z _{2}}{n _{m}} & 1 \end{pmatrix}\begin{pmatrix} 1 & -\dfrac{n _{m}}{f_{i}} \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ -\dfrac{z _{1}}{n _{m}} & 1 \end{pmatrix}=\begin{pmatrix} 1+\dfrac{z _{1}}{f_{i}} & -\dfrac{n _{m}}{f_{i}} \\ -\dfrac{z _{1}}{n _{m}}+\dfrac{z _{2}}{n _{m}}+\dfrac{z _{1}z _{2}}{n _{m}f_{i}} & 1-\dfrac{z _{2}}{f _{i}} \end{pmatrix} \nonumber \]
Умова візуалізації (\(\PageIndex{41}\)) має на увазі:
\[-\dfrac{1}{s _{o}}+\dfrac{1}{s _{i}}=\dfrac{1}{f _{i}},Lensmaker's\space Formula. \nonumber \]
де ми написали s o = z 1 і s i = z 2 для z-координат об'єкта і зображення. Оскільки для матриці тонкої лінзи (\(\PageIndex{43}\)): D = 1− z 2 /f i, за допомогою (\(\PageIndex{44}\)) випливає, що збільшення (\(\PageIndex{42}\)) задається
\[M=\dfrac{y _{i}}{y _{o}}=1-\dfrac{s _{i}}{f _{i}}=\dfrac{s _{i}}{s _{o}}, \nonumber \]
де ми написали зараз y o і y i замість y 1 і y 2 відповідно.
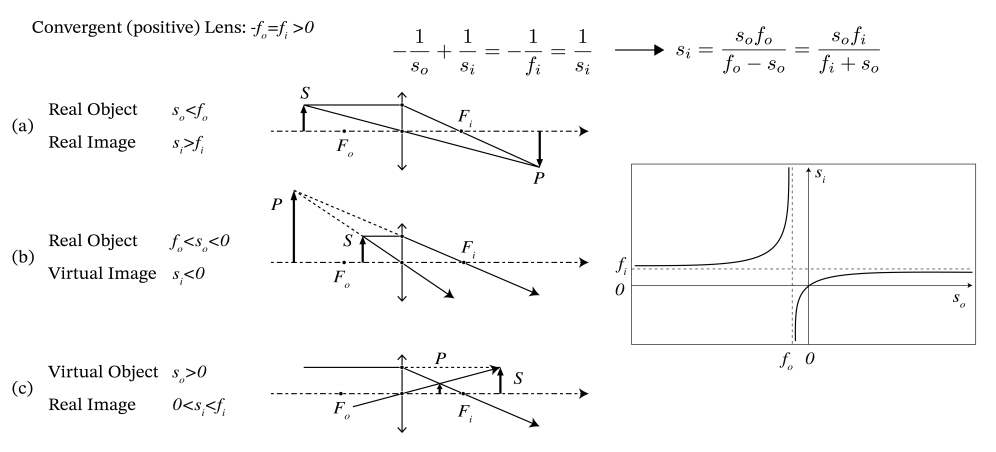
Для позитивної лінзи: f i > 0 і, отже, (\(\PageIndex{44}\)) означає, що s i > 0 передбачено |s o | < f i = |f o |, що означає, що зображення за допомогою конвергентної лінзи є реальним, якщо об'єкт знаходиться далі від об'єктива, ніж перша фокусна точка F o. Випадок s o > 0 відповідає віртуальному об'єкту, тобто випадку збігається пучка падаючих променів, які для спостерігача в об'єктному просторі, здається, сходяться до точки на відстані так позаду лінзи. Потім конвергентна лінза (f i > 0) зробить зображення між об'єктивом і другою фокусною точкою. На відміну від цього, розбіжна лінза (f i < 0) може перетворити інцидент-сходяться пучок в реальне зображення тільки в тому випадку, якщо віртуальна точка об'єкта знаходиться між об'єктивом і фокусною точкою. Якщо точка віртуального об'єкта має більшу відстань до лінзи, зближення падаючого пучка занадто слабке, і розбіжна лінза потім заломлює цей пучок в розходяться пучок променів з вершиною в віртуальній точці зображення перед лінзою (s i < 0).
Також можна сконструювати зображення за допомогою лінійки. Розглянемо візуалізацію скінченного об'єкта S 1 S 2, як показано на малюнку\(\PageIndex{4}\). Нехай y o - y-координата S 2. У нас є y o > 0, коли об'єкт знаходиться над оптичною віссю. Намалюйте промінь через фокусну точку F o в просторі об'єкта і промінь через центр V лінзи. Перший промінь стає паралельним в просторі зображення. Остання перетинає обидві поверхні лінзи майже в їх (майже збігаються) вершині і тому заломлення протилежно на обох поверхнях і промінь виходить з лінзи паралельно її напрямку падіння. Крім того, його бічним зміщенням можна знехтувати, оскільки лінза тонка. Отже, промінь через центр лінзи не заломлюється. Перетин в просторі зображення двох променів дає розташування точки зображення P 2 з S 2. Зображення є реальним, якщо перетин відбувається в просторі зображення і є віртуальним в іншому випадку. Для випадку збіжною лінзи з реальним об'єктом з y o > 0, як показано на малюнку\(\PageIndex{4}\), з аналогічних трикутників Δ AVF i і ∆P 2 P 1 F i випливає, що
\[\dfrac{y _{o}}{|y _{i}|}=\dfrac{f _{i}}{s _{i}-f _{i}}, \nonumber \]
де ми використовували |f o | = f i. З аналогічних трикутників Δ S 2 S 1 F o і θ BVF o:
\[\dfrac{|y _{i}|}{y _{o}}=\dfrac{f _{i}}{f _{o}-s _{o}}. \nonumber \]
(Абсолютне значення y i береться тому, що згідно з нашим знаком конвенції y i на малюнку\(\PageIndex{4}\) є від'ємним, тоді як (\(\PageIndex{44}\)) - відношення довжин). Помноживши ці два рівняння, отримаємо ньютонівську форму рівняння лінзи:
\[x _{o}x _{i}=-f _{i}^2=-f _{o}^2, \nonumber \]
де x o та x i - координати об'єкта та зображення відносно координат першої та другої фокусної точки відповідно:
\[x _{o}=s _{o}-f _{o},x _{i}=s _{i}-f _{i}. \nonumber \]

Отже x o є негативним, якщо об'єкт t ліворуч від F o і x i є позитивним, якщо зображення знаходиться праворуч від F i.
Поперечне збільшення
\[M=\dfrac{y _{i}}{y _{o}}=\dfrac{s _{i}}{s _{o}}= -\dfrac{x _{i}}{f _{i}} , \nonumber \]
де друга ідентичність випливає з розгляду аналогічних трикутників ΔP 2 P 1 F i та ΔAVF i на рис\(\PageIndex{4}\). Позитивний М означає, що зображення прямостояче, негативний M означає, що зображення перевернуто (як це завжди буває для однієї лінзи).
Всі рівняння також дійсні для тонких негативних лінз і для віртуальних об'єктів і зображень. Деякі приклади реальних і віртуальних об'єктів і точок зображення для позитивної і негативної лінзи наведені на рис. \(\PageIndex{5}\)і\(\PageIndex{6}\).
2.5.6 Дві тонкі лінзи
Візуалізація двома тонкими лінзами L 1 і L 2 може бути легко отримана конструкцією. Ми просто будуємо зображення, отримане першою лінзою так, ніби другої лінзи не було, і використовуємо це зображення як (можливо, віртуальний) об'єкт для другої лінзи. На малюнку показано\(\PageIndex{7}\) приклад, де відстань між лінзами більше суми їх фокусних відстаней. Спочатку побудовано зображення P 'з S, отримане за допомогою L 1 так, ніби L 2 не було. Побудовано проміжне зображення P' за рахунок об'єктива L 1 за допомогою променів 2 і 3. P 1 - це реальне зображення об'єктива L 1, який також є реальним об'єктом для об'єктива L 2. Промінь 3 паралельний оптичній осі між двома лінзами і таким чином заломлюється лінзою L2 через її задню фокусну точку F 2i. Промінь 4 - це промінь від P1 через центр лінзи L 2. Точка зображення Р - це перетин променя 3 і 4.
У випадку з малюнком\(\PageIndex{8}\) відстань d між двома позитивними лінзами менше, ніж їх фокусні відстані. Проміжне зображення P' являє собою реальне зображення для L 1, отримане у вигляді перетину променів 2 і 3, що проходять через об'єкт і фокусних точок зображення F 1o і F 1i об'єктива L 1. P 'тепер віртуальна точка об'єкта для об'єктива L 2. Щоб знайти його зображення по L 2, проведіть промінь 4 від P 'через центр лінзи L 2 назад до S (цей промінь заломлюється лінзою L 1, але не L 2) і намалюйте промінь 3 як заломлений лінзою L 2. Так як промінь 3 паралельний оптичній осі між лінзами, то він проходить через задню фокусну точку F 2i об'єктива L 2. Точка перетину променя 3 і 4 - кінцева точка зображення P.



Легко висловити z-координату s i щодо системи координат з початком у вершині L 2 кінцевої точки зображення, в z-компоненті s o щодо початку у вершині лінзи L 1 точки об'єкта. Ми використовуємо формулу Lensmaker для кожного об'єктива, дбаючи про те, щоб у кожному випадку використовувалася належна локальна система координат. Проміжне зображення P' за рахунок об'єктива L 1 має z-координату s 1i щодо системи координат з початком у вершині V 1, яка задовольняє:
\[\dfrac{1}{s_{o}}+\dfrac{1}{s_{1i}}=\dfrac{1}{f_{1i}}. \nonumber \]
P' є об'єктом для об'єктива L 2 з z-координатою відносно системи координат з початком V 2 задано: s 2o = s 1i − d, де d - відстань між лінзами. Отже, з s i = s 2i Формула об'єктива L 2 має на увазі:
\[-\dfrac{1}{s_{1i}-d}+\dfrac{1}{s_{i}}= \dfrac{1}{f_{2i}}. \nonumber \]
\(\PageIndex{51}\)Розв'язавши () для s 1i і підставивши результат в (\(\PageIndex{52}\)), знаходимо
\[s_{i}=\dfrac{-df_{1i} f_{2i}+ f_{2i}( f_{1i} -d)s_{o} }{ f_{1i}( f_{2i} -d) +( f_{1i}+ f_{2i} -d)s_{o} },two\space thin\space lenses. \nonumber \]
Беручи межу s o → −∞, отримаємо z-координату f i фокусної точки зображення двох об'єктивів, тоді як s i → ∞ дає z-координату f o фокусної точки об'єкта:
\[f_{i}=\dfrac{( f_{1i} -d) f_{2i} }{ f_{1i}+ f_{2i} -d}, \nonumber \]
\[f_{o}=-\dfrac{( f_{2i} -d) f_{1i} }{ f_{1i}+ f_{2i} -d}, \nonumber \]
За винятком випадків, коли показники заломлення носія до і після лінзи різні, фокусні відстані об'єкта та зображення тонкої лінзи однакові. Однак, як випливає з похідної формули для оптичної системи з двома лінзами, фокусні відстані об'єкта та зображення взагалі відрізняються, коли є кілька лінз.
Побудуючи з використанням проміжного зображення, зрозуміло, що збільшення дволінзової системи є продуктом збільшення двох лінз:
\[M=M_{1}M_{2}. \nonumber \]
Зауваження
1. При f 1i + f 2i = d фокусні точки знаходяться на нескінченності. Така система називається телецентричної.
2. У межі, де лінзи знаходяться дуже близько один до одного: d → 0, (\(\PageIndex{53}\)) стає
\[-\dfrac{1}{s_{o}}+\dfrac{1}{s_{i}}= \dfrac{1}{f_{1i}}+ \dfrac{1}{f_{2i}}. \nonumber \]
Фокусна відстань if системи двох контактних лінз задовольняє таким чином:
\[\dfrac{1}{f_{i}}=\dfrac{1}{f_{1i}}+\dfrac{1}{f_{2i}}. \nonumber \]
Дві позитивні лінзи в тісному контакті примушують один одного, тобто друга позитивна лінза робить збіжність першої лінзи сильнішою. Аналогічно дві негативні лінзи при контакті роблять більш сильно негативну систему. Те ж саме стосується більш ніж двох лінз, що знаходяться в тісному контакті.
3. Хоча для двох лінз координата зображення все ще може бути виражена відносно легко на відстані об'єкта, для систем з більшою кількістю лінз, що знаходять загальну матрицю променів, а потім використовують умову зображення (\(\PageIndex{41}\)) є набагато кращою стратегією.
2.5.7 Товста лінза
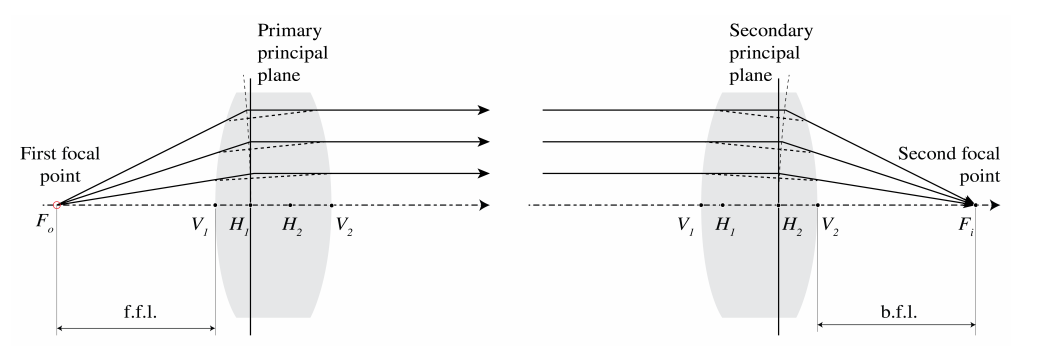
Зліва на малюнку\(\PageIndex{9}\) показана товста лінза. Перша фокусна точка визначається як точка, промені якої заломлюються таким чином, що з'являються промені паралельні оптичній осі. Розширюючи падаючі і виникають промені прямими відрізками, точки перетину виявляються на криволінійній поверхні, яка близько до оптичної осі, тобто в параксиальному наближенні, знаходиться в хорошому наближенні площину, перпендикулярну оптичній осі. Ця площина називається первинною основною площиною і її перетин з оптичною віссю називається первинною головною точкою H 1. Розглядаючи падаючі промені, які паралельні оптичній осі і, отже, зосереджені в задній фокусній точці, вторинна основна площина і вторинна основна точка H 2 визначаються аналогічним чином (див. Малюнок праворуч на малюнку\(\PageIndex{9}\)). Основні площини не повинні бути всередині об'єктива. Зокрема, для меніскових лінз це не так. З малюнка 2.18 видно, що головні площини є зображеннями один одного з одиничним збільшенням. Отже, якщо об'єкт розміщений у первинній головній площині (гіпотетично, якщо ця площина знаходиться всередині лінзи), його зображення знаходиться у вторинній головній площині. Зображення прямостояче і має одиничне збільшення.

Нагадаємо результат (\(\PageIndex{32}\)) для променевої матриці між площинами через передню і задню вершини V 1, V 2 товстої лінзи з показником заломлення n l і товщиною d:
\[M_{V_{1}V_{2}}=\begin{pmatrix} 1-\dfrac{d}{n_{l}}P_{2} & -P \\ \dfrac{d}{n_{l}} & 1-\dfrac{d}{n_{l}}P_{1} \end{pmatrix},thick\space lens, \nonumber \]
де
\[P_{1}=\dfrac{n_{l}-n_{m}}{R_{1}},P_{2}=\dfrac{n_{m}-n_{l}}{R_{2}}, \nonumber \]
а n m - показник заломлення навколишнього середовища, а
\[P=P_{1}+P_{2}-\dfrac{d}{n_{l}}P_{1}P_{2}. \nonumber \]
Якщо h 1 - z-координата першої головної точки H 1 по відношенню до системи координат з початковою вершиною V 1, то маємо відповідно (\(\PageIndex{27}\)) для матриці променя між первинною головною площиною і площиною через вершину V 1
\[M_{1}=\begin{pmatrix} 1 & 0 \\ \dfrac{h_{1}}{n_{m}} & 1\end{pmatrix}. \nonumber \]
Аналогічно, якщо h 2 - координата вторинної головної точки H 2 щодо системи координат з V 2 як початок, матриця променя між площиною через вершину V 2 і вторинною основною площиною дорівнює
\[M_{2}=\begin{pmatrix} 1 & 0 \\ \dfrac{h_{2}}{n_{m}} & 1\end{pmatrix}. \nonumber \]
Потім матриця променів між двома принциповими площинами
\[M_{H_{1}H_{2}}=M_{2}M_{V_{1}V_{2}}M_{1}. \nonumber \]
Координати h1 і h2 можна знайти, наклавши на отриману матрицю умову зображення (\(\PageIndex{41}\)): C = 0 і умову, що збільшення має бути одиницею: D = 1, що випливає з (\(\PageIndex{42}\)). Опускаємо деталі і наводимо тільки отримані вирази тут:
\[h_{1}=\dfrac{n_{m}}{n_{l}}\dfrac{P_{2}}{P}d, \nonumber \]
\[h_{2}=-\dfrac{n_{m}}{n_{l}}\dfrac{P_{1}}{P}d. \nonumber \]
Крім того, (\(\PageIndex{64}\)) стає
\[M_{H_{1}H_{2}}=\begin{pmatrix} 1 & -P \\ 0 & 1\end{pmatrix}. \nonumber \]
Ми бачимо, що променева матриця між основними площинами ідентична променевої матриці тонкої лінзи (\(\PageIndex{35}\)). Тому робиться висновок, що якщо координати в об'єктному просторі обрані відносно початку в первинній головній точці H 1, а координати в просторі зображення вибираються відносно початку у вторинній головній точці H 2, то вирази для першої та другої фокусні точки та координати точки зображення з точки зору точки об'єкта ідентичні координатам для тонкої лінзи. Приклад візуалізації товстою лінзою показаний на рис\(\PageIndex{11}\).

2.5.8 Зупинки
Такий елемент, як ободок лінзи або діафрагма, який визначає набір променів, які можуть сприяти зображенню, називається зупинкою діафрагми. Звичайна камера має змінну діафрагму.
Вхідний зіниця - це зображення зупинки діафрагми всіма елементами зліва від зупинки діафрагми. Якщо між об'єктом і зупинкою діафрагми немає лінз, зупинка діафрагми сама по собі є вхідним зіницею. Аналогічно вихідним зіницею є зображення зупинки діафрагми всіма елементами праворуч від нього. Вхідний зіниця визначає для даного предмета конус променів, що надходить в оптичну систему, в той час як конус променів, що йдуть і беруть участь у формуванні зображення, визначається вихідним зіницею (див. Рис.\(\PageIndex{12}\)). Зверніть увагу, що при побудові вхідного зіниці як зображення діафрагми зупиняються лінзами зліва від нього, поширюються справа наліво. Звідси зупинка апертури є реальним об'єктом в цій конструкції, тоді як вхідний зіниця може бути реальним або віртуальним зображенням. Промені, що використовуються при побудові вихідної зіниці як зображення зупинки діафрагми лінзами, наступними за зупинкою, поширюються зліва направо. Отже, також у цьому випадку зупинка діафрагми є реальним об'єктом, тоді як вихідна зіниця може бути реальним або віртуальним зображенням зупинки діафрагми.
Для будь-якої точки об'єкта головний промінь - це промінь у конусі, який проходить через центр вхідної зіниці, а отже, і через центри зупинки отвору та вихідної зіниці. Крайовий промінь - це промінь, який для предметної точки на оптичній осі проходить через обід вхідної зіниці (а значить, і через обідки зупинки отвору і вихідної зіниці).
Для фіксованого діаметра D вихідної зіниці та заданого x o, збільшення системи відповідно до (\(\PageIndex{50}\)) та (\(\PageIndex{48}\)), заданого M = −x i /f i = f i/x o. Звідси випливає, що при збільшенні ifi збільшення збільшується. Більше збільшення означає меншу щільність енергії, отже, більший час експозиції, тобто швидкість лінзи зменшується. Об'єктиви фотоапарата зазвичай задаються двома числами: фокусною відстанню f i і діаметром D вихідної зіниці. f-число - це відношення фокусної відстані до цього діаметру:
\[f-number=\dfrac{f}{D}. \nonumber \]
Наприклад, f-число = 2 означає f = 2D. Оскільки час експозиції пропорційно квадрату f-числа, об'єктив з f-числом 1.4 в два рази швидше, ніж лінза з f-номером 2.
