2.8: аберації
- Page ID
- 78778
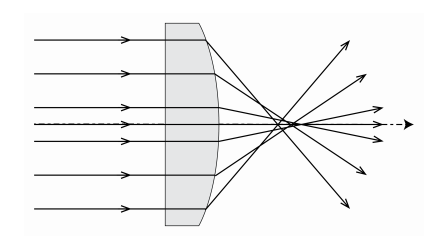
Для проектування передових оптичних систем гаусової геометричної оптики недостатньо. Замість непараксиальних променів, а серед них також немеридіональні промені, повинні простежуватися за допомогою програмного забезпечення, заснованого на Законі Снелла з синусом кутів падіння і заломлення. Часто багато тисяч променів простежуються, щоб оцінити якість зображення. Потім з'ясовується, що в цілому непараксіальні промені не перетинаються в ідеальній точці зображення Гаусса. Замість однієї плями виявляється точкова діаграма, яка більш-менш обмежена. Відхилення від ідеальної точки зображення кількісно визначається з точки зору аберацій. Розрізняють монохроматичні та хроматичні аберації. Останні викликані тим, що показник заломлення залежить від довжини хвилі. Нагадаємо, що в парааксіальній геометричній оптиці Закон Снелла (2.3.7) замінений на: n i θ i = n t θ t, тобто sin θ i і sin θ t замінюються на лінійні члени. Якщо замість цього один зберігає перші два члени серії Тейлора синуса, помилки на зображенні можуть бути кількісно визначені п'ятьма монохроматичними абераціями, так званими первинними абераціями або абераціями Зайделя. Найвідомішою є сферична аберація, яка викликана тим, що для сходяться сферичної лінзи промені, що утворюють великий кут з оптичною віссю, фокусуються ближче до лінзи, ніж параксіальні промені (див.\(\PageIndex{1}\) Рис. Спотворення - одна з п'яти первинних аберацій. Він викликає деформацію зображень через те, що збільшення залежить від відстані точки об'єкта до оптичної осі.
Для отримання високоякісної візуалізації аберації повинні бути зменшені шляхом додавання більшої кількості лінз та оптимізації викривлень поверхонь, товщини лінз та відстані між ними. Для систем високої якості іноді використовують лінзу з асферичною поверхнею. Системи з дуже малими абераціями надзвичайно дорогі, особливо якщо поле зору велике, як це відбувається в літографічних системах візуалізації, що використовуються у виробництві інтегральних схем.
2.7.1 Дифракційна оптика
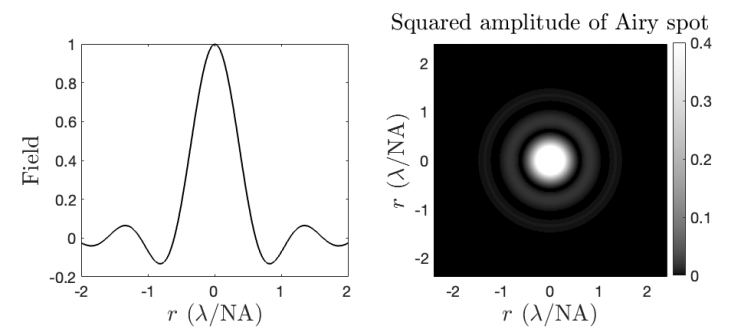
Аберації можна кількісно визначити, аналізуючи точкову діаграму або, альтернативно, враховуючи форму фактичного хвильового фронту в просторі зображення, який у гаусовій геометричній оптиці сходиться до точки зображення Гаусса. Аберації викликають відхилення хвильового фронту від досконалої сфери. Відповідно до загальноприйнятого критерію, сформульованого спочатку Релеєм, аберації починають значно погіршувати зображення, якщо аберації хвильового фронту спричиняють різницю довжини шляху більше чверті довжини хвилі. Коли аберації менше цього, система називається дифракцією обмеженою. Дуже комплексне лікування теорії аберацій можна знайти в книзі Braat et al. Навіть якщо хвиля, що передається вихідним зіницею, була б ідеально сферичною, хвильовий фронт складається лише з кругового перерізу сфери, оскільки поле обмежене діафрагмою. Діафрагма викликає дифракцію, тобто згинання та поширення світла. Коли один зображує точковий об'єкт на оптичній осі, дифракція викликає розподіл світла, який називається плямою Ейрі, як показано на малюнку\(\PageIndex{3}\). Пляма Airy має повну ширину на половину максимуму:
\[FWHM=0.6\dfrac{λ}{NA}, \nonumber \]
з NA = arcsin (a/si) - числова апертура (тобто 0<NA <1) з радіусом вихідної зіниці і si відстань зображення, як передбачено гаусовою геометричною оптикою. Дифракція залежить від довжини хвилі і, отже, вона не може бути описана геометричною оптикою, яка застосовується в межі довжини хвилі зникаючої. Ми будемо розглядати дифракцію діафрагмами в главі 6.