5.3: Загальне рішення для затухаючого гармонічного осцилятора
- Page ID
- 79780
А поки припустимо\(\omega_0 \ne \gamma\). У попередньому розділі ми знайшли два класи специфічних розв'язків зі складними частотами\(\omega_+\) і\(\omega_-\):\[z_+(t) = e^{-i\omega_+ t} \;\;\mathrm{and}\;\; z_-(t) = e^{-i\omega_- t}, \;\;\mathrm{where} \;\;\; \omega_\pm = -i\gamma \pm \sqrt{\omega_0^2 - \gamma^2}.\] Загальне рішення можна знайти шляхом побудови лінійної суперпозиції цих розв'язків:\[\begin{align} z(t) &= \psi_+ e^{-i\omega_+ t} + \psi_- e^{-i\omega_- t} \\ &= \psi_+ \, \exp\left[\left(-\gamma - i \sqrt{\omega_0^2 - \gamma^2}\right)t\right] \; +\; \psi_- \, \exp\left[\left(-\gamma +i\sqrt{\omega_0^2 - \gamma^2}\right)t\right]. \label{gensol}\end{align}\] Він містить два невизначені комплексні параметри, \(\psi_+\)і\(\psi_-\). Це незалежні параметри, оскільки вони є коефіцієнтами, що множать різні функції (функції різні, оскільки це\(\omega_0 \ne \gamma\) означає\(\omega_+ \ne \omega_-\)).
Для отримання загального розв'язку дійсного затухаючого гармонічного рівняння осцилятора необхідно взяти дійсну частину комплексного розв'язку. Результат можна додатково спростити в залежності від того,\(\omega_0^2 - \gamma^2\) позитивний чи негативний. Це призводить до недогашених рішень або надмірно затухаючих рішень, як обговорюється в наступних підрозділах.
Що робити, якщо\(\omega_0 = \gamma\)? У цьому випадку\(\omega_+ = \omega_-\), що означає, що\(\psi_+\) і\(\psi_-\) не є незалежними параметрами. Тому наведене вище рівняння для\(z(t)\) не є дійсним загальним рішенням! Ми обговоримо, як впоратися з цією справою Розділ 5.3.
Рух під затуханням
Для\(\omega_0 > \gamma\), давайте визначимо, для зручності,\[\Omega = \sqrt{\omega_0^2 - \gamma^2}.\] Тоді ми можемо спростити реальне рішення наступним чином:\[\begin{align} x(t) &= \mathrm{Re}\left[z(t)\right] \\ &= e^{-\gamma t} \; \mathrm{Re}\left[\psi_+ \, e^{-i \Omega t} \,+\, \psi_- \, e^{i\Omega t}\right] \\ &= e^{-\gamma t} \left[ A\cos\left(\Omega t\right) + B \sin\left(\Omega t\right)\right], \;\;\mathrm{where}\;\; A, B \in \mathbb{R} \label{underdamped-sol}\end{align}\] З трохи алгебри, ми можемо показати, що\[A = \mathrm{Re}\left[\psi_+ + \psi_-\right], \quad B = \mathrm{Im}\left[\psi_+ - \psi_-\right].\] це називається недогашене рішення. Коефіцієнти\(A\) і\(B\) діють як два незалежних дійсних параметра, тому це дійсне загальне рішення для реального затухаючого гармонічного рівняння осцилятора. Використовуючи тригонометричні формули, рішення можна рівнозначно записати як\[x(t) = C e^{-\gamma t} \cos\left[\Omega t + \Phi\right],\] з параметрами, так\(C = \sqrt{A^2 + B^2}\) і\(\Phi = - \tan^{-1}\left[B/A\right]\).
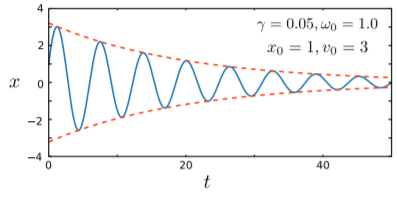
Як показано нижче, траєкторія - це коливання, амплітуда якого зменшується з часом. Зменшення амплітуди можна візуалізувати за допомогою плавного «конверта»\(\pm C e^{-\gamma t}\), заданого шляхом, який малюється рисками на малюнку. Усередині цієї оболонки траєкторія коливається з частотою\(\Omega = \sqrt{\omega_0^2 - \gamma^2}\), яка трохи менше власної частоти коливань\(\omega_0\).
Надмірно затухаючий рух
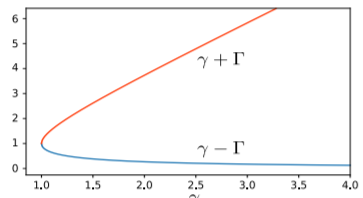
Бо\(\omega_0 < \gamma\), квадратний корінь термін є уявним. Це зручно визначити\[\Gamma = \sqrt{\gamma^2 - \omega_0^2} \quad \Rightarrow \quad \sqrt{\omega_0^2 - \gamma^2} = i \Gamma.\] Тоді реальне рішення спрощує по-іншому:\[\begin{align} x(t) = \mathrm{Re}\left[z(t)\right] &= \mathrm{Re}\left[\psi_+ e^{\left(-\gamma + \Gamma\right)t} + \psi_- e^{\left(-\gamma - \Gamma\right)t} \right] \\ &= C_+ e^{-(\gamma - \Gamma) t} + C_- e^{-(\gamma + \Gamma) t}, \label{overdamped-sol}\end{align}\] де\[C_\pm = \mathrm{Re}[\psi_\pm].\] це називається надмірно затухаючим рішенням. Він складається з двох термінів, обидва експоненціально розкладаються в часі, з\((\gamma-\Gamma)\) і\((\gamma + \Gamma)\) служать швидкістю розпаду. Зверніть увагу, що обидві швидкості розпаду є позитивними дійсними числами, тому що\(\Gamma < \gamma\) з визначення\(\Gamma\). Крім того, зверніть увагу, що\((\gamma - \Gamma)\) зменшується з\(\gamma\), тоді як\((\gamma + \Gamma)\) збільшується з\(\gamma\), як показано нижче:
На графіку нижче показана траєкторія надмірно затухаючого осцилятора:
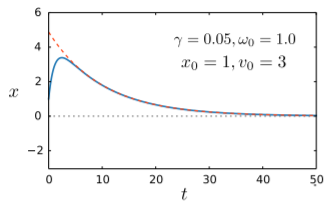
Червоні риски показують граничну криву, визначену швидкістю розпаду\((\gamma - \Gamma)\). Інша швидкість розпаду відповідає швидшому розкладанню експоненції, тому в довгий час другий термін в еквалайзері.\((\gamma + \Gamma)\) \(\eqref{overdamped-sol}\)стає незначним порівняно з першим терміном. Тоді рішення наближається до межі\[x(t) \approx C_+ e^{-(\gamma - \Gamma) t} \qquad (\mathrm{for}~\mathrm{large}~t). \label{overdamped-long-t}\] Цікаво, оскільки\((\gamma-\Gamma)\) є спадною функцією\(\gamma\), чим сильніше демпфування, тим повільніше швидкість розпаду в довгий час. Це протилежне тому, що відбувається в недогашеному режимі!
Чому це відбувається? У надмірно затухаючому режимі рух осцилятора переважає сила демпфування, а не сила пружини; оскільки генератор намагається повернутися в положення рівноваги\(x = 0\), демпфування діє проти цього руху. Отже, чим сильніше демпфування, тим повільніше відбувається розпад до рівноваги. Це різко контрастує з Розділом 5.3, де сила пружини домінує над силою демпфування. У цьому випадку сильніше демпфування прискорює розпад до рівноваги, змушуючи кінетичну енергію коливання швидше розсіюватися.
Критичне демпфування
Критичне демпфування відбувається при\(\omega_0 = \gamma\). За цієї особливої умови, Eq. \(\eqref{gensol}\)зводиться до\[z(t) = \left(\psi_+ + \psi_-\right) e^{-\gamma t}.\] Це має тільки один незалежний комплексний параметр, тобто параметр\((\psi_+ + \psi_-)\). Тому це не може бути загальним рішенням для комплексного затухаючого гармонічного рівняння осцилятора, яке все ще є ODE другого порядку.
Ми не будемо вдаватися тут в подробиці щодо процедури пошуку загального рішення для критично затухаючого осцилятора, залишивши його як Розділ 5.5 для зацікавленого читача. В основному, процедура Тейлора полягає в тому, щоб розширити рішення по обидва боки критичної точки, а потім показати, що існує рішення форми,\[z(t) = \left(A + B t\right)\, e^{-\gamma t}, \label{critical-sol}\] яка містить бажані два незалежних параметра.
Критично затухаючий розчин містить експоненціальну константу розпаду\(\gamma\), яка є такою ж, як і константа розпаду для функції огинаючої в недозатухаючому режимі [Eq. \(\eqref{underdamped-sol}\)], і менше, ніж довготривалі константи розпаду в надмірно затухаючому режимі [Eq. \(\eqref{overdamped-long-t}\)]. Отже, ми можемо розглядати критично затухаюче рішення як найбільш швидко розпадається неколивальне рішення.
Ця особливість критичного демпфування використовується в багатьох інженерних контекстах, найбільш звичним є автоматичні доводчики дверей. Якщо демпфування занадто слабке або сила пружини занадто сильна (недостатньо демпфірована), двері закриються, тоді як якщо демпфування занадто сильне або сила пружини занадто слабка (недостатнє демпфування), двері займе надмірно багато часу, щоб закритися. Отже, дверні доводчики повинні бути налаштовані на «солодке місце», відповідне критичній точці демпфування.