13.E: Оптика (вправи)

1. Намалюйте променеву діаграму, яка показує, чому маленьке джерело світла (скажімо, свічка) створює більш різкі тіні, ніж великий (наприклад, довга люмінесцентна лампа).

2. Приймач Глобальної системи позиціонування (GPS) - це пристрій, який дозволяє з'ясувати, де ви знаходитесь, отримуючи приурочені радіосигнали від супутників. Він працює шляхом вимірювання часу в дорозі для сигналів, що пов'язано з відстанню між вами і супутником. Знайшовши діапазони до декількох різних супутників таким чином, він може визначити ваше місцезнаходження в трьох вимірах в межах декількох метрів. Наскільки точним має бути вимірювання затримки часу, щоб визначити вашу позицію з цією точністю?

3. Оцініть частоту електромагнітної хвилі, довжина хвилі якої за розмірами аналогічна атому (близько нм). Повертаючись до малюнка o на стор. 703, в якій частині електромагнітного спектра лягла б така хвиля (інфрачервоні, гамма-промені,...)?

4. Бомбардувальник Stealth розроблений з плоскими, гладкими поверхнями. Чому це ускладнює виявлення за допомогою радара?

a/ Задача 5.

5. Вихідці з планети Wumpus грають в більярд, використовуючи світлові промені на одинадцятисторонньому столі з дзеркалами для бамперів, показаних на малюнку на наступній сторінці. Проведіть цей постріл точно за допомогою лінійки, щоб виявити приховане повідомлення. Щоб отримати достатню точність, вам потрібно буде ксероскопіювати сторінку (або завантажити книгу і роздрукувати сторінку) і побудувати кожне відображення за допомогою транспортира.

b/Задача 6.

6. На малюнку на наступній сторінці зображено вигнуте (параболічне) дзеркало з трьома паралельними променями світла, що йдуть до нього. Один промінь наближається вздовж центральної лінії дзеркала. (а) Точно простежте малюнок і продовжуйте світлові промені, поки вони не пройдуть друге відображення. Щоб отримати досить хорошу точність, вам потрібно буде ксероскопіювати сторінку (або завантажити книгу і роздрукувати сторінку) і малювати в нормі в кожному місці, де відбивається промінь. Що ви помічаєте? (б) Складіть приклад практичного використання цього пристрою. (c) Як ви могли використовувати це дзеркало з невеликою лампочкою для створення паралельного пучка світлових променів, що йдуть вправо?

7. (Перевірка відповіді доступна на lightandmatter.com) Людина йде зі швидкістю 1,0 м/с прямо до плоского дзеркала. З якою швидкістю зменшується його відрив від образу?

8. Якщо дзеркало на стіні достатньо велике, щоб ви могли бачити себе від голови до талії, чи можете ви побачити все своє тіло, резервне копіювання? Перевірте це експериментальним шляхом і придумайте пояснення для своїх спостережень, включаючи променеву діаграму.

Зверніть увагу, що коли ви робите експеримент, легко заплутати себе, якщо дзеркало навіть трохи відривається від вертикалі. Один із способів перевірити себе - штучно опустити верхню частину дзеркала, поклавши шматок стрічки або записку після неї, де вона блокує ваш погляд на верхівку голови. Потім ви можете перевірити, чи можете ви бачити більше себе як вище, так і нижче, резервне копіювання.

9. У розділі 12.2 ми зробили лише приклади дзеркал з видовбленими формами (звані увігнутими дзеркалами). Тепер намалюйте променеву діаграму для вигнутого дзеркала, яке має випирає назовні форму (називається опуклим дзеркалом). (а) Як відстань зображення від дзеркала порівнюється з фактичною віддаленістю об'єкта від дзеркала? З цього порівняння визначте, чи збільшення більше або менше одиниці. (b) Зображення реальне чи віртуальне? Чи може це дзеркало коли-небудь зробити інший тип зображення?

10. Як обговорюється в питанні 9, існує два типи криволінійних дзеркал, увігнуті і опуклі. Складіть список всіх можливих комбінацій типів зображень (віртуальних або реальних) з типами дзеркал (увігнутих і опуклих). (Не всі з чотирьох комбінацій фізично можливі.) Тепер для кожного використовуйте променеві діаграми, щоб визначити, чи призводить збільшення відстані об'єкта від дзеркала до збільшення або зменшення відстані зображення від дзеркала.

Намалюйте ВЕЛИКІ діаграми променів! Кожна схема повинна зайняти близько половини сторінки паперу.

Кілька порад: Щоб намалювати променеву діаграму, вам знадобляться два промені. Для одного з них виберіть промінь, який йде прямо вздовж осі дзеркала, оскільки його відображення легко намалювати. Після того, як ви намалюєте два промені і знайдете зображення для початкового положення об'єкта, виберіть нову позицію об'єкта, що призводить до того ж типу зображення, і розпочніть нову діаграму променів іншим кольором пера, прямо над першим. Для двох нових променів виберіть ті, які просто потрапляють у дзеркало в тих же двох місцях; це значно полегшує отримання результату правильно, не залежно від надзвичайної точності у вашій здатності малювати відбиті промені.

11. Якщо користувач астрономічного телескопа рухає голову ближче або далі від зображення, на яке вона дивиться, чи змінюється збільшення? Чи змінюється кутове збільшення? Поясніть. (Для простоти припустимо, що жоден окуляр не використовується.)

12. На малюнку г/2 в на сторінці 752 тільки зображення мого чола розташовувалося шляхом малювання променів. Або ксерокопіювати малюнок, або завантажити книгу і роздрукувати відповідну сторінку. На цій копії фігури зробіть новий набір променів, що йдуть від підборіддя, і знайдіть його зображення. Щоб легше було точно судити про кути, намалюйте промені від підборіддя, які трапляються потрапляти в дзеркало в тих же точках, де були показані два промені від чола, що потрапляють в нього. Порівнюючи місця зображення підборіддя та зображення чола, переконайтеся, що зображення насправді перевернуте, як показано на вихідному малюнку.

c/Задача 13.

13. На малюнку зображені чотири точки, де промені перетинаються. З них, які точки зображення? Поясніть.

14. Ось гра, яку люблять грати мої діти. Я сиджу поруч із сонячним вікном, і сонце відбивається від скла на моєму годиннику, роблячи диск світла на стіні або підлозі, який вони роблять вигляд, що переслідують, коли я його переміщаю. Чи є пляма диском, тому що це форма сонця, або тому, що це форма мого годинника? Іншими словами, квадратний годинник зробить квадратну пляму, або ми просто маємо кругове зображення кругового сонця, яке буде круговим, незважаючи ні на що?

15. Застосовуємо рівняння\(M=d_i/d_o\) до випадку плоского дзеркала.

16. (Рішення у pdf-версії книги) Використовуйте метод, описаний у тексті, щоб вивести рівняння, що стосується відстані об'єкта до відстані зображення, для випадку віртуального зображення, отриманого збіжним дзеркалом.

17. Знайти фокусну відстань дзеркала в задачі 6. (Перевірка відповіді доступна на сайті lightandmatter.com)

d/Задача 18.

18. Перерахуйте фокусні відстані дзеркал на малюнку, від найкоротшого до найдовшого. Поясніть.

19. (Рішення в pdf-версії книги) (а) Для створення зображення використовується сходяться дзеркало з фокусною відстанню 20 см, використовуючи предмет на відстані 10 см. Зображення реальне, або воно віртуальне? (b) Як приблизно\(f=20\) см і\(d_o=30\) см? (c) Що робити, якщо це було розходяться дзеркало з\(f=20\) см і\(d_o=10\) см? (г) Розходяться дзеркало з\(f=20\) см і\(d_o=30\) см?

20. (а) Складіть числовий приклад віртуального зображення, утвореного збіжним дзеркалом з певною фокусною відстанню, і визначте збільшення. (Вам знадобиться результат завдання 16.) Переконайтеся, що ви\(d_o\) вибираєте значення і\(f\) що б фактично створити віртуальний образ, а не реальний. Тепер трохи змініть розташування об'єкта і заново визначте збільшення, показавши, що воно змінюється. У моєму місцевому універмазі відділ косметики продає ручні дзеркала, рекламовані як збільшення в 5 разів. Як би ви це інтерпретували?

(b) Припустимо, що для астрономічних спостережень використовується ньютонівський телескоп. Припустимо для простоти, що жоден окуляр не використовується, і припустимо значення фокусної відстані дзеркала, яке було б розумним для аматорського інструменту, який повинен поміститися в шафі. Чи відрізняється кутове збільшення для об'єктів на різній відстані? Наприклад, можна було б розглянути дві планети, одна з яких вдвічі більша за іншу.

21. (а) Знайдіть випадок, коли збільшення вигнутого дзеркала нескінченне. Чи є кутове збільшення нескінченним від будь-якого реалістичного положення перегляду? (б) Поясніть, чому довільно велике збільшення не може бути досягнуто, маючи досить мале значення\(d_o\).

22. Увігнута поверхня, яка відображає звукові хвилі, може діяти так само, як сходяться дзеркало. Припустимо, що, стоячи біля такої поверхні, ви здатні знайти точку, де можна розташувати голову так, щоб власний шепіт був зосереджений назад на голові, щоб вони звучали голосно для вас. Враховуючи вашу відстань до поверхні, яка фокусна відстань поверхні?

e/Задача 23.

23. На малюнку зображено пристрій для побудови реалістичної оптичної ілюзії. Два дзеркала однакової фокусної відстані ставляться один до одного посрібленими поверхнями, зверненими всередину. Невеликий предмет, поміщений в нижній частині порожнини, матиме своє зображення, яке проектується в повітрі вище. Спосіб роботи полягає в тому, що верхнє дзеркало виробляє віртуальне зображення, а нижнє дзеркало потім створює реальний образ віртуального зображення. (а) Показати, що якщо зображення потрібно розташувати, як показано, в гирлі порожнини, то фокусна відстань дзеркал пов'язана з розмірністю\(h\) за допомогою рівняння

\[\begin{equation*} \frac{1}{f} = \frac{1}{h}+\frac{1}{h+\left(\frac{1}{h}-\frac{1}{f}\right)^{-1}} . \end{equation*}\]

(b) Повторити рівняння через одну змінну і показати\(x=h/f\), що існує два рішення для\(x\). Яке рішення фізично відповідає припущенням розрахунку?

24. (a) Для створення віртуального образу використовується дзеркало, що сходиться. Який діапазон можливих збільшень? (б) Зробіть те ж саме для інших типів зображень, які можуть бути сформовані вигнутими дзеркалами (як сходяться, так і розходяться).

25. Розходяться дзеркало фокусної відстані\(f\) фіксується, і обличчям вниз. З поверхні дзеркала опускається предмет, і відпадає від нього з прискоренням\(g\). Мета завдання - знайти максимальну швидкість зображення.
(а) Опишіть рух зображення усно та поясніть, чому ми повинні очікувати максимальної швидкості.
(б) Використовуйте аргументи, засновані на одиницях, для визначення форми розв'язку, аж до невідомої безодиничної мультиплікативної константи.
(c) Завершіть рішення, визначивши безодиничну константу.

26. Алмаз має показник заломлення 2,42, і частина причини, чому діаманти блищать, полягає в тому, що це спонукає світловий промінь зазнати багатьох загальних внутрішніх відображень, перш ніж він з'явиться. (а) Обчисліть критичний кут, під яким відбувається повне внутрішнє відображення в алмазу. (Перевірка відповіді доступна на сайті lightandmatter.com) (b) Поясніть інтерпретацію вашого результату: це вимірюється від норми або з поверхні? Це мінімум, або максимум? Як би різнився критичний кут для такої речовини, як скло або пластик, з меншим показником заломлення?

27. Припустимо, що сходяться лінза побудована з типу пластика, показник заломлення якого менше, ніж у води. Як буде відрізнятися поведінка об'єктива, якщо він розміщений під водою?

28. Існує два основних типи телескопів, заломлюючі (за допомогою лінзи) і відображають (з використанням дзеркала, як на малюнку i на стор. 754). (Деякі телескопи використовують суміш двох типів елементів: світло спочатку стикається з великим вигнутим дзеркалом, а потім проходить через окуляр, який є лінзою. Щоб все було просто, припустимо, що жоден окуляр не використовується.) Які наслідки матиме колірна залежність фокусної відстані для відносних переваг двох типів телескопів? Опишіть випадок, коли утворюється зображення білої зірки. Можливо, вам буде корисно намалювати діаграму променів.

29. Виходячи із закону Снелла, поясніть, чому промені світла, що проходять через краї сходяться лінзи, зігнуті більше, ніж промені, що проходять через частини ближче до центру. Може здатися, що це повинно бути навпаки, оскільки промені на краю проходять через менше скла - чи не повинні вони постраждати менше? У вашій відповіді:

• Включіть променеву діаграму, що показує величезний, повносторінковий, крупним планом вид відповідної частини об'єктива.
• Використовуйте той факт, що передня і задня поверхні не завжди паралельні; лінза, в якій передня і задня поверхні завжди паралельні, взагалі не фокусує світло, тому, якщо ваше пояснення не використовує цей факт, ваш аргумент повинен бути неправильним.
• Переконайтеся, що ваш аргумент все ще працює, навіть якщо промені не йдуть паралельно осі.

30. Коли ви робите знімки за допомогою камери, відстань між об'єктивом і плівкою потрібно регулювати, залежно від відстані, на якій ви хочете сфокусуватися. Робиться це за допомогою переміщення лінзи. Якщо ви хочете змінити фокус, щоб ви могли сфотографувати щось далі, яким чином вам доведеться перемістити об'єктив? Поясніть, використовуючи променеві діаграми. [На основі проблеми Еріка Мазура.]

31. Під час плавання під водою, чому ваше бачення стає набагато чіткішим, одягаючи окуляри з плоскими шматочками скла, які затримують повітря за ними? [Підказка: Ви можете спростити свої міркування, розглянувши особливий випадок, коли ви дивитеся на об'єкт далеко і вздовж оптичної осі ока.]

32. (Перевірка відповіді доступна на сайті lightandmatter.com) Об'єкт має більше однієї фокусної відстані від об'єктива, що сходиться. (а) Намалюйте діаграму променів. (b) Використовуючи міркування, подібні до того, що розроблено в розділі 12.3, визначте позитивні та негативні знаки в рівнянні\(1/f=\pm1/d_i\pm1/d_o\). (c) Зображення троянди в розділі 4.2 були зроблені за допомогою лінзи з фокусною відстанню 23 см. Якщо лінза розміщена в 80 см від троянди, знайдіть зображення.

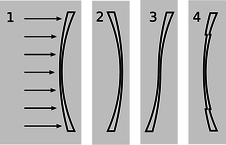
f/Задача 33.

33. На малюнку зображені чотири лінзи. Лінза 1 має дві сферичні поверхні. Об'єктив 2 такий же, як об'єктив 1, але повернутий навколо. Лінза 3 виготовляється шляхом прорізання лінзи 1 і повороту дна навколо. Лінза 4 виготовляється шляхом вирізання центрального кола з лінзи 1 і заглиблення його.

(а) Паралельний промінь світла потрапляє в лінзу 1 зліва, паралельно її осі. Міркування, засновані на законі Снелла, чи буде промінь, що виходить з лінзи, зігнутий всередину, або він залишиться паралельним осі? Поясніть свої міркування. В рамках вашої відповіді зробіть величезний малюнок однієї невеликої частини об'єктива, і застосуйте закон Снелла на обох інтерфейсах. Нагадаємо, що промені більше згинаються, якщо вони потрапляють на межі розділу під більшим кутом по відношенню до нормального.

(б) Що буде з лінзами 2, 3 і 4? Поясніть. Креслення робити не потрібно.

g/Задача 34.

34. На малюнку показана анатомія людського ока, в два рази в натуральну величину. Знайти радіус кривизни зовнішньої поверхні рогівки шляхом вимірювань на малюнку, а потім вивести фокусну відстань інтерфейсу повітря-рогівка, де відбувається майже все фокусування світла. Вам потрібно буде використовувати фізичні міркування, щоб змінити рівняння об'єктива для випадку, коли є лише одна заломлююча поверхня. Припустимо, що показник заломлення рогівки по суті є показником води.

35. (Перевірка відповіді доступна на сайті lightandmatter.com) Об'єкт має меншу фокусну відстань від об'єктива, що сходиться. (а) Намалюйте діаграму променів. (b) Використовуючи міркування, подібні до того, що розроблено в розділі 12.3, визначте позитивні та негативні знаки в рівнянні\(1/f=\pm1/d_i\pm1/d_o\). (c) Зображення троянди в розділі 4.2 були зроблені за допомогою лінзи з фокусною відстанню 23 см. Якщо лінза розміщена в 10 см від троянди, знайдіть зображення.

36. (Перевірка відповіді доступна на сайті lightandmatter.com) Короткозорі люди носять окуляри, лінзи яких розходяться. (а) Намалюйте діаграму променів. Для простоти зробіть вигляд, що за окулярами немає ока. (b) Використовуючи міркування, подібні до того, що розроблено в розділі 12.3, визначте позитивні та негативні знаки в рівнянні\(1/f=\pm1/d_i\pm1/d_o\). (c) Якщо фокусна відстань об'єктива становить 50,0 см, а людина дивиться на об'єкт на відстані 80,0 см, знайдіть зображення.

37. (a) Світло відбивається дифузно від об'єкта 1.000 м під водою. Світло, що виходить на поверхню, заломлюється на межі розділу вода-повітря. Якщо заломлені промені все здаються надходять з однієї точки, то з'явиться віртуальне зображення об'єкта у воді, над фактичним положенням об'єкта, яке буде видно спостерігачеві над водою. Розглянемо три променя, А, В і С, кути яких у воді по відношенню до нормальних є\(\theta_i=0.000°\),\(1.000°\) і\(20.000°\) відповідно. Знайдіть глибину точки, в якій заломлені частини A і B, здається, перетиналися, і зробіть те ж саме для A і C. Покажіть, що перетину знаходяться на майже однаковій глибині, але не зовсім. [Перевірка: Різниця в глибині повинна становити близько 4 см.]

(b) Оскільки всі заломлені промені, здається, не зовсім прийшли з однієї точки, це технічно не віртуальне зображення. У практичному плані, який вплив це матиме на те, що ви бачите?

(c) У випадку, коли всі кути малі, використовуйте алгебру та триг, щоб показати, що заломлені промені виходять з тієї ж точки, і знайдіть рівняння для глибини віртуального зображення. Не ставте ніяких числових значень для кутів або індексів заломлення — просто зберігайте їх як символи. Вам знадобиться наближення\(\sin\theta\approx \tan\theta\approx \theta\), яке справедливо для малих кутів, виміряних в радіанах.

38. Доведіть, що принцип найменшого часу призводить до закону Снелла.

h/Задача 39.

39. (Рішення в pdf-версії книги) Два стандартних фокусних відстані для об'єктивів камери - 50 мм (стандарт) і 28 мм (ширококутний). Щоб побачити, як фокусні відстані співвідносяться з кутовим розміром поля зору, корисно візуалізувати речі, як показано на малюнку. Замість того, щоб показувати багато променів, що надходять з однієї точки на одному об'єкті, як ми зазвичай робимо, на малюнку показано два промені від двох різних об'єктів. Хоча лінза буде перехоплювати нескінченно багато променів від кожної з цих точок, ми показали лише ті, які проходять через центр лінзи, так що вони не зазнають кутового відхилення. (Будь-яке кутове відхилення на передній поверхні лінзи скасовується протилежним відхиленням ззаду, так як передня і задня поверхні паралельні по центру лінзи.) Особливість цих двох променів полягає в тому, що вони спрямовані на краї одного кадру плівки шириною 35 мм; тобто показують межі поля зору. Протягом усієї цієї проблеми ми припускаємо,\(d_o\) що набагато більше, ніж\(d_i\). (a) Обчислити кутову ширину поля зору камери при використанні цих двох об'єктивів. (b) Використовуйте малокутові наближення, щоб знайти спрощене рівняння для кутової ширини поля зору\(\theta \), з точки зору фокусної відстані та ширини плівки,\(w\).\(f\) Ваше рівняння не повинно мати жодних тригових функцій у ньому. Порівняйте результати цього наближення з вашими відповідями з частини а. (c) Припустимо, що ми тримаємо постійну діафрагму (кількість площі поверхні лінзи, яка використовується для збору світла). При переході з 50-мм лінзи на 28-мм лінзу скільки разів довше або коротше повинна бути експозиція, щоб зробити правильно розроблену картинку, тобто таку, яка не знаходиться під- або переекспонованим? [На основі проблеми Арнольда Аронса.]

40. Короткозорка людина - це той, чиї очі фокусують світло занадто сильно, і тому не в змозі розслабити лінзу всередині ока достатньо, щоб сформувати зображення на її сітківці об'єкта, який знаходиться занадто далеко.

(а) Намалюйте променеву діаграму, яка показує, що відбувається, коли людина намагається з невиправленим зором зосередитися на нескінченності.

(б) Який тип лінз мають її окуляри? Поясніть.

(c) Намалюйте променеву діаграму, яка показує, що відбувається, коли вона носить окуляри. Знайдіть як зображення, утворене окулярами, так і остаточне зображення.

(d) Припустимо, що вона іноді використовує контактні лінзи замість своїх окулярів. Чи повинна фокусна відстань її контактів бути меншою, рівною або більшою, ніж у її окулярів? Поясніть.

41. Очі Фреда здатні зосередитися на речах близько 5,0 см. Фред тримає збільшувальне скло з фокусною відстанню 3,0 см на висоті 2, 0 см над плоским черв'яком. (a) Знайдіть зображення та знайдіть збільшення. (б) Без збільшувального скла, з якої відстані Фред хотів би переглянути плоского черв'яка, щоб якомога краще побачити його деталі? З лупою? (c) Обчислити кутове збільшення.

i/Задача 42.

42. На панелі 1 малюнка зображена оптика всередині пари біноклів. Вони, по суті, є парою телескопів, по одному на кожне око. Але щоб зробити їх більш компактними і дозволити окулярам бути на правильній відстані один від одного для людського обличчя, вони включають набір з восьми призм, які складають світловий шлях. Крім того, призми роблять зображення вертикальним. На панелі 2 зображена одна з цих призм, відома як призма Порро. Світло потрапляє по нормалі, зазнає два загальних внутрішніх відбиття під кутами 45 градусів по відношенню до задніх поверхонь і виходить уздовж нормальної. Зображення літери R було перевернуто по горизонталі. На панелі 3 зображена пара цих призм, склеєних між собою. Зображення буде перевертатися як по горизонталі, так і по вертикалі, що робить його орієнтованим правильним чином для користувача бінокля.

(а) Знайти мінімально можливий показник заломлення для скла, що використовується в призмах.
(б) Для матеріалу цього мінімального показника заломлення знайдіть частку вхідного світла, яка буде втрачена для відображення в чотирьох призмах Порро на кожній стороні пари біноклів. (Див. Розділ 6.2.) У справжніх, якісних біноклі оптичні поверхні призм мають антивідблиску покриття, але проведіть свій розрахунок для того випадку, коли такого покриття немає.
(c) Обговорити причини, чому дизайнер бінокль може або не може хотіти використовувати матеріал з точно індексом заломлення знайдених в частині а.

43. Було б дратувати, якби ваші окуляри створювали збільшене або зменшене зображення. Доведіть, що коли око знаходиться дуже близько до лінзи, а лінза виробляє віртуальне зображення, кутове збільшення завжди приблизно дорівнює 1 (незалежно від того, розходяться лінзи або сходяться).

44. На малюнку зображений дифракційний малюнок, зроблений подвійною щілиною, разом із зображенням метрової палиці, щоб показати масштаб. Намалюйте малюнок дифракції з малюнка на папері. Тепер розглянемо чотири змінні в рівнянні\(\lambda /d=\sin \theta /m\). Які з них однакові для всіх п'яти бахром, а які різні для кожної бахроми? Яку змінну ви, природно, використовували б для того, щоб позначити, яка бахрома яка? Позначте бахрому на вашому ескізі, використовуючи значення цієї змінної.

45. Зіставте решітки A-C з дифракційними малюнками 1-3, які вони виробляють. Поясніть.

46. На малюнку нижче показані дві дифракційні моделі. Верхній був зроблений жовтим світлом, а нижній - червоним. Чи могли прорізи, які використовуються для виготовлення двох візерунків, були однаковими?

j/Задачі 44 і 47.

47. На малюнку на стор. 805 зображений дифракційний малюнок, зроблений подвійною щілиною, разом із зображенням метрової палиці, щоб показати масштаб. Прорізи знаходилися на відстані 146 см від екрану, на якому проектувалася дифракційна картина. Відстань між прорізами становила 0,050 мм. Якою була довжина хвилі світла? (Перевірка відповіді доступна на сайті lightandmatter.com)

48. Чому блакитне або фіолетове світло буде найкращим для мікроскопії?

49. На малюнку нижче показані дві дифракційні моделі, обидва зроблені з однаковою довжиною хвилі червоного світла. (а) Який тип прорізів зробив візерунки? Це одинарна щілина, подвійні щілини або щось інше? Поясніть. (b) Порівняйте розміри щілин, які використовуються для виготовлення верхнього та нижнього візерунка. Дайте числове відношення і вкажіть, в який бік відношення, тобто який візерунок щілини був більшим. Поясніть.

50. Коли біле світло проходить через дифракційну решітку, що є найменшим значенням,\(m\) для якого видимий спектр порядку\(m\) перекриває наступний, порядку\(m+1?\) (видимий спектр проходить від приблизно 400 нм до приблизно 700 нм.)

k/Задача 51. Це зображення зоряного скупчення Плеяд показує ореоли навколо зірок завдяки хвильовій природі світла.

51. Для зображень зірок, таких як зображення на малюнку у, оцініть кутову ширину дифракційної плями через дифракцію в гирлі телескопа. Припустимо телескоп діаметром 10 метрів (найбільший в даний час існуючий) і світло з довжиною хвилі в середині видимого діапазону. Порівняйте з фактичним кутовим розміром зірки діаметром\(10^9\)\(10^{17}\) m, що видно з відстані м.

52. На малюнку нижче показані три дифракційні візерунки. Всі були зроблені в однакових умовах, за винятком того, що для кожної використовувався різний набір подвійних прорізів. Прорізи, які використовувалися для виготовлення верхнього візерунка, мали поділ від центру до центру\(d=0.50\) мм, а кожна щілина була шириною в\(w=0.04\) мм. (а) Визначте\(d\) і\(w\) для прорізів, використовуваних для виготовлення візерунка посередині. (b) Зробіть те ж саме для прорізів, використовуваних для виготовлення нижнього візерунка.

53. (Перевірка відповіді доступна на сайті lightandmatter.com) Промінь лазера проходить через дифракційну решітку, вивітрюється, і висвітлює стіну, яка перпендикулярна вихідному пучку, що лежить на відстані 2,0 м від решітки. Промінь виробляється гелій-неоновим лазером, і має довжину хвилі 694,3 нм. Решітка має 2000 ліній на сантиметр. (а) Яка відстань на стіні між центральним максимумом і максимумами відразу праворуч і ліворуч? (b) Наскільки змінюється ваша відповідь, коли ви використовуєте малокутові наближення\(\theta\approx\sin\theta\approx\tan\theta\)?

54. Ультразвук, тобто звукові хвилі з занадто високими частотами, щоб бути чутними, можуть бути використані для візуалізації плодів в утробі матері або для розщеплення каменів в нирках, щоб їх можна було усунути організмом. Розглянемо останнє застосування. Лінзи можуть бути побудовані для фокусування звукових хвиль, але оскільки довжина хвилі звуку не така мала порівняно з діаметром лінзи, звук не буде зосереджений точно в геометричній фокусній точці. Замість цього буде створено дифракційний візерунок з інтенсивним центральним плямою, оточеною слабкими кільцями. Близько 85% потужності зосереджено в межах центральної плями. Кут першого мінімуму (оточує центральну пляму)\(b\) задається тим\(\sin \theta =\lambda/b\), де - діаметр лінзи. Це схоже на відповідне рівняння для однієї щілини, але з коефіцієнтом 1,22 спереду, який виникає з круглої форми отвору. Нехай відстань від кришталика до ниркового каменю пацієнта складе\(L=20\) см. Ви захочете\(f>20\) кГц, щоб звук був нечутний. Знайдіть значення\(b\) і\(f\) що призведе до корисної конструкції, де центральна пляма досить мала, щоб лежати в нирковому камені діаметром 1 см.

55. За яких обставин можна отримати математично невизначений результат шляхом розв'язання двощілинного дифракційного рівняння\(\theta \)? Дайте фізичну інтерпретацію того, що насправді буде спостерігатися.

56. Коли ультразвук використовується для медичної візуалізації, частота може досягати 5-20 МГц. Ще одне медичне застосування ультразвуку - для терапевтичного нагрівання тканин всередині тіла; тут частота зазвичай становить 1-3 МГц. Які основні фізичні причини ви могли б запропонувати для використання більш високих частот для візуалізації?

л/Задача 57.

57. Припустимо, у нас багатокутне приміщення, стіни якого дзеркала, а в кімнаті є точкове джерело світла. У більшості таких прикладів кожна точка в кімнаті закінчується освітленням джерелом світла після деякої кінцевої кількості відображень. Складне математичне питання, вперше поставлене в середині минулого століття, полягає в тому, чи можна коли-небудь мати приклад, в якому не освітлюється вся кімната. (Вважається, що промені поглинаються, якщо вони вражають точно по вершині багатокутника, або якщо вони проходять точно через площину дзеркала.)

Проблема остаточно вирішила в 1995 році Г.В.Токарський, який знайшов приклад кімнати, яка не була освітлена з певної точки. На малюнку 57 показаний дещо простіший приклад, знайдений через два роки Д.Кастро. Якщо джерело світла розміщено в будь-якому з місць, показаних крапками, інша точка залишається неосвітленою, хоча кожна інша точка освітлена. Непросто суворо довести, що рішення Кастро має цю властивість. Однак правдоподібність рішення можна продемонструвати наступним чином.

Припустимо, джерело світла розміщено в правій точці. Знайдіть всі зображення, утворені одиночними відображеннями. Зверніть увагу, що вони утворюють звичайний візерунок. Переконайте себе, що жоден з цих зображень не висвітлює ліву крапку. Через регулярний візерунок стає правдоподібним, що навіть якщо ми формуємо зображення зображень, зображення зображень тощо, жодна з них ніколи не висвітлює іншу точку.

Існують і різні інші версії проблеми, деякі з яких залишаються невирішеними. Книга Клі і Вагона дає гарне вступ до теми, хоча вона передує творчості Токарського і Кастро.

Посилання:
Г.В.Токарський, «Полігональні кімнати, що не висвітлюються з кожної точки». Амер. Математика. Щомісячно 102, 867-879, 1995.
Д. Кастро, «Виправлення». Квантум 7, 42, січень 1997 року.
Клі та С.Вагон, Старі та нові нерозв'язані задачі в геометрії площини та теорії чисел. Математична асоціація Америки, 1991.

м/Задача 58.

58. Механічне зчеплення - це пристрій, який змінює один тип руху на інший. Найбільш звичний приклад зустрічається в бензиновому двигуні автомобіля, де шатун змінює лінійний рух поршня в круговий рух колінчастого вала. На верхній панелі малюнка зображено механічне зчеплення, винайдене Peaucellier в 1864 році, і незалежно від Lipkin приблизно в той же час. Він складається з шести стрижнів, з'єднаних шарнірами, чотири коротких утворюють ромб. Точка О закріплена в просторі, але апарат вільно обертається близько О. Рух при Р перетворюється в інший рух при\(\text{P}'\) (або навпаки).

Геометрично зв'язок є механічною реалізацією давньої задачі інверсії в колі. Розглядаючи випадок, в якому ромб складений рівно, нехай\(k\) буде відстань від О до точки, де P і\(\text{P}'\) збігаються. Сформуйте коло радіуса\(k\) з його центром на O. Як P і\(\text{P}'\) рухатися всередину і назовні, точки на внутрішній стороні кола завжди відображаються на точках на його зовнішній стороні, такі, що\(rr'=k^2\). Тобто зв'язок - це тип аналогового комп'ютера, який точно вирішує задачу знаходження зворотного числа\(r\). Інверсія в колі має багато чудових геометричних властивостей, розглянутих в H.S.M. Coxeter, Вступ до геометрії, Wiley, 1961. Якщо ручка вставляється через отвір на P і\(\text{P}'\) простежується над геометричною фігурою, зв'язок Peaucellier може бути використана для малювання свого роду зображення фігури.

Пов'язаною проблемою є побудова картинок, на зразок тієї, що знаходиться в нижній панелі малюнка, званих анаморфами. Малюнок стовпчика на папері сильно спотворюється, але при розміщенні відбиваючого циліндра в правильному місці зверху сторінки всередині циліндра утворюється неспотворене зображення. (Широкоформатні технології кіно, такі як Cinemascope, засновані на подібних принципах.)

Покажіть, що зв'язок Peaucellier не перетворюється правильно між зображенням та його анаморфом, і розробити модифіковану версію зв'язку, яка робить. Деякі знання аналітичної геометрії будуть корисними.

n/Задача 59.

59. На малюнку зображена лінза з вигнутими поверхнями, але товщина яких постійна по будь-якій горизонтальній лінії. Використовуйте рівняння лінзмейкера, щоб довести, що ця «лінза» насправді не є лінзою взагалі. (рішення в pdf-версії книги)

60. У звичайних умовах гази мають показники заломлення лише трохи більше, ніж у вакууму\(n=1+\epsilon\),\(\epsilon\) т. Е. Припустимо, що промінь перетинає межу між областю вакууму і областю, в якій знаходиться показник заломлення\(1+\epsilon\). Знайдіть максимальний кут, на який такий промінь може коли-небудь відхилятися, в межі малого\(\epsilon\). \ hwhint {hwhint:дуже слабке заломлення}

61. Сходяться дзеркало має фокусну відстань\(f\). Об'єкт розташовується на відстані\((1+\epsilon)f\) від дзеркала, де\(\epsilon\) невеликий. Знайдіть відстань зображення від дзеркала, максимально спростивши свій результат, скориставшись припущенням,\(\epsilon\) яке невелике. \ hwans {hwans: близька до фокусної довжини}

Contributors and Attributions

Template:ContribCrowell