13.2: Зображення за відображенням

Last updated
Save as PDF

Page ID: 73631

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Немовлята завжди зачаровують витівки Немовляти в Дзеркалі. Тепер, якщо ви хочете знати щось про дзеркальні зображення, що більшість людей не розуміють, спробуйте це. Спочатку наблизите цю сторінку ближче і ближче до очей, поки не зможете більше зосередитися на ній, не напружуючись. Потім зайдіть у ванну кімнату і подивіться, наскільки близько ви зможете підібратися до поверхні дзеркала, перш ніж ви вже не зможете легко зосередитися на зображенні власних очей. Ви виявите, що найкоротша комфортна відстань дзеркала для очей набагато менше, ніж найкоротша комфортна відстань для очей. Це демонструє, що зображення вашого обличчя в дзеркалі діє так, ніби воно мало глибину і існувало в просторі за дзеркалом. Якби зображення було схоже на плоску картинку в книзі, то ви б не змогли зосередитися на ньому з такої невеликої відстані.

У цьому розділі ми вивчимо зображення, сформовані плоскими і вигнутими дзеркалами на якісній, концептуальній основі. Хоча цей тип зображення не так часто зустрічається в повсякденному житті, як зображення, утворені лінзами, зображення, утворені відображенням, легше зрозуміти, тому ми обговорюємо їх спочатку. У розділі 12.3 ми перейдемо до більш математичної обробки зображень, зроблених відображенням. Дивно, але ті ж рівняння можуть бути застосовані і до лінз, які є темою розділу 12.4.

12.2.1 Віртуальний образ

a/Зображення, утворене дзеркалом.

Ми можемо зрозуміти дзеркальне відображення за допомогою променевої діаграми. На малюнку а показано кілька світлових променів, 1, які виникли внаслідок дифузного відображення в носі людини. Вони відскакують від дзеркала, виробляючи нові промені, 2. Для тих, чиє око знаходиться в правильному положенні, щоб отримати один із цих променів, вони, здається, прийшли з-за дзеркала, 3, де вони виникли б з однієї точки. У цій точці з'являється кінчик образу-носа людини. Подібний аналіз стосується будь-якої іншої точки на обличчі людини, тому виглядає так, ніби за дзеркалом було ціле обличчя. Звичайний спосіб опису ситуації вимагає деякого пояснення:

Звичайний опис у фізиці: За дзеркалом є зображення обличчя.
Переклад: Візерунок променів, що йдуть від дзеркала, точно такий же, як би за дзеркалом знаходилося обличчя. Нічого насправді немає за дзеркалом.

Це називається віртуальним зображенням, тому що промені насправді не перетинаються в точці за дзеркалом. Вони, здається, виникли лише там.

самостійна перевірка:

Уявіть, що людина в фігурі а зовсім трохи рухає обличчям вниз — на пару футів у реальному житті, або на кілька дюймів на цьому малюнку масштабу. Дзеркало залишається там, де воно є. Намалюйте нову діаграму променів. Чи буде ще зображення? Якщо так, то звідки це видно?

(відповідь у зворотному боці PDF-версії книги)

Геометрія дзеркального відображення говорить нам, що промені 1 і 2 знаходяться під рівними кутами до нормалі (уявна перпендикулярна лінія, що пронизує дзеркало в точці відображення). Це означає, що уявне продовження променя 2, 3, утворює той же кут з дзеркалом, що і промінь 1. Оскільки кожен промінь 3 типу утворює з дзеркалом ті ж кути, що і його партнер типу 1, ми бачимо, що відстань зображення від дзеркала таке ж, як і у фактичного особи від дзеркала, і воно лежить прямо навпроти нього. Таким чином, зображення має такий же розмір, як і власне обличчя.

b/ Приклад 2.

Приклад 2: Очний іспит
На малюнку b показана типова установка в оглядовому кабінеті окуліста. Зір пацієнта повинен бути випробуваний на відстані 6 метрів (20 футів у США), але ця відстань більше, ніж кількість вільного місця в кімнаті. Тому дзеркало використовується для створення зображення очної діаграми за стіною.

Приклад 2: Очний іспит

На малюнку b показана типова установка в оглядовому кабінеті окуліста. Зір пацієнта повинен бути випробуваний на відстані 6 метрів (20 футів у США), але ця відстань більше, ніж кількість вільного місця в кімнаті. Тому дзеркало використовується для створення зображення очної діаграми за стіною.

Приклад 3: Праксиноскоп
c/Праксиноскоп. На малюнку c зображено старомодний пристрій під назвою праксиноскоп, який відображає анімовану картинку при закручуванні. Знімна смужка паперу з нанесеними на неї малюнками має вдвічі більший радіус внутрішнього кола, зробленого з плоских дзеркал, тому віртуальне зображення кожного знімка знаходиться в центрі. Коли колесо обертається, зображення кожного знімка замінюється наступним.

Приклад 3: Праксиноскоп

c/Праксиноскоп.

На малюнку c зображено старомодний пристрій під назвою праксиноскоп, який відображає анімовану картинку при закручуванні. Знімна смужка паперу з нанесеними на неї малюнками має вдвічі більший радіус внутрішнього кола, зробленого з плоских дзеркал, тому віртуальне зображення кожного знімка знаходиться в центрі. Коли колесо обертається, зображення кожного знімка замінюється наступним.

Обговорення Питання

◊ На малюнку зображений предмет, який знаходиться на одній стороні дзеркала. Намалюйте діаграму променів. Чи формується образ? Якщо так, то де це, і з яких напрямків було б видно?

12.2.2 Вигнуті дзеркала

Зображення в плоскому дзеркалі - дотехнологічний приклад: навіть тварини можуть дивитися на свої відображення в спокійному водоймі. Тепер перейдемо до нашого першого нетривіального прикладу маніпуляції зображенням за технологією: зображення в вигнутому дзеркалі. Перш ніж зануритися, давайте розглянемо, чому це важливий приклад. Якби мова йшла лише про запам'ятовування купи фактів про вигнутих дзеркалах, то ви б справедливо повстали проти спроби зіпсувати красу свого рясно освіченого мозку силою підживлюючи вас технологічними дрібницями. Причина цього є важливим прикладом не в тому, що вигнуті дзеркала настільки важливі самі по собі, а в тому, що результати, які ми отримуємо для криволінійних дзеркал у формі чаші, виявляються вірними для великого класу інших оптичних пристроїв, включаючи дзеркала, які випирають назовні, а не всередину, а також лінзи. Мікроскоп або телескоп - це просто комбінація лінз або дзеркал або обох. Те, про що ви дійсно дізнаєтеся тут, є основним будівельним блоком всіх оптичних пристроїв від кінопроекторів до очей восьминога.

d/ Зображення, утворене вигнутим дзеркалом.

Оскільки дзеркало на малюнку d вигнуте, воно згинає промені назад ближче один до одного, ніж плоске дзеркало: ми описуємо його як сходяться. Зверніть увагу, що термін відноситься до того, що він робить зі світловими променями, а не до фізичної форми поверхні дзеркала. (Сама поверхня буде описана як увігнута. Термін не все, що важко запам'ятати, тому що видовблений інтер'єр дзеркала схожий на печеру.) Дивно, але правда, що всі промені, як 3, дійсно сходяться на точці, утворюючи хороший образ. Ми не будемо доводити цей факт, але це вірно для будь-якого дзеркала, кривизна якого досить ніжна і симетрична щодо обертання навколо перпендикулярної лінії, що проходить через його центр (не асиметрична, як картопляна стружка). Старомодний метод виготовлення дзеркал та лінз - це шліфування їх у зернистості вручну, і це автоматично має тенденцію до отримання майже ідеальної сферичної поверхні.

Згинання променя, як 2 всередину, передбачає вигин його уявного продовження 3 назовні, так само, як підняття одного кінця гойдалки змушує інший кінець опускатися вниз. Тому зображення формується глибше за дзеркалом. Це не просто показує, що є додаткова відстань між зображенням-носом і дзеркалом; це також означає, що саме зображення більше спереду назад. Він був збільшений у напрямку спереду назад.

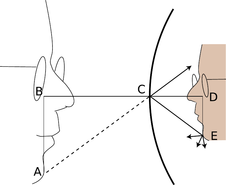
e/Зображення збільшено на той же коефіцієнт по глибині і в інших його розмірах.

Легко довести, що те саме збільшення стосується і інших розмірів зображення. Розглянемо точку, подібну до E на малюнку е., Хитрість полягає в тому, що з усіх променів, дифузно відбитих E, ми вибираємо той, який відбувається з головою до центру дзеркала, C рівнокутна властивість дзеркального відображення плюс трохи прямої геометрії легко призводить нас до висновку, що трикутники ABC і CDE мають однакову форму, причому ABC є просто масштабованою версією CDE. Збільшення глибини дорівнює співвідношенню BC/CD, а збільшення вгору-вниз - AB/DE. Повторення того ж доказу показує, що збільшення в третьому вимірі (поза сторінкою) також однакове. Це означає, що імідж-голова - це просто більша версія реального, без будь-яких спотворень. Коефіцієнт масштабування називається збільшенням,\(M\). Зображення на малюнку збільшено в коефіцієнт\(M=1.9\).

f/Підвищене збільшення завжди відбувається за рахунок зменшеного поля зору.

Зауважте, що ми явно не вказували, чи було дзеркало сферою, параболоїдом або якоюсь іншою формою. Однак ми припустили, що буде сформовано сфокусоване зображення, що не обов'язково буде правдою, наприклад, для дзеркала, яке було асиметричним або дуже глибоко вигнутим.

12.2.3 Справжнє зображення

Якщо ми почнемо з розміщення об'єкта дуже близько до дзеркала, г/1, а потім переміщаємо його все далі і далі, зображення спочатку поводиться так, як ми очікували від нашого повсякденного досвіду з плоскими дзеркалами, відступаючи все глибше і глибше за дзеркало. Однак у певний момент відбувається різка зміна. Коли об'єкт знаходиться більше певної відстані від дзеркала, г/2, зображення з'являється догори дном і перед дзеркалом.

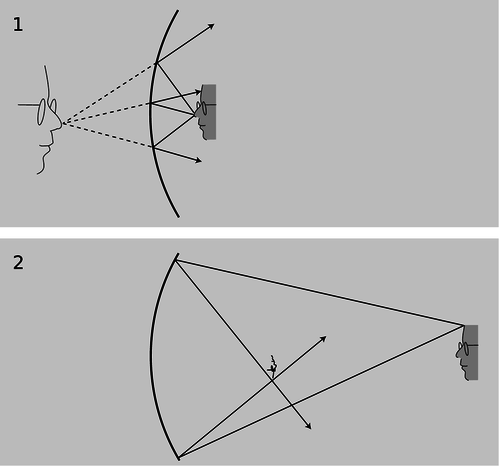
г/1. Віртуальний образ. Справжній образ. Як ви переконаєтеся в домашній задачі 12, зображення перевернуте

Ось що сталося. Дзеркало згинає світлові промені всередину, але коли об'єкт знаходиться дуже близько до нього, як в г/1, промені, що надходять від заданої точки на предмет, занадто сильно розходяться (розтікаються), щоб дзеркало зблизило їх назад. При відображенні промені ще розходяться, тільки не так сильно розходяться. Але коли об'єкт знаходиться досить далеко, г/2, дзеркало лише перехоплює промені, що вийшли у вузькому конусі, і воно здатне зігнути їх досить, щоб вони знову зійшлися.

Зверніть увагу, що промені, зображені на малюнку, які обидва виникли в одній точці на об'єкті, возз'єднуються, коли вони перетинаються. Точка, де вони перетинаються, - це зображення точки на вихідному об'єкті. Цей тип зображення називається реальним зображенням, на відміну від віртуальних зображень, які ми вивчали раніше.

Визначення: Справжнє зображення - це зображення, де насправді перетинаються промені. Віртуальне зображення - це точка, з якої промені, здається, тільки прийшли.

Вживання слова «реальний», мабуть, прикро. Це звучить так, ніби ми говоримо, що зображення було фактичним матеріальним об'єктом, що, звичайно, це не так.

Різниця між реальним зображенням і віртуальним зображенням є важливою, адже реальне зображення може проектуватися на екран або фотоплівку. Якщо в місці розташування зображення вставити аркуш паперу на малюнку г/2, то зображення буде видно на папері (за умови, що об'єкт світлий, а кімната темна). Ваше око використовує лінзу, щоб зробити реальне зображення на сітківці.

самостійна перевірка:

Намалюйте ще одну копію особи на малюнку г/1, ще далі від дзеркала, і намалюйте променеву діаграму. Що сталося з місцем розташування зображення?

(відповідь у зворотному боці PDF-версії книги)

12.2.4 Зображення зображень

Якщо ви зараз носите окуляри, то світлові промені зі сторінки маніпулюють спочатку вашими окулярами, а потім лінзою вашого ока. Можна подумати, що проаналізувати це було б вкрай складно, але насправді це досить легко. У будь-якій серії оптичних елементів (дзеркал або лінз або обох) кожен елемент працює на променях, забезпечених попереднім елементом точно так само, як якщо б зображення, утворене попереднім елементом, було фактичним об'єктом.

h/Ньютонівський телескоп використовується з камерою.

На малюнку h показаний приклад із залученням тільки дзеркал. Ньютонівський телескоп, винайдений Ісааком Ньютоном, складається з великого вигнутого дзеркала, плюс другого плоского дзеркала, яке виводить світло з трубки. (У дуже великих телескопах може бути достатньо місця, щоб помістити камеру або навіть людину всередину трубки, в цьому випадку друге дзеркало не потрібно.) Трубка телескопа не є життєво важливою; це в основному структурний елемент, хоча він також може бути корисним для блокування бродячого світла. Об'єктив був знятий з передньої частини корпусу камери, і для цього налаштування не потрібен. Зверніть увагу, що два промені зразка були проведені паралельно, тому що астрономічний телескоп використовується для перегляду об'єктів, які знаходяться вкрай далеко. Ці дві «паралельні» лінії насправді зустрічаються в певній точці, скажімо, кратер на Місяці, тому вони насправді не можуть бути абсолютно паралельними, але вони паралельні для всіх практичних цілей, оскільки нам доведеться слідувати за ними вгору протягом чверті мільйона миль, щоб дістатися до точки, де вони перетинаються.

i/Ньютонівський телескоп використовується для візуального, а не фотографічного спостереження. У реальному житті лінза окуляра зазвичай використовується для додаткового збільшення, але ця простіша установка також спрацює.

Велике вигнуте дзеркало саме по собі сформувало б зображення\(\text{I}\), але маленьке плоске дзеркало створює зображення\(\text{I}'\). Відносини між\(\text{I}\) і\(\text{I}'\) точно такі ж, як було б, якби\(\text{I}\) був фактичний об'єкт, а не зображення:\(\text{I}\) і\(\text{I}'\) знаходяться на рівних відстанях від площини дзеркала, а лінія між ними перпендикулярна площині дзеркала.

Однією з дивовижних зморшок є те, що в той час як плоске дзеркало, яке використовується саме по собі, формує віртуальне зображення об'єкта, який є реальним, тут дзеркало формує реальний образ віртуального зображення\(\text{I}\). Це показує, як безглуздо було б намагатися запам'ятати списки фактів про те, які види образів утворюються різними оптичними елементами при різних обставин. Вам краще просто намалювати діаграму променів.

j/Кутовий розмір квітки залежить від його відстані від ока.

Хоча головним моментом тут було навести приклад зображення зображення, фігура i також показує цікавий випадок, коли нам потрібно розмежувати збільшення та кутове збільшення. \(\text{I}\)Якщо ви дивитеся на Місяць через цей телескоп, то зображення\(\text{I}\) і\(\text{I}'\) набагато менше, ніж фактична Місяць. Інакше, наприклад, зображення не\(\text{I}\) помістилося б всередину телескопа! Однак ці зображення дуже близькі вашому оку в порівнянні з фактичною місяцем. Невеликий розмір зображення був більш ніж компенсований меншою відстанню. Тут важливим є кількість кута у вашому полі зору, яке охоплює зображення, і саме цей кут був збільшений. Коефіцієнт, за допомогою якого він збільшується, називається кутовим збільшенням,\(M_a\).

k/ Людина використовує дзеркало, щоб отримати вид на обидві сторони сонечка. Хоча плоске дзеркало має\(M=1\), воно не дає кутового збільшення 1. Зображення знаходиться далі від ока, ніж об'єкт, тому кутове збільшення\(M_a=\alpha_i/\alpha_o\) менше одиниці.