11.E: Поля (вправи)
- Page ID
- 73276
1. Зазор між електродами в свічці запалювання автомобільного двигуна становить 0,060 см. Для отримання електричної іскри в бензиново-повітряної суміші необхідно досягти електричного поля\(3.0\times10^6\) В/м. При запуску автомобіля, яке мінімальне напруга має подаватися ланцюгом запалювання? Припустимо, що поле є рівномірним. (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Невеликий розмір зазору між електродами незручний, оскільки він може легко заблокувати, і для його вимірювання потрібні спеціальні інструменти. Чому вони не розробляють свічки запалювання з більш широким зазором?
2. (а) Як запропоновано в прикладі 9 на сторінці 573, використовуйте наближення, щоб показати, що вираз, даний для електричного поля, наближається до\(kQ/d^2\) великого\(d\).
(b) Зробіть те ж саме для результату прикладу 12 на сторінці 577.
3. Астрономи вважають, що розподіл маси (маса на одиницю об'єму) деяких галактик може бути наближений, у сферичних координатах\(\rho=ae^{-br}\)\(0\le r\le\infty\), за, де\(\rho\) щільність. Знайдіть загальну масу.
4. (а) В той час\(t=0\) позитивно заряджена частинка поміщається в спокої у вакуумі, в якому є рівномірне електричне поле величини\(E\). Напишіть рівняння, що дає швидкість частинки\(v\), з точки зору\(t\)\(E\), і її масу і заряд\(m\) і\(q\). (Перевірка відповіді доступна на lightandmatter.com)
(b) Якщо це робиться з двома різними об'єктами, і вони, як спостерігаються, мають однаковий рух, що ви можете зробити висновок про їх маси та заряди? (Наприклад, коли була виявлена радіоактивність, було встановлено, що одна з форм має такий же рух, як електрон у цьому типі експерименту.)
5. Показати, що альтернативне визначення величини електричного поля\(|E|=\tau/D_t\sin\theta\), має одиниці, які мають сенс.
6. Повторіть обчислення прикладу 5 на сторінці 566, використовуючи іншу точку координат для системи координат, і покажіть, що ви отримаєте той самий результат.
7. Визначення дипольного моменту передбачає вектор\(\mathbf{D}=\sum q_i \mathbf{r}_i\), що\(\mathbf{r}_i\) тягнеться від початку нашої системи координат до заряду\(q_i\). Є чіткі випадки, коли це призводить до того, що дипольний момент залежить від вибору системи координат. Наприклад, якщо є тільки один заряд, то ми могли б зробити дипольний момент дорівнює нулю, якщо ми вибрали походження бути прямо на вершині заряду, або ненульовий, якщо ми поставимо походження десь ще.
(а) Складіть числовий приклад з двома зарядами однакової величини та протилежним знаком. Обчислити дипольний момент за допомогою двох різних систем координат, які орієнтовані однаково, але відрізняються вибором походження. Прокоментуйте результат.
(б) Узагальнити результат частини а до будь-якої пари зарядів з рівною величиною і протилежним знаком. Це повинно бути доказом будь-якого розташування двох зарядів, тому не припускайте жодних цифр.
(c) Узагальнити далі, до\(n\) звинувачень.
9. Знайдіть розташування зарядів, які мають нульовий загальний заряд і нульовий дипольний момент, але це зробить незникаючі електричні поля.
10. Як запропоновано в прикладі 11 на сторінці 575, показати, що ви можете отримати той самий результат для поля на осі, диференціюючи напругу

b/Задача 11.
11. Три заряди розташовані на квадраті, як показано на малюнку. Всі три заряди позитивні. Яке значення\(q_2/q_1\) буде виробляти нульове електричне поле в центрі квадрата? (Перевірка відповіді доступна на сайті lightandmatter.com)
12. Це одновимірна проблема, при цьому все обмежується\(x\) віссю. Диполь А складається з заряду\(-1.000\) С при\(x=0.000\) м і заряду\(1.000\) С при\(x=1.000\) м. диполь B має заряд\(-2.000\) C при\(x=0.000\) m і\(2.000\) C заряду при\(x=0.500\) м.
(а) Порівняйте два дипольних моменти.
(b) Обчисліть поле, створене\(x=10.000\) диполем A на m, і порівняти з полем диполь B зробить. Прокоментуйте результат. (Перевірка відповіді доступна на сайті lightandmatter.com)
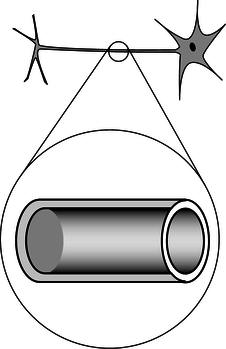
c/Задача 13.
13. У нашому тепер знайомому нейроні різниця напруг між внутрішньою і зовнішньою поверхнями клітинної мембрани знаходиться приблизно\(V_{out}-V_{in}=-70\ \text{mV}\) в стані спокою, а товщина мембрани становить близько 6,0 нм (тобто товщиною всього близько ста атомів). Що таке електричне поле всередині мембрани? (Перевірка відповіді доступна на сайті lightandmatter.com)
14. Протон знаходиться в області, в якій задано електричне поле\(E=a+bx^3\). Якщо протон починається в стані спокою\(x_1=0\), знайдіть його швидкість\(v\), коли він досягне положення\(x_2\). Дайте свою відповідь з точки зору\(a\)\(b\),\(x_2\),\(e\) і\(m\), і, заряд і маса протона. (Перевірка відповіді доступна на сайті lightandmatter.com)
15. (а) Враховуючи, що на осі поле диполя на великих відстанях пропорційно\(D/r^3\), показати, що його напруга змінюється як\(D/r^2\). (Ігнорувати позитивні і негативні ознаки і числові константи пропорційності.)
(b) Запишіть точний вираз для напруги двозарядного диполя в точці на осі, не припускаючи, що відстань велика порівняно з розміром диполя. Ваш вираз повинен містити фактичні заряди та розмір диполя, а не лише його дипольний момент. Тепер використовуйте наближення, щоб показати, що на великих відстанях це відповідає вашій відповіді на частину a.\ hwhint {hwhint:dipolev}
16. Атом водню електрично нейтральний, тому на великих відстанях ми очікуємо, що він створить по суті нульове електричне поле. Це невірно, однак, поблизу атома або всередині нього. Дуже близько до протона, наприклад, поле дуже сильне. Щоб побачити це, подумайте про електрон як сферично симетричну хмару, яка оточує протон, стає все тоншим і тоншим, коли ми віддаляємось від протона. (Квантова механіка говорить нам, що це більш правильна картина, ніж спроба уявити електрон, що обертається навколо протона.) Поруч з центром атома поле електронної хмари скасовується симетрією, але поле протона сильне, тому загальне поле дуже сильне. Напруга в атомі водню і навколо нього можна наблизити за допомогою виразу форми\(V=r^{-1}e^{-r}\). (Одиниці виходять неправильно, тому що я залишив деякі константи.) Знайдіть електричне поле, відповідне цій напрузі, і прокоментуйте його поведінку при дуже великому і дуже маленькому\(r\). (рішення в pdf-версії книги)
17. Молекула вуглекислого газу структурована як O-C-O, з усіма трьома атомами вздовж лінії. Атоми кисню захоплюють трохи додаткового негативного заряду, залишаючи вуглець позитивним. Симетрія молекули, однак, означає, що вона не має загального дипольного моменту, на відміну від V-подібної молекули води, наприклад. Тоді як напруга диполя\(D\) величини пропорційно\(D/r^2\) (див. Задача 15), то виходить, що напруга молекули вуглекислого газу в віддаленій точці вздовж осі молекули дорівнює\(b/r^3\), де\(r\) відстань від молекули і\(b\) константа (див. завдання 9). Яким буде електричне поле молекули вуглекислого газу в точці на осі молекули, на відстані\(r\) від молекули? (Перевірка відповіді доступна на сайті lightandmatter.com)
18. Атом водню в певному стані має щільність заряду (заряд на одиницю об'єму) електронної хмари\(\rho=ae^{-br}z^2\), заданої, де\(r\) відстань від протона, і координата\(z\), виміряна вздовж\(z\) осі. З огляду на, що сумарний заряд електронної хмари повинен бути\(-e\), знайдіть\(a\) в терміні інші змінні.
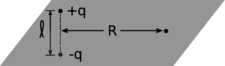
d/Задача 19.
19. Диполь має середню площину, тобто площину, яка прорізає центр диполя, і перпендикулярна осі диполя. Розглянемо двозарядний диполь, зроблений з точкових зарядів,\(\pm q\) розташованих в\(z=\pm\ell/2\). Використовуйте наближення, щоб знайти поле у віддаленій точці на середній площині, і показати, що його величина виходить рівною\(kD/R^3\) (половина того, що було б у точці на осі, що лежить на рівній відстані від диполя).

e/Задача 20.
20. На малюнку зображена вакуумна камера, оточена чотирма металевими електродами у формі гіперболи. (Так, фізики іноді запитують свої університетські верстати про речі, оброблені в математичних формах, як це. Вони повинні бути виготовлені на станах, керованих комп'ютером.) Припускаємо, що електроди простягаються далеко в сторінку і з неї уздовж\(z\) невидимої осі, так що по симетрії електричні поля однакові для всіх\(z\). Тому проблема є ефективною двовимірною. Два електроди знаходяться під напругою\(+V_\text{o}\), а інші два при\(-V_\text{o}\), як показано на малюнку. Рівняння гіперболічних поверхонь є\(|xy|=b^2\), де\(b\) константа. (Ми можемо інтерпретувати\(b\) як надання місць\(x=\pm b\),\(y=\pm b\) чотирьох точок на поверхнях, найближчих до центральної осі.) Немає очевидного пішохідного способу визначити поле або напругу в центральній вакуумній області, але є хитрість, яка працює: з невеликим математичним розумінням ми бачимо, що напруга\(V=V_\text{o}b^{-2}xy\) узгоджується з усією наданою інформацією. (Математики могли б довести, що це рішення було унікальним, але фізик знає це за фізичними ознаками: якби було два різні рішення, не було б фізичного способу вирішити, який з них робити!) (a) Використовуйте методи підрозділу 10.2.2, щоб знайти поле у вакуумній області, і (б) намалюйте поле як «море стріл». (Перевірка відповіді доступна на сайті lightandmatter.com)
21. (а) Певна область тривимірного простору має напругу\(V=br^2\), яка змінюється як, де\(r\) знаходиться відстань від початку. Використовуйте прийоми підрозділу 10.2.2, щоб знайти поле. (Перевірка відповіді доступна на lightandmatter.com)
(б) Запишіть іншу напругу, яка дає точно таке ж поле.
22. (a) Приклад 10 на сторінці 574 дає поле зарядженого стрижня в його середній площині. Відштовхуючись від цього результату, візьміть межу, оскільки довжина стрижня наближається до нескінченності. Зверніть увагу,\(\lambda\) що не змінюється, так як\(L\) стає більше, загальний заряд\(Q\) збільшується. \ hwans {hwans: estrips}
(b) У тексті я показав (кількома різними методами), що поле нескінченної, рівномірно зарядженої площини є\(2\pi k\sigma\). Тепер ви збираєтеся отримати той же результат іншим методом. Припустимо, що це\(x-y\) площина, яка заряджена, і ми хочемо знайти поле в точці\((0,0,z)\). (Оскільки площина нескінченна, немає втрати спільності в припущенні\(x=0\) і\(y=0\).) Уявімо, що ми розрізаємо площину на нескінченну кількість прямих смуг, паралельних\(y\) осі. Кожна смуга має нескінченно малу ширину\(dx\), і простягається від\(x\) до\(x+dx\). Внесок будь-якої з цих смужок в поле в нашій точці має величину, яку можна знайти з частини а. шляхом векторного додавання довести бажаний результат для поля площини заряду.

f/Задача 23.
23. Розглянемо електричне поле, створене рівномірно зарядженої циліндричної поверхнею, яка простягається до нескінченності в одному напрямку.
(а) Покажіть, що поле в центрі гирла циліндра є\(2\pi k\sigma\), яке буває таким же, як поле нескінченного плоского аркуша заряду!
(б) Цей вираз не залежить від радіуса циліндра. Поясніть, чому так повинно бути. Наприклад, що буде, якщо ви подвоїте радіус циліндра?
24. Під час електричної бурі хмара і земля діють як конденсатор з паралельною пластиною, який зазвичай заряджається через фрикційну електрику при зіткненнях частинок льоду в холодній верхній атмосфері. Блискавка виникає, коли величина електричного поля наростає до критичної величини\(E_c\), при якій повітря іонізується.
(а) Обробляйте хмару як плоский квадрат зі сторонами довжини\(L\). Якщо він знаходиться на висоті\(h\) над землею, знайдіть кількість енергії, що виділяється при ударі блискавки. (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) На основі вашої відповіді з частини а, яка є більш небезпечною, удар блискавки з висотної хмари або низьковисотний?
(c) Зробіть оцінку на порядок величини енергії, що виділяється типовим блискавкою, припускаючи розумні значення для його розміру та висоти. \(E_c\)становить близько\(10^6\) В/м.
25. (а) Покажіть, що енергія в електричному полі точкового заряду нескінченна! Чи розходиться інтеграл на малих відстанях, на великих відстанях або обох? \ hwhint {hwhint:epointinfty}
[4] (b) Тепер обчислимо енергію в електричному полі рівномірно зарядженої сфери з радіусом\(b\). Виходячи з теореми оболонки, можна показати, що поле for\(r>b\) таке ж, як і для точкового заряду, тоді як поле для\(r\lt b\) -\(kqr/b^3\). (Приклад 38 показує це за допомогою іншої техніки.)
(Перевірка відповіді доступна на сайті lightandmatter.com)

g/Задача 26.
26. Нейрон на малюнку був намальований досить коротко, але деякі нейрони у вашому спинному мозку мають хвости (аксони) довжиною до метра. Внутрішня і зовнішня поверхні мембрани виступають в ролі «пластин» конденсатора. (Той факт, що він був згорнутий в циліндр, дуже мало впливає.) Для того щоб функціонувати, нейрон повинен створити різницю напруг\(V\) між внутрішньою і зовнішньою поверхнями мембрани. Нехай товщина мембрани, радіус, і довжина буде\(t\)\(r\), і\(L\). (а) Обчисліть енергію, яка повинна зберігатися в електричному полі, щоб нейрон виконував свою роботу. (У реальному житті мембрана зроблена з речовини, званої діелектриком, електричні властивості якого збільшують кількість енергії, яку необхідно зберігати. Заради цього аналізу проігноруйте цей факт.) \ hwhint {hwhint:neuronenergy} (перевірка відповіді доступна на сайті lightandmatter.com)
(б) Еволюційна придатність організму повинна бути кращою, якщо йому потрібно менше енергії для роботи своєї нервової системи. Виходячи з вашої відповіді на частину а, що б ви очікували, що еволюція зробить з вимірами\(t\) і\(r?\) Які інші обмеження утримають ці еволюційні тенденції від занадто далеко?

h/Задача 27.
27. На малюнку показані види поперечного перерізу двох кубічних конденсаторів, і вид поперечного перерізу тих же двох конденсаторів, зібраних разом так, щоб їх інтер'єри збігалися. Конденсатор з пластинами близько один до одного має майже рівномірне електричне поле між пластинами, і майже нульове поле зовні; ці конденсатори не мають своїх пластин дуже близько один до одного порівняно з розмірами пластин, але для цілей цієї проблеми припустимо, що вони все ще мають приблизно вид ідеалізованого поля візерунок, показаний на малюнку. Кожен конденсатор має внутрішній об'єм 1,00 і заряджається до того моменту\(\text{m}^3\), коли його внутрішнє поле становить 1,00 В/м.
(а) Обчисліть енергію, що зберігається в електричному полі кожного конденсатора, коли вони розділені. (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Обчисліть величину внутрішнього поля, коли два конденсатори зібрані разом у спосіб, показаний. Ігнорувати ефекти, що виникають при перерозподілі заряду кожного конденсатора під впливом іншого конденсатора. (Перевірка відповіді доступна на сайті lightandmatter.com)
(c) Обчисліть енергію складеної конфігурації. Чи збирають їх, як це вивільняють енергію, споживають енергію, чи ні? (Перевірка відповіді доступна на сайті lightandmatter.com)
28. Знайдіть ємність поверхні землі, припускаючи, що на нескінченності є зовнішня сферична «тарілка». (Насправді ця зовнішня пластина просто представляла б якусь віддалену частину Всесвіту, до якої ми захопили частину земного заряду, щоб зарядити землю.) (Перевірка відповіді доступна на сайті lightandmatter.com)
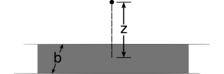
i/Задача 29.
29. (a) Показати, що поле, знайдене в прикладі 10 на сторінці 574, зменшується до\(E=2k\lambda/R\) межі\(L\rightarrow\infty\).
(б) Нескінченна смуга ширини\(b\) має поверхневу щільність заряду\(\sigma\). Знайдіть поле в точці на відстані\(z\) від смуги, що лежить в площині перпендикулярно розсікає смугу. (перевірка відповіді доступна на сайті lightandmatter.com)
(c) Показати, що цей вираз має правильну поведінку в межі, де\(z\) наближається до нуля, а також в межі\(z\gg b\). Для останнього вам знадобиться результат завдання 22 а, який наведено на сторінці 930.
30. Твердий циліндр радіусу\(b\) і довжини\(\ell\) рівномірно заряджений загальним зарядом\(Q\). Знайдіть електричне поле в точці в центрі одного з плоских кінців.
31. Знайдіть напругу на краю рівномірно зарядженого диска. (Визначте,\(V=0\) щоб бути нескінченно далеко від диска.) (перевірка відповіді доступна на сайті lightandmatter.com)\ hwhint {hwhint:vedgedisk}
32. Знайдіть енергію, що зберігається в конденсаторі, з точки зору його ємності та різниці напруг на ньому. (Перевірка відповіді доступна на сайті lightandmatter.com)
33. (а) Знайти ємність двох однакових конденсаторів послідовно.
(б) Виходячи з цього, як би ви очікували, що ємність конденсатора паралельної пластини залежатиме від відстані між пластинами?
34. (а) Використовуйте методи складних чисел, щоб переписати функцію\(f(t)=4\sin\omega t+3\cos\omega t\) у формі\(A\sin(\omega t+\delta)\). (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Перевірте результат за допомогою тригонометричної ідентичності\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\).
35. (а) Показати, що рівняння\(V_L=LdI/dt\) має правильні одиниці.
(b) Переконайтеся, що\(RC\) має одиниці часу.
(c) Переконайтеся, що\(L/R\) має одиниці часу.
36. Знайдіть індуктивність двох однакових індукторів паралельно.
37. Обчисліть величину\(i^i\) (тобто знайти її реальну і уявну частини). (Перевірка відповіді доступна на сайті lightandmatter.com)
38. Самі дроти в ланцюзі можуть мати опір, індуктивність і ємність. Чи буде «бродяча» індуктивність та ємність найважливішими для низькочастотних або для високочастотних ланцюгів? Для простоти припустимо, що дроти діють так, як вони послідовно з індуктором або конденсатором.
39. Починаючи з співвідношення різниці напруги\(V=LdI/dt\) на індукторі, показати, що індуктор має імпеданс, рівний\(L\omega\).
40. Прямокутна коробка рівномірно заряджена щільністю заряду\(\rho\). Коробка надзвичайно довга і худа, а її перетин - квадрат зі сторонами довжини\(b\). Довжина настільки велика в порівнянні з тим\(b\), що ми можемо вважати її нескінченною. Знайдіть електричне поле в точці, що лежить на поверхні коробки, в середній точці між двома краями. Ваша відповідь буде включати інтеграл, який найбільш легко зробити за допомогою комп'ютерного програмного забезпечення.
41. Порожниста циліндрична труба має довжину\(\ell\) і радіус\(b\). Його кінці відкриті, але на криволінійної поверхні він має щільність заряду\(\sigma\). Заряд\(q\) з масою\(m\) вивільняється в центрі труби, в нестійкому рівновазі. Оскільки рівновага нестабільна, частинка прискорюється в ту чи іншу сторону, вздовж осі труби, і виходить, як куля зі стовбура гармати. Знайти швидкість частинки, коли вона знаходиться нескінченно далеко від «гармати». Ваша відповідь буде включати інтеграл, який важко зробити вручну; Ви можете подивитися його в таблиці інтегралів, зробити це в Інтернеті на integrals.com, або завантажити та встановити безкоштовне символічне математичне програмне забезпечення Maxima від maxima.sourceforge.net.
42. Якщо FM-радіо тюнер, що складається з ланцюга LRC містить 1,0\(\mu\text{H}\) індуктор, який діапазон ємностей повинен бути в змозі забезпечити змінний конденсатор? (Перевірка відповіді доступна на сайті lightandmatter.com)
43. (а) Знайдіть паралельний імпеданс\(37\ \text{k}\Omega\) резистора та конденсатора 1.0 нФ на\(f=1.0\times10^4\) частоті Гц. (Перевірка відповіді доступна на lightandmatter.com)
(b) Напруга з амплітудою 1,0 мВ керує цим імпедансом на цій частоті. Яка амплітуда струму, витягнутого від джерела напруги, який кут фази струму по відношенню до напруги, і веде він напругу, або відстає від нього? (Перевірка відповіді доступна на сайті lightandmatter.com)
44. Ланцюг серії LRC складається з\(\Omega\) резистора 1.000, конденсатора 1.000 F та індуктора 1.000 H. (Це не особливо прості значення, щоб знайти на полиці в Radio Shack!)
(а) Побудувати його імпеданс як точку в комплексній площині для кожної з наступних частот:\(\omega\) = 0.250, 0.500, 1.000, 2.000 і 4.000 Гц.
(б) Що таке резонансна кутова частота\(\omega_{res}\), і як це пов'язано з вашим сюжетом? (Перевірка відповіді доступна на lightandmatter.com)
(c) Яка резонансна частота\(f_{res}\) відповідає вашій відповіді в частині b? (Перевірка відповіді доступна на сайті lightandmatter.com)
45. На\(\omega\) частоті певна серія LR ланцюга має імпеданс\(1\ \Omega+(2\ \Omega)i\). Припустимо, що замість цього ми хочемо досягти однакового імпедансу, використовуючи два елементи схеми паралельно. Якими повинні бути елементи?
46. (a) Використовуйте закон Гауса, щоб знайти поля всередині і зовні нескінченної циліндричної поверхні з радіусом\(b\) і рівномірною поверхневою щільністю заряду\(\sigma\). (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Показати, що в електричному полі є розрив, рівний\(4\pi k \sigma\) між однією стороною поверхні та іншою, як і повинно бути (див. Стор. 628).
(c) Reexpress ваш результат з точки зору заряду на одиницю довжини, і порівняти з полем лінії заряду.
(г) Коаксіальний кабель має два провідники: центральний провідник\(a\) радіусу та зовнішній провідник радіусу\(b\). Ці два провідника розділені ізолятором. Хоча такий кабель зазвичай використовується для сигналів, що змінюються в часі, припустимо протягом всієї цієї проблеми, що між двома провідниками просто постійна напруга. Зовнішній провідник тонкий, як і в частині c Внутрішній провідник твердий, але, як завжди буває у провідника в електростатиці, заряд зосереджений на поверхні. Таким чином, ви можете знайти всі поля в частині b, накладаючи поля, належні кожному провіднику, як це знайдено в частині c. (Зверніть увагу, що на заданій довжині кабелю сумарний заряд внутрішнього і зовнішнього провідників дорівнює нулю\(\lambda_1=-\lambda_2\)\(\sigma_1\ne\sigma_2\), так як площі нерівні.) Знайдіть ємність на одиницю довжини такого кабелю. (Перевірка відповіді доступна на сайті lightandmatter.com)
47. У певній області простору електричне поле постійне (тобто вектор завжди має однакову величину і напрямок). Для простоти припустимо, що поле вказує в позитивну\(x\) сторону. (а) Використовуйте закон Гаусса, щоб довести, що в цій області космосу немає жодної плати. Це найпростіше зробити, розглянувши гаусову поверхню, що складається з прямокутної коробки, краї якої паралельні\(x\)\(y\), і\(z\) осей.
(b) Якщо в цій області простору немає зарядів, що може зробити це електричне поле?
48. (а) У послідовному ланцюзі LC, керованому напругою постійного струму (\(\omega=0\)), порівняйте енергію, що зберігається в індукторі, з енергією, що зберігається в конденсаторі.
(b) Проведіть те саме порівняння для LC-ланцюга, який вільно коливається (без будь-якої рушійної напруги).
(c) Тепер розглянемо загальний випадок послідовного LC-ланцюга, керованого коливальною напругою на довільній частоті. Дозволяти\(\overline{U_L}\) і бути середньою енергією, що зберігається в індукторі, і аналогічно для\(\overline{U_C}\). Визначте величину\(u=\overline{U_C}/(\overline{U_L}+\overline{U_C})\), яку можна інтерпретувати як середню частку енергії конденсатора, тоді як середня\(1-u\) частка індуктора. Знайти з\(u\) точки зору\(L\)\(C\), і\(\omega\), і ескіз графіка\(u\) і\(1-u\) проти\(\omega\). Що відбувається при резонансі? Переконайтеся, що ваш результат відповідає вашій відповіді на частину а. (перевірка відповіді доступна на lightandmatter.com)
49. Використовуйте закон Гауса, щоб знайти поле всередині нескінченного циліндра з радіусом\(b\) і рівномірною щільністю заряду\(\rho\). (Зовнішнє поле має ту ж форму, що і в задачі 46.) (Перевірка відповіді доступна на сайті lightandmatter.com)
50. (а) У певній області простору електричне поле задається\(\mathbf{E}=bx\hat{\mathbf{x}}\), де\(b\) є постійною. Знайдіть кількість заряду, що міститься в кубічному об'ємі\(x=a\), що\(x=0\) поширюється від\(y=0\) до\(y=a\), від до і від\(z=0\) до\(z=a\).
(б) Повторіть для\(\mathbf{E}=bx\hat{\mathbf{z}}\).
(c) Повторіть для\(\mathbf{E}=13bz\hat{\mathbf{z}}-7cz\hat{\mathbf{y}}\).
(г) Повторіть для\(\mathbf{E}=bxz\hat{\mathbf{z}}\).
51. Світло - це хвиля з електричних і магнітних полів, і поля перпендикулярні напрямку руху хвилі, тобто вони поперечні. Прикладом може бути електричне поле, задане\(\mathbf{E}=b \hat{\mathbf{x}} \sin cz\), де\(b\) і\(c\) є константами. (Було б також пов'язане магнітне поле.) Ми спостерігаємо, що світло може подорожувати через вакуум, тому ми очікуємо, що ця хвиля відповідає неіснуванню будь-якого заряду в просторі, який він зараз займає. Скористайтеся законом Гаусса, щоб довести, що це правда.
52. Це альтернативний підхід до проблеми 49, використовуючи іншу техніку. Припустимо, що довгий циліндр містить рівномірну щільність заряду\(\rho\) по всьому своєму внутрішньому об'єму.
(а) Використовуйте методи розділу 10.7, щоб знайти електричне поле всередині циліндра. (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Розширте своє рішення на зовнішній регіон, використовуючи ту саму техніку. Як тільки ви знайдете загальну форму розчину, відрегулюйте його так, щоб внутрішнє і зовнішнє поля збігалися на поверхні. (Перевірка відповіді доступна на сайті lightandmatter.com)
53. Мета цієї домашньої задачі полягає в тому, щоб довести, що розбіжність є інваріантною щодо перекладів. Тобто, не має значення, де ви вирішите поставити початок вашої системи координат. Припустимо, у нас є поле форми\(\mathbf{E}=ax\hat{\mathbf{x}}+by\hat{\mathbf{y}}+cz\hat{\mathbf{z}}\). Це найзагальніше поле, яке ми повинні розглянути в будь-якому невеликому регіоні, що стосується розбіжності. (Залежність від\(x\)\(y\), і\(z\) є лінійною, але будь-яка плавна функція виглядає лінійною крупним планом. Нам також не потрібно ставити такі терміни\(x\hat{\mathbf{y}}\), як, тому що вони не сприяють розбіжності.) Визначте новий набір координат,\((u,v,w)\)\((x,y,z)\) пов'язаних з
де\(p\)\(q\), і\(r\) є константами. Показати, що розбіжність поля однакова в цих нових координатах. Зверніть увагу, що\(\hat{\mathbf{x}}\) і\(\hat{\mathbf{u}}\) ідентичні, і аналогічно для інших координат.
54. Використовуючи методи, подібні до проблеми 53, показують, що розбіжність є обертально інваріантною, в особливому випадку обертань навколо\(z\) осі. При такому обертанні ми обертаємося до нової системи\((u,v,z)\) координат, осі якої повертаються на кут\(\theta \) по відношенню до таких\((x,y,z)\) системи. Координати пов'язані
Знайдіть, як\(u\) і\(v\) компоненти поля\(\mathbf{E}\) залежать від\(u\) і\(v\), і показати, що його розбіжність однакова в цій новій системі координат.
55. Електричне поле задається в циліндричних координатах\((R,\phi,z)\) шляхом\(E_R=ce^{-u|z|}R^{-1}\cos^2\phi\), де позначення\(E_R\) позначають складову поля, спрямовану безпосередньо від осі, а складові в інших напрямках дорівнюють нулю. (Це не зовсім неможливий вираз для поля біля радіопередавальної антени.) (а) Знайдіть загальний заряд, укладений у нескінченно довгому циліндрі, що простягається від осі до\(R=b\). (б) Інтерпретувати\(R\) -залежність вашої відповіді до частини а.
56. Використовуйте теорему Ейлера, щоб вивести теореми про додавання, які виражають\(\sin(a+b)\) і з\(\cos(a+b)\) точки зору синусів і косинусів\(a\) і\(b\). (рішення в pdf-версії книги)
57. Знайти кожне комплексне число\(z\) таке, що\(z^3=1\). (рішення в pdf-версії книги)
58. Помножте вираз\(x^3-y^3\) на множники мінімально можливого порядку, використовуючи комплексні коефіцієнти. (Підказка: використовуйте результат задачі 57.) Потім виконайте те ж саме, використовуючи реальні коефіцієнти. (рішення в pdf-версії книги)

