11.5: Ланцюги LRC

Довга дорога, що веде від лампочки до комп'ютера, почалася з одного дуже важливого кроку: впровадження зворотного зв'язку в електронні схеми. Хоча принцип зворотного зв'язку був зрозумілий і застосований до механічних систем протягом століть, а до електричних з початку ХХ століття, для більшості з нас це слово викликає образ Джимі Хендрікса (або якогось більш пізнього гітарного героя), навмисно створюючи вушні скрипи, або директор школи робить те ж саме ненавмисно в залі для глядачів. У прикладі гітари музикант стоїть перед підсилювачем і повертає його настільки високо, що звукові хвилі, що надходять від динаміка, повертаються до гітарної струни і змушують її трясти сильніше. Це приклад позитивного зворотного зв'язку: чим сильніше вібрує струна, тим сильніше звукові хвилі, і чим сильніше звукові хвилі, тим сильніше вібрує струна. Єдина межа - потужність керованості підсилювача.

Негативні відгуки не менш важливі. Наприклад, ваш термостат забезпечує негативний зворотний зв'язок, виганяючи обігрівач, коли будинок стає досить теплим, і знову розпалюючи його, коли стає занадто холодно. Це призводить до того, що температура будинку коливається вперед і назад в певному діапазоні. Подібно до того, як експоненціальні виродки поза контролем є характерною поведінкою систем позитивного зворотного зв'язку, коливання характерні у випадках негативного зворотного зв'язку. Ви вже широко вивчали негативні відгуки в розділі 3.3 у випадку механічної системи, хоча ми так не називали.

Ємність і індуктивність

При механічному коливанні енергія обмінюється повторно між потенційною та кінетичною формами, а також може бути відключена у вигляді тепла, що розсіюється тертям. В електричному ланцюзі резистори - це елементи ланцюга, які розсіюють тепло. Які електричні аналоги зберігання і вивільнення потенційної і кінетичної енергії вібруючого об'єкта? Коли ви думаєте про накопичення енергії в електричному ланцюзі, ви, ймовірно, уявляєте собі акумулятор, але навіть акумуляторні батареї можуть пройти лише 10 або 100 циклів, перш ніж вони зносяться. Крім того, акумулятори не здатні обмінюватися енергією на досить короткій шкалі часу для більшості застосувань. Схема в музичному синтезаторі може бути викликана коливатися тисячі разів на секунду, і ваша мікрохвильова піч працює на гігагерцових частотах. Замість батарей ми зазвичай використовуємо конденсатори та індуктори для зберігання енергії в коливальних контурах. Конденсатори, з якими ви вже стикалися, зберігають енергію в електричних полах. Індуктор робить те ж саме з магнітними полями.

Конденсатори

Енергія конденсатора існує в навколишніх електричних полах. Вона пропорційна квадрату напруженості поля, яка пропорційна зарядам на пластин. Якщо припустити, що пластини несуть в собі заряди, однакові за величиною,\(+q\) причому\(-q\), то енергія, що зберігається в конденсаторі, повинна бути пропорційною\(q^2\). З історичних причин ми пишемо константу пропорційності як\(1/2C\),

\[\begin{equation*} U_C = \frac{1}{2C}q^2 . \end{equation*}\]

Константа\(C\) - це геометрична властивість конденсатора, зване його ємністю.

a/ Символ конденсатора.

b/ Деякі конденсатори.

Виходячи з цього визначення, одиниці ємності повинні бути кулонами в квадраті на джоуль, і це поєднання зручніше скорочувати як фарад,\(1\ \text{F}=1\ \text{C}^2/\text{J}\). «Конденсатор» - менш формальний термін для конденсатора. Зверніть увагу, що етикетки, надруковані на конденсаторах\(\mu\text{F}\), часто використовують MF для означають, хоча MF дійсно повинен бути символом для мегафарад, а не мікрофарад. Плутанина не є результатом цього нестандартного позначення, оскільки значення пікофарад і мікрофарад є найбільш поширеними, і лише в 1990-х роках навіть значення міліфарад і фарад стали доступні в практичних фізичних розмірах. На малюнку a показано символ, який використовується в схемах для представлення конденсатора.

Приклад\(\PageIndex{1}\): A parallel-plate capacitor

Припустимо, конденсатор складається з двох паралельних металевих пластин з площею\(A\), а зазор між ними є\(h\). Зазор невеликий в порівнянні з розмірами плит. Що таке ємність?

Рішення

Оскільки пластини металеві, заряди на кожній пластині вільно рухаються, і, як правило, щільніше скупчуються біля країв через взаємне відштовхування інших зарядів в тій же пластині. Однак виявляється, що якщо зазор невеликий, це невеликий ефект, тому ми можемо піти з припущення рівномірної щільності заряду на кожній пластині. Результат прикладу 14 потім застосовується, а для області між пластинами ми маємо

\[E=4\pi k\sigma=4\pi kq/ A\]

і

\[U_{e} = (1/8\pi k) E^2 Ah.\]

Підставивши перший вираз в друге, знаходимо\(U_{e}=2\pi kq^2 h/ A\). Порівнюючи це з визначенням ємності, ми закінчуємо\(C= A/4\pi kh\).

Індуктори

с/Дві загальні геометрії для індукторів. Циліндрична форма зліва називається соленоїдом.

Будь-який струм створить магнітне поле, тому насправді кожен струмоведучий провід в ланцюзі діє як індуктор! Однак цей тип «бродячої» індуктивності, як правило, незначний, так само, як ми зазвичай можемо ігнорувати блукаючий опір наших проводів і враховувати лише фактичні резистори. Для зберігання будь-якої помітної кількості магнітної енергії зазвичай використовується котушка дроту, розроблена спеціально, щоб бути індуктором. Усі вклади петель у магнітне поле складаються разом, щоб зробити більш сильне поле. На відміну від конденсаторів і резисторів, практичні індуктори легко зробити своїми руками. Можна, наприклад, намотати якийсь дріт навколо короткого дерев'яного дюбеля. Індуктор, як це, у вигляді циліндричної котушки дроту, називається соленоїдом, c, і стилізований соленоїд, d, є символом, що використовується для представлення індуктора в ланцюзі незалежно від його фактичної геометрії.

d/Символ для індуктора.

e/Деякі індуктори.

Скільки енергії зберігає індуктор? Щільність енергії пропорційна квадрату напруженості магнітного поля, яка, в свою чергу, пропорційна струму, що протікає через спіральний дріт, тому енергія, що зберігається в індукторі, повинна бути пропорційною\(I^2\). Пишемо\(L/2\) для константи пропорційності, даючи

\[\begin{equation*} U_L = \frac{L}{2}I^2 . \end{equation*}\]

Як і при визначенні ємності, ми маємо коефіцієнт 1/2, що є чисто питанням визначення. Величина\(L\) називається індуктивністю індуктивності, і ми бачимо, що його одиниці повинні бути джоулями на ампер в квадраті. Ця незграбна комбінація одиниць частіше скорочується як Генрі, 1 Генрі = 1\(\text{J}/\text{A}^2\). Замість того, щоб запам'ятовувати це визначення, має сенс виводити його, коли це необхідно, з визначення індуктивності. Багато людей знають індуктори просто як «котушки» або «дроселі», і не зрозуміють вас, якщо ви посилаєтесь на «індуктор», але вони все одно будуть називатися «індуктивністю»,\(L\) а не «сполученням» або «задушенням!»

Існує згорнута схема наближення для індукторів, як і для конденсаторів. Для конденсатора це означає припущення, що електричні поля повністю внутрішні, так що компоненти взаємодіють лише за допомогою струмів, що протікають через дроти, а не через фізичне перекриття їх полів у просторі. Аналогічно для індуктора наближення згорнутого контуру є припущенням, що магнітні поля повністю внутрішні.

Приклад\(\PageIndex{2}\): Identical inductances in series

Якщо дві індуктори розміщені послідовно, будь-який струм, який проходить через комбінований подвійний індуктор, повинен проходити через обидві його частини. Якщо припустити наближення згорнутого ланцюга, поля двох індукторів не заважають один одному, тому енергія подвоюється для заданого струму. Таким чином, за визначенням індуктивності індуктивність також подвоюється. Загалом, індуктивності послідовно додають, так само, як і опори. Такий же вид міркувань також показує, що індуктивність соленоїда приблизно пропорційна його довжині, припускаючи, що кількість витків на одиницю довжини зберігається постійною. (Це лише приблизно вірно, тому що встановлення двох соленоїдів наскрізно до кінця призводить до того, що поля поза їхніми ротами перекриваються та складаються складним чином. Іншими словами, наближення кускового контуру може бути не дуже хорошим.)

f/Індуктивності послідовно додати.

Приклад\(\PageIndex{3}\): Identical capacitances in parallel

Коли дві однакові ємності розміщені паралельно, будь-який заряд, нанесений на висновки комбінованого подвійного конденсатора, розділиться рівномірно між двома частинами. Електричні поля, що оточують кожен конденсатор, будуть в два рази менше інтенсивності, а отже, зберігають одну чверть енергії. Два конденсатора, кожен з яких зберігає одну чверть енергії, дають половину загального накопичувача енергії. Оскільки ємність обернено пов'язана з накопичувачем енергії, це означає, що однакові ємності паралельно дають подвійну ємність. Загалом, ємності паралельно додають. Це на відміну від поведінки індукторів і резисторів, для яких послідовні конфігурації дають доповнення.

г/Ємності паралельно додати.

Це узгоджується з результатом прикладу 18, який мав ємність одного паралельно-пластинчастого конденсатора, пропорційну площі пластин. Якщо у нас є два паралельно-пластинчастих конденсатора, і ми об'єднаємо їх паралельно і зближаємо їх дуже близько один пліч-о-пліч, ми виготовили один конденсатор з обкладинками подвійної площі, і він має приблизно подвійну ємність, за умови будь-якого порушення скупчено-ланцюга наближення через взаємодія полів, де краю конденсаторів з'єднані між собою.

Індуктивності паралельно і ємності послідовно досліджуються в домашніх завданнях 36 і 33.

Приклад\(\PageIndex{4}\): A variable capacitor

На малюнку h /1 показано побудова змінного конденсатора з двох паралельних півкіл металу. Одна пластина закріплена, в той час як інша може обертатися навколо своєї загальної осі за допомогою ручки. Протилежні заряди на двох плитах притягуються один до одного, і тому прагнуть збиратися в області перекриття. Таким чином, ця область перекриття є єдиною областю, яка ефективно сприяє ємності, а поворот ручки змінює ємність. Проста конструкція може забезпечити лише дуже малі значення ємності, тому на практиці зазвичай використовується банк конденсаторів, підключених паралельно, з усіма рухомими частинами на одному валу.

h/Змінний конденсатор.

Питання для обговорення

◊ Припустимо, що два паралельно пластинчастих конденсатора підключені паралельно, і розміщені дуже близько один до одного, поруч, так що наближення згорнутої схеми не дуже точне. Чи буде отримана ємність занадто маленькою, або занадто великою? Чи могли б ви скрутити схему в іншу форму і зробити ефект навпаки, або зробити ефект зникати? Як щодо випадку двох індукторів послідовно?

◊ Більшість практичних конденсаторів не мають повітряного зазору або вакуумного зазору між пластинами; замість цього вони мають ізоляційну речовину, звану діелектриком. Ми можемо думати про молекули в цій речовині як диполі, які вільно обертаються (принаймні трохи), але які не вільні для переміщення, оскільки це тверда речовина.

i/Обговорення питання B.

На малюнку зображений сильно стилізований і нереальний спосіб візуалізації цього. Ми уявляємо, що всі диполі спочатку повернуті вбік, (1), і що коли конденсатор заряджається, всі вони реагують поворотом через певний кут, (2). (Насправді сцена може бути набагато більш випадковою, а ефект вирівнювання набагато слабкіше.)

Для простоти уявіть, що вставляєте лише один електричний диполь у вакуумний зазор. Для заданої кількості заряду на пластин, як це впливає на кількість енергії, що зберігається в електричному полі? Як це впливає на ємність?

Тепер переробіть аналіз з точки зору механічної роботи, необхідної для того, щоб зарядити пластини.

10.5.2 Коливання

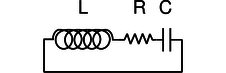
Дж/серія LRC ланцюга.

На малюнку j показаний найпростіший можливий коливальний контур. Для будь-якого корисного додатка насправді потрібно буде включати більше компонентів. Наприклад, якби це був радіотюнер, його потрібно було б підключити до антени і підсилювача. Тим не менш, вся істотна фізика є.

k/ Механічна аналогія для ланцюга LRC.

Ми можемо проаналізувати його без будь-якого поту чи сліз, просто побудувавши аналогію з механічною системою. У механічному осциляторі, k, ми маємо дві форми накопиченої енергії,

\[\begin{align*} U_{spring} &= \frac{1}{2}kx^2 &(1) \\ K &= \frac{1}{2}mv^2 . &(2) \end{align*}\]

У випадку з механічним генератором ми зазвичай припускаємо силу тертя форми, яка, як виявляється, дає найприємніші математичні результати\(F=-bv\). У схемі розсіювання енергії в тепло відбувається через резистор, без участі механічної сили, тому для того, щоб провести аналогію, нам потрібно відновити роль сили тертя з точки зору енергії. Потужність, що розсіюється тертям, дорівнює механічній роботі, яку вона робить за проміжок часу\(dt\), розділений на\(dt\)\(P=W/dt=Fdx/dt=Fv=-bv^2\), так

\[\begin{equation*} \text{rate of heat dissipation} = -bv^2 . (3) \end{equation*}\]

самоперевірка:

Рівняння (1) має\(x\) квадрат, а рівняння (2) і (3) мають\(v\) квадрат. Тому що вони в квадраті, результати не залежать від того, чи є ці змінні позитивними або негативними. Чи має це фізичний сенс? (відповідь у зворотному боці PDF-версії книги)

У ланцюзі накопичені форми енергії

\[\begin{align*} U_C &= \frac{1}{2C}q^2 &(1') \\ U_L &= \frac{1}{2}LI^2 , &(2') \end{align*}\]

а швидкість тепловіддачі в резисторі дорівнює

\[\begin{equation*} \text{rate of heat dissipation} = -RI^2 . (3') \end{equation*}\]

Порівнюючи два множини рівнянь, ми спочатку формуємо аналогії між величинами, які представляють стан системи в якийсь момент часу:

\[\begin{align*} x &\leftrightarrow q\\ v &\leftrightarrow I\\ \end{align*}\]

самоперевірка:

Як математично\(v\) пов'язано\(x\)? Як\(I\) підключений до\(q\)? Чи є ці два відносини аналогічними? (відповідь у зворотному боці PDF-версії книги)

Далі ми віднесемо ті, які описують постійні характеристики системи:

\[\begin{align*} k &\leftrightarrow 1/C\\ m &\leftrightarrow L\\ b &\leftrightarrow R\\ \end{align*}\]

Так як механічна система природним чином коливається з частотою ³\(\omega\approx\sqrt{k/m}\), то можна відразу вирішити електричний варіант за аналогією, надавши

\[\begin{equation*} \omega \approx \frac{1}{\sqrt{LC}} . \end{equation*}\]

Оскільки опір\(R\) аналогічно\(b\) в механічному корпусі, то виявляємо, що\(Q\) (коефіцієнт якості, а не заряду) резонансу обернено пропорційний\(R\), а ширина резонансу прямо пропорційна\(R\).

Приклад 22: Налаштування радіоприймача

Радіоприймач використовує такий тип схеми, щоб вибрати потрібну станцію. Оскільки приймач резонує на певній частоті, станції, частоти яких далекі, не будуть порушувати жодної реакції в ланцюзі. Значення\(R\) має бути досить малим, щоб тільки одна станція за раз була взята, але досить велика, щоб тюнер не був занадто образливим. Резонансну частоту можна налаштувати, регулюючи\(L\) або\(C\), але змінні конденсатори легше побудувати, ніж змінні індуктори.

Приклад 23: Числовий розрахунок

Телефонна компанія надсилає більше однієї розмови за один і той же провід, що досягається зміщенням кожного голосового сигналу в різний діапазон частот під час передачі. Кількість сигналів на провід можна максимізувати, зробивши кожен діапазон частот (відомий як смуга пропускання) якомога меншим. Виходить, що тільки відносно вузький діапазон частот необхідний для того, щоб зробити людський голос зрозумілим, тому телефонна компанія відфільтровує всі екстремальні максимуми і мінімуми. (Ось чому ваш телефонний голос відрізняється від вашого звичайного голосу.) \(\triangleright\)Якщо фільтр складається з ланцюга LRC з широким резонансом, зосередженим навколо 1,0 кГц, а конденсатор - 1\(\mu\text{F}\) (мікрофарад), яке значення індуктивності потрібно використовувати? \(\triangleright\)Вирішуючи для\(L\), ми маємо \[\begin{align*} L &= \frac{1}{ C\omega^2} \\ &= \frac{1}{(10^{-6}\ \text{F})(2\pi\times10^3\ \text{s}^{-1})^2} \\ &= 2.5\times10^{-3}\ \text{F}^{-1}\text{s}^2 \end{align*}\] Перевірка того, що це дійсно ті ж одиниці, що і Генрі, трохи втомлює, але вона будує характер: \[\begin{align*} \text{F}^{-1}\text{s}^2 &= (\text{C}^2/\text{J})^{-1}\text{s}^2 \\ &= \text{J}\cdot\text{C}^{-2}\text{s}^2 \\ &= \text{J}/\text{A}^2 \\ &= \text{H} \end{align*}\] Результат - 25 мГн (мілігені). Це насправді досить велике значення індуктивності, і вимагатиме великої, важкої, дорогої котушки. Насправді, є хитрість для того, щоб зробити цей вид схеми невеликою і дешевою. Існує своєрідний кремнієвий чіп, який називається операційним підсилювачем, який, крім усього іншого, може використовуватися для імітації поведінки індуктора. Основне обмеження операційного підсилювача полягає в тому, що він обмежений додатками з низьким енергоспоживанням.

10.5.3 Напруга і струм

Що фізично відбувається в одному з цих коливальних контурів? Давайте спочатку розглянемо механічний корпус, а потім проведемо аналогію зі схемою. Для простоти проігноруємо існування демпфування, тому в механічному генераторі немає тертя, а в електричному немає опору.

Припустимо, ми беремо механічний генератор і відтягуємо масу від рівноваги, потім відпускаємо її. Оскільки тертя має тенденцію протистояти силі пружини, ми можемо наївно очікувати, що нульове тертя дозволить масі миттєво стрибнути до положення рівноваги. Це не може статися, однак, тому що маса повинна мати нескінченну швидкість, щоб зробити такий миттєвий стрибок. Нескінченна швидкість вимагала б нескінченної кінетичної енергії, але єдиним видом енергії, доступною для перетворення в кінетичну, є енергія, що зберігається навесні, і це кінцева, а не нескінченна. На кожному кроці на шляху назад до рівноваги швидкість маси контролюється точно кількістю енергії пружини, яка до цих пір була перетворена в кінетичну енергію. Після того як маса досягає рівноваги, вона переростає за рахунок власного імпульсу. Він виконує однакові коливання по обидва боки рівноваги, і ніколи не втрачає амплітуду, оскільки тертя недоступне для перетворення механічної енергії в тепло.

Тепер з електричним генератором аналог положення заряджається. Відтягування маси від рівноваги схоже на відкладення зарядів\(+q\) і\(-q\) на обкладинках конденсатора. Оскільки опір має тенденцію чинити опір потоку заряду, ми можемо собі уявити, що без тертя, заряд миттєво протікає через індуктор (який, врешті-решт, є лише шматочком дроту), і конденсатор буде розряджатися миттєво. Однак такий миттєвий розряд неможливий, тому що він зажадав би нескінченного струму на одну мить. Нескінченний струм створив би нескінченні магнітні поля, що оточують індуктор, і ці поля мали б нескінченну енергію. Натомість швидкість потоку струму контролюється в кожну мить залежністю між кількістю енергії, що зберігається в магнітному полі, і кількістю струму, який повинен існувати для того, щоб мати таке сильне поле. Після того як конденсатор досягає\(q=0\), він переростає. Схема має свій вид електричної «інерції», тому що якби заряд припинив текти, через індуктор повинен був бути нульовий струм. Але струм в індукторі повинен бути пов'язаний з кількістю енергії, що зберігається в його магнітних полах. Коли конденсатор знаходиться на\(q=0\), вся енергія ланцюга знаходиться в індукторі, тому він повинен мати сильні магнітні поля навколо нього і досить багато струму, що проходить через нього.

Єдине, що може здатися моторошним тут, це те, що ми звикли говорити так, ніби струм в індукторі викликав магнітне поле, але тепер це звучить так, ніби поле викликає струм. Власне це симптоматика невловимого характеру причинно-наслідкового характеру у фізиці. В рівній мірі справедливо думати про причинно-наслідкові відносини в будь-якому випадку. Це може здатися незадовільним, однак, і, наприклад, насправді не потрапляє в питання про те, що призводить до різниці напруги на резисторі (в разі, коли опір кінцевий); має бути така різниця напруг, тому що без одного закон Ома передбачив би нульовий струм через резистор.

Тоді напруга - це те, чого насправді не вистачає в нашій історії досі.

Почнемо з вивчення напруги на конденсаторі. Напруга - це енергія електричного потенціалу на одиницю заряду, тому різниця напруг між двома обкладинками конденсатора пов'язана з величиною, на яку збільшилася б його енергія, якби ми збільшили абсолютні значення зарядів на обкладинках від\(q\) до\(q+dq\):

\[\begin{align*} V_C &= (U_{q+dq}-U_q)/dq \\ &= \frac{dU_C}{dq} \\ &= \frac{d}{dq}\left(\frac{1}{2C}q^2\right) \\ &= \frac{q}{C} \end{align*}\]

Багато книг використовують це як визначення ємності. Це рівняння, до\(C\) речі, напевно, пояснює історичну причину, чому\(C\) була визначена так, щоб енергія була обернено пропорційна заданому значенню\(C\): люди, які винайшли визначення, думали про конденсатор як про пристрій для зберігання заряду, а не енергії, а кількість заряду, що зберігається для фіксованого напруги (заряду «ємність») пропорційна\(C\).

л/індуктор вивільняє енергію і віддає її в чорний ящик.

Що стосується індуктора, ми знаємо, що якщо через нього протікає постійний постійний струм, то магнітне поле є постійним, а також кількість енергії, що зберігається; між індуктором та будь-яким іншим елементом ланцюга не обмінюється енергія. Але що робити, якщо струм змінюється? Магнітне поле пропорційно струму, тому зміна одного має на увазі зміну іншого. Для конкретності уявімо, що магнітне поле і струм обидва зменшуються. Енергія, що зберігається в магнітному полі, тому зменшується, і, зберігаючи енергію, ця енергія не може просто піти - якийсь інший елемент ланцюга повинен приймати енергію від індуктора. Найпростіший приклад, показаний на малюнку l, являє собою послідовну схему, що складається з індуктора плюс один інший елемент ланцюга. Не має значення, що це інший елемент ланцюга, тому ми просто називаємо його чорним ящиком, але якщо вам подобається, ми можемо думати про це як резистор, в цьому випадку енергія, втрачена індуктором, перетворюється на тепло резистором. Правило з'єднання говорить нам, що обидва елементи ланцюга мають однаковий струм через них, тому\(I\) може посилатися на будь-який з них, і так само правило петлі говорить нам\(V_{inductor}+V_{black\ box}=0\), тому два падіння напруги мають однакове абсолютне значення, яке ми можемо посилатися як\(V\). Яким би не був чорний ящик, швидкість, з якою він бере енергію від індуктора, задається\(|P|=|IV|\), так

\[\begin{align*} |IV| &= \left|\frac{dU_L}{dt}\right| \\ &= \left|\frac{d}{dt}\left( \frac{1}{2}LI^2\right) \right| \\ &= \left|LI\frac{dI}{dt}\right| ,\\ \text{or} |V| &= \left|L\frac{dI}{dt}\right| , \\ \end{align*}\]

який у багатьох книгах прийнято вважати визначенням індуктивності. Напрямок падіння напруги (знак плюс або мінус) таке, що індуктор чинить опір зміні струму.

Є одна дуже інтригуюча річ про цей результат. Припустимо, для конкретності, що чорний ящик на малюнку l - резистор, і що енергія індуктора зменшується, і перетворюється в тепло в резисторі. Падіння напруги на резисторі говорить про те, що на ньому є електричне поле, яке рухає струмом. Але звідки береться це електричне поле? Там немає ніяких звинувачень, які могли б створити його! Ми виявили один окремий випадок більш загального принципу, принципу індукції: мінливе магнітне поле створює електричне поле, яке є доповненням до будь-якого електричного поля, створеного зарядами. (Вірно і зворотне: будь-яке електричне поле, яке змінюється з часом, створює магнітне поле.) Індукція становить основу для таких технологій, як генератор і трансформатор, і в кінцевому підсумку вона призводить до існування світла, який представляє собою хвильовий малюнок в електричному і магнітному полах. Це все теми для глави 11, але справді чудово, що ми могли б прийти до такого висновку, ще не дізнавшись жодних подробиць про магнетизм.

m/Електричні поля, зроблені зарядами, 1, і шляхом зміни магнітних полів, 2 і 3.

Мультфільми на малюнку м порівнюють електричні поля, зроблені зарядами, 1, з електричними полями, зробленими зміною магнітних полів, 2-3. У м /1 двоє фізиків знаходяться в кімнаті, стеля якої заряджений позитивно і підлога якої негативно заряджений. Фізик на дні кидає позитивно заряджений куля для боулінгу в вигнуту трубу. Фізик вгорі використовує радіолокаційну гармату для вимірювання швидкості кулі, коли він виходить з труби. Вони виявляють, що м'яч сповільнився до того часу, коли він потрапляє на вершину. Вимірюючи зміну кінетичної енергії кулі, два фізики діють так само, як вольтметр. Вони роблять висновок, що верхня частина трубки знаходиться на більш високій напрузі, ніж нижня частина труби. Різниця в напрузі вказує на електричне поле, і це поле явно викликається зарядами в підлозі і стелі.

У м /2 ніде в номері не стягується жодних зборів, крім зарядженого м'яча для боулінгу. Рухомі заряди створюють магнітні поля, тому виникає магнітне поле, що оточує гвинтову трубу, поки куля рухається по ній. Магнітне поле було створено там, де раніше його не було, і це поле має енергію. Звідки могла з'явитися енергія? Він може надходити тільки від самого м'яча, тому м'яч повинен втрачати кінетичну енергію. Два фізика, які працюють разом, знову діють як вольтметр, і знову роблять висновок, що між верхньою і нижньою частиною труби існує різниця напруг. Це вказує на електричне поле, але це електричне поле не може бути створено жодними зарядами, тому що їх немає в приміщенні. Це електричне поле створювалося зміною магнітного поля.

Нижній фізик продовжує кидати кульки в трубу, поки труба не заповниться кульками, м/3, і, нарешті, встановиться стійкий струм. Поки труба наповнювалася кульками, енергія в магнітному полі неухильно зростала, і ця енергія викрадалася з кінетичної енергії куль. Але як тільки встановлений стійкий струм, енергія в магнітному полі більше не змінюється. Кулям більше не доведеться відмовлятися від енергії, щоб наростити поле, а фізик нагорі виявляє, що кулі знову виходять з труби на повній швидкості. Різниці напруги більше немає. Хоча є струм,\(dI/dt\) дорівнює нулю.

Приклад 24: Баласти

У газорозрядній трубці, такій як неонова вивіска, на трубку, наповнену газом, подається достатня напруга, щоб іонізувати деякі атоми в газі. Після створення іонів напруга прискорює їх, і вони вражають інші атоми, іонізуючи їх, а також і призводить до ланцюгової реакції. Це іскра, як затвор блискавки. Але як тільки іскра запускається, пристрій починає діяти так, ніби не має опору: все більше тече струм, без необхідності подавати більше напруги. Потужність\(P=IV\), росла б без обмежень, і трубка згоріла б сама. п/ Баласти для люмінесцентних світильників. Верх: великий, важкий індуктор використовується як баласт у старомодній люмінесцентній лампочці. Дно: невеликий твердотільний баласт, вбудований в основу сучасної компактної люмінесцентної лампи. Найпростішим рішенням є підключення індуктора, відомого як «баласт», послідовно з трубкою, і запустити все це на змінній напрузі. Під час кожного циклу, коли напруга досягає точки, де починається ланцюгова реакція, виникає сплеск струму, але індуктор чинить опір такій раптовій зміні струму, і енергія, яка в іншому випадку згоріла б лампочку, натомість направляється в будівництво магнітного поля. Звичайна побутова люмінесцентна лампочка складається з газорозрядної трубки, в якій скло покрито люмінесцентним матеріалом. Газ в трубці випромінює ультрафіолетове світло, яке поглинається покриттям, і покриття потім світиться у видимому спектрі. До недавнього часу баласт флюоресцентного світла був простим індуктором, а весь пристрій працював на частоті 60 Гц електричних ліній електропередач. Це призвело до того, що вогні дратівливо мерехтять на 120 Гц, а також могло викликати чутний гул, оскільки магнітне поле, що оточує індуктор, може чинити механічні сили на речі. У наші дні тенденція спрямована на використання твердотільної схеми, яка імітує поведінку індуктора, але на частоті в діапазоні кілогерц, усуваючи мерехтіння і гул. Сучасні компактні люмінесцентні лампи електронні мають баласти, вбудовані в їх підстави, тому їх можна використовувати як вставні заміни ламп розжарювання. Компактна люмінесцентна лампа використовує близько 1/4 електроенергії лампи розжарювання, служить в десять разів довше і економить 30 доларів електроенергії протягом свого терміну служби.

Обговорення Питання

◊ Що відбувається, коли фізик внизу на малюнку м /3 починає втомлюватися, і зменшується струм?

10.5.4 Розпад

До цих пір я м'яко педалював той факт, що, змінюючи характеристики генератора, можна виробляти неколивальну поведінку. Наприклад, уявіть, як взяти систему «маса на пружині» і зробити пружину слабшою і слабшою. У межі малого\(k\), це як би не було жодної пружини, а поведінка системи полягає в тому, що якщо ви штовхнете масу, вона просто починає сповільнюватися. Для тертя пропорційно\(v\), як ми припускали, результат полягає в тому, що швидкість наближається до нуля, але ніколи насправді не досягає нуля. Це нереально для механічного генератора, який не матиме зникаючого тертя при малих швидкостях, але цілком реально в разі електричного кола, для якого падіння напруги на резисторі дійсно наближається до нуля, оскільки струм наближається до нуля.

Нам навіть не доведеться зводити рівно\(k\) до нуля, щоб отримати неколивальну поведінку. Існує насправді кінцеве, критичне значення, нижче якого поведінка змінюється, так що маса ніколи навіть не робить його через один цикл. Це випадок овердемпфування, розглянутий на сторінці 186.

Електричні схеми можуть проявляти все ту ж поведінку. Для простоти розберемо тільки випадки ланцюгів LRC з\(L=0\) або\(C=0\).

RC ланцюг

o /RC ланцюг.

Спочатку аналізуємо RC ланцюг, o. Насправді доведеться «штовхати» ланцюг, наприклад, коротко вставивши батарею, щоб отримати будь-яку цікаву поведінку. Почнемо з закону Ома і рівняння напруги на конденсаторі:

\[\begin{align*} V_R &= IR \\ V_C &= q/C \end{align*}\]

Правило циклу говорить нам

\[\begin{equation*} V_R + V_C = 0 , \end{equation*}\]

і об'єднання трьох рівнянь призводить до співвідношення між\(q\) і\(I\):

\[\begin{equation*} I = -\frac{1}{RC}q \end{equation*}\]

Негативний знак говорить нам про те, що струм прагне знижувати заряд на конденсаторі, т. Е. Має сенс, що струм пропорційний\(q\): якщо\(q\) великий, то сили притягання між\(+q\) і\(-q\) зарядами на обкладинках конденсатора великі, і заряди будуть швидше протікати через резистор, щоб возз'єднатися. Якби на обкладинках конденсатора був нульовий заряд, причин для протікання струму не було б. Так як ампери, одиниця струму, такі ж, як кулони в секунду, виявляється, що кількість\(RC\) повинна мати одиниці секунд, і ви можете самі перевірити, що це правильно. \(RC\)тому називається постійною часу ланцюга.

Як саме робити\(I\) і\(q\) варіювати з часом? Рерайтинг\(I\) як\(dq/dt\), у нас

\[\begin{equation*} \frac{dq}{dt} = -\frac{1}{RC}q . \end{equation*}\]

Нам потрібна функція, похідна\(q(t)\) якої дорівнює самій собі, але помножена на негативну константу. Функція виду\(ae^t\), де\(e=2.718...\) знаходиться основа натуральних логарифмів, є єдиною, яка має свою похідну рівну собі, і\(ae^{bt}\) має свою похідну, рівну собі, помножену на\(b\). Таким чином, наше рішення

\[\begin{equation*} q = q_\text{o}\exp\left(-\frac{t}{RC}\right) . \end{equation*}\]

p/За проміжок часу\(RC\) заряд на конденсаторі зменшується в рази\(e\).

Ланцюг RL

q/RL ланцюг.

Схема RL, q, може бути атакована подібними методами, і це легко може бути показано, що вона дає

\[\begin{equation*} I = I_\text{o}\exp\left(-\frac{R}{L}t\right) . \end{equation*}\]

Константа часу RL дорівнює\(L/R\).

Приклад 25 Смерть від соленоїда; свічки запалювання

Коли ми раптом розірвемо ланцюг RL, що буде? Може здатися, що ми зіткнулися з парадоксом, оскільки у нас є лише дві форми енергії, магнітна енергія та тепло, і якщо струм раптово припиниться, магнітне поле має раптово зруйнуватися. Але куди дівається втрачена магнітна енергія? Він не може перейти в резистивний нагрів резистора, тому що ланцюг тепер був розірваний, і струм не може протікати! Вихід з цієї загадки полягає в тому, щоб визнати, що відкритий зазор в ланцюзі має опір, яке велике, але не нескінченне. Цей великий опір призводить до того, що\(L/ R\) постійна часу RL дуже мала. Струм, таким чином, продовжує протікати протягом дуже короткого часу, і протікає прямо через повітряний зазор, де ланцюг був розімкнутий. Іншими словами, іскра є! Ми можемо визначити, грунтуючись на декількох різних лініях міркувань, що падіння напруги з одного кінця іскри до іншого повинно бути дуже великим. По-перше, опір повітря велике, тому\(V= IR\) потрібно велика напруга. Ми також можемо міркувати, що вся енергія в магнітному полі розсіюється за короткий час, тому потужність, що розсіюється в іскрі, велика, і це вимагає великого значення\(V\).\(P= IV\) (\(I\)не великий - він зменшується від початкового значення.) І все ж третій спосіб досягти того ж результату - розглянути рівняння\(V_{L}=dI/dt\): оскільки постійна часу коротка, похідна за часом\(dI/dt\) велика. Саме так працюють свічки запалювання автомобіля. Інше застосування - до електробезпеки: раптово розірвати індуктивну ланцюг може бути небезпечно, тому що стільки енергії виділяється за короткий час. Також немає гарантії, що іскра буде розряджатися через повітряний проміжок; замість цього вона може пройти через ваше тіло, оскільки ваше тіло може мати менший опір.

Приклад 26: Радіопередавач іскрового проміжку

r/Приклад 26. На малюнку r показаний примітивний тип радіопередавача, званий передавачем іскрового проміжку, який використовується для відправки коду Морзе приблизно на рубежі двадцятого століття. Джерело високої напруги, V, зазвичай становить близько 10 000 вольт. Коли телеграфний вимикач, S, замкнутий, RC ланцюг зліва починає заряджатися. Зростаюча різниця напруг розвивається між електродами іскрового проміжку, Г. коли ця різниця напруг стає досить великою, електричне поле в повітрі між електродами викликає іскру, частково розряджаючи RC-ланцюг, але заряджаючи LC-ланцюг справа. Потім ланцюг LC коливається на своїй резонансній частоті (як правило, близько 1 МГц), але енергія цих коливань швидко випромінюється антеною, A, яка посилає радіохвилі (глава 11).

Питання для обговорення

◊ Суслик прогризає один з проводів в системі освітлення постійного струму у вашому передньому дворі, і світло вимикається. У той момент, коли ланцюг стає розімкнутою, ми можемо вважати оголені кінці дроту схожими на обкладинки конденсатора, з повітряним зазором (або зазором ховрах) між ними. Про яке значення ємності йдеться тут? Що б це розповіло вам про постійну\(RC\) часу?

10.5.5 Огляд комплексних чисел

s/Візуалізація комплексних чисел у вигляді точок на площині.

Для більш детального лікування складних чисел див. гл. 3 безкоштовної книги Джеймса Ніринга за адресою
http://www.physics.miami.edu/nearing/mathmethods/.

Припускаємо, що існує ряд\(i\), такий, що\(i^2=-1\). Квадратні коріння\(-1\) - то\(i\) і\(-i\). (В електротехнічних роботах, де\(i\) позначає струм, іноді\(j\) використовується замість нього.) Це породжує систему числення, яка називається комплексними числами, яка містить дійсні числа як підмножину. Будь-яке комплексне число\(z\) може бути записано у вигляді\(z=a+bi\), де\(a\) і\(b\) є\(b\) дійсними, а потім називаються дійсними і уявними частинами\(z\).\(a\) Число з нульовою дійсною частиною називається уявним числом. Комплексні числа можна візуалізувати як площину, причому дійсна числова лінія розміщена горизонтально, як\(x\) вісь знайомої\(x-y\) площини, а уявні числа йдуть уздовж\(y\) осі. Комплексні числа завершені таким чином, що дійсні числа не є: кожне ненульове комплексне число має два квадратних кореня. Наприклад, 1 є дійсним числом, тому воно також є членом комплексних чисел, а його квадратні\(-1\) корені - і 1. Так само\(-1\) має квадратні коріння\(i\) і\(-i\), і число\(i\) має квадратні коріння\(1/\sqrt{2}+i/\sqrt{2}\) і\(-1/\sqrt{2}-i/\sqrt{2}\).

Комплексні числа можна додавати і віднімати шляхом додавання або віднімання їх дійсних і уявних частин. Геометрично це те ж саме, що векторне додавання.

t/Додавання комплексних чисел подібно до додавання векторів, хоча дійсна і уявна осі насправді не відображають напрямки в просторі.

Комплексні числа\(a+bi\) і\(a-bi\), що лежать на рівних відстанях вище і нижче дійсної осі, називаються складними сполученнями. Результати квадратичної формули є або дійсними, або складними сполученнями один одного. Складний сполучений числа\(z\) позначається як\(\bar{z}\) або\(z^*\).

u/Комплексне число та його сполучений.

Комплексні числа підпорядковуються всім тим же правилам арифметики, що і реали, за винятком того, що їх неможливо впорядкувати уздовж одного рядка. Тобто сказати, чи більше одного комплексного числа іншого, не представляється можливим. Ми можемо порівняти їх з точки зору їх величин (їх відстані від походження), але два різних комплексних числа можуть мати однакову величину, тому, наприклад, ми не можемо сказати, чи\(1\) більше\(i\) або\(i\) більше\(1\).

Приклад 27: Квадратний корінь\(i\)

\ (i\) "> \(\triangleright\)Доведіть, що\(1/\sqrt{2}+i/\sqrt{2}\) це квадратний корінь\(i\). \(\triangleright\)Наш доказ може використовувати будь-які звичайні правила арифметики, крім замовлення. \[\begin{align*} (\frac{1}{\sqrt{2}}+\frac{i}{\sqrt{2}})^2 & = \frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}} +\frac{1}{\sqrt{2}}\cdot\frac{i}{\sqrt{2}} +\frac{i}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}} +\frac{i}{\sqrt{2}}\cdot\frac{i}{\sqrt{2}} \\ &= \frac{1}{2}(1+i+i-1) \\ &= i \end{align*}\] Приклад 27 показав один метод множення комплексних чисел. Однак є й інша приємна інтерпретація складного множення. Визначено аргумент комплексного числа як його кут у комплексній площині, виміряний проти годинникової стрілки від позитивної дійсної осі. Потім множення двох комплексних чисел відповідає множенню їх величин та додаванню їх аргументів. v/Комплексне число можна описати через його величину та аргумент. w/Аргумент\(uv\) - сума аргументів\(u\) і\(v\).

самоперевірка:

Використовуючи цю інтерпретацію множення, як можна знайти квадратні корені комплексного числа? (відповідь у зворотному боці PDF-версії книги)

Приклад 28: Ідентичність

Величина\(|z|\) комплексного числа\(z\) підпорядковується ідентичності\(|z|^2=z\bar{z}\). Щоб довести це, спочатку зауважимо, що\(\bar{z}\) має таку ж величину\(z\), як, оскільки перегортання її на іншу сторону реальної осі не змінює її відстані від початку. Множення\(z\) на\(\bar{z}\) дає результат, величина якого виявляється шляхом множення їх величин, тому величина\(z\bar{z}\) повинна бути рівною\(|z|^2\). Тепер нам залишається лише довести, що\(z\bar{z}\) це позитивне дійсне число. Але якщо, наприклад,\(z\) лежить проти годинникової стрілки від реальної осі, то\(\bar{z}\) лежить за годинниковою стрілкою від неї. Якщо\(z\) має позитивний аргумент, то\(\bar{z}\) має негативний, або навпаки. Таким чином, сума їх аргументів дорівнює нулю, тому результат має аргумент нуль, і знаходиться на позитивній дійсній осі. ^4 Вся ця система була побудована для того, щоб кожне число мало квадратне коріння. А як щодо кубових коренів, четвертих коренів тощо? Це стає ще більш дивним, коли ви хочете зробити це, а також? Ні. Складної системи числення, про яку ми вже говорили, достатньо для обробки всіх з них. Найприємніший спосіб мислення про нього - з точки зору коренів многочленів. У дійсній системі числення многочлен\(x^2-1\) має два корені, тобто два значення\(x\) (плюс і мінус один), які ми можемо підключити до многочлена і отримати нуль. Оскільки він має ці два справжніх кореня, ми можемо переписати многочлен як\((x-1)(x+1)\). Однак у многочлена\(x^2+1\) немає справжніх коренів. Негарно, що в реальній системі числення деякі поліноми другого порядку мають два корені і можуть бути враховані, а інші - ні. У комплексній системі числення всі вони можуть. Наприклад,\(x^2+1\) має коріння\(i\) і\(-i\), і може враховуватися як\((x-i)(x+i)\). Загалом, фундаментальна теорема алгебри стверджує, що в комплексній системі числення будь-який поліном n-го порядку може бути врахований повністю в\(n\) лінійні множники, а також можна сказати, що він має\(n\) складні корені, з розумінням того, що деякі корені можуть бути однаковими. Наприклад, многочлен четвертого порядку\(x^4+x^2\) може бути врахований як\((x-i)(x+i)(x-0)(x-0)\), і ми говоримо, що він має чотири корені,\(i\),\(-i\),, 0 і 0, два з яких трапляються однакові. Це розумний спосіб думати про це, тому що в реальному житті числа завжди є наближеннями в будь-якому випадку, і якщо ми зробимо крихітні, випадкові зміни в коефіцієнти цього многочлена, він матиме чотири різних кореня, з яких два просто трапляються дуже близькі до нуля.

Питання для обговорення

◊ Знайти\(\arg i\)\(\arg(-i)\), і\(\arg 37\), де\(\arg z\) позначає аргумент комплексного числа\(z\).

◊ Візуалізуйте наступні множення в комплексній площині, використовуючи інтерпретацію множення через множення величин і додавання аргументів:\((i)(i)=-1\),\((i)(-i)=1\),\((-i)(-i)=-1\).

◊ Якщо ми візуалізуємо\(z\) як точку в складній площині, як ми повинні візуалізувати\(-z\)? Що це означає з точки зору аргументів? Дайте подібні тлумачення для\(z^2\) і\(\sqrt{z}\).

◊ Знайти чотири різних комплексних числа\(z\) такі, що\(z^4=1\).

◊ Обчислити наступне. Використовуйте величину і аргумент, а не реальну і уявну частини.

\[\begin{equation*} |1+i| , \arg(1+i) , \left|\frac{1}{1+i}\right| , \arg\left(\frac{1}{1+i}\right) , \end{equation*}\]

Виходячи з наведених вище результатів, обчислити реальну і уявну частини\(1/(1+i)\).

10.5.6 Формула Ейлера

y/Леонард Ейлер (1707-1783).

Розширивши наш кругозір, включивши комплексні числа, природно, хочеться розширити функції, які ми знали і любили зі світу дійсних чисел, щоб вони також могли працювати над комплексними числами. Єдиний дійсно природний спосіб зробити це взагалі - використовувати серію Тейлора. Особливо красива річ відбувається з функціями\(e^x\)\(\sin x\), і\(\cos x\):

\[\begin{align*} e^x &= 1 + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + ... \\ \cos x &= 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - ... \\ \sin x &= x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - ... \end{align*}\]

Якщо\(x=i\phi\) є уявним числом, ми маємо

\[\begin{equation*} e^{i\phi} = \cos \phi + i \sin \phi , \end{equation*}\]

результат, відомий як формула Ейлера. Геометрична інтерпретація в комплексній площині показана на малюнку х.

x/Комплексне число\(e^{i\phi}\) лежить на одиничному колі.

Хоча спочатку результат може здатися чимось із виродкового шоу, застосування визначення експоненціальної функції дає зрозуміти, наскільки це природно:

\[\begin{align*} e^x = \lim_{n\rightarrow \infty} \left(1+\frac{x}{n}\right)^n . \end{align*}\]

Коли уявна,\(x=i\phi\) то величина\((1+i\phi/n)\) являє собою число, що лежить трохи вище 1 в комплексній площині. Для великих\(n\),\((1+i\phi/n)\) стає дуже близько до одиниці коло, і його аргументом є малий кут\(\phi/n\). Підвищення цього числа до n-ої степені множить його аргумент на\(n\), даючи число з аргументом of\(\phi\).

Формула Ейлера часто використовується у фізиці та техніці.

Приклад 29: Функції трига в терміні складних експоненціальних
\(\triangleright\)Запишіть функції синуса і косинуса через експоненціальні числа. \(\triangleright\)Формула Ейлера для\(x=-i\phi\) дає\(\cos \phi - i \sin \phi\), так як\(\cos(-\theta)=\cos\theta\), і\(\sin(-\theta)=-\sin\theta\). \[\begin{align*} \cos x &= \frac{e^{ix}+e^{-ix}}{2} \\ \sin x &= \frac{e^{ix}-e^{-ix}}{2i} \end{align*}\]

Приклад 30: Жорсткий інтеграл, зроблений легко

\(\triangleright\)Оцінити \[\begin{equation*} \int e^x \cos x dx \end{equation*}\] \(\triangleright\)Цей, здавалося б, неможливий інтеграл стає легким, якщо ми перепишемо косинус з точки зору експоненціальних: \[\begin{align*} \int e^x & \cos x dx \\ &= \int e^x \left(\frac{e^{ix}+e^{-ix}}{2}\right) dx \\ &= \frac{1}{2} \int (e^{(1+i)x}+e^{(1-i)x})dx \\ &= \frac{1}{2} \left( \frac{e^{(1+i)x}}{1+i}+\frac{e^{(1-i)x}}{1-i} \right)+ c \end{align*}\] Оскільки цей результат є інтегралом дійсної функції, ми хотіли б, щоб вона була реальною, і насправді це так, оскільки перший і другий члени є складними сполученнями один одного. Якби ми хотіли, ми могли б використовувати теорему Ейлера, щоб перетворити її назад в явно реальний результат. ^5

10.5.7 Імпеданс

Поки ми думали з точки зору вільних коливань ланцюга. Це схоже на механічний генератор, який ногами, але потім залишив коливатися самостійно без будь-якої зовнішньої сили, щоб вібрації не згасали. Припустимо, ланцюг LRC приводиться в дію з синусоїдально змінною напругою, наприклад, відбудеться, коли радіотюнер підключений до приймальної антени. Ми знаємо, що струм буде протікати в ланцюзі, і ми знаємо, що буде резонансна поведінка, але не обов'язково просто співвідносити струм з напругою в найбільш загальному випадку. Почнемо замість цього з особливих випадків ланцюгів LRC, що складаються тільки з опору, тільки ємності або тільки індуктивності. Нас цікавить лише сталий відповідь.

Чисто резистивний корпус легко. Закон Ома дає

\[\begin{equation*} I = \frac{V}{R} . \end{equation*}\]

У чисто ємнісному випадку відношення\(V=q/C\) дозволяє обчислити

\[\begin{align*} I &= \frac{dq}{dt} \\ &= C \frac{dV}{dt} . \end{align*}\]

Це частково аналогічно закону Ома. Наприклад, якщо подвоїти амплітуду синусоїдально змінної напруги змінного струму, похідна також\(dV/dt\) подвоїться, а амплітуда синусоїдально змінного струму також подвоїться. Однак це неправда\(I=V/R\), оскільки прийняття похідної синусоїдальної функції зміщує її фазу на 90 градусів. Якщо напруга змінюється як, наприклад\(V(t)=V_\text{o}\sin (\omega t)\), то струм буде\(I(t)=\omega C V_\text{o}\cos (\omega t)\). Амплітуда струму є\(\omega C V_\text{o}\), що пропорційно\(V_\text{o}\), але це не так, що\(I(t)=V(t)/R\) для якоїсь постійної\(R\).

z/В конденсаторі струм\(90°\) випереджає напругу по фазі.

Друга проблема, яка виникає, полягає в тому, що весь наш аналіз резистивних ланцюгів постійного струму був побудований на основі правила циклу та правила з'єднання, обидва з яких є твердженнями про суми. Щоб застосувати правило переходу до ланцюга змінного струму, наприклад, ми б сказали, що сума синусоїдальних хвиль, що описують струми, що надходять в перехід, дорівнює (в кожен момент часу) сумі синусоїдальних хвиль, що виходять назовні. Тепер синусоїдальні функції мають чудову властивість, яка полягає в тому, що якщо додати дві різні синусоїдальні функції, що мають однакову частоту, результат також є синусоїдою з цією частотою. Наприклад\(\cos\omega t+\sin\omega t=\sqrt{2}\sin(\omega t+\pi/4)\), що можна довести за допомогою trig тотожності. Однак тотожності трига можуть стати дуже громіздкими, і існує набагато простіша техніка, що включає складні числа.

aa/ Представлення функцій з точками в полярних координатах.

Рисунок аа показує корисний спосіб візуалізації того, що відбувається. Коли контур коливається з частотою\(\omega\), ми використовуємо точки в площині для представлення синусоїдальних функцій з різними фазами та амплітудами.

самоперевірка:

Яку з перерахованих нижче функцій можна представити таким чином? \(\cos(6t-4)\),\(\cos^2t\),\(\tan t\) (відповідь у зворотному боці PDF-версії книги)

Найпростіші приклади того, як це візуалізувати в полярних координатах\(\cos \omega t+\cos \omega t=2\cos \omega t\), - це такі, де все має однакову фазу, тому всі точки лежать уздовж однієї лінії в полярному графіку, і додавання - це так само, як додавання чисел на числовій лінії. Менш тривіальний приклад\(\cos\omega t+\sin\omega t=\sqrt{2}\sin(\omega t+\pi/4)\), можна візуалізувати, як на малюнку ab.

ab/Додавання двох синусоїдальних функцій.

Малюнок ab передбачає, що все це можна зв'язати між собою красиво, якщо ми ідентифікуємо нашу площину з площиною комплексних чисел. Наприклад, комплексні числа 1 і\(i\) представляють собою функції\(\sin\omega t\) і\(\cos\omega t\). Наприклад, на малюнку z напруга на конденсаторі - це синусоїда, помножена на число, яке дає його амплітуду, тому ми пов'язуємо цю функцію з числом, що\(\tilde{V}\) лежить на реальній осі. Його величина\(|\tilde{V}|\), дає амплітуду в одиницях вольт, в той час як його аргумент\(\arg \tilde{V}\), дає його фазовий кут, який дорівнює нулю. Струм кратний синусоїді, тому ми ототожнюємо його з числом,\(\tilde{I}\) що лежить на уявній осі. У нас\(\arg\tilde{I}=90°\), і\(|\tilde{I}|\) є амплітуда струму, в одиницях ампер. Але порівнюючи з нашим результатом вище, ми маємо\(|\tilde{I}|=\omega C|\tilde{V}|\). Об'єднавши інформацію про фазу і величину, ми маємо\(\tilde{I}=i\omega C\tilde{V}\). Це дуже схоже на закон Ома, тому ми пишемо

\[\begin{equation*} \tilde{I} = \frac{\tilde{V}}{Z_C} , \end{equation*}\]

де кількість

\[\begin{equation*} Z_C = -\frac{i}{\omega C} , \text{[impedance of a capacitor]} \end{equation*}\]

мають одиниці Ом, називається імпедансом конденсатора на цій частоті.

Має сенс, що імпеданс стає нескінченним при нульовій частоті. Нульова частота означає, що це займе нескінченний час, перш ніж напруга зміниться на будь-яку величину. Іншими словами, це схоже на ситуацію, коли конденсатор був підключений через клеми акумулятора і йому дозволено оселитися до стану, коли на обох клемах є постійний заряд. Оскільки електричні поля між пластинами постійні, енергії не додається або виводиться з поля. Конденсатор, який не може обмінюватися енергією з будь-яким іншим компонентом ланцюга, є не що інше, як розірвана (розімкнута) ланцюг.

Зверніть увагу, що ми маємо два типи комплексних чисел: ті, які представляють синусоїдальні функції часу, і ті, що представляють імпеданси. Ті, що представляють синусоїдальні функції, мають тильди зверху, які виглядають як маленькі синусоїдальні хвилі.

самоперевірка:

Чому конденсатор не може мати свій імпеданс, надрукований на ньому разом з його ємністю? (відповідь у зворотному боці PDF-версії книги)

Подібна математика (але цього разу з інтегралом замість похідної) дає

\[\begin{equation*} Z_L = i\omega L \text{[impedance of an inductor]} \end{equation*}\]

для індуктора. Має сенс, що індуктор має менший опір на більш низьких частотах, так як при нульовій частоті не відбувається зміни магнітного поля з плином часу. Жодна енергія не додається або не виділяється з магнітного поля, тому немає індукційних ефектів, і індуктор діє так само, як шматок дроту з незначним опором. Термін «дросель» для індуктора відноситься до його здатності «придушувати» високі частоти.

змінного струму/Струм через індуктор відстає від напруги на фазовий кут\(90°\).

Фазові відносини, показані на малюнках z і ac, можна запам'ятати за допомогою моєї власної мнемоніки «eVil», яка показує, що напруга (V) веде струм (I) в індуктивному ланцюзі, тоді як протилежне вірно в ємнісному. Більш традиційною мнемонікою є «ELI the ICE man», який використовує позначення Е для ЕРС, поняття, тісно пов'язане з напругою (див.

Підсумовуючи, імпеданси резисторів, конденсаторів та індукторів є

\[\begin{align*} Z_R &= R\\ Z_C &= -\frac{i}{\omega C}\\ Z_L &= i\omega L . \end{align*}\]

Приклад 31: Фільтри низьких і високих частот

Ланцюг LRC реагує лише на певний діапазон (смугу) частот, зосереджених навколо його резонансної частоти. Як фільтр, це відомий як смуговий фільтр. Якщо ви зменшите як баси, так і високі частоти на стерео, ви створили смуговий фільтр. Для створення фільтра високих частот або низьких частот нам потрібно лише послідовно вставити конденсатор або індуктор. Наприклад, дуже простий захист від перенапруги для комп'ютера може бути побудований, вставивши індуктор послідовно з комп'ютером. Бажана потужність 60 Гц від стіни є відносно низькою частотою, тоді як скачки напруги, які можуть пошкодити ваш комп'ютер, показують набагато більш швидкі зміни часу. Навіть якщо скачки напруги не є синусоїдальними сигналами, ми можемо якісно подумати про швидкий «сплеск» так, ніби він був дуже високою за частотою - як високочастотна синусоїдальна хвиля, вона дуже швидко змінюється. Індуктори, як правило, є великими, важкими, дорогими елементами схеми, тому простий захист від перенапруги, швидше за все, буде складатися з конденсатора паралельно з комп'ютером. (Насправді, як правило, просто підключіть одну сторону ланцюга живлення до землі через конденсатор.) Конденсатор має дуже високий імпеданс при низькій частоті потрібного сигналу 60 Гц, тому він відключає дуже мало струму. Але для високочастотного сигналу імпеданс конденсатора дуже малий, і він діє як нульовий імпеданс, легкий шлях, в який відводиться струм. Основні речі, з якими слід бути обережним з імпедансом, полягає в тому, що (1) концепція застосовується лише до ланцюга, який приводиться в дію синусоїдально, (2) імпеданс індуктора або конденсатора залежить від частоти.

Обговорення Питання

◊ На малюнку z на сторінці 607 показані напруга і струм для конденсатора. Намалюйте\(q\) -\(t\) графік, і використовуйте його, щоб дати фізичне пояснення фазової залежності між напругою і струмом. Наприклад, чому нульовий струм, коли напруга знаходиться на максимумі або мінімумі?

◊ Малюнок змінного струму на сторінці 609 показує напругу і струм для індуктора. Потужність вважається позитивною, коли енергія подається в магнітне поле індуктора. Намалюйте графік потужності, а потім графік, енергії\(U\), що зберігається в магнітному полі, і з його допомогою дати фізичне пояснення\(P\) -\(t\) графіка. Зокрема, обговоримо, чому частота подвоюється на\(P\) -\(t\) графіку.

◊ Зіставте особливості графіка на малюнку ac на сторінці 609 з історією, розказаною в мультфільмах на малюнку m /2-3 на стор. 598.

10.5.8 Потужність

Скільки потужності подається, коли коливальна напруга подається на імпеданс? \(P=IV\)Рівняння в цілому вірно, оскільки напруга визначається як енергія на одиницю заряду, а струм визначається як заряд за одиницю часу: множення їх дає енергію в одиницю часу. У ланцюзі постійного струму всі три величини були постійними, але в коливальному (змінному) ланцюзі всі три зміни часу відображення.

Резистор

Для початку розберемо корпус резистора. Наприклад, ви, мабуть, читаєте цю книгу з аркуша паперу, освітленого світиться лампочкою, яка рухається коливальною напругою з амплітудою\(V_\text{o}\). В особливому випадку резистора ми знаємо, що\(I\) і\(V\) знаходяться в фазі. Наприклад, якщо\(V\) змінюється як\(V_\text{o}\cos \omega t\), то\(I\) буде косинус, а також,\(I_\text{o}\cos \omega t\). Тоді потужність\(I_\text{o}V_\text{o}\cos^2\omega t\), яка завжди позитивна, ⁶ і варіюється в межах від 0 до\(I_\text{o}V_\text{o}\). Навіть якби зміна часу була\(\cos\omega t\) або\(\sin(\omega t+\pi/4)\), ми все одно мали б максимальну потужність\(I_\text{o}V_\text{o}\), тому що і напруга, і струм досягли б своїх максимумів одночасно. У лампочці момент максимальної потужності - це коли схема найбільш швидко нагріває нитку розжарювання. У той момент\(P=0\), коли через чверть циклу не протікає струм, і ніяка електрична енергія не перетворюється в тепло. Протягом усього циклу нитка позбавляється від енергії, випромінюючи світло. ⁷ Оскільки контур коливається на частоті ⁸ of\(60\ \text{Hz}\), температура насправді не встигає цикл вгору або вниз дуже сильно протягом періоду 1/60 с коливання, і ми не помічаємо жодних значних змін у яскравості світла , навіть з короткою експозицією фотографії.

оголошення/Потужність в резисторі: швидкість, з якою електрична енергія перетворюється в теплову.

Таким чином, ми дійсно хочемо знати середню потужність, «середня» означає середню за один повний цикл. Оскільки ми охоплюємо цілий цикл з нашим середнім, не має значення, яку фазу ми припускаємо. Давайте скористаємося косинусом. Загальна кількість енергії, переданої за один цикл, становить

\[\begin{align*} E &= \int dE \\ &= \int_0^T \frac{dE}{dt} dt , \\ \text{where $T=2\pi/\omega$ is the period.} E &= \int_0^T P dt \\ &= \int_0^T P dt \\ &= \int_0^T I_\text{o}V_\text{o} \cos^2\omega t dt \\ &= I_\text{o}V_\text{o} \int_0^T \cos^2\omega t dt \\ &= I_\text{o}V_\text{o} \int_0^T \frac{1}{2} \left(1+\cos 2\omega t\right) dt \\ \text{The reason for using the trig identity $\cos^2 x=(1+\cos 2 x)/2$ in the last step is that it lets us get the answer without doing a hard integral. Over the course of one full cycle, the quantity $\cos 2\omega t$ goes positive, negative, positive, and negative again, so the integral of it is zero. We then have} E &= I_\text{o}V_\text{o} \int_0^T \frac{1}{2} dt \\ &= \frac{I_\text{o}V_\text{o}T}{2} \end{align*}\]

Середня потужність становить

\[\begin{align*} P_{av} &= \frac{\text{energy transferred in one full cycle}}{\text{time for one full cycle}} \\ &= \frac{I_\text{o}V_\text{o}T/2}{T} \\ &= \frac{I_\text{o}V_\text{o}}{2} ,\\ \end{align*}\]

тобто середнє значення становить половину максимуму. Потужність варіюється від\(0\) до\(I_\text{o}V_\text{o}\), і вона витрачає рівну кількість часу вище і нижче максимуму, тому не дивно, що середня потужність знаходиться на півдорозі між нулем і максимумом. Підводячи підсумки, ми маємо

\[\begin{align*} P_{av} &= \frac{I_\text{o}V_\text{o}}{2} \text{[average power in a resistor]}\\ \end{align*}\]

для резистора.

Середньоквадратичні величини

Припустимо, одного разу електрична компанія вирішила почати подавати вашу електроенергію як постійний струм, а не змінним струмом. Як повинна бути пов'язана напруга постійного струму з амплітудою\(V_\text{o}\) змінної напруги, яку раніше використовували, якби вони хотіли, щоб ваші лампочки мали таку ж яскравість, як і раніше? Опір лампочки\(R\), є фіксованою величиною, тому нам потрібно співвіднести потужність з напругою і опором, усуваючи струм. У випадку з DC це дає\(P=IV=(V/R)V=V^2/R\). (Для постійного струму\(P\) і\(P_{av}\) однакові.) У корпусі змінного струму,\(P_{av} = I_\text{o}V_\text{o}/2=V_\text{o}^2/2R\). Оскільки в корпусі постійного струму немає коефіцієнта 1/2, таку ж потужність могла бути забезпечена постійною напругою, яка була меншою в рази\(1/\sqrt{2}\). Хоча ви почуєте, як люди кажуть, що побутова напруга в США становить 110 В, його амплітуда насправді\((110\ \text{V})\times\sqrt{2}\approx160\ \text{V}\). Причина позначення «напругою» полягає в\(V_\text{o}/\sqrt{2}\) тому, що люди, які наївно ставляться до ланцюгів змінного струму, можуть\(V_\text{o}/\sqrt{2}\) підключитися до звичного рівняння постійного струму, як\(P=V^2/R\) і отримати правильну середню відповідь. Величина\(V_\text{o}/\sqrt{2}\) називається «середньоквадратичним» напругою, що означає «середній квадрат кореня». Ідея полягає в тому, що якщо ви квадрат функції\(V(t)\), взяти її середнє (середнє) протягом одного циклу, а потім взяти квадратний корінь цього середнього, ви отримаєте\(V_\text{o}/\sqrt{2}\). Багато цифрові лічильники забезпечують середньоквадратичні показання для вимірювання змінних напруг і струмів.

Конденсатор

Для конденсатора розрахунок починається так само, але закінчується скручуванням. Якщо напруга змінюється як косинус\(V_\text{o}\cos \omega t\), то відношення\(I=CdV/dt\) говорить нам, що струм буде якоюсь постійною, помноженою на мінус синус,\(-V_\text{o}\sin \omega t\). Інтеграл, який ми зробили в разі резистора, тепер стає

\[\begin{equation*} E = \int_0^T -I_\text{o}V_\text{o} \sin \omega t \cos \omega t dt ,\\ \end{equation*}\]

і виходячи з цифри ae, ви можете легко переконати себе, що протягом одного повного циклу потужність витрачає дві чверті циклів, будучи негативними, а два - позитивними. Іншими словами, середня потужність дорівнює нулю!

ae/ Power в конденсаторі: швидкість, з якою енергія зберігається в (+) або видаляється з (-) електричного поля.

Чому це? Це має сенс, якщо думати з точки зору енергії. Резистор перетворює електричну енергію в тепло, ніколи не навпаки. Конденсатор, однак, просто зберігає електричну енергію в електричному полі, а потім віддає її назад. Для конденсатора,

\[\begin{align*} P_{av} &= 0 \text{[average power in a capacitor]}\\ \end{align*}\]

Зверніть увагу, що, хоча середня потужність дорівнює нулю, потужність в будь-який момент зазвичай не дорівнює нулю, як показано на малюнку ae. Конденсатор дійсно переносить енергію: просто запозичивши якусь енергію, він завжди окупає її в наступному квартальному циклі.

Індуктор

Аналіз для індуктора аналогічний тому, що для конденсатора: потужність, усереднена за один цикл, дорівнює нулю. Знову ж таки, ми просто тимчасово зберігаємо енергію в полі (на цей раз магнітне поле) і отримуємо її пізніше.

10.5.9 Відповідність імпедансу

af/Ми хочемо максимізувати потужність, що подається на навантаження\(Z_\text{o}\), регулюючи його імпеданс.

На малюнку аф показана часто зустрічається ситуація: ми бажаємо максимально збільшити середню потужність\(P_{av}\), що подається на навантаження за фіксовану величину\(V_\text{o}\), амплітуду коливального рушійного напруги. Ми припускаємо, що імпеданс лінії електропередачі,\(Z_T\) є фіксованою величиною, над якою ми не маємо контролю, але ми можемо проектувати навантаження, з будь-яким імпедансом\(Z_\text{o}\), який нам подобається. Наразі ми також припустимо, що обидва імпеданси резистивні. Наприклад,\(Z_T\) може бути опір довгого подовжувача, а\(Z_\text{o}\) може бути лампа на його кінці. Результат узагальнюється негайно, однак, до будь-якого виду імпедансу. Наприклад, навантаженням може бути магнітна котушка стереодинаміка, яка відображає як індуктивність, так і опір. (Для чисто індуктивного або ємнісного навантаження\(P_{av}\) дорівнює нулю, тому проблема не дуже цікава!)

Оскільки ми припускаємо, що і навантаження, і лінія електропередачі є резистивними, їх імпеданси додаються послідовно, а амплітуда струму задається

\[\begin{align*} I_\text{o} &= \frac{V_\text{o}}{Z_\text{o}+Z_T} ,\\ \text{so} P_{av} &= I_\text{o}V_\text{o}/2 \\ &= I_\text{o}^2Z_\text{o}/2 \\ &= \frac{V_\text{o}^2Z_\text{o}}{\left(Z_\text{o}+Z_T\right)^2}/2 . \text{The maximum of this expression occurs where the derivative is zero,} 0 &= \frac{1}{2}\frac{d}{dZ_\text{o}}\left[\frac{V_\text{o}^2Z_\text{o}}{\left(Z_\text{o}+Z_T\right)^2}\right] \\ 0 &= \frac{1}{2}\frac{d}{dZ_\text{o}}\left[\frac{Z_\text{o}}{\left(Z_\text{o}+Z_T\right)^2}\right] \\ 0 &= \left(Z_\text{o}+Z_T\right)^{-2}-2Z_\text{o}\left(Z_\text{o}+Z_T\right)^{-3} \\ 0 &= \left(Z_\text{o}+Z_T\right)-2Z_\text{o} \\ Z_\text{o} &= Z_T \end{align*}\]

Іншими словами, щоб максимізувати потужність, що подається на навантаження, ми повинні зробити імпеданс навантаження таким же, як і лінія електропередачі. Цей результат спочатку може здатися дивним, але це має сенс, якщо задуматися. Якщо імпеданс навантаження занадто високий, це як відкриття вимикача і розрив ланцюга; живлення не подається. З іншого боку, він не платить, щоб зробити імпеданс навантаження занадто малим. Роблячи його меншим, дає більше струму, але незалежно від того, наскільки малим ми його робимо, струм все одно буде обмежений імпедансом лінії електропередачі. Коли імпеданс навантаження наближається до нуля, струм наближається до цього фіксованого значення\(I_\text{o}^2Z_\text{o}\), а подавана потужність зменшується пропорційно\(Z_\text{o}\).

Максимізація передачі потужності шляхом узгодження\(Z_T\) з\(Z_\text{o}\) називається узгодженням імпедансу. Наприклад, 8-Омний домашній стереодинамік буде правильно підібраний до домашнього стереопідсилювача з внутрішнім опором 8 Ом, а автомобільні колонки 4 Ом будуть правильно підібрані до автомобільної стереосистеми з внутрішнім опором 4 Ом. Ви можете подумати, що відповідність імпедансу буде неважливим, тому що навіть якщо, наприклад, ми використовували автомобільну стереосистему для керування 8-омними динаміками, ми могли б компенсувати невідповідність, просто повернувши ручку гучності вище. Це дійсно один із способів компенсувати будь-яке невідповідність імпедансу, але завжди є ціна, яку потрібно заплатити. Коли імпеданси збігаються, половина потужності розсіюється в лінії електропередачі і половина в навантаженні. Однак, підключивши 4-омний підсилювач до 8-омного динаміка, ви б встановили ситуацію, коли два Вт розсіюються як тепло всередині підсилювача для кожного підсилювача, що доставляється до динаміка. Іншими словами, ви б витрачали енергію і, можливо, спалювали підсилювач, коли ви збільшили гучність, щоб компенсувати невідповідність.

10.5.10 Імпеданси послідовно і паралельно

Як імпеданси поєднуються послідовно і паралельно? Краса трактування їх як до складних чисел полягає в тому, що вони просто поєднуються за тими ж правилами, які ви вже дізналися як опори.

Приклад 32: Серійний імпеданс

\(\triangleright\)Конденсатор і індуктор послідовно один з одним приводяться в рух синусоїдально коливається напругою. На якій частоті струм максимізується? \(\triangleright\)Імпеданси послідовно, як і опори послідовно, додати. Конденсатор і індуктор діють так, ніби вони були єдиним елементом ланцюга з імпедансом. \[\begin{align*} Z &= Z_{L}+ Z_{C}\\ &= i\omega L-\frac{ i}{\omega C} .\\ \text{The current is then} \tilde{ I} = \frac{\tilde{ V}}{ i\omega L- i/\omega C} . \end{align*}\] Нас не хвилює фаза струму, тільки його амплітуда, яка представлена абсолютним значенням комплексного числа\(\tilde{ I}\), і це можна максимізувати, зробивши\(| i\omega L- i/\omega C|\) якомога менше. Але є деяка частота, при якій ця величина дорівнює нулю — \[\begin{gather*} 0 = i\omega L-\frac{ i}{\omega C}\\ \frac{1}{\omega C} = \omega L\\ \omega = \frac{1}{\sqrt{ LC}} \end{gather*}\] На цій частоті струм нескінченний! Що відбувається фізично? Це схема LRC с\(R=0\). Він має резонанс на цій частоті, і оскільки немає демпфування, реакція при резонансі нескінченна. Звичайно, будь-який реальний ланцюг LRC матиме деяке демпфування, однак невелике (див. Рисунок j на сторінці 181).

Приклад 33: Резонанс з демпфуванням

\(\triangleright\)Яка амплітуда струму в послідовному ланцюзі LRC? \(\triangleright\)Узагальнюючи з прикладу 32, додамо третій, реальний імпеданс: \[\begin{align*} |\tilde{ I}| &= \frac{|\tilde{ V}|}{| Z|} \\ &= \frac{|\tilde{ V}|}{| R+ i\omega L- i/\omega C|} \\ &= \frac{|\tilde{ V}|}{\sqrt{ R^2+(\omega L-1/\omega C)^2}} \end{align*}\] Цей результат зайняв би сторінки алгебри без техніки комплексного числа!

Приклад 34: Фільтр стерео кросовера другого порядку

Фільтр стерео кросовера гарантує, що високі частоти йдуть на твітер, а мінімуми - на НЧ-динамік. Це можна досягти, просто поставивши один конденсатор послідовно з твітером і один індуктор послідовно з НЧ-динаміком. Однак такий фільтр обрізається не дуже різко. Припустимо, ми моделюємо колонки як резистори. (Вони дійсно також мають індуктивність, оскільки в них є котушки, які служать електромагнітами для переміщення діафрагми, яка видає звук.) Тоді сила, яку вони малюють, є\(I^2 R\). Поклавши індуктор послідовно з НЧ-динаміком, аг/1, дає загальний опір, який на високих частотах переважає індуктор, тому струм пропорційний\(\omega^{-1}\), а потужність, отримана НЧ-динаміком, пропорційна\(\omega^{-2}\). Тег//Приклад 34. Фільтр другого порядку, як ag /2, - це той, який різкіше відключається: на високих частотах потужність йде як\(\omega^{-4}\). Щоб проаналізувати цю схему, спочатку обчислюємо загальний імпеданс: \[\begin{equation*} Z = Z_{L}+( Z_{C}^{-1}+ Z_R^{-1})^{-1} \end{equation*}\] Весь струм проходить через індуктор, тому якщо рушійна напруга подається зліва\(\tilde{ V}_d\), ми маємо \[\begin{equation*} \tilde{ V}_d = \tilde{ I}_{L} Z , \end{equation*}\] і ми також маємо \[\begin{equation*} \tilde{ V}_{L} = \tilde{ I}_{L} Z_L . \end{equation*}\] Правило петлі, нанесене на зовнішній периметр ланцюга, дає \[\begin{equation*} \tilde{ V}_{d} = \tilde{ V}_{L}+\tilde{ V}_R . \end{equation*}\] Пряма алгебра тепер призводить до \[\begin{equation*} \tilde{ V}_{R} = \frac{\tilde{ V}_{d}}{1+ Z_L/ Z_{C}+ Z_{L}/ Z_R} . \end{equation*}\] На високих частотах\(Z_{L}/ Z_C\) термін, який змінюється як\(\omega^2\), домінує, так\(\tilde{ V}_R\) і\(\tilde{ I}_R\) пропорційні\(\omega^{-2}\), а потужність пропорційна\(\omega^{-4}\).

Автори та атрибуція

Template:ContribCrowell