20.2.2: Кут контакту

Last updated
Save as PDF

Page ID: 76265

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Коли статична кількість рідини контактує з непроникною твердою поверхнею, вона, як правило, відпочиває так, що між поверхнею рідини та поверхнею твердої речовини існує характерний кут (вимірюється в рідині). Цей кут є кутом зіткнення, і відображається як кут\(\theta \) на малюнку XX.3. На малюнку XX.3 (а) зображений гострий кут зіткнення, при якому рідина трохи розтікається і «змочує» поверхню. На малюнку XX.3 (b) показаний тупий кут зіткнення, при якому рідина «згортається», а не змочує поверхню, скоріше, як краплі ртуті на більшості поверхонь, або краплі води на поверхні автомобіля, який був свіжовощений. У багатьох випадках кут контакту близький до будь-якого\( 0 ° \) або\( 180 ° \), хоча буде оцінено, що\( \theta \) якби був рівно нуль, рідина поширилася б

альт

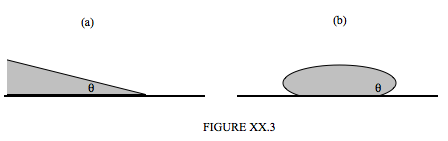
виходити в нескінченно тонкий шар, щоб покрити або «намочити» всю поверхню; а якби це було точно\( 180 ° \), то рідина, при відсутності інших сил (наприклад, її ваги!) , утворює сферичну кульку в контакті з поверхнею лише в одній точці. Кут зіткнення визначається характером обох поверхонь, і дуже чутливий до будь-яких поверхневих забруднень. Для того, щоб змочити поверхню, може знадобитися допомога води невеликою кількістю змочувача або миючого засобу; необхідна лише невелика кількість, тому що задіяна тільки поверхня, а не основна маса рідини. Хімічна природа зволожуючих речовин і миючих засобів виходить за рамки цих нот (тобто вона виходить за межі моєї сфери!) , Але як кут дотику залежить від поверхневого натягу дає корисний приклад техніки віртуальної роботи (див. Розділ 9.4 глави 9).

альт

Рисунок XX.4 представляє рідину, L, (наприклад, воду), що контактує з твердою речовиною, S, (наприклад, склом) та газом G (наприклад, повітрям). Кут контакту є\( \theta \), і поверхневі натяги (енергія на одиницю площі, або, для тих, хто розбирається в термодинаміці, вільна енергія Гіббса на одиницю площі) трьох інтерфейсів, як показано. Ми припустимо, що три носії поширюються\(l\) на відстань під прямим кутом до площини паперу (або екрану комп'ютера). Три фази знаходяться в рівновазі. Тепер, якщо ми перемістимо межу SLG вліво на відстань\( \delta x\), ми створимо нову область\( l \delta x \) інтерфейсу SL та нову область\( l \cos \theta \delta x \) інтерфейсу LG, при цьому втрачаємо область\( l \delta x \) інтерфейсу GS. Тому робота, виконана над системою\( \gamma_{SL} l \delta x + \gamma_{LG}l \cos \theta \delta x - \gamma_{GS} l \delta x \). За принципом віртуальної роботи це нуль, а значить

\[ \cos \theta = \dfrac{\gamma_{GS} - \gamma_{SL}}{\gamma_{LG}} . \tag{20.2.5}\label{eq:20.2.5} \]

Кут зіткнення гострий або тупий, залежно від\( \gamma_{GS} \) того, більше або менше\( \gamma_{SL} \).