20.3: Модуль зсуву та постійна кручення

Уявіть, що у нас є прямокутний блок з твердого матеріалу, як показано на лівій стороні малюнка XX.6. Тепер ми застосуємо пару дотичних сил$F$, як показано на правій стороні. (Я не вирішив йти всім балакучим і неформальним, сказавши «пару» сил; далеко від цього - я використовую слово «пара» в його формальному значенні в механіці.) Матеріал зазнає кутової деформації, а відношення тангенціальної сили на одиницю площі до отриманої кутової деформації називається модулем зсуву або модулем жорсткості. Його одиницею СІ є N m ⁻² рад ⁻¹, а розміри ML ⁻¹ T ⁻² θ ⁻¹. (Я б радив не використовувати «паскалі» на радіан. Одиниця «паскаль» найкраще обмежується тиском, який є нормальною силою на одиницю площі, і це не зовсім те ж саме, що тангенціальна сила на одиницю площі, про яку ми тут обговорюємо.) Слід переконати себе в тому, що у визначенні повинна бути вказана сила F, а не крутний момент, що надається парою. Якби блок був в два рази товщі, а сили були однаковими, ви б все одно отримали таку ж кутову деформацію.

Якщо ви тримаєте один кінець дроту або стрижня нерухомим і прикладіть крутний момент до іншого кінця, цей кінець буде скручуватися через кут, а відношення прикладеного крутного моменту до кута, через який дріт скручується$c$, є постійною кручення дроту. Побачити, як константа кручення залежить від модуля$\eta$ зсуву металу$a$ і радіуса і довжини$l$ дроту методом розмірів. Ви можете почати з припущення, що

$$c \propto \eta^\alpha a^\beta l^\gamma, \nonumber$$

але ви скоро опинитеся в скруті, тому що$a$ і$l$ є кожен з вимірів L. Однак у вас, ймовірно, не виникне труднощів з прийняттям припущення, що$\gamma = −1$ (чим довше дріт, тим легше його скручувати), і аналіз розмірів незабаром покаже, що$\alpha = 1$ і $\beta = 4$- що, будучи інтерпретацією, означає, що скрутити товсту дріт набагато складніше, ніж тонку дріт. Але чи можемо ми зробити краще і отримати вираз, крім простої пропорційності для константи кручення? Чи можемо ми знайти постійну пропорційності? Давайте спочатку спробуємо кілька простіших проблем і подивимося, як йдуть справи.

Розглянемо довгу тонку смужку або стрічку з металу. Під довгим і тонким я маю на увазі, що його довжина набагато більше його ширини, а ширина набагато більше його товщини. Я можу використовувати будь-який символ, який мені подобається, щоб представляти будь-яку кількість, яка мені подобається, так що я міг, якщо хотів, використовувати$\Xi$$m_\alpha$ для довжини,$G_2$ для ширини та товщини. Замість цього символи, які я виберу для представлення довжини, ширини та товщини смуги будуть, відповідно,$l, 2 \pi r$ і$\delta r$. Це здається дурним на даний момент, але врешті-решт ви будете раді, що я зробив цей вибір. Смужка показана в лівій частині малюнка XX.7.

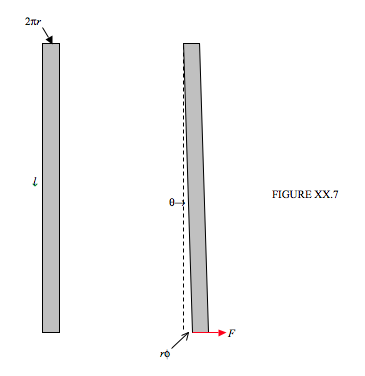
Тепер я збираюся закріпити верхній кінець смужки і застосувати силу$F$ до нижнього кінця, як показано на правій стороні малюнка XX.7, і я можу використовувати будь-який символ, який мені подобається, щоб представляти зміщення нижнього кінця, і я вибираю символ$r \phi$. Це означає, що кутове зміщення$\theta$$r \phi / l$ рівно.Тангенціальна сила на одиницю площі є$F/(2 \pi r \delta r)$, і тому

$$\eta = \frac{Fl}{2 \pi \phi r^2 \delta r} , \tag{20.3.1}\label{eq:20.3.1}$$

або

$$F = \frac{2 \pi \eta \phi r^2 \delta r}{l}. \tag{20.3.2}\label{eq:20.3.2}$$

Тепер я збираюся повернути смужці первісну форму, а потім я збираюся згорнути її в порожнисту циліндричну трубку, щоб вона тепер виглядала як металева трубочка для пиття. Окружність соломи є$2 \pi r$, її радіус -$r$ і товщина -$\delta r$ (рис. XX.8). (Тепер моє позначення починає мати певний сенс!)

Я буду тримати верхній кінець трубки фіксованим, і я буду застосовувати крутний момент$\tau = Fr$ до нижнього кінця. Трубка, очевидно, буде скручуватися через азимутальний кут,$\phi$ заданий

$$\tau = \frac{ 2 \pi \eta ^3 \delta r }{l} \phi . \tag{20.3.3}\label{eq:20.3.3}$$

Тому постійна кручення порожнистої трубки

$$c = \frac{2 \pi \eta r^3 \delta r }{l}. \tag{20.3.4}\label{eq:20.3.4}$$

Константа кручення довгого твердого циліндра (дроту) радіусом a є інтегралом цього від 0 до$a$, що дорівнює

$$c = \frac{\pi \eta a^4 }{2l} \tag{20.3.5}\label{eq:20.3.5}$$