4.10: Верх

Технічно ми класифікуємо тверді тіла як симетричні, асиметричні, сферичні та лінійні вершини відповідно до відносних розмірів їх основних моментів інерції. У цьому розділі, або принаймні в назві цього розділу, я маю на увазі «верх» в нетехнічному сенсі дитячої іграшки — тобто симетричне тіло, загострене на одному кінці, що обертається навколо своєї осі симетрії, із загостреним кінцем на землі або на столі. Технічно це «важка симетрична вершина з фіксованою однією точкою».

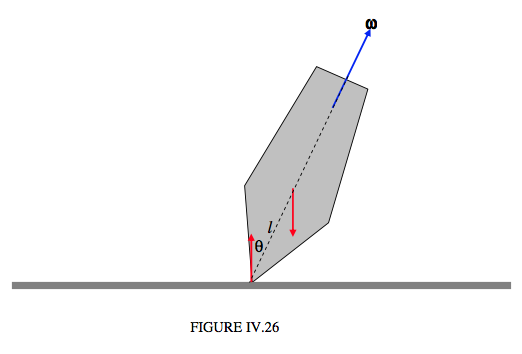
Я намалював це малюнок IV.26, обертаючись навколо своєї осі симетрії, яка робить кут\( \theta\) з вертикаллю. Відстань між центром маси і точкою зіткнення з таблицею становить l, вона має пару сил, що діють на нього — свою вагу і рівну, протилежну реакцію столу. На малюнку IV.27 я замінюю ці дві сили крутним моментом\( \boldsymbol\tau \), який має величину\( Mgl\sin\theta\).

Відзначимо, що, оскільки на систему діє зовнішній крутний момент, то вектор моменту моменту не фіксується.

Перш ніж брати участь у численних рівняннях, давайте витратимо трохи, якісно описуючи рух вершини, а також описуючи різні системи координат та кути, які ми будемо обговорювати. По-перше, ми будемо використовувати набір фіксованих пробілом координат. Ми\( O\) дозволимо початку координат бути в (фіксованому) точці, де кінчик верхньої торкається таблиці. Вісь\( Oz\) вказує вертикально вгору до зеніту. \( Oy\)Осі\( Ox\) і знаходяться в (горизонтальній) площині столу. Їх точна орієнтація не дуже важлива, але припустимо, що\( Ox\) точки через південь, а\( Oy\) точки через схід. \( Oxyz\)то являє собою набір для правші. Ми також будемо використовувати набір тіло-фіксованих осей, які я просто посилаюся на даний момент як 1, 2 і 3. 3-вісь - це вісь симетрії вершини. 1- і 2-осі перпендикулярні цьому. Їх точні положення не дуже важливі, але припустимо, що 31-площина проходить через невелику чорнильну крапку, яку ви позначили збоку зверху, і що система 123 являє собою набір для правші.

Ми збираємося описати орієнтацію вершини в якийсь момент за допомогою трьох кутів Ейлера\( \theta\),\( \phi\) і\( \psi\) (див. Рис. IV.28). Вісь симетрії вершини представлена важкою стрілкою, і вона перекидається під кутом\( \theta\) до\( z\) -осі. Я буду називати площину, нормальну до осі симетрії як «екватор» вершини, і вона нахилена\( \theta\) на\( xy\) -площині. Висхідний вузол екватора на\( xy\) -площині має азимут\( \phi\), і\( \psi\) являє собою кутову відстань 1-осі від вузла. Азимут осі симетрії вершини дорівнює\( \phi\) - 90 ° =\( \phi\) + 270°.

Тепер дозвольте трохи передбачити і описати рух верху, поки вона крутиться і піддається описаному вище моменту.

Вісь симетрії вершини збирається прецеса навколо\( z\) -осі, зі швидкістю, яка буде описана як\( \dot{\phi} \). За винятком деяких умов (які я врешті-решт опишу) цей прецесійний рух є світським. Це означає, що весь час\( \phi\) збільшується — він не коливається туди-сюди. Однак вісь симетрії не залишається під постійним кутом з\( z\) -віссю. Він коливається, або киває вгору і вниз між двома межами. Цей рух називається нутацією (лат.: nutare, кивати). Однією з наших цілей буде спробувати знайти швидкість нутації\( \dot{\phi} \) і знайти період і амплітуду нутації.

Це може виглядати так, ніби вершина обертається навколо своєї осі симетрії, але це не зовсім так. Якби вектор кутової швидкості був точно вздовж осі симетрії, він залишався б там, і не було б прецесії або нутації, і це не може бути, поки є крутний момент, що діє на вершині. Винятком було б, якби вершина крутилася вертикально (\( \theta\)= 0), коли на неї не діяло б крутного моменту. Верх може насправді це зробити, хіба що, якщо верхівка не крутиться досить швидко, така ситуація нестійка, і верх буде відхилятися від свого вертикального положення при найменшому обуренні. Однак при високих швидкостях обертання такий рух є стабільним, і дійсно однією з наших цілей має бути визначення найменшої кутової швидкості навколо осі симетрії такий рух є стабільним.

Однак, як уже згадувалося, якщо вершина не обертається вертикально, вектор\( \omega\) не спрямований вздовж осі симетрії. Ми будемо називати три компоненти\( \omega\) уздовж трьох тіло-фіксованих осей\( \omega_{1}\),\( \omega_{2}\) і\( \omega_{3}\), останній з них є складовою\( \omega\) уздовж осі симетрії. Одна з речей, яку ми виявимо, коли продовжимо аналіз, - це те, що\( \omega_{3}\) залишається постійним протягом усього руху. Також ви повинні вміти розрізняти\( \omega_{3}\) і\( \dot{\psi} \). Вони не однакові, через руху вузла. Насправді ви, напевно, це зрозумієте\( \psi = \omega_{3} - \dot{\phi} \cos \theta \). Дійсно, ми вже вивели співвідношення між складовою вектора кутової швидкості і швидкістю зміни кутів Ейлера — див. Рівняння 4.2.1, 2 і 3. Ми будемо використовувати ці відносини в наступному.

Щоб проаналізувати рух вершини, я збираюся використовувати Рівняння руху Лагранжа для консервативної системи. Якщо ви знайомі з рівняннями Лагранжа, це буде просто. Якщо ви цього не зробите, ви можете пропустити цей розділ, поки не ознайомитеся з механікою Лагранжа в главі 13. Однак я коротко ввів рівняння Лагранжа в розділі 4.4, в якому Рівняння руху Лагранжа було дано як

\[ \ \frac{d}{dt} \left(\frac{\partial T}{\partial \dot{q}_{j}}\right) - \left(\frac{\partial T}{\partial \dot{q}_{j}}\right) = P_{j}. \tag{4.10.1}\label{eq:4.10.1} \]

\(T\)Ось кінетична енергія системи. \(P_j\)- узагальнена сила, пов'язана з узагальненою координатою\(q_j\). Якщо сила є консервативною силою, то\(P_j\) може виражатися як негатив похідної потенційної енергетичної функції:

\[ \ P_{j} = - \left(\frac{\partial V}{\partial q_{j}}\right) \tag{4.10.2}\label{eq:4.10.2} \]

Таким чином, ми маємо рівняння руху Лагранжа для системи консервативних сил.

\[ \ \frac{d}{dt}\left(\frac{\partial V}{\partial \dot{q_{j}}}\right) - \frac{\partial V}{\partial q_{j}} = - \frac{\partial V}{\partial q_{j}} \tag{4.10.3}\label{eq:4.10.3} \]

Таким чином, при розв'язанні задачі в динаміці Лагранжа першим рядком нашого обчислення є запис виразу для кінетичної енергії. Починається перший рядок: «\( T = ...\)».

У цій задачі кінетична енергія

\[ \ T = \frac{1}{2} I_{1}(\omega^{2}_{1} + \omega^{2}_{2}) + \frac{1}{2} I_{3}\omega^{2}_{3} \tag{4.10.4}\label{eq:4.10.4} \]

Тут індекси відносяться до головних осей, 3 є віссю симетрії. Кути Ейлера\( \theta\) і\( \phi\) являють собою зенітну відстань і азимут відповідно осі симетрії по відношенню до лабораторних нерухомих (космічних нерухомих) осей. Кут Ейлера\( \psi\) вимірюється навколо осі симетрії. Складові кутової швидкості пов'язані зі швидкістю зміни кутів Ейлера за раніше виведеними формулами (Рівняння 4.2.1,2,3), тому\( \dot{\theta} , \dot{\phi} \) і\( \dot{\psi } \).

\[ \ T = \frac{1}{2} I_{1}(\dot{\theta}^{2} + \dot{\phi}^{2} \sin^{2} \theta) + \frac {1}{2} I_{3} (\dot{\psi} + \dot{\phi} \cos \theta)^{2} \tag{4.10.5}\label{eq:4.10.5} \]

Потенційна енергія

\[ \ V = Mgl\cos\theta + constant. \tag{4.10.6}\label{eq:4.10.6} \]

Записавши вирази для кінетичної та потенційної енергій з точки зору кутів Ейлера, ми тепер в змозі застосувати рівняння руху Лагранжа 4.10.3 для кожної з трьох координат. Почнемо з координати\( \phi\). Рівняння Лагранжа

\[ \ \frac{d}{dt}(\frac{\partial T}{\partial \dot{\phi}}) - \frac{\partial T}{\partial \phi} = -\frac{\partial V}{\partial \phi} \tag{4.10.7}\label{eq:4.10.7} \]

Ми бачимо, що\( \frac{\partial T}{\partial \phi} \) і\( \frac{\partial V}{\partial \phi} \) кожен нуль, так що\( \frac{d}{dt}\frac{\partial T}{\partial \phi} = 0, \) або\( \frac{\partial T}{\partial \phi} \) = постійна. Це має розміри моменту моменту, тому я буду називати постійну L ₁. При оцінці\( \frac{\partial T}{\partial \phi} \) похідної отримано для рівняння Лагранжа у\( \phi\):

\[ \ I_{1} \dot{\phi}sin^{2}\theta + I_{3} \dot{\phi}\cos^{2}\theta+ I_{3} \dot{\psi}\cos\theta = L_{1} \tag{4.10.8}\label{eq:4.10.8} \]

Залишу читача провести точно таку ж процедуру з координатою\( \psi\). Ви швидко зробите висновок, що\( \frac{\partial T}{\partial \psi} \) = постійна, яка має розміри кутового моменту, так називайте його\( L_{3}\), і тоді ви прийдете до наступного для рівняння Лагранжа в\( \psi\):

\[ \ I_{3}(\psi + \dot{\phi} \cos \theta) = L_{3} \tag{4.10.9}\label{eq:4.10.9} \]

Але вираз в дужках дорівнює\( \omega_{3}\) (див. Рівняння 4.2.3, хоча ми вже використовували його в Рівнянні\( \ref{eq:4.10.5}\)), тому отримуємо результат\( \omega_{3}\), що, складова кутової швидкості навколо осі симетрії, постійна під час руху вершини. Ймовірно, варто було б час читача в цей момент, щоб знову ретельно розрізнити в його свідомості різницю між\( \omega_{3}\) і\( \dot{\psi} \).

Виключити\( \dot{\psi} \) з рівнянь\( \ref{eq:4.10.8}\) і\( \ref{eq:4.10.9}\):

\[ \ \dot{\phi} = \frac{L_{1} - L_{3} cos \theta} {I_{1}\sin^{2}\theta} \tag{4.10.10}\label{eq:4.10.10} \]

Це рівняння говорить нам, як швидкість прецесії змінюється з\( \theta\) тим, як верхня киває або нутує вгору і вниз.

Ми також могли б виключити\( \dot{\phi} \) з рівнянь\( \ref{eq:4.10.8}\) і\( \ref{eq:4.10.9}\):

\[ \ \dot{\psi} = \frac{L_{3}}{I_{3}} - \frac{(L_{1}-L_{3} \cos\theta)\cos\theta}{I_{1}\sin^{2}\theta} \tag{4.10.11}\label{eq:4.10.11} \]

Рівняння\( \theta\) Лагранжа в трохи складніше, але ми можемо отримати третє Рівняння руху з сталості загальної енергії:

\[ \ \frac{1}{2} I_{1} (\dot{\theta}^{2} + \dot{\phi}^{2}\sin^{2}\theta) + \frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi}\cos\theta)^{2}+Mgl\cos\theta = E. \tag{4.10.12}\label{eq:4.10.12} \]

Ми можемо усунути\( \dot{\phi} \) і\( \dot{\psi} \) з цього, використовуючи Рівняння\( \ref{eq:4.10.10}\) і\( \ref{eq:4.10.11}\), щоб отримати рівняння в\( \theta\) і тільки час. Трохи провівши алгебру, отримуємо

\[ \ \dot{\theta}^{2} = A - B\cos\theta - \left(\frac{L_{1}-L_{3} \cos\theta}{I_{1} \sin\theta}\right)^{2}, \tag{4.10.13}\label{eq:4.10.13} \]

де

\[ \ A = \frac{1}{I_{1}}\left(2E - \frac{L^{2}_{3}}{I_{3}}\right) \tag{4.10.14}\label{eq:4.10.14} \]

і

\[ \ B = \frac{2Mgl}{I_{1}} \tag{4.10.15}\label{eq:4.10.15} \]

Поворотні точки в\( \theta\) -motion (тобто нутація) відбуваються там, де\( \dot{\theta} = 0\). Це результат (після деякої алгебри! — але досить просто (все одно) в кубічному рівнянні в\( c = \cos\theta\):

\[ \ a_{0} = a_{1}c + a_{2}c^{2} + Bc^{3} = 0 \tag{4.10.16}\label{eq:4.10.16} \]

де

\[ \ a_{0} = A - \left(\frac{L_{1}}{I_{1}}\right)^{2} = \frac{2E}{I_{1}} - \frac{L_{3}^{2}}{I_{1}I_{3}}- \frac{L_{1}^{2}}{I_{1}^{2}}, \tag{4.10.17}\label{eq:4.10.17} \]

\[ \ a_{1} = \frac{2L_{1}L_{3}}{I^{2}_{1}} - B = \frac{2L_{1}L_{3}}{I^{2}_{1}} - \frac{2Mgl}{I_{1}} \tag{4.10.18}\label{eq:4.10.18} \]

і

\[ \ a_{2} = -A - \left(\frac{L_{3}}{I_{1}}\right)^{2} = -\left[\frac{2E}{I_{1}} - \frac{L^{2}_{3}}{I_{1}I_{3}}- \left(\frac{L_{3}}{I_{1}}\right)^{2}\right] \tag{4.10.19}\label{eq:4.10.19} \]

Тепер рівняння\( \ref{eq:4.10.16}\) є кубічним рівнянням в\( \cos \theta\) і воно має або один реальний корінь, або три реальних кореня, і в останньому випадку два з них або всі три можуть бути рівними. Ми також повинні мати на увазі, що\( \theta\) є реальним, лише якщо\( \cos \theta\) він знаходиться в діапазоні від −1 до+1. Ми намагаємося знайти межі нутації, тому сподіваємося, що знайдемо два і тільки два реальних значення\( \theta\). (Якщо верхівка вершини була розташована на вершині точки - наприклад, якби вона була розташована на вершині Ейфелевої вежі, а не на горизонтальному столі - ви могли б\( \theta\) мати> 90 °.)

Щоб спробувати зрозуміти це краще, я сконструював у своїй свідомості топ, дещо схожий за формою на той, що зображений на малюнках IV.25 і 26, діаметром близько 4 см, висотою 7 см, з латуні. Для конкретної форми та розмірів, які я собі уявляв, це спрацювало, щоб мати наступні параметри, округлені до двох значущих фігур:

М = 0,53 кг л = 0,044 м I ₁ = 1,7×10 ⁻⁴ кг м ² I ₃ = 9,8×10 ⁻⁵ кг м ²

Я думав, що я б спина зверху так, що\( \omega_{3}\) (який, як ми бачили, залишається постійним протягом усього руху) 250 рад с ^-1, і я б почати верхню (\( \dot{\phi} = \dot{\theta} = 0 \)) при\( \theta\) = 30 °. А потім відпустити. Імовірно, він негайно почне падати, і 30 ° тоді буде верхньою межею нутації. Ми хочемо побачити, як далеко він впаде, перш ніж знову кивати вгору. З\( \omega_{3}\) = 250 рад s ⁻¹ ми знаходимо, з Рівняння,\( \ref{eq:4.10.9}\) що

\( L_{3}\)= 2,45 х 10 ^-2 Дж

Крім того, я припускаю, що\( \dot{\phi} \) = 0 коли\( \theta\) = 30 °, і Рівняння\( \ref{eq:4.10.10}\) говорить нам, що

Л ₁ = 2,121762 х 10 ^{-2 Жс}

Тоді з g = 9.8 m s ⁻², ми маємо, з Рівняння\( \ref{eq:4.10.15}\),

Б = 2,688659 х 10 ³ с ^-2.

Мої початкові умови, що\( \dot{\phi} \) і\( \dot{\theta} \) кожен нуль, коли\( \theta\) = 30 °, і Рівняння\( \ref{eq:4.10.10}\) і\( \ref{eq:4.10.13}\) між ними говорять нам, що\( A = B \cos\) 30 °, так що

А = 2,328447 х 10 ³ с ^-2.

З рівнянь 4.12.17, 18 і 19 ми тепер маємо

а ₀ = -1,324989 х 10 ³ с ^-2

а1= +3,328586 х 10 ³ с ^-2

а2= -2,309834 х 10 ³ с ^-2

і у нас вже є

Б = 2,688659 х 10 ³ с ^-2.

«Правило знаків» для рівнянь поліномів, якщо ви знайомі з ним, говорить нам, що немає негативних дійсних коренів (тобто немає розв'язків\( \theta\) з> 90 °), і справді, якщо ми вирішимо кубічне рівняння,\( \ref{eq:4.10.16}\) ми отримаємо

с = 0.824596, 0.866025, 6.9000406

Другий з них відповідає\( \theta\) = 30 °, який ми вже знали, повинен бути рішенням. Дійсно, ми могли б розділити Рівняння\( \ref{eq:4.10.16}\) на\( c – \cos\) 30 °, щоб отримати квадратне рівняння для решти двох коренів, але, мабуть, найкраще вирішити кубічне рівняння таким, яким воно є, щоб переконатися, що\( \cos\) 30 ° дійсно є рішенням, тим самим забезпечуючи перевірку на арифметичні. Третє рішення не дає нам реального\( \theta\) (ми швидше сподівалися, що це станеться). Друге рішення - нижня межа нутації, відповідна\( \theta\) = 34 ° 27'.

Як правило, однак, верхня частина буде нутувати між двома значеннями\( \theta\). Назвемо ці два значення\( \alpha\) і\( \beta\),\( \alpha\) будучи меншим (більш вертикальним) з двох. Я буду\( \theta = \alpha\) називати «верхню межу» руху, хоча\( \alpha<\beta\), оскільки це відповідає більш вертикальному положенню верхньої частини. Ми трохи подивилися на рух в\( \theta\); тепер давайте подивимося на рух в\( \phi\), починаючи з Рівняння\( \ref{eq:4.10.10}\):

\[ \ \dot{\phi}= \frac{L_{1}-L_{3}\cos \theta}{I_{1}\sin^{2}\theta} \tag{4.10.10.}\label{eq:4.10.10.} \]

Якщо початкові умови такі, що\( L_{1}>L_{3}\cos\alpha\) (і тому завжди більше\( L_{3}\cos\theta\))\( \hat{\phi} \) завжди позитивний. Рух тоді щось на зразок я намагаюся проілюструвати на малюнку IV.29

Цей рух відповідає початковій умові, в якій ви даєте верхній початковий поштовх у напрямку вперед, як зазначено маленькою синьою стрілкою. Якщо початкові умови такі\( \cos\alpha>\frac{L_{1}}{L_{3}}>\cos\beta\), що, ознака\( \dot{\phi} \) відрізняється у верхній і нижній межах. Так проілюстровано на малюнку IV.30

Цей рух виникне, якби ви спочатку дали невеликий поштовх назад, перш ніж відпустити вершину, як вказує маленька синя стрілка.

Якщо початкові умови такі\( L_{1}=L_{3}\cos\alpha\), що, то\( \dot{\theta} \) і\( \dot{\phi} \) кожен нуль у верхній межі нутації, і така була ситуація в нашому числовому прикладі. Це відповідає просто відпускати верхню краплю, коли ви відпускаєте її, не даючи йому ні вперед, ні назад. Це проілюстровано на малюнку IV.31.

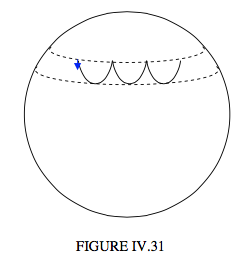
Як ми виявили, роблячи наш числовий приклад, початкові умови,\( \dot{\theta} = \dot{\phi} = 0 \) коли\( \theta = \alpha\) призводять, у цьому третьому типі руху, до

\[ \ L_{1} = L_{3} \cos \alpha \tag{4.10.20}\label{eq:4.10.20} \]

і

\[ \ A = B \cos \alpha \tag{4.10.21}\label{eq:4.10.21} \]

У випадку Рівняння\( \ref{eq:4.10.13}\) стає

\[ \ \dot{\theta}^{2} = B(\cos \alpha - \cos \theta) - [\frac{L_{3}(\cos \alpha - \cos \theta)}{I_{1}\sin\theta}]^{2} \tag{4.10.22}\label{eq:4.10.22} \]

Нижня межа нутації (тобто як далеко падає вершина) знаходить, поставивши\( \theta = \beta\) при\( \dot{\theta} \) = 0. Це дає наступне квадратне рівняння для\( \beta\):

\[ \cos^{2}\beta - \frac{L^{2}_{3}}{I^{2}_{1} B} \cos\beta + \frac{L^{2}_{3}\cos \alpha}{I_{1} \sin \theta} \tag{4.10.23}\label{eq:4.10.23} \]

У нашому числовому прикладі це

\[ \cos^{2}\beta -7.725002 \cos \beta +5.690048 = 0, \tag{4.10.24}\label{eq:4.10.24} \]

який, природно, має ті ж два рішення, які ми отримали при вирішенні кубічного рівняння, а саме 0.824 596 і 6.900 406.

Згадуючи визначення B (Equation\( \ref{eq:4.10.15}\)), ми бачимо, що Рівняння\( \ref{eq:4.10.23}\) можна записати

\[ \ \cos \alpha - \cos\beta = \frac{2MglI_{1}}{L_{3}^{2}}\sin^{2}\beta, \tag{4.10.25}\label{eq:4.10.25} \]

з якого ми бачимо, що чим більше\( L_{3}\), тим менше різниця між\( \alpha\) і\( \beta\) - тобто тим менше амплітуда нутації.

Рівняння\( \ref{eq:4.10.12}\), за допомогою Рівняння\( \ref{eq:4.10.10}\) і\( \ref{eq:4.10.11}\), можна записати:

\[ \ E - \frac{L^{2}_{3}}{2I_{3}}-\frac{1}{2}I_{1}\dot{\theta}^{2} = \frac{1}{2I_{1}}(L_{1}\csc\theta -L_{3} \cot \theta )^{2} + Mglcos\theta . \tag{4.10.26}\label{eq:4.10.26} \]

Ліва сторона - сумарна енергія мінус спінові і нутаційні кінетичні енергії. Таким чином, права сторона являє собою ефективну потенційну енергію, яку\( V_{e}(\theta)\) називають еталонною рамкою, яка обертається разом з прецесією. Термін не\( Mgl\sin\theta\) потребує пояснень. Негативним від похідної першого члена з правого боку буде «фіктивна» сила, яка «існує» у співобертаючій системі відліку. Ефективна\( V_{e}(\theta)\) потенційна енергія дається

\[ \ \frac{V_{e}(\theta)}{L_{1}^{2}/(2I_{1})}=[\csc\theta- (L_{3}/L_{1})\cot\theta]^{2} + \frac{2I_{1}Mgl\cos\theta}{L_{1}^{2}}. \tag{4.10.27}\label{eq:4.10.27} \]

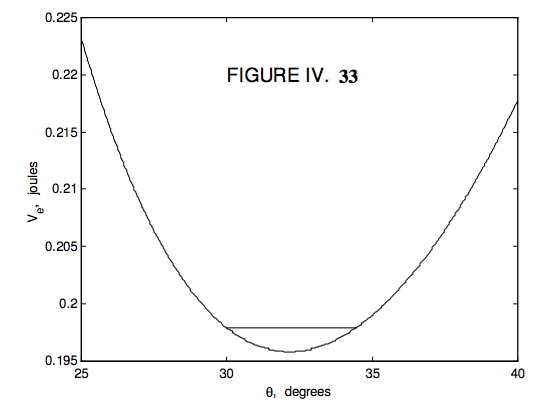
Я малюю на\( V_{e}(\theta)\) рисунках IV.32 і 33, використовуючи значення, які ми використовували в нашому числовому прикладі - тобто:

\[ \ V_{e}(\theta) = 1.32081(\csc\theta - 1.154701\cot\theta)^{2} +0.229536\cos\theta \qquad \text{joules}. \tag{4.10.28}\label{eq:4.10.28} \]

Малюнок 32 нанесений до 90 ° (хоча, як говорилося раніше, можна було б піти далі цього, якби верхівка не крутилася на горизонтальному столі), а на малюнку 33 близький погляд 2 до мінімального. Можна побачити, що якщо\( E - L_{3}^{3}/(2I_{2}) = 0.1979 \) ефективна потенційна енергія (яка не може йти вище цієї, і досягає цього значення лише тоді, коли)\( \dot{\theta} \) = 0, межі нутації знаходяться в межах від 30 ° до 34° 24 '. Для даного\( L_{3}\), для більшої загальної енергії межі нутації відповідно ширші. Але для даної сумарної енергії, чим більше\( L_{3}\) складова моменту моменту моменту, тим нижче буде горизонтальна лінія і тим вужче межі нутації. Якщо верх втрачає енергію (наприклад, через опір повітря або тертя в місці контакту з таблицею), постійна лінія E = стане нижчою 2 і нижче, а амплітуда нутації буде ставати все менше і менше. Якщо\( E - L_{3}^{2}/(2I_{3}) \) дорівнює мінімальному значенню\( V_{e}(\theta)\) є тільки одне рішення для\( \theta\), а нутації немає. Для енергії менше цього, немає стаціонарного значення\( \theta\) і верх опускається.

Ми можемо знайти швидкість справжньої регулярної прецесії досить просто так - і це часто робиться у вступних книгах.

На малюнку IV.34 вектор\( \bf{L}\) представляє кутовий момент в якийсь час, а через часовий проміжок\( \delta t\) пізніше зміна кутового моменту є\( \boldsymbol\delta { \bf L}\). Кутовий імпульс змінюється через зовнішнього крутного моменту, який є горизонтальним вектором величини\( Mgl\sin\theta\) (нагадайте про себе з рис. XV .26 і 27). Швидкість зміни моменту моменту задається по\( \bf{L} = \tau \). З часом\( \delta t\) кінчик вектора\( \bf{L}\) переміщається через «відстань»\( \tau \delta t\). Позначимо\( \boldsymbol\Omega\) прецесійної кутовою швидкістю (величину якої ми досі називали\( \dot{\phi}\)). Кінчик вектора кутового моменту рухається в малому колі радіуса\( L\sin \theta\). Тому ми це бачимо\( \tau = \Omega L \sin\theta\). Далі,\( \tau \) перпендикулярно обох\( \boldsymbol\Omega\) і\( \bf{L}\). Тому в векторних позначеннях

\[ \boldsymbol\tau = \boldsymbol\Omega \times { \bf L} \tag{4.10.29}\label{eq:4.10.29} \]

Зверніть увагу, що величина\( \boldsymbol\tau \) є\( Mgl\sin\theta\) і величина\( \boldsymbol\Omega \times \bf{L}\) є\( \Omega L \sin\theta\), так що швидкість прецесії

\[ \ \Omega = \frac{Mgl}{L} \tag{4.10.30}\label{eq:4.10.30} \]

і є незалежним від\( \theta\).
Можна продовжувати аналізувати рух вершини майже нескінченно довго, але є два особливих випадки, які, мабуть, варто відзначити і які я опишу.

Особливий випадок I\(L_{1} = L_{3}\).
У цьому випадку рівняння\( \ref{eq:4.10.27}\) стає

\[ \ \frac{V_{e}(\theta)}{Mgl}= C(csc\theta - cot\theta)^{2} +\cos\theta \tag{4.10.31}\label{eq:4.10.31} \]

де

\[ \ C = \frac{L_{1}^{2}}{2MglI_{1}} \tag{4.10.32}\label{eq:4.10.32} \]

Це може бути досить малоймовірним, що\(L_{1} = L_{3}\) саме, але цей випадок представляє інтерес частково тому, що він є винятковим в тому, що\( V_{e}(0)\) не йде до нескінченності; насправді\( V_{e}(0)=Mgl\) незалежно від значення\( C\). Спробуйте замінити\( \theta\) = 0 в Рівняння\( \ref{eq:4.10.31}\) і подивіться, що ви отримаєте! Права сторона дійсно 1, але вам, можливо, доведеться трохи попрацювати, щоб дістатися туди. Інша причина, чому цей випадок представляє інтерес, полягає в тому, що він робить корисний вступ до справи II, що не є неможливим, а саме\( L_{1}\) це приблизно дорівнює\( L_{3}\), що призводить до руху певного інтересу.

На малюнку IV.35 я\( \frac{V_{e}(0)}{Mgl}\) малюю кілька різних\( C\).

З графіків виглядає так, ніби\( C \geq 2\), є одне положення рівноваги, воно знаходиться при\( \theta\) = 0 ° (тобто вершина вертикальна), а рівновага стабільна, якщо\( C < 2\), є два положення рівноваги: вертикальне положення нестабільне, а інше положення рівноваги - стабільний. Таким чином, якщо верх обертається швидко (великий\( C\)), він може обертатися тільки у вертикальному положенні («сплячий верх»), але, оскільки верх сповільнюється внаслідок тертя і опору повітря, вертикальне положення стане нестійким, а верх буде падати до позитивного значення\( \theta\).

Ці відрахування правильні, для\( \frac{dV_{e}}{d \theta} = 0\) результатів

\[ \ 2C(1-cos\theta)^{2} = \sin^{4}\theta \tag{4.10.33}\label{eq:4.10.33} \]

Одне рішення є\( \theta = 0\), а друга диференціація покаже, що це стабільно або\( C\) нестабільно відповідно до того, чи більше або менше 2, хоча друга диференціація трохи втомлює, і її можна уникнути. Ми також можемо відзначити, що\( 1 − \cos\theta\) це загальний коефіцієнт двох сторін рівняння\( \ref{eq:4.10.33}\), і його можна розділити, щоб отримати кубічне рівняння в\( \cos\theta\):

\[ \ 2C-1-(2C+1)\cos\theta -\cos^{2}\theta - \cos^{3}\theta =0, \tag{4.10.34}\label{eq:4.10.34} \]

який можна було б вирішити, щоб знайти другу точку рівноваги - але це знову трохи втомлює. Менш виснажливим способом може бути взяти квадратний корінь кожної сторони рівняння\( \ref{eq:4.10.33}\):

\[ \ \sqrt{2C}(1-\cos\theta)=1-\cos^{2}\theta \tag{4.10.35}\label{eq:4.10.35} \]

а потім розділити на загальний коефіцієнт (1 −\ cos θ) для отримання

\[ \cos \theta = \sqrt{2C} - 1, \tag{4.10.36}\label{eq:4.10.36} \]

який дає реальний\( \theta\) тільки якщо\( C \geq 2\). Зверніть увагу також, якщо\(C = \frac{1}{2} \),\( \theta\) = 90 °.

Особливий випадок II. \( L_{3} \approx L_{1}\).

Іншими словами,\( L_{1}\) і\( L_{3}\) не сильно відрізняються. На малюнку IX.36\( \frac{V_{e}(0)}{Mgl}\) малюю кілька різних\( C\), для\( L_{3} = 1.01 L_{1}\).

Ми бачимо, що для досить великого діапазону\( C\) більше 2 стабільне положення рівноваги близьке до вертикального. Незважаючи на те, що крива для\( C = 2\) має дуже широкий мінімум, фактичний мінімум трохи менше 17 °. (Я не опрацьовував точну позицію — я залишу це читачеві.)