Skip to main content
LibreTexts - Ukrayinska

2.2: Значення обертальної інерції

  1. Last updated
  2. Save as PDF
  • Page ID
    76154

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Якщо сила діє на тіло, тіло прискорюється. Ставлення прикладеної сили до отриманого прискорення - це інерція (або маса) тіла.

    Якщо крутний момент діє на тіло, яке може вільно обертатися навколо якоїсь осі, тіло зазнає кутового прискорення. Ставлення прикладеного крутного моменту до отриманого кутового прискорення - обертальна інерція тіла. Це залежить не тільки від маси тіла, але і від того, як ця маса розподілена по відношенню до осі.

    Розглянемо систему, зображену на малюнку II.1.

    альт

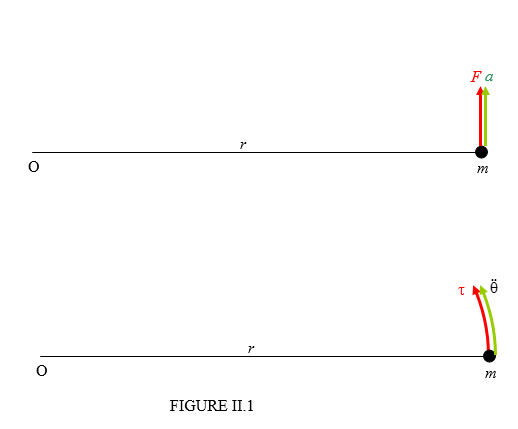
    Частка маси\( m \) прикріплюється легким (тобто нульовим або незначною масою) плечем довжини\( r \) до точки в O , про яку вона може вільно обертати. \( F \)Прикладається сила, і маса, отже, зазнає лінійне\( a = \frac{F}{m} \). прискорення . Кутове прискорення тоді\(\ddot{\Theta} = F.mr \) . Також крутний момент є\(\tau = Fr \) . Тому відношення прикладеного крутного моменту до кутового прискорення є\( mr^{2} \) . Таким чином обертальна інерція є другим моментом інерції. Обертальна інерція і (другий) момент інерції - це одне і те ж, за винятком того, що обертальна інерція - це фізичне поняття, а момент інерції - це його математичне уявлення.