1.4: Криві площини

Плоскі криві, виражені в\( x-y\) координатах

На малюнку I.7 показано, як елементарна довжина\( \delta s \) is related to the corresponding increments in \( x \) and \( y \):

\[ \delta s = \sqrt{\delta x^{2} + \delta y^{2}} = \sqrt{1+\left(\dfrac{dy}{dx}\right)^{2}} \delta x = \sqrt{ \left(\dfrac{dx}{dy}\right)^{2} + 1} \, dy \label{eq:1.4.1} \]

Розглянемо дріт масою на одиницю довжини (лінійна щільність)\( \lambda \) bent into the shape \( y = y(x) \) between \( x = a \) and \( x=b \). The mass of an element \( ds \) is \( \lambda \delta s \) , тому загальна маса дорівнює

\[ \int \lambda \,ds = \int_a^b \lambda \sqrt{1 + \left(\dfrac{dy}{dx}\right)^{2}} \, dx \label{eq:1.4.2} \]

Перші моменти маси про\( y \) - and \( x \) -axes are respectively

\[ \int_a^b \lambda x \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} \, dx \label{eq:1.4.3A} \]

і

\[ \int_a^b \lambda y \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} \, dx \label{eq:1.4.3B} \]

Якщо провід рівномірний і\( \lambda \) is therefore not a function of \( x \) or \( y \), \( \lambda \) can come outside the integral signs in Equations \( \ref{eq:1.4.2}\) - \( \ref{eq:1.4.3B}\), and we hence obtain

\[ \overline{x} = \dfrac{\displaystyle \int_a^b x \sqrt{ 1+\left( \dfrac{dy}{dx} \right)^2} dx } { \displaystyle \int_a^b \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} dx} \label{eq:1.4.4A} \]

і

\[ \overline{y} = \dfrac{\displaystyle \int_a^b y \sqrt{ 1+\left( \dfrac{dy}{dx} \right)^2} dx } { \displaystyle \int_a^b \sqrt{ 1+ \left(\dfrac{dy}{dx}\right)^2} dx} \label{eq:1.4.4B} \]

знаменник у кожному з цих виразів просто є загальною довжиною дроту.

Приклад\(\PageIndex{1}\)

Розглянемо рівномірну дріт, зігнуту в форму півкола.\( x^{2} + y^{2} = a^{2} \), \( x >0 \).

По-перше, можна відзначити, що можна було б очікувати\( \overline{x} > 0.4244a \) (значення для площини напівкруглої ламіни).

Довжина (тобто знаменники в рівняннях\( \ref{eq:1.4.4A}\) and \( \ref{eq:1.4.4B}\)) is just \( \pi a \). Since there are, between \( x \) and \( x + \delta x \), two elemental lengths to account for, one above and one below the \( x \) axis, the numerator of Equation \( \ref{eq:1.4.4A}\) must be

\[2 \int_0^a x \sqrt{1+ \left(\dfrac{dy}{dx}\right)^{2}} dx \nonumber \]

В даному випадку

\[y = \sqrt{a^2 - x^2} \nonumber \]

і

\[ \dfrac{dy}{dx} = \dfrac{-x}{ \sqrt{a^2 - x^2} } \nonumber \]

Перший момент довжини всього півкола

\[\overline{x} = 2 \int_0^a x \sqrt{ 1 + \dfrac{x^2}{a^2-x^2} } dx = 2a \int_0^a \dfrac{x\,dx}{ \sqrt{ a^2-x^2 }} \nonumber \]

З цього моменту студент залишається на свої власні пристрої, щоб вирішити цей інтеграл і вивести\( \overline{x} = \dfrac{2a}{\pi} = 0.6366a \).

Плоскі криві виражені в полярних координатах

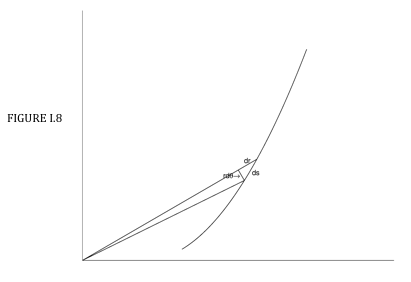
На малюнку I.8 показано, як елементарна довжина\( \delta s \) is related to the corresponding increments in \( r \) and \( \theta \) :

\[ \delta s = \sqrt{( \delta r)^{2} + (r \delta \theta )^{2}} = \sqrt{\left( \dfrac{dr}{d \theta }\right)^{2} + r^{2}} \, \delta \theta = \sqrt{1+\left(r \dfrac{d \theta }{dr}\right)^{2}} \,\delta r. \label{eq:1.4.5} \]

Маса кривої (між\( \theta = a \) і\( \theta = b \) ) дорівнює

\[ \int_ \alpha ^ \beta \lambda \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta. \nonumber \]

Перші моменти про\( y \) - and \( x \) -axes are (recalling that \( x = r \cos \theta \) and \( y = r \sin \theta \) )

\[ \int_ \alpha ^ \beta \lambda r \cos \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta \nonumber \]

і

\[ \int_ \alpha ^ \beta \lambda r \sin \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta. \nonumber \]

Якщо не\( \lambda \) є функцією\( r \) or \( \theta \) , то отримаємо

\[ \overline{x} = \dfrac{1}{L} \int_ \alpha ^ \beta r \cos \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} \, d \theta \label{eq:1.4.6A} \]

і

\[ \overline{y} = \dfrac{1}{L} \int_ \alpha ^ \beta r \sin \theta \sqrt{ \left(\dfrac{dr}{d \theta }\right) ^{2} + r^{2}} d \theta \label{eq:1.4.6B} \]

де e\(L\) - довжина проводу.

Приклад\(\PageIndex{2}\)

Знову розглянемо рівномірну дріт малюнка І.8, зігнуту в форму півкола. Рівняння в полярних координатах просто\( r = a \), and the integration limits are \( \theta = \dfrac{- \pi}{2} \) to \( \theta = \dfrac{+ \pi}{2} \) і довжина є\( \pi a \) .

Таким чином

\[ \overline{x} = \dfrac{1}{ \pi a} \int_{- \pi/2} ^{+ \pi/2} acos \theta [ 0 - a^{2}]^ \frac{1}{2} d \theta = \dfrac{2a}{ \pi } . \nonumber \]

Тепер читач повинен знайти положення центру маси дроту, зігнутого в дугу окружності кута\( 2 \alpha \). The expression obtained should go to \( \dfrac{2 a }{\pi} \), як\( \alpha \)\( \dfrac{\pi}{2} \), and to \( a \) as \( \alpha \) йде до нуля.