1.3: Площині

Плоскі ділянки, в яких рівняння задано в\( x-y \) координатах

У нас крива\( y = y(x) \) (Figure I.3) and we wish to find the position of the centroid of the area under the curve between \( x = a \) and \( x = b \). We consider an elemental slice of width \( \delta x \) на відстані,\( x\) from the \(y \) axis. Its area is \( y \delta x \), і тому загальна площа

\[ A = \int_a^b ydx \label{eq:1.3.1} \]

Перший момент площі зрізу по відношенню до\( y\) axis is \( x y \delta x \), and so the first moment of the entire area is \(\int_a^b xydx\).

Тому

\[ \overline{x} = \frac{ \int_a^b xydyx }{\int_a^b ydyx} = \frac{\int_a^b xydyx}{A} \\label{eq:1.3.2} \]

Бо\( \overline{y} \) ми помічаємо, що відстань центроїда зрізу від \(x \)осі є \( \frac{1}{2}y \), отже, перший момент області про \(x \) вісь є\( \frac{1}{2} y.y \delta x \) .

Тому

\[ \overline{y} = \frac{ \int_a^b y^2dx }{2A} \label{eq:1.3.3} \]

Приклад\(\PageIndex{1}\)

Розглянемо напівкруглу пластинку,\( x^{2} + y^{2} = a^{2} \) , see Figure I.4:

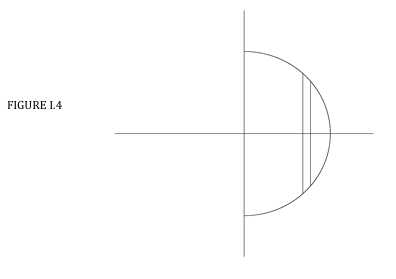
Ми маємо справу з частинами як вище, так\(x \) axis, so the area of the semicircle is \(2\int_0^a ydx\) і нижче і перший момент області є\(2\int_0^a xydx\).

Ви повинні знайти\( \overline{x} = 4a/ (3 \pi) = 0.4244a \).

Тепер розглянемо ламінат\( x^{2} + y^{2} = a^{2} \) , \( y >0 \) (Figure I.5):

Площа елементарного зрізу на цей раз\( y \delta x \) (not \(2 y \delta x \) ), and the integration limits are from \( -a \) to \( +a \). To find \( \overline{y} \), use Equation \( \ref{eq:1.3.3}\), and you should get \( y = 0.4244a \) .

Plane areas in which the equation is given in polar coordinates.

We consider an elemental triangular sector (Figure I.6) between \( \theta \) and \( \theta + \delta \theta \) . The "height" of the triangle is r and the "base" is \( r \delta \theta \). The area of the triangle is \( \frac{1}{2} r^{2} \delta \theta \).

Therefore the whole area =

\[ \frac{1}{2} \int_ \alpha ^ \beta r^{2}d \theta \label{eq:1.3.4} \]

The horizontal distance of the centroid of the elemental sector from the origin (more correctly, from the "pole" of the polar coordinate system) is \( \frac{2}{3} r \cos \theta \) . The first moment of area of the sector with respect to the \(y \) axis is

\( \frac{2}{3}r\cos \theta \times \frac{1}{2} r^{2} \delta \theta = \frac{1}{3}r^{3} \cos \theta \delta \theta \)

so the first moment of area of the entire figure between \( \theta = \alpha \) and \( \theta = \beta \) is

\( \frac{1}{3} \int_ \alpha ^ \beta r^3 \cos \theta d \theta \)

Therefore

\[ \overline{x} = \frac{2 \int_ \alpha ^ \beta r^{3}\cos \theta d \theta }{3\int_ \alpha ^ \beta r^{2} d \theta} \label{eq:1.3.5} \]

Similarly

\[ \overline{x} = \frac{2 \int_ \alpha ^ \beta r^{3}\sin \theta d \theta }{3\int_ \alpha ^ \beta r^{2} d \theta} \label{eq:1.3.6} \]

Example \(\PageIndex{2}\)

Consider the semicircle \( r = a\), \( \theta = \frac{- \pi}{2}\) to \(\frac{+ \pi}{2} \)

\[ \overline{x} = \frac{2a \int_{- \pi /2}^{+ \pi /2} \cos \theta d \theta }{3 \int_{- \pi /2}^{+ \pi /2} d \theta } = \frac{2a}{3 \pi } \int_{- \pi /2}^{+ \pi /2} \cos \theta d \theta = \frac{4a}{3 \pi} \label{eq:1.3.7} \]

The reader should now try to find the position of the centroid of a circular sector (slice of pizza!) of angle \( 2\alpha \) . The integration limits will be \( - \alpha\) to \( + \alpha\).

When you arrive at a formula (which you should keep in a notebook for future reference), check that it goes to \( \frac{4 \alpha}{ 3 \pi} \) if \( \alpha = \frac{ \pi}{2} \), and to \( \frac{2 \pi}{3} \) if \( \alpha = 0\).