Skip to main content
LibreTexts - Ukrayinska

1.2: Площина трикутної пластини

  1. Last updated
  2. Save as PDF
  • Page ID
    76056

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Означення: Медіана трикутника - це лінія від вершини до середини протилежної сторони.

    Теорема I. Три медіани трикутника є одночасними (зустрічаються в одній унікальній точці) у точці, яка становить дві третини відстані від вершини до середини протилежної сторони.

    Теорема II. Центр маси однорідної трикутної пластинки (або центроїда трикутника) знаходиться на зустрічі медіанів.

    Доказ I можна зробити з хорошим векторним аргументом (рис. I.1):

    \(\bf{\text{A}}\)\( \bf{\text{B}}\)Дозволяти , бути вектори\( \text{OA}\) ,\( \text{OB}\) . Потім\( \bf{\text{A+B}}\) йде діагональ паралелограма, з якого\( OA\) і\( \text{OB}\) є дві сторони, і вектор положення точки\( \text{C}_{1}\) is \( \frac{1}{3}(\bf{\text{A+B}})\) .

    Щоб отримати\( \text{C}_{2}\), we see that

    \( {\bf C}_2 = {\bf A} + \dfrac{2}{3}(\text{AM}_2) = {\bf A} + \dfrac{2}{3}({\bf M_2 - A}) = {\bf A} + \dfrac{2}{3}(\dfrac{1}{2}{\bf B- A}) = \dfrac{1}{3}( {\bf A+B})\)

    альт

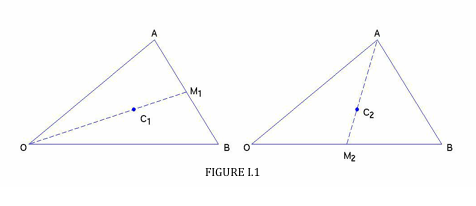
    Таким чином, точки\( \text{C}_{1}\) and \( \text{C}_{2}\) are identical, and the same would be true for the third median, so Theorem I is proved.

    Now consider an elemental slice as in Figure I.2. The centre of mass of the slice is at its mid-point. The same is true of any similar slices parallel to it. Therefore the centre of mass is on the locus of the mid-points - i.e. on a median. Similarly, it is on each of the other medians, and Theorem II is proved.

    alt

    Для цього потрібна була лише певна векторна геометрія. Тепер перейдемо до деякого числення.