24.2: Фізичний маятник

Last updated
Save as PDF

Page ID: 75990

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Фізичний маятник складається з твердого тіла, яке піддається обертанню нерухомої осі навколо нерухомої точки\(S\) (рис. 24.2).

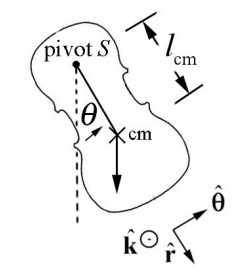
Гравітаційна сила діє в центрі мас фізичного маятника. Позначимо відстань центру мас до точки повороту\(S\) по\(l_{\mathrm{cm}}\). Аналіз крутного моменту майже ідентичний простому маятнику. Крутний момент навколо точки повороту\(S\) задається

\[\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, \mathrm{cm}} \times m \overrightarrow{\mathrm{g}}=l_{\mathrm{cm}} \hat{\mathbf{r}} \times m g(\cos \theta \hat{\mathbf{r}}-\sin \theta \hat{\boldsymbol{\theta}})=-l_{\mathrm{cm}} m g \sin \theta \hat{\mathbf{k}} \nonumber \]

Дотримуючись тих самих кроків, що призвели від Рівняння (24.1.1) до Рівняння (24.1.4), рівняння обертання для фізичного маятника є

\[-m g l_{\mathrm{cm}} \sin \theta=I_{S} \frac{d^{2} \theta}{d t^{2}} \nonumber \]

де\(I_{s}\) момент інерції про точку повороту\(S\). Як і у випадку з простим маятником, для малих кутів\(\sin \theta \approx \theta\), Рівняння (24.2.2) зводиться до простого рівняння гармонічного осцилятора

\[\frac{d^{2} \theta}{d t^{2}} \simeq-\frac{m g l_{\mathrm{cm}}}{I_{S}} \theta \nonumber \]

Рівняння для кута\(\theta(t)\) задається

\[\theta(t)=A \cos \left(\omega_{0} t\right)+B \sin \left(\omega_{0} t\right) \nonumber \]

де кутова частота задається

\[\omega_{0} \simeq \sqrt{\frac{m g l_{\mathrm{cm}}}{I_{S}}} \quad(\text { physical pendulum }) \nonumber \]

і період

\[T=\frac{2 \pi}{\omega_{0}} \simeq 2 \pi \sqrt{\frac{I_{S}}{m g l_{\mathrm{cm}}}} \quad(\text { physical pendulum }) \nonumber \]

Підставити теорему паралельної осі\(I_{S}=m l_{\mathrm{cm}}^{2}+I_{\mathrm{cm}}\) в Рівняння (24.2.6) з результатом, що

\[T \simeq 2 \pi \sqrt{\frac{l_{\mathrm{cm}}}{g}+\frac{I_{\mathrm{cm}}}{m g l_{\mathrm{cm}}}} \quad(\text { physical pendulum }) \nonumber \]

Таким чином, якщо об'єкт «малий» в тому сенсі\(I_{\mathrm{cm}}<<m l_{\mathrm{c}}^{2}\), що, вирази для фізичного маятника зводяться до тих, що для простого маятника. z -складова кутової швидкості задається

\[\omega_{z}(t)=\frac{d \theta}{d t}(t)=-\omega_{0} A \sin \left(\omega_{0} t\right)+\omega_{0} B \cos \left(\omega_{0} t\right) \nonumber \]

Коефіцієнти A і B можуть бути визначені з початкових умов, встановивши t = 0 в Рівняннях (24.2.4) і (24.2.8), в результаті чого утворюються умови, які

\ [\ почати {масив} {l}
A=\ тета (t=0)\ equiv\ theta_ {0}\\
B=\ frac {\ омега_ {z} (t=0)} {\ омега_ {0}}\ equiv\ frac {\ омега_ {z, 0}} {\ omega_ {0}}
\ кінець {масив}\ nonumber\]

Тому рівняння для кута\(\theta(t) \text { and } \omega_{z}(t)=\frac{d \theta}{d t}(t)\) задаються

\ [\ почати {масив} {c}
\ тета (t) =\ theta_ {0}\ cos\ ліворуч (\ омега_ {0} т\ праворуч) +\ frac {\ омега_ {z, 0}} {\ omega_ {0}}\ sin\ ліворуч (\ омега_ {0} т\ праворуч)
\\ омега_ {z} (t) =\ frag c {d\ тета} {d t} (t) =-\ омега_ {0}\ тета_ {0}\ sin\ ліворуч (\ омега_ {0} т\ вправо) +\ омега_ {z, 0}\ cos\ left (\ omega_ {0} t\ праворуч)
\ end {масив}\ nonumber\]