15.5: Опрацьовані приклади

Приклад 15.1 Пружне одновимірне зіткнення між двома об'єктами

Малюнок 15.7 Пружне зіткнення між двома неоднаковими візками

Розглянемо пружне зіткнення двох візків уздовж колії; інцидентний візок 1 має масу\(m_{1}\ and moves with initial speed \(v_{1,i}\). Цільова візок має масу\(m_{2}=2 m_{1}\) і спочатку знаходиться в стані спокою\(v_{2, i}=0\),, (рис. 15.7). Відразу після зіткнення візок, що інцидент має кінцеву швидкість,\(v_{1, f}\) а цільовий візок має кінцеву швидкість\(v_{2, f}\). Обчисліть кінцеву х-складову швидкостей візків в залежності від початкової швидкості\(v_{1, i}\).

Рішення: Схема руху імпульсу для об'єктів до (початковий стан) та після (кінцевий стан) зіткнення показана на малюнку 15.7. Ми можемо негайно використовувати наші результати вище за допомогою\(m_{2}=2 m_{1}\) і\(v_{2, i}=0\). Кінцева x -складова швидкості візка 1 задається рівнянням (15.3.14), де ми використовуємо\(v_{1 x, i}=v_{1, i}\).

\[v_{1 x, f}=-\frac{1}{3} v_{1, i} \nonumber \]Кінцева x-складова швидкості візка 2 задається рівнянням (15.4.17)\[v_{2 x, f}=\frac{2}{3} v_{1, i} \nonumber \]

Приклад 15.2 Розсіювання кінетичної енергії при абсолютно нееластичному зіткненні двох об'єктів

Малюнок 15.7b Нееластичне зіткнення між двома неоднаковими візками

Падаючий візок маси\(m_{1}\) і початкової швидкості\(v_{1,i}\) стикається абсолютно непружно з візком маси\(m_{2}\), яка спочатку знаходиться в стані спокою (рис. 15.7б). Зовнішні сили, що діють на об'єкти в напрямку зіткнення, відсутні. Знайти\(\Delta K / K_{\text {initial }}=\left(K_{\text {final }}-K_{\text {initial }}\right) / K_{\text {initial }}\)

Рішення: За відсутності будь-якої чистої сили на системі, що складається з двох візків, імпульс після зіткнення буде таким же, як і до зіткнення. Після зіткнення візки рухатимуться у напрямку початкової швидкості падаючого візка із загальною швидкістю,\(v_{f}\) знайденою при застосуванні умови імпульсу

\[m_{1} v_{1, i}=\left(m_{1}+m_{2}\right) v_{f} \Rightarrow v_{f}=\frac{m_{1}}{m_{1}+m_{2}} v_{1, i} \nonumber \]Початкова відносна швидкість дорівнює\(v_{i}^{\mathrm{rel}}=v_{1, i}\). Кінцева відносна швидкість дорівнює нулю, оскільки візки злипаються разом, тому, використовуючи Рівняння (15.3.26), зміна кінетичної енергії є\[\Delta K=-\frac{1}{2} \mu\left(v_{i}^{r e l}\right)^{2}=-\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{1, i}^{2} \nonumber \] Відношення зміни кінетичної енергії до початкової кінетичної енергії тоді\[\Delta K / K_{\text {initial}}=-\frac{m_{2}}{m_{1}+m_{2}} \nonumber \] Як перевірка, ми можемо обчислити зміну кінетичної енергії за допомогою\[\Delta K=\left(K_{f}-K_{i}\right)=\frac{1}{2}\left(m_{1}+m_{2}\right) v_{f}^{2}-\frac{1}{2} v_{1, i}^{2} =\frac{1}{2}\left(m_{1}+m_{2}\right)\left(\frac{m_{1}}{m_{1}+m_{2}}\right)^{2} v_{1, i}^{2}-\frac{1}{2} v_{1, i}^{2} =\left(\frac{m_{1}}{m_{1}+m_{2}}-1\right)\left(\frac{1}{2} m_{1} v_{1, i}^{2}\right)=-\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{1, i}^{2} \nonumber \]

відповідно до Рівняння (15.4.4).

Приклад 15.3 Підстрибуючі суперкулі

Малюнок 15.8b Два суперкулі падіння

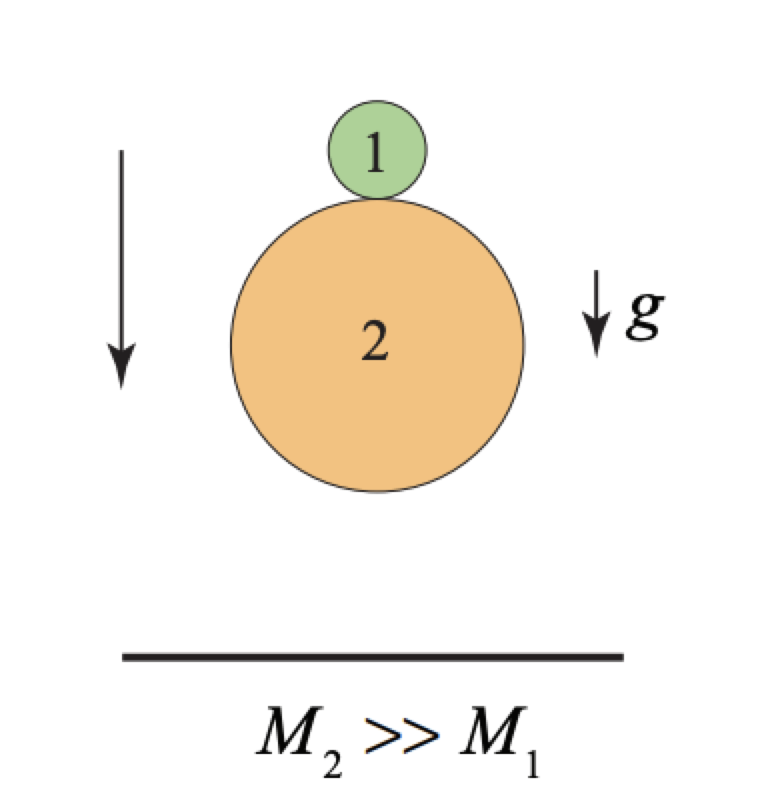
Розглянемо дві кулі, які скидаються з висоти\(h_{i}\) над землею, один на інший (рис. 15.8). Куля 1 знаходиться зверху і має масу\(M_{1}\), а кулька 2 знаходиться під ним і має масу\(M_{2}\) с\(M_{2}>>M_{1}\). Припустимо, що немає втрат кінетичної енергії під час всіх зіткнень. М'яч 2 спочатку стикається з землею і підбиває. Потім, коли куля 2 починає рухатися вгору, він стикається з м'ячем 1, який все ще рухається вниз (малюнок внизу зліва). Наскільки високо буде м'яч 1 відскок в повітрі? Підказка: розгляньте це зіткнення, яке бачить спостерігач, що рухається вгору з тією ж швидкістю, що і м'яч 2 після зіткнення з землею. Яку швидкість має куля 1 в цій опорній рамці після того, як він зіткнеться з м'ячем 2?

Рішення

Система складається з двох куль і землі. Існує п'ять спеціальних станів для цього руху, показаних на малюнку нижче.

частина а)

Початковий стан: кульки звільняються від спокою на висоті\(h_{i}\) над землею.

Стан A: кулі просто досягають землі зі швидкістю\(v_{a}=\sqrt{2 g h_{i}}\). Це випливає з\(\Delta E_{\text {mесh}}=0 \Rightarrow \Delta K=-\Delta U\). Таким чином\((1 / 2) m v_{a}^{2}-0=-m g \Delta h=m g h_{i} \Rightarrow v_{a}=\sqrt{2 g h_{i}}\)

Стан Б: безпосередньо перед зіткненням куль. Куля 2 зіткнувся з землею і змінив напрямок з тією ж швидкістю,\(v_{a}\) але куля 1 все ще рухається вниз зі швидкістю\(v_{a}\).

Стан C: відразу після зіткнення кульок. Тому що ми припускаємо, що\(m_{2} \gg m_{1}\) куля 2 не змінює свою швидкість в результаті зіткнення, тому він все ще рухається 2 вгору зі швидкістю\(v_{a}\). В результаті зіткнення куля 1 переміщається вгору зі швидкістю\(v_{b}\)

Кінцевий стан: м'яч 1 досягає максимальної висоти\(h_{f}=v_{b}^{2} / 2 g\) над землею. Це знову випливає з\(\Delta K=-\Delta U \Rightarrow 0-(1 / 2) m v_{b}^{2}=-m g \Delta h=-m g h_{f} \Rightarrow h_{f}=v_{b}^{2} / 2 g\)

Вибір опорного кадру:

Як зазначено в підказці вище, це зіткнення найкраще аналізувати з опорної рамки спостерігача, що рухається вгору\(v_{a}\) зі швидкістю кулі 2 відразу після того, як він відскочив із землею. У цьому кадрі безпосередньо, перед зіткненням, куля 1 рухається вниз зі швидкістю,\(v_{b}^{\prime}\) яка вдвічі перевищує швидкість, яку бачить спостерігач у стані спокою на землі (лабораторний контрольний кадр). \[v_{a}^{\prime}=2 v_{a} \nonumber \]

Маса кулі 2 набагато більше, ніж маса кулі 1,\(m_{2} \gg m_{1}\) Це дозволяє нам вважати зіткнення (між державами B і C) бути еквівалентним м'яч 1 відскакує від жорсткої стіни, в той час як м'яч 2 відчуває практично ніякої віддачі. Отже, куля 2 залишається в стані спокою в опорній рамці, рухаючись вгору\(\mathcal{V}_{a}\) зі швидкістю по відношенню до спостерігача в стані спокою на землі. Перед зіткненням куля 1 має швидкість\(v_{a}^{\prime}=2 v_{a}\) Оскільки під час зіткнення немає втрати кінетичної енергії, результатом зіткнення є те, що куля 1 змінює напрямок, але підтримує однакову швидкість,\[v_{b}^{\prime}=2 v_{a} \nonumber \] Однак, за словами спостерігача в стані спокою на землі, після зіткнення м'яч 1 рухається вгору зі швидкістю\[v_{b}=2 v_{a}+v_{a}=3 v_{a} \nonumber \] Під час відскоку механічна енергія меншого суперкулі є постійною (ми розглядаємо менший суперкуля і Землю як систему), отже, між станом C і кінцевим станом,\[\Delta K+\Delta U=0 \nonumber \] Зміна кінетичної енергії є\[\Delta K=-\frac{1}{2} m_{1}\left(3 v_{a}\right)^{2} \nonumber \] Зміна потенційної енергії є\[\Delta U=m_{1} g h_{f} \nonumber \] Отже, умова, що механічна енергія є постійною (Рівняння (15.5.10)) тепер\[-\frac{1}{2} m_{1}\left(3 v_{1 a}\right)^{2}+m_{1} g h_{f}=0 \nonumber \] Ми можемо переписати рівняння (15.5.13) як\[m_{1} g h_{f}=9 \frac{1}{2} m_{1}\left(v_{a}\right)^{2} \nonumber \] Нагадаємо, що ми також можемо використовувати той факт, що механічна енергія не змінюється між початковим станом та станом А, отримуючи рівняння, подібне рівнянню (15.5.14), \[m_{1} g h_{i}=\frac{1}{2} m_{1}\left(v_{a}\right)^{2} \nonumber \]Тепер підставляємо вираз для кінетичної енергії в Рівнянні (15.5.15) на Рівняння (15.5.14), що дає\[m_{1} g h_{f}=9 m_{1} g h_{i} \nonumber \] Таким чином куля 1 досягає максимальної висоти\[h_{f}=9 h_{i} \nonumber \]