15.7: Двовимірні зіткнення в опорному кадрі центру маси

Двовимірне зіткнення в опорному кадрі центру маси

Розглянемо пружне зіткнення двох частинок в лабораторній системі відліку (рис. 15.9). Частинка 1 маси\(m_{1}\) спочатку рухається зі швидкістю\(\overrightarrow{\mathbf{v}}_{1, i}\) і пружно стикається з частинкою 2 маси\(m_{2}\), яка спочатку знаходиться в стані спокою. Після зіткнення частка 1 рухається зі швидкістю\(\overrightarrow{\mathbf{v}}_{1, f}\) і частка 2 рухається зі швидкістю\(\overrightarrow{\mathbf{v}}_{2, f}\). У розділі 15.7.1 ми визначили\(v_{1, f}\), як знайти\(v_{2, f}\), і з\(\theta_{2, f}\) точки зору\(v_{1, i}\) і\(\theta_{2, f}\). Тепер ми проаналізуємо зіткнення в системі відліку центру маси, яка посилюється з лабораторного кадру швидкістю центру маси, заданої\[\overrightarrow{\mathbf{v}}_{c m}=\frac{m_{1} \overrightarrow{\mathbf{v}}_{1, i}}{m_{1}+m_{2}} \nonumber \]

Оскільки ми припускали, що на систему не діють зовнішні сили, швидкість центру маси залишається постійною під час взаємодії.

Малюнок 15.13 Двовимірне пружне зіткнення в системі відліку центру маси

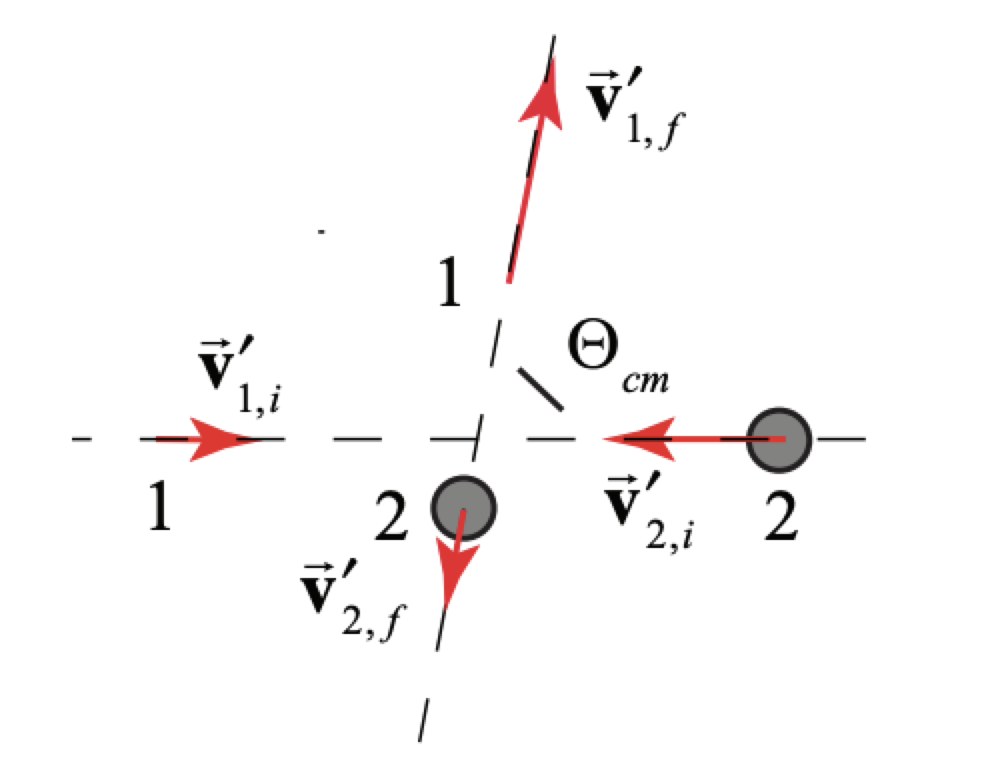
Нагадаємо, швидкості частинок 1 і 2 в рамці центру маси задаються (Рівняння, (15.2.9) і (15.2.10)). У системі відліку центру маси швидкості двох вхідних частинок знаходяться в протилежних напрямках, як і швидкості двох вихідних частинок після зіткнення (рис. 15.13). Кут\(\Theta_{c m}\) між вхідною і вихідною швидкостями називається кутом розсіювання центру маси.

Розсіювання в опорному кадрі центру маси

Розглянемо зіткнення між частинкою 1 маси\(m_{1}\) і швидкості\(\overrightarrow{\mathbf{v}}_{1, i}\) і частинкою 2 маси\(m_{2}\) в стані спокою в лабораторному кадрі. Частинка 1 розсіюється пружно через кут розсіювання\(\Theta\) в рамці центру маси. Швидкість центру маси задається за допомогою\[\overrightarrow{\mathbf{v}}_{c m}=\frac{m_{1} \overrightarrow{\mathbf{v}}_{1, i}}{m_{1}+m_{2}} \nonumber \]

У рамці центру маси імпульс системи двох частинок дорівнює нулю\[\overrightarrow{\mathbf{0}}=m_{1} \overrightarrow{\mathbf{v}}_{1, i}^{\prime}+m_{2} \overrightarrow{\mathbf{v}}_{2, i}^{\prime}=m_{1} \overrightarrow{\mathbf{v}}_{1, f}^{\prime}+m_{2} \overrightarrow{\mathbf{v}}_{2, f}^{\prime} \nonumber \] Тому\[\overrightarrow{\mathbf{v}}_{1, i}^{\prime}=-\frac{m_{2}}{m_{1}} \overrightarrow{\mathbf{v}}_{2, i}^{\prime} \nonumber \]\[\overrightarrow{\mathbf{v}}_{1, f}^{\prime}=-\frac{m_{2}}{m_{1}} \overrightarrow{\mathbf{v}}_{2, f}^{\prime} \nonumber \] енергетична умова в кадрі центру маси - це\[\frac{1}{2} m_{1} v_{1, i}^{\prime 2}+\frac{1}{2} m_{2} v_{2, i}^{\prime 2}=\frac{1}{2} m_{1} v_{1, f}^{\prime 2}+\frac{1}{2} m_{2} v_{2, f}^{\prime 2} \nonumber \] заміщення рівнянь (15.7.4) та (15.7.5) на Рівняння (15.7.6) дає\[v_{1, i}^{\prime}=v_{1, f}^{\prime} \nonumber \] (ми розглядаємо лише величини) . Тому\[v_{2, i}^{\prime}=v_{2, f}^{\prime} \nonumber \] Оскільки величина швидкості частинки в системі відліку центру маси пропорційна відносній швидкості двох частинок, рівняння (15.7.7) та (15.7.8) означають, що величина відносної швидкості також не змінюється,\[\left|\overrightarrow{\mathbf{v}}_{1,2, i}^{\prime}\right|=\left|\overrightarrow{\mathbf{v}}_{1,2, f}^{\prime}\right| \nonumber \] перевіряючи наші раніше результат, що для пружного зіткнення відносна швидкість залишається незмінною, (Рівняння (15.2.20)). Однак напрямок відносної швидкості обертається кутом розсіювання центру маси\(\Theta_{c m}\). Це узагальнює принцип енергії-імпульсу до двох вимірів. Нагадаємо, що відносна швидкість не залежить від системи відліку,\[\overrightarrow{\mathbf{v}}_{1, i}-\overrightarrow{\mathbf{v}}_{2, i}=\overrightarrow{\mathbf{v}}_{1, i}^{\prime}-\overrightarrow{\mathbf{v}}_{2, i}^{\prime} \nonumber \] в лабораторній системі відліку, отже\(\overrightarrow{\mathbf{v}}_{1,2, i}^{\prime}=\overrightarrow{\mathbf{v}}_{1,2, i}=\overrightarrow{\mathbf{v}}_{1, i}\), початкова відносна швидкість є, а швидкості в центрі маси кадру частинок тоді і\[\overrightarrow{\mathbf{V}}_{1, i}^{\prime}=\frac{\mu}{m_{1}} \overrightarrow{\mathbf{v}}_{1, i} \nonumber \]\[\overrightarrow{\mathbf{v}}_{2, i}^{\prime}=-\frac{\mu}{m_{2}} \overrightarrow{\mathbf{v}}_{1, i} \nonumber \] тому величини\(\overrightarrow{\mathbf{v}}_{2, i}=\overrightarrow{\mathbf{0}}\) кінцеві швидкості в рамці центру маси є\[v_{1, f}^{\prime}=v_{1, i}^{\prime}=\frac{\mu}{m_{1}} v_{1,2, i}^{\prime}=\frac{\mu}{m_{1}} v_{1,2, i}=\frac{\mu}{m_{1}} v_{1, i} \nonumber \]\[v_{2, f}^{\prime}=v_{2, i}^{\prime}=\frac{\mu}{m_{2}} v_{1,2, i}^{\prime}=\frac{\mu}{m_{2}} v_{1,2, i}=\frac{\mu}{m_{2}} v_{1, i} \nonumber \]

Приклад 15.8 Розсіювання у кадрах Lab та CM

Частинка 1 маси\(m_{1}\) і швидкості\(\overrightarrow{\mathbf{v}}_{1, i}\) частинкою маси\(m_{2}\) в спокої в лабораторному кадрі розсіюється пружно через кут розсіювання\(\Theta\) в центрі рамки маси (рис. 15.14). Знайти (i) кут розсіювання вхідної частинки в лабораторному кадрі, (ii) величину кінцевої швидкості вхідної частинки в лабораторній системі відліку і (iii) дробові втрати кінетичної енергії вхідної частинки.

Малюнок 15.14 Розсіювання в лабораторних і центральних системах відліку

Рішення

i) Для визначення кута розсіювання центру маси ми використовуємо закон трансформації швидкостей\[\overrightarrow{\mathbf{v}}_{1, f}^{\prime}=\overrightarrow{\mathbf{v}}_{1, f}-\overrightarrow{\mathbf{v}}_{c m} \nonumber \]. На малюнку 15.15 ми показуємо зіткнення в рамці центру мас разом з кінцевими швидкостями лабораторного кадру і кутами розсіювання.

Малюнок 15.15 Кінцеві швидкості стикаються частинок

Векторне розкладання рівняння (15.7.15) дає,\[v_{1, f} \cos \theta_{1, i}=v_{1, f}^{\prime} \cos \Theta_{c m}-v_{c m} \nonumber \]\[v_{1, f} \sin \theta_{1, i}=v_{1, f}^{\prime} \sin \Theta_{c m} \nonumber \] де ми обираємо як наші напрямки горизонтальне та вертикальне рівняння ділення (15.7.17) на (15.7.16)\(v_{1, i}^{\prime}=v_{1, f}^{\prime}\),\[\tan \theta_{1, i}=\frac{v_{1, f} \sin \theta_{1, i}}{v_{1, f} \cos \theta_{1, i}}=\frac{v_{1, f}^{\prime} \sin \Theta_{c m}}{v_{1, f}^{\prime} \cos \Theta_{c m}-v_{c m}} \nonumber \] оскільки ми можемо переписати рівняння (15.7.18) як\[\tan \theta_{1, i}=\frac{v_{1, i}^{\prime} \sin \Theta_{c m}}{v_{1, i}^{\prime} \cos \Theta_{c m}-v_{c m}} \nonumber \]

Тепер підставляємо рівняння (15.7.12) і\(v_{c m}=m_{1} v_{1, i} /\left(m_{1}+m_{2}\right)\) в Рівняння (15.7.19), що дає\[\tan \theta_{1, i}=\frac{m_{2} \sin \Theta_{c m}}{\cos \Theta_{c m}-m_{1} / m_{2}} \nonumber \] Таким чином, в лабораторному кадрі частинка 1 розсіюється на кут\[\theta_{1, i}=\tan ^{-1}\left(\frac{m_{2} \sin \Theta_{c m}}{\cos \Theta_{c m}-m_{1} / m_{2}}\right) \nonumber \]

ii) Ми можемо обчислити квадрат кінцевої швидкості в лабораторному кадрі\[\overrightarrow{\mathbf{v}}_{1, f} \cdot \overrightarrow{\mathbf{v}}_{1, f}=\left(\overrightarrow{\mathbf{v}}_{1, f}^{\prime}+\overrightarrow{\mathbf{v}}_{c m}\right) \cdot\left(\overrightarrow{\mathbf{v}}_{1, f}^{\prime}+\overrightarrow{\mathbf{v}}_{c m}\right) \nonumber \], який стає\[v_{1, f}^{2}=v_{1, f}^{\prime 2}+2 \overrightarrow{\mathbf{v}}_{1, f}^{\prime} \cdot \overrightarrow{\mathbf{v}}_{c m}+v_{c m}^{2}=v_{1, f}^{\prime 2}+2 v_{1, f}^{\prime} v_{c m} \cos \Theta_{c m}+v_{c m}^{2} \nonumber \]

Використовуємо той факт, що\(v_{1, f}^{\prime}=v_{1, i}^{\prime}=\left(\mu / m_{1}\right) v_{1,2, i}=\left(\mu / m_{1}\right) v_{1, i}=\left(m_{2} / m_{1}+m_{2}\right) v_{1, i}\) переписати рівняння (15.7.23) як\[v_{1, f}^{2}=\left(\frac{m_{2}}{m_{1}+m_{2}}\right)^{2} v_{1, i}^{2}+2 \frac{m_{2} m_{1}}{\left(m_{1}+m_{2}\right)^{2}} v_{1, i} \cos \Theta_{c m}+\frac{m_{1}^{2}}{\left(m_{1}+m_{2}\right)^{2}} v_{1, i}^{2} \nonumber \] This\[v_{1, f}=\frac{\left(m_{2}^{2}+2 m_{2} m_{1} \cos \Theta_{c m}+m_{1}^{2}\right)^{1 / 2}}{m_{1}+m_{2}} v_{1, i} \nonumber \]

(iii) Дробова зміна кінетичної енергії частинки 1 в лабораторному кадрі задається\[\frac{K_{1, f}-K_{1, i}}{K_{1, i}}=\frac{v_{1, f}^{2}-v_{1, i}^{2}}{v_{1, i}^{2}}=\frac{m_{2}^{2}+2 m_{2} m_{1} \cos \Theta_{c m}+m_{1}^{2}}{\left(m_{1}+m_{2}\right)^{2}}-1=\frac{2 m_{2} m_{1}\left(\cos \Theta_{c m}-1\right)}{\left(m_{1}+m_{2}\right)^{2}} \nonumber \] ми також можемо визначити кут розсіювання\(\Theta_{c m}\) в системі відліку центру маси від кута\(\theta_{1, i}\) розсіювання частинки 1 в лабораторії. Тепер ми перепишемо відносини імпульсу як\[v_{1, f} \cos \theta_{1, i}+v_{c m}=v_{1, f}^{\prime} \cos \Theta_{c m} \nonumber \]\[v_{1, f} \sin \theta_{1, i}=v_{1, f}^{\prime} \sin \Theta_{c m} \nonumber \]

Подібно до вищезгаданого аргументу, ми маємо, що\[\tan \Theta_{c m}=\frac{v_{1, f} \sin \theta_{1, f}}{v_{1, f} \cos \theta_{1, f}+v_{c m}} \nonumber \] Нагадаємо з нашого аналізу зіткнення в лабораторному кадрі, що якщо ми вкажемо один з чотирьох параметрів\(v_{1, f}, v_{2, f}, \theta_{1, f}\) або\(v_{1, f}\) тоді ми можемо вирішити для інших трьох з точки зору початкових параметрів\(v_{1, i}\) і\(v_{2, i}\). З цим застереженням ми можемо використовувати рівняння (15.7.29) для визначення\(\Theta_{c m}\)