14.4: Зміна потенційної енергії та нульової точки для потенційної енергії

Ми вже розрахували роботу, виконану різними консервативними силами: постійною гравітацією біля поверхні землі, силою пружини та всесвітньою силою тяжіння. Ми вибирали систему в кожному випадку так, щоб консервативна сила була зовнішньою силою. У кожному конкретному випадку зміни потенційної енергії не відбувалося і виконана робота дорівнювала зміні кінетичної енергії,

\[W_{\mathrm{ext}}=\Delta K_{\mathrm{sys}} \nonumber \]

Ми зараз ставимося до кожної з цих консервативних сил як до внутрішніх сил і розраховуємо зміну потенційної енергії системи за нашим визначенням.

\[\Delta U_{\mathrm{sys}}=-W_{\mathrm{c}}=-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{\mathrm{c}} \cdot d \overrightarrow{\mathbf{r}} \nonumber \]

Ми також виберемо нульовий опорний потенціал для потенційної енергії системи, щоб ми могли розглянути всі зміни потенційної енергії щодо цього опорного потенціалу.

Зміна гравітаційної потенційної енергії поблизу поверхні Землі

Розглянемо на прикладі об'єкта, що падає біля поверхні землі. Вибираємо нашу систему, яка складається з землі та об'єкта. Гравітаційна сила тепер є внутрішньою консервативною силою, що діє всередині системи. Відстань, що розділяє об'єкт і центр мас землі, і швидкості землі і об'єкта задає початковий і кінцевий стани.

Давайте виберемо систему координат з початком на поверхні землі і + y - напрямком, спрямованим від центру землі. Оскільки зміщення землі мізерно мало, нам потрібно лише розглянути зміщення об'єкта, щоб обчислити зміну потенційної енергії системи.

Припустимо, що об'єкт починається на початковій висоті\(y_{i}\) над поверхнею землі і закінчується на кінцевій висоті\(y_{f}\). Гравітаційна сила на об'єкт задається\(\overrightarrow{\mathbf{F}}^{g}=-m g \hat{\mathbf{j}}\), зміщення задається\(d \overrightarrow{\mathbf{r}}=d y \hat{\mathbf{j}}\), а скалярний твір задається\(\overrightarrow{\mathbf{F}}^{g} \cdot d \overrightarrow{\mathbf{r}}=-m g \hat{\mathbf{j}} \cdot d y \hat{\mathbf{j}}=-m g d y\). Потім робота, виконана гравітаційною силою на об'єкті

\[W^{g}=\int_{y_{i}}^{y_{f}} \overrightarrow{\mathbf{F}}^{g} \cdot d \overrightarrow{\mathbf{r}}=\int_{y_{i}}^{y_{f}}-m g d y=-m g\left(y_{f}-y_{i}\right) \nonumber \]

Зміна потенційної енергії потім задається

\[\Delta U^{g}=-W^{g}=m g \Delta y=m g y_{f}-m g y_{i} \nonumber \]

Вводимо потенційну енергетичну функцію U так, щоб

\[\Delta U^{g} \equiv U_{f}^{g}-U_{i}^{g} \nonumber \]

Тільки відмінності в функції\(U^{g}\) мають фізичний сенс. Ми можемо вибрати нульову опорну точку для потенційної енергії де завгодно. Ми маємо певну гнучкість, щоб адаптувати наш вибір нуля для потенційної енергії, щоб найкращим чином відповідати певній проблемі. Тому що зміна потенційної енергії залежало лише від зміщення,\(\Delta y\). У наведеному вище виразі для зміни потенційної енергії (Рівняння (14.4.4)), нехай\(y_{f}=y\) буде довільна точка і\(y_{i}=0\) позначимо поверхню землі. Виберіть нульовий опорний потенціал для потенційної енергії, яка буде знаходитися на поверхні землі, що відповідає нашому\(y=0\) походженню, с\(U^{g}(0)=0\). Тоді

\[\Delta U^{g}=U^{g}(y)-U^{g}(0)=U^{g}(y) \nonumber \]

\(y_{i}=0, y_{f}=y\)Заставте і рівняння (14.4.6) у Рівняння (14.4.4), що дає потенційну енергію як функцію висоти y над поверхнею землі,

\[U^{g}(y)=m g y, \text { with } U^{g}(y=0)=0 \nonumber \]

Закон Гука Весна-об'єктна система

Розглянемо пружинно-предметну систему, що лежить на горизонтальній поверхні без тертя, причому одним кінцем пружини закріплюється на стіні, а іншим кінцем прикріплена до об'єкта масою m (рис. 14.7). Сила пружини - внутрішня консервативна сила. Стіна надає зовнішню силу на систему пружинних предметів, але оскільки точка зіткнення стіни з пружиною не піддається зміщенню, ця зовнішня сила не діє.

Малюнок 14.7 Система пружинних об'єктів.

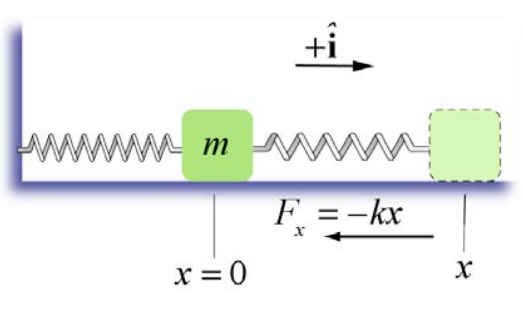
Виберіть початок в положенні центру предмета, коли пружина розслаблена (положення рівноваги). Дозволяти x - зміщення об'єкта від початку. Ми вибираємо\(+\hat{\mathbf{i}}\) одиничний вектор, щоб вказувати в напрямку руху об'єкта при розтягуванні пружини (праворуч від x = 0 на малюнку). Потім зусилля пружини на масу задається\(\overrightarrow{\mathbf{F}}^{s}=F_{x}^{s} \hat{\mathbf{i}}=-k x \hat{\mathbf{i}}\). Зсув є\(d \overrightarrow{\mathbf{r}}=d x \hat{\mathbf{i}}\). Скалярний добуток є\(\overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=-k x \hat{\mathbf{i}} \cdot d x \hat{\mathbf{i}}=-k x d x\). Робота, виконана силою пружини на масу, становить

\[W^{s}=\int_{x=x_{i}}^{x=x_{f}} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=-\frac{1}{2} \int_{x=x_{i}}^{x=x_{f}}-\frac{1}{2}(-k x) d x=-\frac{1}{2} k\left(x_{f}^{2}-x_{i}^{2}\right) \nonumber \]

Потім ми визначаємо зміну потенційної енергії в системі пружинних об'єктів при переміщенні об'єкта з початкового положення\(x_{i}\) з рівноваги в кінцеве положення\(x_{f}\) від рівноваги шляхом

\[\Delta U^{\mathrm{s}} \equiv U^{\mathrm{s}}\left(x_{f}\right)-U^{\mathrm{s}}\left(x_{i}\right)=-W^{\mathrm{s}}=\frac{1}{2} k\left(x_{f}^{2}-x_{i}^{2}\right) \nonumber \]

Тому довільне розтягування або стиснення системи пружинних об'єктів від рівноваги\(x_{i}=0\) до кінцевого положення\(x_{f}=x\) змінює потенційну енергію на

\[\Delta U^{\mathrm{s}}=U^{\mathrm{s}}\left(x_{f}\right)-U^{\mathrm{s}}(0)=\frac{1}{2} k x^{2} \nonumber \]

Для системи пружинних об'єктів існує очевидний вибір положення, де потенційна енергія дорівнює нулю, положення рівноваги пружинного об'єкта,

\[U^{\mathrm{s}}(0) \equiv 0 \nonumber \]

Тоді при такому виборі нульового опорного потенціалу потенційна енергія як функція зсуву х з положення рівноваги задається

\[U^{s}(x)=\frac{1}{2} k x^{2}, \text { with } U^{s}(0) \equiv 0 \nonumber \]

Зворотна квадратна сила тяжіння

Розглянемо систему, що складається з двох об'єктів мас\(m_{1}\) і\(m_{2}\) які розділені між центром до центру відстані\(r_{2, 1}\). Система координат показана на малюнку 14.8. Внутрішня гравітаційна сила на об'єкт 1, обумовлена взаємодією між двома об'єктами, задається

\[\overrightarrow{\mathbf{F}}_{2,1}^{G}=-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} \hat{\mathbf{r}}_{2,1} \nonumber \]

Вектор зміщення задається за допомогою\(d \overrightarrow{\mathbf{r}}_{2,1}=d r_{2,1} \hat{\mathbf{r}}_{2,1}\). Отже, скалярний добуток

\[\overrightarrow{\mathbf{F}}_{2,1}^{G} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} \hat{\mathbf{r}}_{2,1} \cdot d r_{2,1} \hat{\mathbf{r}}_{2,1}=-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} d r_{2,1} \nonumber \]

Малюнок 14.8 Гравітаційна взаємодія

Використовуючи наше визначення потенційної енергії (Рівняння (14.3.4)), ми маємо, що зміна гравітаційної потенційної енергії системи при переміщенні двох об'єктів з початкового положення, в якому центр маси двох об'єктів є\(r_{i}\) відстані один від одного до кінцевого положення, в якому центр маса двох об'єктів відстань\(r_{f}\) один від одного задається

\[\Delta U^{G}=-\int_{A}^{B} \overrightarrow{\mathbf{F}}_{2,1}^{G} \cdot d \overrightarrow{\mathbf{r}}_{2,1}=-\int_{r_{i}}^{f}-\frac{G m_{1} m_{2}}{r_{2,1}^{2}} d r_{2,1}=-\left.\frac{G m_{1} m_{2}}{r_{2,1}}\right|_{r_{i}} ^{r_{f}}=-\frac{G m_{1} m_{2}}{r_{f}}+\frac{G m_{1} m_{2}}{r_{i}} \nonumber \]

Тепер ми вибираємо нашу точку відліку, щоб нуль потенційної енергії був на нескінченності,\(r_{i}=\infty\) з вибором, що\(U^{G}(\infty) \equiv 0\). Роблячи цей вибір, термін\(1 / r\) у виразі i для зміни потенційної енергії зникає, коли\(r_{i}=\infty\). Гравітаційна потенційна енергія як функція відносної відстані r між двома об'єктами задається

\[U^{G}(r)=-\frac{G m_{1} m_{2}}{r}, \text { with } U^{G}(\infty) \equiv 0 \nonumber \]